Introduction to Statistics for the Social Sciences SBS

Introduction to Statistics for the Social Sciences SBS 200, COMM 200, GEOG 200, PA 200, POL 200, or SOC 200 Lecture Section 001, Fall 2015 Room 150 Harvill Building 10: 00 - 10: 50 Mondays, Wednesdays & Fridays. http: //courses. eller. arizona. edu/mgmt/delaney/d 15 s_database_weekone_screenshot. xlsx

By the end of lecture today 10/28/15 Logic of hypothesis testing Steps for hypothesis testing Levels of significance (Levels of alpha) what does p < 0. 05 mean? what does p < 0. 01 mean? One-sample z-tests and t-tests

Before next exam (November 20 th) Please read chapters 1 - 11 in Open. Stax textbook Please read Chapters 2, 3, and 4 in Plous Chapter 2: Cognitive Dissonance Chapter 3: Memory and Hindsight Bias Chapter 4: Context Dependence

Homework Assignment Worksheet Assignment 16 One-sample z and t hypothesis tests Due: Friday, October 30 th

Everyone will want to be enrolled in one of the lab sessions Labs continue this week

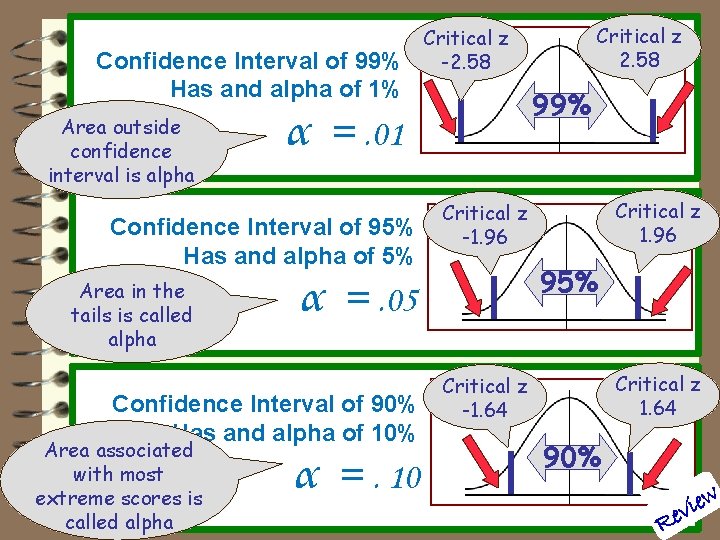
Confidence Interval of 99% Has and alpha of 1% Area outside confidence interval is alpha Area in the tails is called alpha α =. 10 Critical z 1. 96 Critical z -1. 96 95% α =. 05 Confidence Interval of 90% Has and alpha of 10% Area associated with most extreme scores is called alpha 99% α =. 01 Confidence Interval of 95% Has and alpha of 5% Critical z 2. 58 Critical z -2. 58 Critical z 1. 64 Critical z -1. 64 90% ew i v Re

Rejecting the null hypothesis The result is “statistically significant” if: • the observed statistic is larger than the critical statistic (which can be a ‘z” or “t” or “r” or “F” or x 2) observed stat > critical stat If we want to reject the null, we want our t (or z or r or F or x 2) to be big • the p value is less than 0. 05 (which is our alpha) p < 0. 05 If we want to reject the null, we want our “p” to be small!! • we reject the null hypothesis • then we have support for our alternative hypothesis ew i v Re

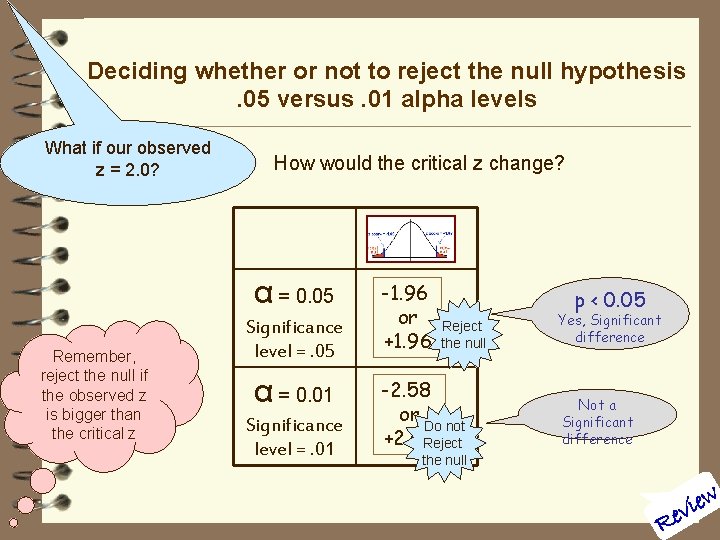
Deciding whether or not to reject the null hypothesis. 05 versus. 01 alpha levels What if our observed z = 2. 0? How would the critical z change? α = 0. 05 Remember, reject the null if the observed z is bigger than the critical z Significance level =. 05 α = 0. 01 Significance level =. 01 -1. 96 or +1. 96 p < 0. 05 Reject the null -2. 58 or Do not +2. 58 Reject Yes, Significant difference Not a Significant difference the null ew i v Re

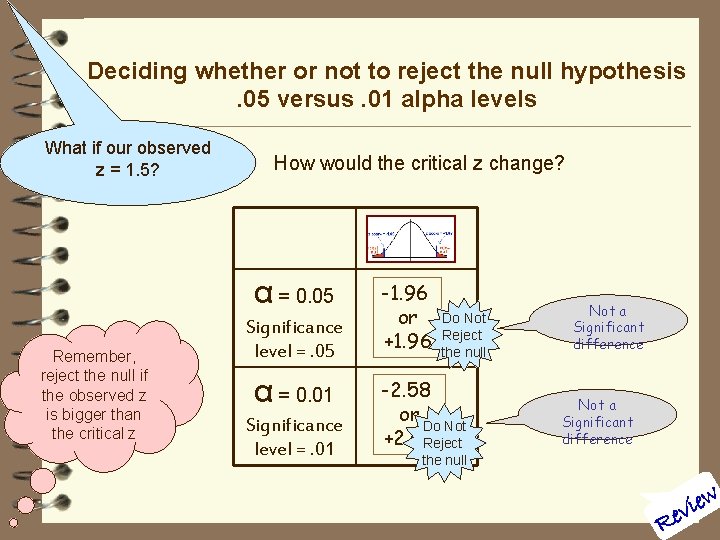
Deciding whether or not to reject the null hypothesis. 05 versus. 01 alpha levels What if our observed z = 1. 5? How would the critical z change? α = 0. 05 Remember, reject the null if the observed z is bigger than the critical z Significance level =. 05 α = 0. 01 Significance level =. 01 -1. 96 or +1. 96 Do Not Reject the null -2. 58 or Do Not +2. 58 Reject Not a Significant difference the null ew i v Re

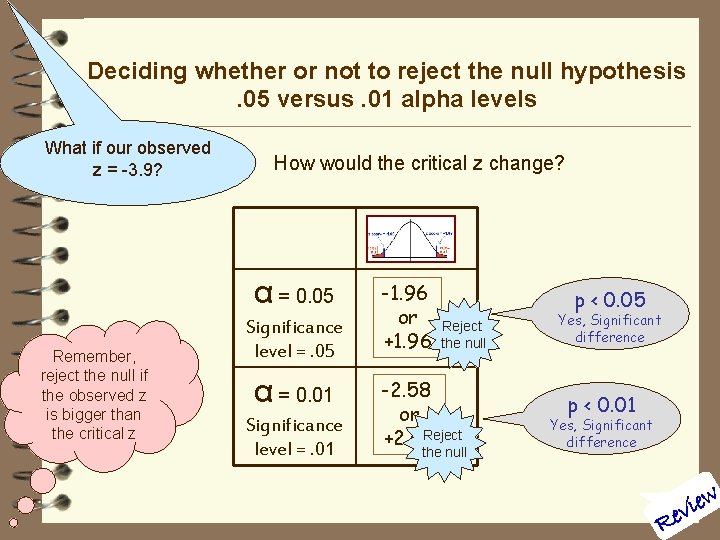
Deciding whether or not to reject the null hypothesis. 05 versus. 01 alpha levels What if our observed z = -3. 9? How would the critical z change? α = 0. 05 Remember, reject the null if the observed z is bigger than the critical z Significance level =. 05 α = 0. 01 Significance level =. 01 -1. 96 or +1. 96 p < 0. 05 Reject the null -2. 58 or Reject +2. 58 the null Yes, Significant difference p < 0. 01 Yes, Significant difference ew i v Re

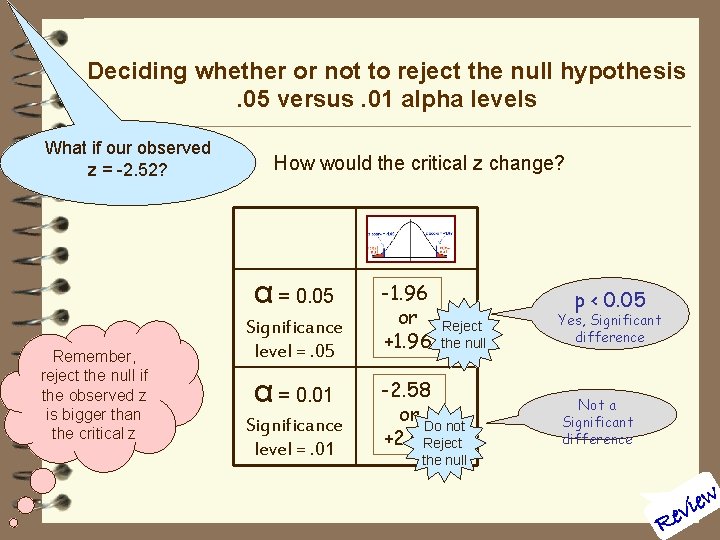
Deciding whether or not to reject the null hypothesis. 05 versus. 01 alpha levels What if our observed z = -2. 52? How would the critical z change? α = 0. 05 Remember, reject the null if the observed z is bigger than the critical z Significance level =. 05 α = 0. 01 Significance level =. 01 -1. 96 or +1. 96 p < 0. 05 Reject the null -2. 58 or Do not +2. 58 Reject Yes, Significant difference Not a Significant difference the null ew i v Re

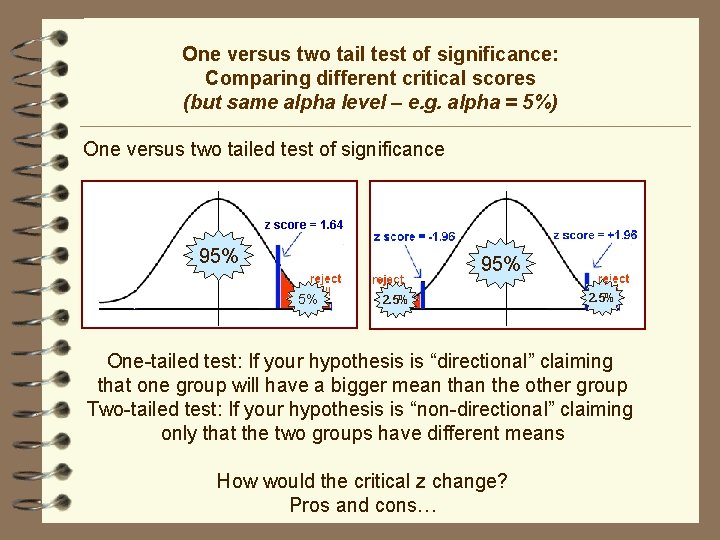
One versus two tail test of significance: Comparing different critical scores (but same alpha level – e. g. alpha = 5%) One versus two tailed test of significance z score = 1. 64 95% 5% 2. 5% One-tailed test: If your hypothesis is “directional” claiming that one group will have a bigger mean the other group Two-tailed test: If your hypothesis is “non-directional” claiming only that the two groups have different means How would the critical z change? Pros and cons…

One versus two tail test of significance 5% versus 1% alpha levels How would the critical z change? One-tailed 5% 1% α = 0. 05 Significance level =. 05 α = 0. 01 Significance level =. 01 Two-tailed 2. 5%. 5% -1. 64 or +1. 64 -1. 96 or +1. 96 -2. 33 or +2. 33 -2. 58 or +2. 58

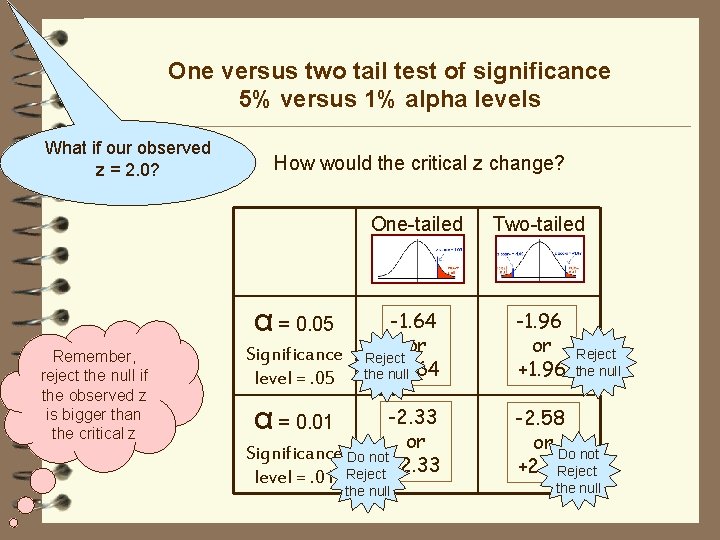
One versus two tail test of significance 5% versus 1% alpha levels What if our observed z = 2. 0? How would the critical z change? One-tailed α = 0. 05 Remember, reject the null if the observed z is bigger than the critical z Significance level =. 05 -1. 64 or Reject +1. 64 the null α = 0. 01 -2. 33 or Significance Do not +2. 33 level =. 01 Reject the null Two-tailed -1. 96 or +1. 96 Reject the null -2. 58 or Do not +2. 58 Reject the null

One versus two tail test of significance 5% versus 1% alpha levels What if our observed z = 1. 75? How would the critical z change? One-tailed α = 0. 05 Remember, reject the null if the observed z is bigger than the critical z Significance level =. 05 -1. 64 or Reject +1. 64 the null α = 0. 01 -2. 33 or Significance Do not +2. 33 level =. 01 Reject the null Two-tailed -1. 96 or +1. 96 Do not Reject the null -2. 58 or Do not +2. 58 Reject the null

One versus two tail test of significance 5% versus 1% alpha levels What if our observed z = 2. 45? How would the critical z change? One-tailed α = 0. 05 Remember, reject the null if the observed z is bigger than the critical z Significance level =. 05 α = 0. 01 -1. 64 or Reject +1. 64 the null -2. 33 or Significance Reject +2. 33 level =. 01 the null Two-tailed -1. 96 or +1. 96 Reject the null -2. 58 or Do not +2. 58 Reject the null

Standard deviation and Variance For Sample and Population These would be helpful to know by heart – please memorize these formula w ie v Re

Five steps to hypothesis testing Step 1: Identify the research problem (hypothesis) Describe the null and alternative hypotheses Step 2: Decision rule • • Alpha level? (α =. 05 or. 01)? One or two tailed test? Balance between Type I versus Type II error Critical statistic (e. g. z or t or F or r) value? Step 3: Calculations Step 4: Make decision whether or not to reject null hypothesis If observed z (or t) is bigger then critical z (or t) then reject null Step 5: Conclusion - tie findings back in to research problem

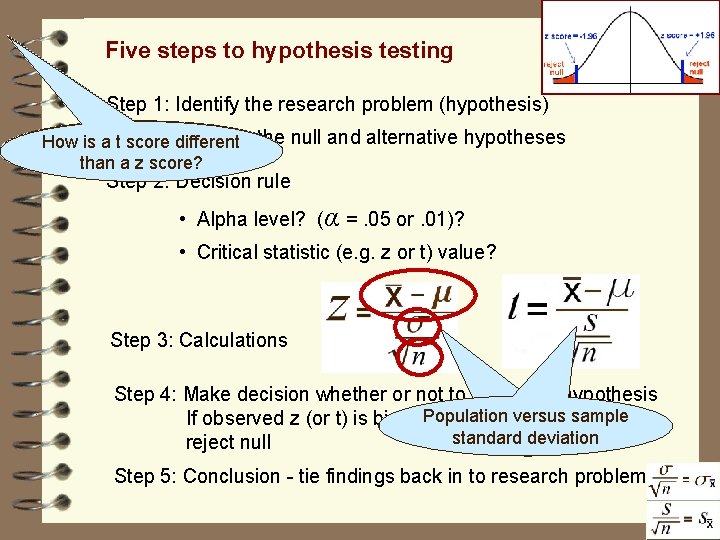
Five steps to hypothesis testing Step 1: Identify the research problem (hypothesis) the null and alternative hypotheses Howisisaat score. Describe same How different as aazzscore? than score? Step 2: Decision rule • Alpha level? (α =. 05 or. 01)? • Critical statistic (e. g. z or t) value? Step 3: Calculations Step 4: Make decision whether or not to reject null hypothesis versus sample If observed z (or t) is bigger. Population then critical z (or t) then standard deviation reject null Step 5: Conclusion - tie findings back in to research problem

Hypothesis testing: one sample t-test Let’s ju and d mp right i n o a ttest Is the mean of my observed sample consistent with the known population mean or did it come from some other distribution? We are given the following problem: 800 students took a chemistry exam. Accidentally, 25 students got an additional ten minutes. Did this extra time make a significant difference in the scores? The average number correct by the large class was 74. The scores for the sample of 25 was 76, 72, 78, 80, 73 70, 81, 75, 79, 76 77, 79, 81, 74, 62 95, 81, 69, 84, 76 75, 77, 74, 72, 75 Please note: In this example we are comparing our sample mean with the population mean (One-sample t-test)

Hypothesis testing Extra time Independent Step 1: Identify the research problem / hypothesis Dependen Test t of students affect Scores IV: Nominal IV: DV: Nominal Ordinal Variable? Nominal vs. no extra time Variable? Did the extra time given to this sample their chemistry test scores? Ordinal Ratio Interval or One tail or Ratio? Two-tailed Ratio? two tail test? Null: The extra time did not affect their chemistry test scores Alternative: The extra time did affect their chemistry test scores

Hypothesis testing Step 2: Decision rule =. 05 n = 25 n– 1 What is formula for degres of freedom? Degrees of freedom (df) = (n - 1)= (25 - 1) = 24 two tail test

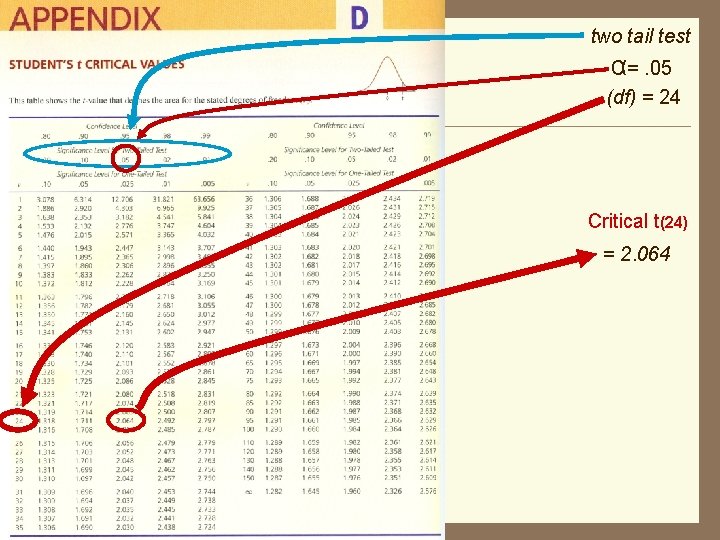
two tail test α=. 05 (df) = 24 Critical t(24) = 2. 064

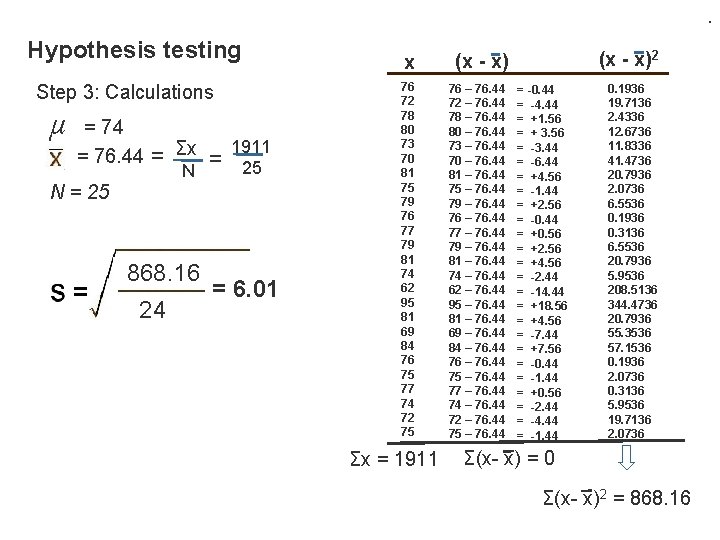
. Hypothesis testing Step 3: Calculations µ = 74 = 76. 44 N = 25 = Σx = N 868. 16 24 1911 25 = 6. 01 x (x - x) 76 72 78 80 73 70 81 75 79 76 77 79 81 74 62 95 81 69 84 76 75 77 74 72 75 76 – 76. 44 72 – 76. 44 78 – 76. 44 80 – 76. 44 73 – 76. 44 70 – 76. 44 81 – 76. 44 75 – 76. 44 79 – 76. 44 76 – 76. 44 77 – 76. 44 79 – 76. 44 81 – 76. 44 74 – 76. 44 62 – 76. 44 95 – 76. 44 81 – 76. 44 69 – 76. 44 84 – 76. 44 76 – 76. 44 75 – 76. 44 77 – 76. 44 74 – 76. 44 72 – 76. 44 75 – 76. 44 Σx = 1911 (x - x)2 = -0. 44 = -4. 44 = +1. 56 = + 3. 56 = -3. 44 = -6. 44 = +4. 56 = -1. 44 = +2. 56 = -0. 44 = +0. 56 = +2. 56 = +4. 56 = -2. 44 = -14. 44 = +18. 56 = +4. 56 = -7. 44 = +7. 56 = -0. 44 = -1. 44 = +0. 56 = -2. 44 = -4. 44 = -1. 44 0. 1936 19. 7136 2. 4336 12. 6736 11. 8336 41. 4736 20. 7936 2. 0736 6. 5536 0. 1936 0. 3136 6. 5536 20. 7936 5. 9536 208. 5136 344. 4736 20. 7936 55. 3536 57. 1536 0. 1936 2. 0736 0. 3136 5. 9536 19. 7136 2. 0736 Σ(x- x) = 0 Σ(x- x)2 = 868. 16

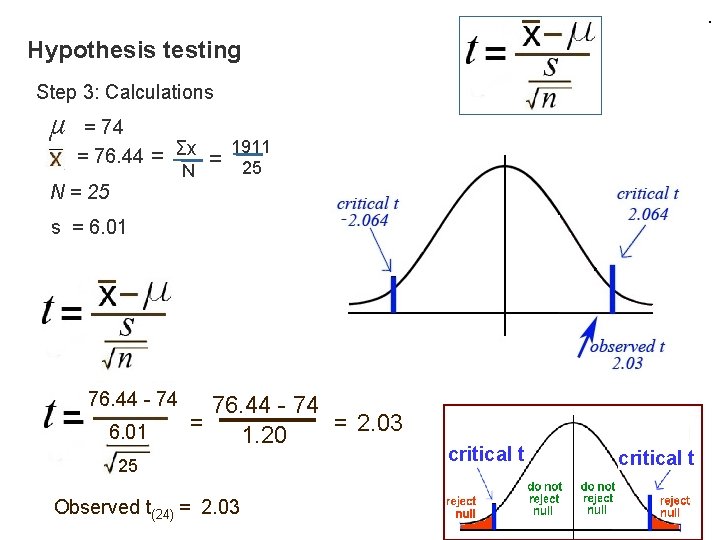
. Hypothesis testing Step 3: Calculations µ = 74 = 76. 44 N = 25 = Σx = N 1911 25 s = 6. 01 76. 44 - 74 = = 2. 03 1. 20 25 Observed t(24) = 2. 03 critical t

. Hypothesis testing Step 4: Make decision whether or not to reject null hypothesis Observed t(24) = 2. 03 Critical t(24) = 2. 064 2. 03 is not farther out on the curve than 2. 064, so, we do not reject the null hypothesis Step 6: Conclusion: The extra time did not have a significant effect on the scores

. Hypothesis testing: Did the extra time given to these 25 students affect their average test score? Start summary with two means (based on DV) for two levels of the IV Describe type of test (t-test versus z-test) with brief overview of results Finish with statistical summary t(24) = 2. 03; ns notice we are comparing a sample mean with a population mean: single sample t-test Or if it had been different results that *were* significant: t(24) = -5. 71; p < 0. 05 The mean score for those students who where given extra time was 76. 44 percent correct, while the mean score for the rest of the class was only 74 percent correct. A t-test was completed and there appears to be no significant difference in the test scores for these two groups t(24) = 2. 03; n. s. Type of test with degrees of freedom Value of observed statistic n. s. = “not significant” p<0. 05 = “significant”