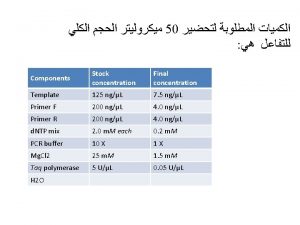
Introduction to Statistics Concentration on applied statistics Statistics









































- Slides: 50

Introduction to Statistics • Concentration on applied statistics • Statistics appropriate for measurement • Today’s lecture will cover basic concepts – You should already be familiar with these © 1998, Geoff Kuenning

Independent Events • Occurrence of one event doesn’t affect probability of other • Examples: – Coin flips – Inputs from separate users – “Unrelated” traffic accidents • What about second basketball free throw after the player misses the first? © 1998, Geoff Kuenning

Random Variable • Variable that takes values with a specified probability • Variable usually denoted by capital letters, particular values by lowercase • Examples: – Number shown on dice – Network delay • What about disk seek time? © 1998, Geoff Kuenning

Cumulative Distribution Function (CDF) • Maps a value a to probability that the outcome is less than or equal to a: • Valid for discrete and continuous variables • Monotonically increasing • Easy to specify, calculate, measure © 1998, Geoff Kuenning

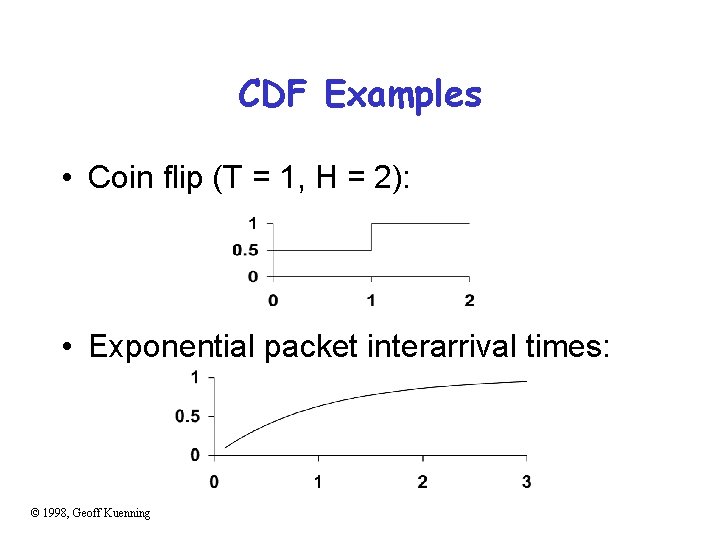
CDF Examples • Coin flip (T = 1, H = 2): • Exponential packet interarrival times: © 1998, Geoff Kuenning

Probability Density Function (pdf) • Derivative of (continuous) CDF: • Usable to find probability of a range: © 1998, Geoff Kuenning

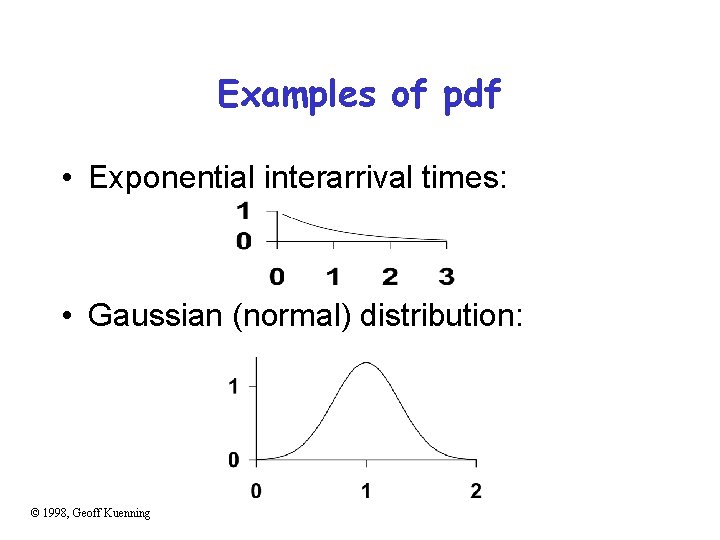
Examples of pdf • Exponential interarrival times: • Gaussian (normal) distribution: © 1998, Geoff Kuenning

Probability Mass Function (pmf) • CDF not differentiable for discrete random variables • pmf serves as replacement: f(xi) = pi where pi is the probability that x will take on the value xi © 1998, Geoff Kuenning

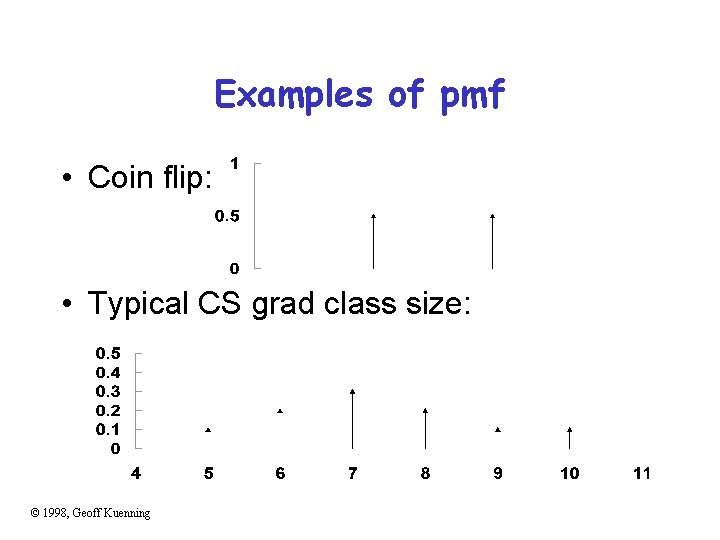
Examples of pmf • Coin flip: • Typical CS grad class size: © 1998, Geoff Kuenning

Expected Value (Mean) • Mean • Summation if discrete • Integration if continuous © 1998, Geoff Kuenning

Variance & Standard Deviation • Var(x) = • Usually denoted 2 • Square root is called standard deviation © 1998, Geoff Kuenning

Coefficient of Variation (C. O. V. or C. V. ) • Ratio of standard deviation to mean: • Indicates how well mean represents the variable © 1998, Geoff Kuenning

Covariance • Given x, y with means x and y, their covariance is: – typos on p. 181 of book • High covariance implies y departs from mean whenever x does © 1998, Geoff Kuenning

Covariance (cont’d) • For independent variables, E(xy) = E(x)E(y) so Cov(x, y) = 0 • Reverse isn’t true: Cov(x, y) = 0 doesn’t imply independence • If y = x, covariance reduces to variance © 1998, Geoff Kuenning

Correlation Coefficient • Normalized covariance: • Always lies between -1 and 1 • Correlation of 1 x ~ y, -1 © 1998, Geoff Kuenning

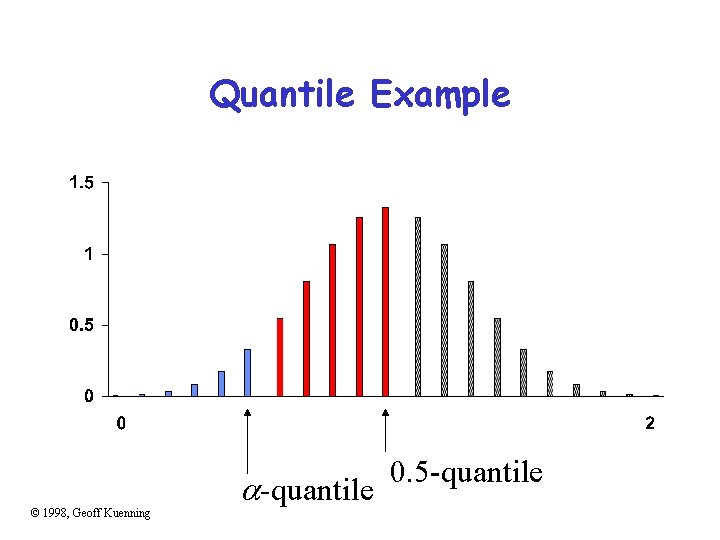
Quantile • x value at which CDF takes a value is called a-quantile or 100 -percentile, denoted by x. • If 90 th-percentile score on GRE was 1500, then 90% of population got 1500 or less © 1998, Geoff Kuenning

Quantile Example © 1998, Geoff Kuenning -quantile 0. 5 -quantile

Median • 50 -percentile (0. 5 -quantile) of a random variable • Alternative to mean • By definition, 50% of population is submedian, 50% super-median – Lots of bad (good) drivers – Lots of smart (stupid) people © 1998, Geoff Kuenning

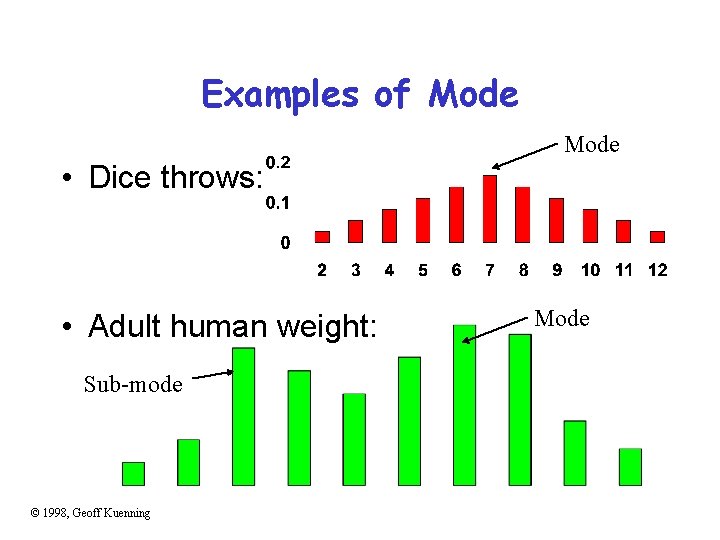
Mode • Most likely value, i. e. , xi with highest probability pi, or x at which pdf/pmf is maximum • Not necessarily defined (e. g. , tie) • Some distributions are bi-modal (e. g. , human height has one mode for males and one for females) © 1998, Geoff Kuenning

Examples of Mode • Dice throws: • Adult human weight: Sub-mode © 1998, Geoff Kuenning Mode

Normal (Gaussian) Distribution • Most common distribution in data analysis • pdf is: • - x + • Mean is , standard deviation © 1998, Geoff Kuenning

Notation for Gaussian Distributions • Often denoted N( , ) • Unit normal is N(0, 1) • If x has N( , ), has N(0, 1) • The -quantile of unit normal z ~ N(0, 1) is denoted z so that © 1998, Geoff Kuenning

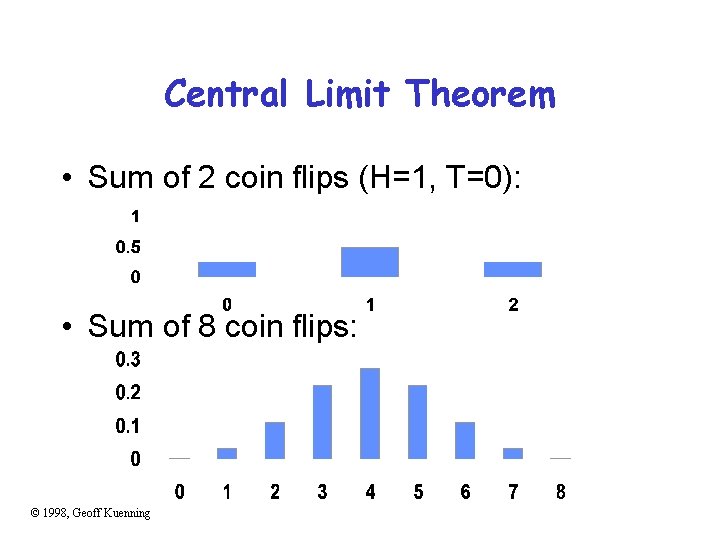
Why Is Gaussian So Popular? • If xi ~ N( , ) and all xi independent, then ixi is normal with mean i i and variance i 2 • Sum of large no. of independent observations from any distribution is itself normal (Central Limit Theorem) Experimental errors can be modeled as normal distribution. © 1998, Geoff Kuenning

Central Limit Theorem • Sum of 2 coin flips (H=1, T=0): • Sum of 8 coin flips: © 1998, Geoff Kuenning

Measured Data But, we don’t know F(x) – all we have is a bunch of observed values – a sample. What is a sample? – Example: How tall is a human? • Could measure every person in the world (actually even that’s a sample) • Or could measure every person in this room – Population has parameters – Sample has statistics • Drawn from population • Inherently erroneous © 1998, Geoff Kuenning

Central Tendency • Sample mean – x (arithmetic mean) – Take sum of all observations and divide by the number of observations • Sample median – Sort the observations in increasing order and take the observation in the middle of the series • Sample mode – Plot a histogram of the observations and choose the midpoint of the bucket where the histogram peaks © 1998, Geoff Kuenning

Indices of Dispersion • Measures of how much a data set varies – Range – Sample variance – And derived from sample variance: • Square root -- standard deviation, S • Ratio of sample mean and standard deviation – COV s/x – Percentiles • Specification of how observations fall into buckets © 1998, Geoff Kuenning

Interquartile Range • Yet another measure of dispersion • The difference between Q 3 and Q 1 • Semi-interquartile range - • Often interesting measure of what’s going on in the middle of the range © 1998, Geoff Kuenning

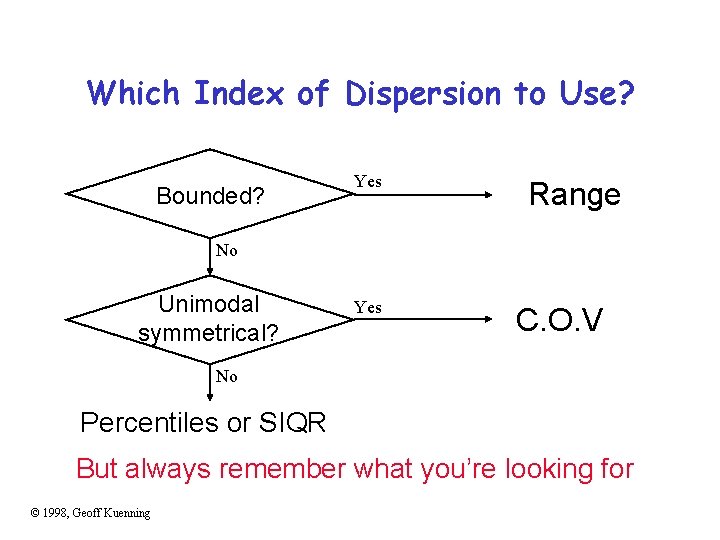
Which Index of Dispersion to Use? Bounded? Yes Range No Unimodal symmetrical? Yes C. O. V No Percentiles or SIQR But always remember what you’re looking for © 1998, Geoff Kuenning

Determining a Distribution for a Data Set • If a data set has a common distribution, that’s the best way to summarize it – Saying a data set is uniformly distributed is more informative than just giving its sample mean and standard deviation • So how do you determine if your data set fits a distribution? – Plot a histogram – Quantile-quantile plot – Statistical methods © 1998, Geoff Kuenning

Quantile-Quantile Plots • Most suitable for small data sets • Basically -- guess a distribution • Plot where quantiles of data should fall in that distribution – Against where they actually fall in the sample • If plot is close to linear, data closely matches that distribution © 1998, Geoff Kuenning

Obtaining Theoretical Quantiles • We need to determine where the quantiles should fall for a particular distribution • Requires inverting the CDF for that distribution qi = F(xi) t xi = F-1(qi) – Then determining quantiles for observed points – Then plugging in quantiles to inverted CDF © 1998, Geoff Kuenning

Inverting a Distribution • Many common distributions have already been inverted (how convenient…) • For others that are hard to invert, tables and approximations are often available (nearly as convenient) © 1998, Geoff Kuenning

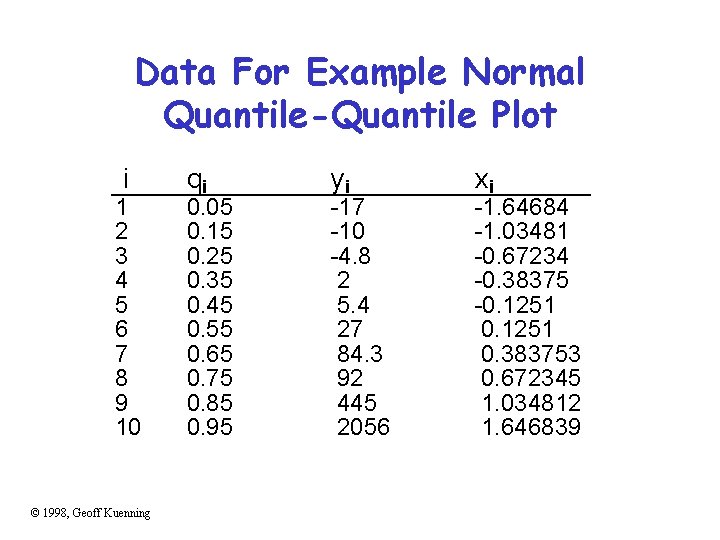
Is Our Example Data Set Normally Distributed? • Our example data set was -17, -10, -4. 8, 2, 5. 4, 27, 84. 3, 92, 445, 2056 • Does this match the normal distribution? • The normal distribution doesn’t invert nicely – But there is an approximation for N(0, 1): – Or invert numerically © 1998, Geoff Kuenning

Data For Example Normal Quantile-Quantile Plot i 1 2 3 4 5 6 7 8 9 10 © 1998, Geoff Kuenning qi 0. 05 0. 15 0. 25 0. 35 0. 45 0. 55 0. 65 0. 75 0. 85 0. 95 yi -17 -10 -4. 8 2 5. 4 27 84. 3 92 445 2056 xi -1. 64684 -1. 03481 -0. 67234 -0. 38375 -0. 1251 0. 383753 0. 672345 1. 034812 1. 646839

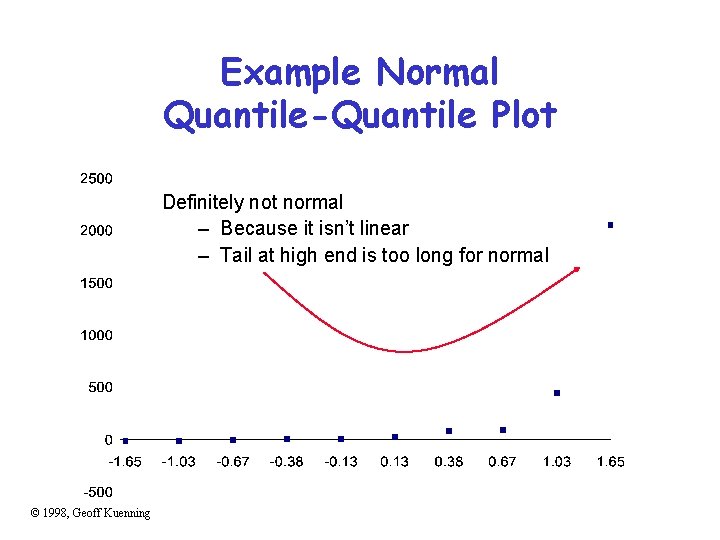
Example Normal Quantile-Quantile Plot Definitely not normal – Because it isn’t linear – Tail at high end is too long for normal © 1998, Geoff Kuenning

Estimating Population from Samples • How tall is a human? – Measure everybody in this room – Calculate sample mean – Assume population mean equals • What is the error in our estimate? © 1998, Geoff Kuenning

Estimating Error • Sample mean is a random variable Mean has some distribution Multiple sample means have “mean of means” • Knowing distribution of means can estimate error © 1998, Geoff Kuenning

Confidence Intervals • Sample mean value is only an estimate of the true population mean • Bounds c 1 and c 2 such that there is a high probability, 1 - , that the population mean is in the interval (c 1, c 2): Prob{ c 1 < m < c 2} =1 - where is the significance level and 100(1 - ) is the confidence level • Overlapping confidence intervals is interpreted as “not statistically different”

Confidence Intervals • How tall is Fred? – Suppose average human height is 170 cm Fred is 170 cm tall Yeah, right – Suppose 90% of humans are between 155 and 190 cm Fred is between 155 and 190 cm • We are 90% confident that Fred is between 155 and 190 cm © 1998, Geoff Kuenning

Confidence Interval of Sample Mean • Knowing where 90% of sample means fall, we can state a 90% confidence interval • Key is Central Limit Theorem: – Sample means are normally distributed – Only if independent – Mean of sample means is population mean – Standard deviation (standard error) is © 1998, Geoff Kuenning

Estimating Confidence Intervals • Two formulas for confidence intervals – Over 30 samples from any distribution: z-distribution – Small sample from normally distributed population: t-distribution • Common error: using t-distribution for non-normal population – Central Limit Theorem often saves us © 1998, Geoff Kuenning

The z Distribution • Interval on either side of mean: • Significance level is small for large confidence levels • Tables of z are tricky: be careful! © 1998, Geoff Kuenning

Example of z Distribution • 35 samples: 10 16 47 48 74 30 81 42 57 67 7 13 56 44 54 17 60 32 45 28 33 60 36 59 73 46 10 40 35 65 34 25 18 48 63 • Sample mean = 42. 1. Standard deviation s = 20. 1. n = 35 • 90% confidence interval is © 1998, Geoff Kuenning

The t Distribution • Formula is almost the same: • Usable only for normally distributed populations! • But works with small samples © 1998, Geoff Kuenning

Example of t Distribution • 10 height samples: 148 166 170 191 187 114 168 180 177 204 • Sample mean = 170. 5. Standard deviation s = 25. 1, n = 10 • 90% confidence interval is • 99% interval is (144. 7, 196. 3) © 1998, Geoff Kuenning

Getting More Confidence • Asking for a higher confidence level widens the confidence interval – Counterintuitive? • How tall is Fred? – 90% sure he’s between 155 and 190 cm – We want to be 99% sure we’re right – So we need more room: 99% sure he’s between 145 and 200 cm © 1998, Geoff Kuenning

For Discussion Next Tuesday Project Proposal 1. Statement of hypothesis 2. Workload decisions 3. Metrics to be used 4. Method Reading for Next Time Elson, Girod, Estrin, “Fine-grained Network Time Synchronization using Reference Broadcasts, OSDI 2002 – see readings. html

For Discussion Today • Bring in one either notoriously bad or exceptionally good example of data presentation from your proceedings. The bad ones are more fun. Or if you find something just really different, please show it.

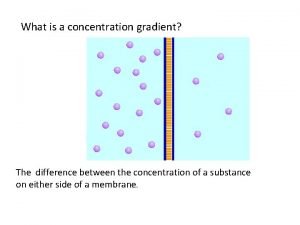
 Concentration gradient
Concentration gradient Movement of high concentration to low concentration
Movement of high concentration to low concentration Introduction to statistics what is statistics
Introduction to statistics what is statistics Applied statistics and probability for engineers download
Applied statistics and probability for engineers download Applied business statistics ken black pdf
Applied business statistics ken black pdf Applied business statistics ken black
Applied business statistics ken black An introduction to applied linguistics
An introduction to applied linguistics Introduction to statistics worksheet
Introduction to statistics worksheet Introduction to statistics and some basic concepts
Introduction to statistics and some basic concepts Introduction to descriptive statistics
Introduction to descriptive statistics Introduction to statistics chapter 1
Introduction to statistics chapter 1 Introduction to bayesian statistics
Introduction to bayesian statistics Introduction to elementary statistics
Introduction to elementary statistics Statistics a gentle introduction
Statistics a gentle introduction A modern introduction to probability and statistics
A modern introduction to probability and statistics Chapter 1 introduction to statistics
Chapter 1 introduction to statistics Introduction to statistics in ap biology
Introduction to statistics in ap biology Percentile example
Percentile example Introduction to educational statistics
Introduction to educational statistics Dachau visite virtuelle
Dachau visite virtuelle Measures of concentration molarity quiz
Measures of concentration molarity quiz Four firm concentration ratio
Four firm concentration ratio Concentration mole volume
Concentration mole volume Selective specialization example
Selective specialization example Diffusion facilitée
Diffusion facilitée Moles triangle concentration
Moles triangle concentration Bradford reagent structure
Bradford reagent structure Dilution equation
Dilution equation Molality
Molality Mass percent
Mass percent Concentration ratio
Concentration ratio Equation
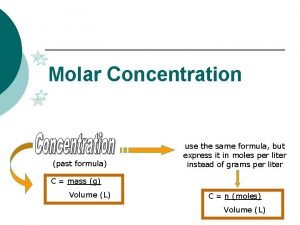
Equation Measures of concentration molarity
Measures of concentration molarity How is molarity measured
How is molarity measured Is molarity and concentration the same
Is molarity and concentration the same Molarity
Molarity Molarity to concentration
Molarity to concentration Ketamine concentration
Ketamine concentration Mba investment management concentration
Mba investment management concentration Four-firm concentration ratio
Four-firm concentration ratio What is catalystfive
What is catalystfive Density of states semiconductor
Density of states semiconductor Astenent
Astenent Gradient de concentration
Gradient de concentration Blood alcohol concentration (bac)
Blood alcohol concentration (bac) Flow rate concentration equation
Flow rate concentration equation Classification of inhalational agents
Classification of inhalational agents Inhalation anesthetics
Inhalation anesthetics Classification of inhalational agents
Classification of inhalational agents Sucrose solubility curve
Sucrose solubility curve Economy of a multiple effect evaporator depends upon the
Economy of a multiple effect evaporator depends upon the