Introduction to Statistics Basic Concepts Intro to Statistics

Introduction to Statistics Basic Concepts

Intro. to Statistics n What is Statistics? • “…a set of procedures and rules…for reducing large masses of data to manageable proportions and for allowing us to draw conclusions from those data”

Intro. to Statistics n What can Stats do? • Make data more manageable n Group of numbers: 6, 1, 8, 3, 5, 4, 9 n n Average is: 36/7 = 5 1/7 Graphs:

Intro. to Statistics n What can Stats do? • Allow us to draw conclusions from the data Group of numbers #1: 6, 1, 8, 3, 5, 4, 9 n Average is 5 1/7 n Group of numbers #2: 8, 3, 4, 2, 7, 1, 4 n Average is 4 ¼ n • Allows us to do this objectively and quantitatively

Intro. to Statistics n “Quantitative” • Involves measurement • Data in numerical form • Answers “How much” questions • Objective and results in unambiguous conclusions n “Qualitative” • Describes the nature of something • Answers “What” or “Of what kind” questions • Often evaluative and ambiguous

Intro. to Statistics n Qualitative Distinctions: • “Good” versus “Bad” • “Right” versus “Wrong” • “A Lot” versus “A Little” n Quantitative Distinctions: • 5 1/7 versus 4 ¼ • 25% versus 50% • 1 hour versus 24 hours

Basic Terminology n n n Summarizing versus Analyzing Descriptive Statistics Inferential Statistics • • • Inference from sample to population Inference from statistic to parameter Factors influencing the accuracy of a sample’s ability to represent a population: n n Size Randomness

Basic Terminology • Size – n Sample of 5 cards from a deck of 52 • 2 of Clubs, 10 of Diamonds, Jack of Hearts, 5 of Clubs, and 7 of Hearts What could we conclude about the full deck from this sample about what the full deck looks like without any prior knowledge of a deck of cards? n Compare this to a sample of 51/52 cards – What could we conclude from this sample? n

Basic Terminology • Randomness – n This time lets use the same 5 card sample, but this time the deck is unshuffled (nonrandom) • 2 of Clubs, 10 of Clubs, Jack of Clubs, 5 of Clubs, and 7 of Clubs n What would we conclude about the characteristics of our population (the deck) this time versus when the sample was more random (shuffled)?

Basic Terminology n Smaller/less random samples both poorly represent population of entire deck of cards • Also result in inaccurate inferences about population – poor external validity

Basic Terminology n Most often, the aim of our research is not to infer characteristics of a population from our sample, but to compare two samples • I. e. To determine if a particular treatment works, we compare two groups or samples, one with the treatment and one without

Basic Terminology • We draw conclusions based on how similar the two groups are n n If the treated and untreated groups are very similar, we cannot declare the treatment much of a success Another way of putting this in terms of samples and populations is determining if our two groups/samples actually come from the same population, or two different ones

Basic Terminology n Group A (Treated) and B (Untreated) are sampled from different populations/treatment worked: Group A Population of Well People Group B Population of Sick People

Basic Terminology n Group A and B are sampled from the same population/treatment didn’t work: Group A Group B Population of Sick People

Basic Terminology n What if Group A (who received the Tx) were sicker then Group B (who did not receive Tx), prior to treatment? What would their scores look like after Tx? • The inability to attribute changes in the variable of interest to the manipulation – poor internal validity n I. e. we can’t say for sure if our experiment worked or not

Basic Terminology n Quantitative Data • Dimensional/Measurement Data versus Categorical/Frequency Count Data n Dimensional • When quantities of something are measured on a continuum • Answers “how much” questions • I. e. scores on a test, measures of weight, etc.

Basic Terminology n Categorical • When numbers of discrete entities have to be counted n Gender is an example of a discrete entity – you can be either male or female, and nothing else – speaking of “degree of maleness” makes little sense • Answers “how many” questions • I. e. number of men and women, percentage of people with a given hair color

Basic Terminology n A dimensional variable can be converted into a categorical one • Convert scores on a test (0 -100) into “Low”, “Medium”, and “High” groups – 0 -33 = Low; 34 -66 = Medium, and 67100 = High n The groups are discrete categories (hence “categorical”), and you would now count how many people fall into each category

Basic Concepts n Scales of Measurement: • Nominal n n n labeling/classifying objects i. e. your last name, names on jerseys, social security number, etc. not technically a scale of measurement since nothing is measured • Ordinal n n n labels that imply rank i. e. place in a race, military rank – 1 st > 2 nd > 3 rd and General > Lieutenant > Private doesn’t say how much more one is than the other

Basic Concepts n Interval • provides labels that imply exactly how much different one label is than another • i. e. temperature - 15° F is 5 ° F more than 10 ° F • lacks true zero point - 0 ° F does not represent the complete absence of heat because we have negative values of °F n Ratio • • has all of the above, plus a true zero point i. e. height, weight, ° Kelvin – 0 lbs represents a true lack of weight • can talk about 16 ° being four times 4 °, which is a proportion /ratio, hence the name of the scale - x = 4 y • often very difficult to identify in practice if a true zero point exists

Basic Concepts n Scales of Measurement • Nominal • Qualitative • Ordinal • Interval • Ratio • Quantitative

Basic Concepts n Variables • Discrete versus Continuous Variables n same as Categorical versus Dimensional variables • Not to be confused with “discreet” variables, that people simply do not think should be talked about

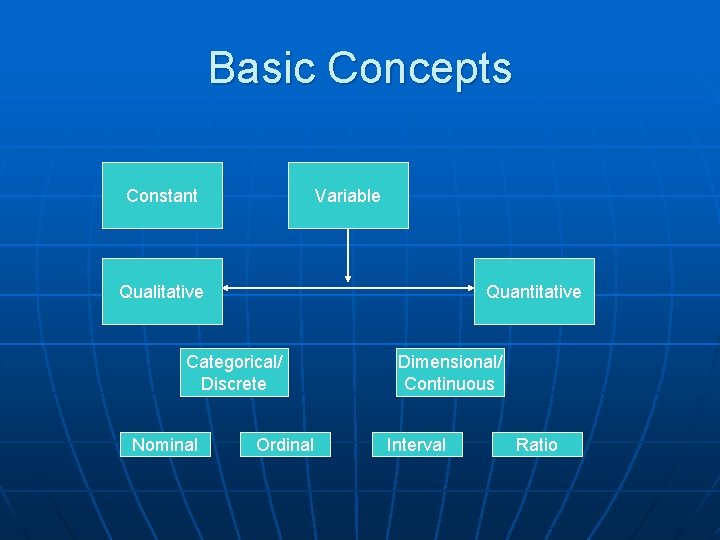
Basic Concepts Constant Variable Qualitative Quantitative Categorical/ Discrete Nominal Ordinal Dimensional/ Continuous Interval Ratio

Basic Concepts n Variables versus Constants • A constant has only one possible value that it can assume n π = 3. 1415923536… • A variable can assume many possible values n n X=? Independent Variables (IV’s) versus Dependent Variables (DV’s) • IV manipulated, DV measured • Whether a variable is a DV or IV depends upon the design of the experiment

Basic Concepts n Variables • In true experiments, the effects of one variable (the IV) are manipulated to see the effects on another variable (the DV) • All other factors other than the IV are kept constant so that we can attribute the change to the IV and not to something else • Example: Influence of direct heat on the temperature of water n n IV = presence or absence of heat DV = temperature of water