Introduction to SQL the Structured Query Language Zachary

Introduction to SQL, the Structured Query Language Zachary G. Ives University of Pennsylvania CIS 550 – Database & Information Systems September 16, 2003 Some slide content courtesy of Susan Davidson & Raghu Ramakrishnan

Administrivia § Homework 1 due Thursday, on paper at start of class (electronic submission to Dinkar is also OK) § Homework 2 will be handed out Thursday § Will involve writing SQL § We should have Oracle available for you on eniac § Groups and project choices due by email by end of Friday – send to zives@cis, dinkar@gradient. cis § Groups will be given supplemental reading to help them on their projects 2

Recall the Relational Algebra § Relational algebra operations operate on relations and produce relations (“closure”) f: Relation -> Relation § Six basic operations: § § § Projection Selection Union Difference Product (Rename) f: Relation x Relation -> Relation A (R) R 1 [ R 2 R 1 – R 2 R 1 £ R 2 A->B (R) § And some other useful ones: § § Join Semijoin Intersection Division R 1 ⋈ R 2 R 1 ⊲ R 2 R 1 Å R 2 R 1 ¥ R 2 3

Recall the Domain Relational Calculus Queries of form: domain variables {<x 1, x 2, …, xn>| p} predicate Predicate: boolean expression over x 1, x 2, …, xn § Expressions: <xi, xj, …> R X op Y X op const op X where op is , , , xi, xj, … are domain variables § Complex expressions: e 1 e 2, e, and e 1 e 2 § Universal and existential quantifiers 4

Tuple. Relational Calculus Queries of form: domain variables {<Ti. attria, Tj. attrjb, …, Tn. attrnm>| p} predicate Predicate: boolean expression over Tx attribs § Expressions: Tx R TX. a op TY. b TX. a op const op TX. a where op is , , , Tx, … are tuple variables, Tx. a, … are attributes § Complex expressions: e 1 e 2, e, and e 1 e 2 § Universal and existential quantifiers 5

From the Abstract to the Concrete Can’t do: § Aggregate operations § Recursive queries § Complex (non-tabular) structures § Today we’ll see SQL, which is relationally complete and can also do the first two things 6

Basic SQL: A Friendly Face Over the. Tuple. Relational Calculus SELECT [DISTINCT] {T 1. attrib , …, T 2. attrib } FROM {relation } T 1, {relation } T 2, … select-list WHERE {predicates } from-list qualification Let’s do some examples, which will leverage your knowledge of the relational calculus… § Faculty ids § Course IDs for courses with students expecting a “C” § Courses taken by Jill 7

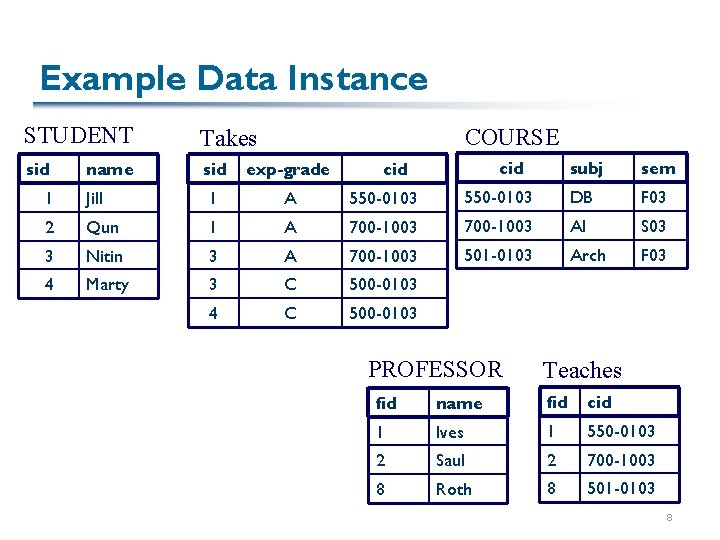
Example Data Instance STUDENT Takes sid exp-grade name COURSE cid subj sem 1 Jill 1 A 550 -0103 DB F 03 2 Qun 1 A 700 -1003 AI S 03 3 Nitin 3 A 700 -1003 501 -0103 Arch F 03 4 Marty 3 C 500 -0103 4 C 500 -0103 PROFESSOR Teaches fid name fid cid 1 Ives 1 550 -0103 2 Saul 2 700 -1003 8 Roth 8 501 -0103 8

Some Nice Features § SELECT * § All STUDENTs § AS § As a “range variable” (tuple variable): optional § As an attribute rename operator § Revisit last Thursday’s TRC query: § Which students (names) have taken more than one course from the same professor? § But rename the student name to “person” 9

Expressions in SQL § Can do computation over scalars (int, real or string) in the select-list or the qualification § Show all student IDs decremented by 1 § Strings: § § Fixed (CHAR(x)) or variable length (VARCHAR(x)) Use single quotes: ’A string’ Special comparison operator: LIKE Not equal: <> § Typecasting: § CAST(S. sid AS VARCHAR(255)) 10

Set Operations § Set operations default to set semantics, not bag semantics: (SELECT … FROM … WHERE …) {op} (SELECT … FROM … WHERE …) § Where op is one of: § UNION § INTERSECT, MINUS/EXCEPT (many DBs don’t support these last ones!) § Bag semantics: ALL 11

Exercise § Find all students who have taken DB but not AI § Hint: use EXCEPT 12

Nested Queries in SQL § Simplest: IN/NOT IN § Example: Students who have taken subjects that have (at any point) been taught by Roth 13

Correlated. Subqueries § Most common: EXISTS/NOT EXISTS § Find all students who have taken DB but not AI 14

Universal and Existential Quantification § Generally used with subqueries: § {op} ANY, {op} ALL § Find the students with the best expected grades 15

Table Expressions § Can substitute a subquery for any relation in the FROM clause: SELECT S. sid FROM (SELECT sid FROM STUDENT WHERE sid = 5) S WHERE S. sid = 4 Notice that we can actually simplify this query! What is this equivalent to? 16

Aggregation § GROUP BY SELECT {group- attribs }, {aggregate- operator }(attrib ) FROM {relation } T 1, {relation } T 2, … WHERE {predicates } GROUP BY {group-list } § Aggregate operators § AVG, COUNT, SUM, MAX, MIN § DISTINCT keyword for AVG, COUNT, SUM 17

Some Examples § Number of students in each course offering § Number of different grades expected for each course offering § Number of (distinct) students taking AI courses 18

What If You Want to Only Show Some Groups? § The HAVING clause lets you do a selection based on an aggregate (there must be 1 value per group): SELECT C. subj, COUNT(S. sid) FROM STUDENT S, Takes T, COURSE C WHERE S. sid = T. sid AND T. cid = C. cid GROUP BY subj HAVING COUNT(S. sid) > 5 § Exercise: For each subject taught by at least two professors, list the minimum expected grade 19

Aggregation and Table Expressions § Sometimes need to compute results over the results of a previous aggregation: SELECT subj, AVG(size) FROM ( SELECT C. cid AS id, C. subj AS subj, COUNT(S. sid) AS size FROM STUDENT S, Takes T, COURSE C WHERE S. sid = T. sid AND T. cid = C. cid GROUP BY cid, subj) GROUP BY subj 20

Something to Ponder § Tables are great, but… § Not everyone is uniform – I may have a cell phone but not a fax § We may simply be missing certain information § We may be unsure about values § How do we handle these things? 21

Remember… § Homework 1 due Thursday § Groups and project choices due by email by end of Friday – send to zives@cis, dinkar@gradient. cis 22