Introduction to Sets 1 6 Sets set object


Introduction to Sets 1. 6 Sets 정의 • 집합(set)이란 순서를 고려하지 않고 중복을 고려하지 않는 객체(object)들의 모임이다. • A set is a new type of structure, representing an unordered collection (group) of zero or more distinct (different) objects. Basic notations for sets • For sets, we’ll use variables S, T, U, … • We can denote a set S in writing by listing all of its elements in curly braces { and }: {a, b, c} is the set of whatever three objects are denoted by a, b, c. • Set builder notation: {x|P(x)} means the set of all x such that P(x). 원소 나열법 (예: {…, -3, -2, -1, 0, 1, 2, 3, …}) 조건 제시법 (예: {x | x is an integer}) Page 2 Discrete Mathematics by Yang-Sae Moon

Basic Properties of Sets 1. 6 Sets are inherently unordered: (순서가 중요치 않다!) • No matter what objects a, b, and c denote, {a, b, c} = {a, c, b} = {b, a, c} = {b, c, a} = {c, a, b} = {c, b, a}. All elements are distinct (unequal); multiple listings make no difference! (중복은 의미가 없다!) • If a=b, then {a, b, c} = {a, c} = {b, c} = {a, a, b, c, c}. • This set contains at most two elements! Page 3 Discrete Mathematics by Yang-Sae Moon

Definition of Set Equality 1. 6 Sets Two sets are declared to be equal if and only if they contain exactly the same elements. (동일한 원소들로 이루어진 두 집합은 동일하다. ) In particular, it does not matter how the set is defined or denoted. (집합의 equality에서 정의나 표현은 중요치 않다. ) For example: The set {1, 2, 3, 4} = {x | x is an integer where x > 0 and x < 5 } = {x | x is a positive integer whose square is >0 and <25} Page 4 Discrete Mathematics by Yang-Sae Moon

Infinite Sets (무한 집합) 1. 6 Sets Conceptually, sets may be infinite (i. e. , not finite, without end, unending). (집합은 무한할 수 있다. 무한집합) Symbols for some special infinite sets: • N = {0, 1, 2, …} The Natural numbers. (자연수의 집합) • Z = {…, -2, -1, 0, 1, 2, …} The Zntegers. (정수의 집합) • Z+ = {1, 2, 3, …} The positive integers. (양의 정수의 집합) • Q = {p/q | p Z, q 0} The rational numbers. (유리수의 집합) • R = The Real numbers, such as 3. 141592… (실수의 집합) Infinite sets come in different sizes! (무한집합이라도 크기가 다를 수 있다. ) We will cover it in $3. 2. Page 5 Discrete Mathematics by Yang-Sae Moon
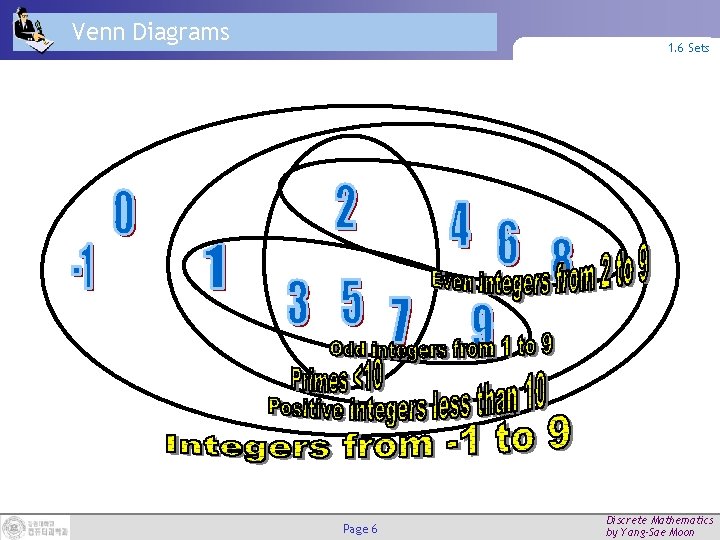
Venn Diagrams 1. 6 Sets Page 6 Discrete Mathematics by Yang-Sae Moon

원소(Elements or Members) 1. 6 Sets x S (“x is in S”) is the proposition that object x is an lement or member of set S. (x는 S의 원소이다. ) • e. g. 3 N, ‘a’ {x | x is a letter of the alphabet} • Can define set equality in terms of relation: (원소 기호를 사용한 두 집합의 동치 증명) S = T x(x S x T) x(x T x S) x(x S x T) “Two sets are equal iff they have all the same members. ” x S (x S) “x is not in S” Page 7 (x는 S의 원소가 아니다. ) Discrete Mathematics by Yang-Sae Moon
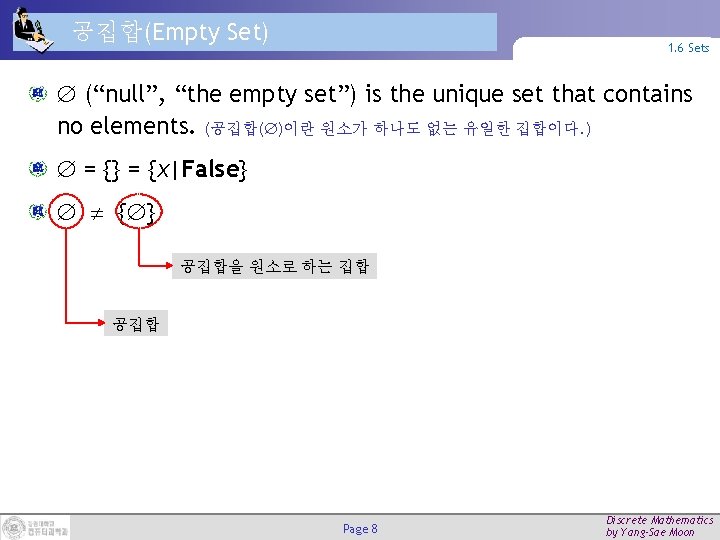
공집합(Empty Set) 1. 6 Sets (“null”, “the empty set”) is the unique set that contains no elements. (공집합( )이란 원소가 하나도 없는 유일한 집합이다. ) = {} = {x|False} { } 공집합을 원소로 하는 집합 공집합 Page 8 Discrete Mathematics by Yang-Sae Moon

Subsets(부분집합) and Supersets(모집합) 1. 6 Sets S T (“S is a subset of T”) means that every element of S is also an element of T. (S의 모든 원소는 T의 원소이다. ) S T x (x S x T) S, S S (모든 집합은 공집합과 자기 자신을 부분집합으로 가진다. ) S T (“S is a superset of T”) means T S. Note S = T (S T) S T means (S T), i. e. x(x S x T) Page 9 Discrete Mathematics by Yang-Sae Moon

Proper Subsets & Supersets 1. 6 Sets S T (“S is a proper subset of T”) means that S T but T S. Similar for S T. (S가 T에 포함되나 T는 S에 포함되지 않으면, S를 T의 진부분집합이라 한다. ) S Example: {1, 2} {1, 2, 3} T Venn Diagram equivalent of S T Page 10 Discrete Mathematics by Yang-Sae Moon
Sets are Objects, Too! 1. 6 Sets The objects that are elements of a set may themselves be sets. (집합 자체도 객체가 될 수 있고, 따라서 집합도 다른 집합의 원소가 될 수 있다. ) For example, let S={x | x {1, 2, 3}} then S={ , {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} } Note that 1 {1} {{1}} !!!! Page 11 Discrete Mathematics by Yang-Sae Moon

Cardinality and Finiteness 1. 6 Sets |S| (read “the cardinality of S”) is a measure of how many different elements S has. (|S|는 집합 S의 원소 중에서 서로 다른 값을 가지는 원소의 개수이다. ) E. g. , | |=0, |{1, 2, 3}| = 3, |{a, b}| = 2, |{{1, 2, 3}, {4, 5}}| = ____ If |S| N, then we say S is finite. Otherwise, we say S is infinite. What are some infinite sets we’ve seen? Page 12 Discrete Mathematics by Yang-Sae Moon

Power Sets (멱집합) 1. 6 Sets The power set P(S) of a set S is the set of all subsets of S. P(S) = {x | x S} (P(S)는 집합 S의 모든 부분집합을 원소로 하는 집합) Examples: • P({a, b}) = { , {a}, {b}, {a, b}}. • P( ) = { }, P({ }) = { , { }}. Sometimes P(S) is written 2 S. Note that for finite S, |P(S)| = |2 S|= 2|S|. It turns out that |P(N)| > |N|. There are different sizes of infinite sets! (자연수 집합의 power set의 크기가 자연수 집합보다 크다? !) Page 13 Discrete Mathematics by Yang-Sae Moon

Ordered n-tuples 1. 6 Sets Ordered n-tuples are like sets, except that duplicates matter, and the order makes a difference. (Ordered n-tuple에서는 원소의 중복이 허용되고, 순서도 차이를 나타낸다. ) For n N, an ordered n-tuple or a sequence of length n is written (a 1, a 2, …, an). The first element is a 1, etc. Note (1, 2) (2, 1, 1). 중복이 허용됨(의미를 가짐) 순서가 중요함(의미를 가짐) Empty sequence, singlets, pairs, triples, quadruples, …, n -tuples. Page 14 Discrete Mathematics by Yang-Sae Moon

Cartesian Products 1. 6 Sets For sets A, B, their Cartesian product A B = {(a, b) | a A b B }. (a가 A의 원소이고 b가 B의 원소인 모든 순서쌍(pair) (a, b)의 집합이다. ) E. g. {a, b} {1, 2} = {(a, 1), (a, 2), (b, 1), (b, 2)} Note that for finite A, B, |A B|=|A||B|. Note that the Cartesian product is not commutative: AB: A B=B A (Cartesian product는 교환법칙이 성립하지 않는다. ) • E. g. {a, b} {1, 2} {a, b} = {(1, a), (1, b), (2, a), (2, b)} A 1 A 2 … An = {(a 1, a 2, …, an) | ai Ai, i = 1, 2, 3, …, n} Page 15 Discrete Mathematics by Yang-Sae Moon
- Slides: 15