Introduction to Scientific Visualization with VTK November 16

Introduction to Scientific Visualization with VTK November 16 University of Chicago, CS-341 Terrence L. Disz Math and Computer Science Division Argonne National Laboratory disz@mcs. anl. gov

Visualization n Interpreting data in visual terms – Data is too complex – Too much data – Not a substitute for statistical analysis, sampling, filtering and other quantitative methods – Make use of human sensory abilities Pattern Recognition n Trend discovery n

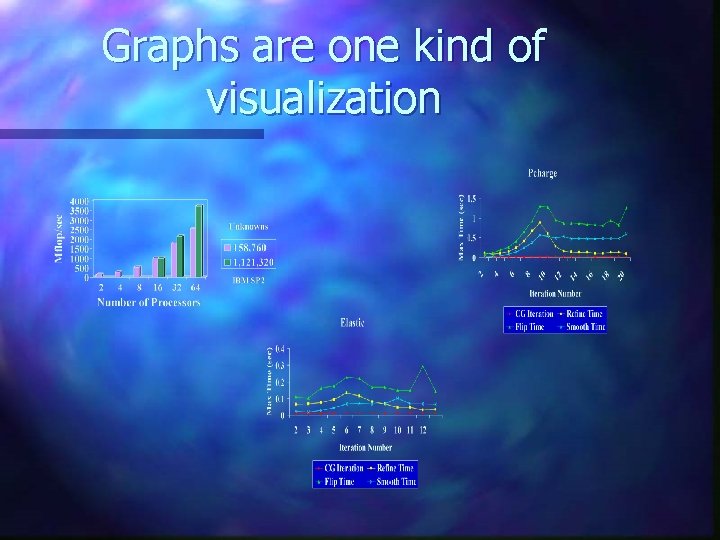
Graphs are one kind of visualization

We are interested in more complex data Multi-dimensional n Complex geometry n Computed or collected n – Simulations – MRI, CAT, etc – Microscopic to Galactic data collections

Some examples Nuclear, Quantum, and Molecular Modeling Structures, Fluids and Fields Advanced Imaging and Data Management

More Examples Surface Rendering with v. TK Volume Rendering with SGI Infinite Reality Engine

Even More Examples: Astro Physics

And, Computational Fluid Dynamics

Some Clarification Imaging n Computer Graphics n Visualization n Virtual Reality n – Stereo 3 D, Immersion, User tracking

Large Scale Virtual Reality The CAVE Immersadesk Projection Wall

Immersive Virtual Reality Visualization

Imaging, or Image Processing n Digital Image - set of discrete sample points – Picture elements (Pixel) – Gray level value – Captured or computer generated Represents a continuous function n Processing n – Edge detection, Feature extraction – Contrast enhancement – Projections, transformations

Image Processing; Edge Detection Original Image Horizontal Edges Vertical Edges Norm of the gradient http: //robotics. eecs. berkeley. edu/~mayi/imgproc/cademo. html

Computer Graphics n Creating images with a computer - Paint and draw Red Boots Tom Nast Run Run Douglas Lockyer Paper Cranes George Ho

Computer Graphics n Creating images with a computer - 3 d © 1998 Pixar Animation Studios, All Rights Reserved. www. pixar. com http: //www. websharx. com: 80/~dfarmer/gallry 1. htm

Computer Graphics n Components – Model Geometry n Surface properties n Objects or abstract volumes n – Lighting n Number, position, properties – Viewpoint – Projection

Rendering Converting graphical data into images n Visualization n – Transforms data into graphical data (primitives) n Points, triangles, etc – Graphical primitives are rendered n Image rendering, Object rendering, Volume rendering

Image Based Rendering n Painters Algorithm – Draw polygons from back to front n Scan Line – Look through each pixel to find first ploygon intersected n Z-buffer – Assign z-value to each polygon, draw closest one, pixel by pixel

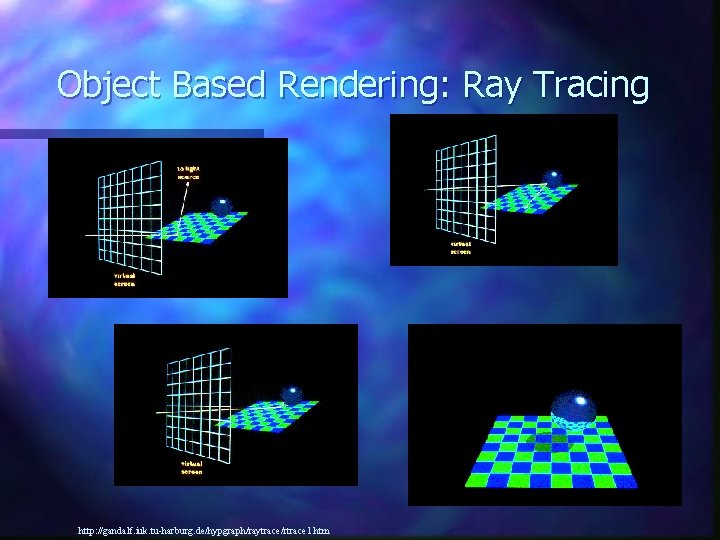
Object Based Rendering: Ray Tracing http: //gandalf. iuk. tu-harburg. de/hypgraph/raytrace/rtrace 1. htm

Volume Rendering Displays all of the 3 -D data at once, like an X-ray: Denser parts are more opaque. n User controls the density of various data values. n

Computer Graphics: Coordinate Systems n Model – local coordinate system n World – Where the models are placed n View – Logical Image Plane n Display – X, Y Pixel locations

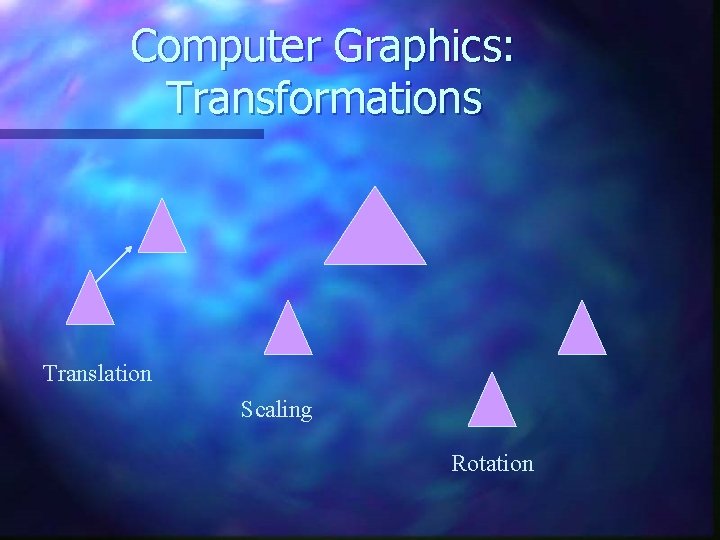
Computer Graphics: Transformations Translation Scaling Rotation

Transformation Matrix To translate the point (x, y, z) by the vector (tx, ty, tz) Transformation Matrix for Translation

Scaling, Rotation Scaling Matrix Rotate about x

Visualization is more than computer graphics Data is 3 Dimensional or greater n Data transformations occur frequently n – Feedback from vis system causes data transformations n Interactive – Exploration, discovery, understanding

Using VTK for Scientific Visualization n The Visualization. Toolkit, 2 nd edition – Schroeder, Martin, Lorenson – Prentice Hall n VTK Software – http: //www. kitware. com/vtk. html n n Software, book, FAQ’s, discussion lists, examples, etc /opt/courses/anl/vtk – graphics/examples. Cxx

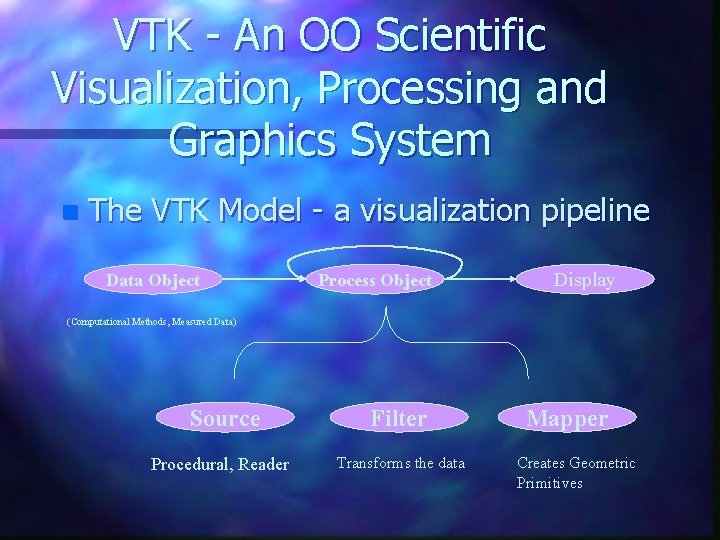
VTK - An OO Scientific Visualization, Processing and Graphics System n The VTK Model - a visualization pipeline Data Object Process Object Display (Computational Methods, Measured Data) Source Procedural, Reader Filter Transforms the data Mapper Creates Geometric Primitives

The VTK Model - A simple example Sphere Source Elevation Filter Mapper vtk. Sphere. Source *sphere = vtk. Sphere. Source: : new(); vtk. Elevation. Filter *color. It = vtk. Elevation. Filter: : New(); color. It->Set. Input(Sphere->Get. Output()); vtk. Data. Set. Mapper *mapper = vtk. Data. Set. Mapper: : New(); mapper->Set. Input(color. It->Get. Output()); vtk. Actor *actor = vtk. Actor: : New(); actor->Set. Mapper(mapper);

Data Representation - Cells & Points n Topology – Shape such as triangle, tetrahedron n Geometry – Point Coordinates assigned to a topology n Data Attributes – Data associated with topology or geometry

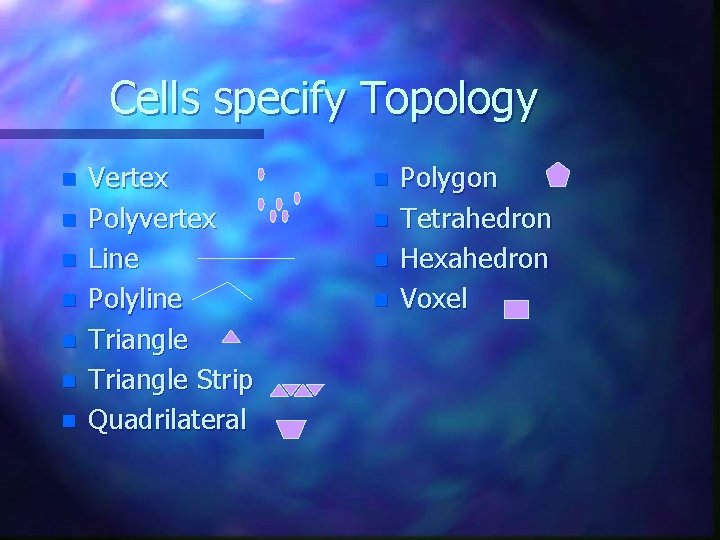
Cells specify Topology n n n n Vertex Polyvertex Line Polyline Triangle Strip Quadrilateral n n Polygon Tetrahedron Hexahedron Voxel

Cells n Cell is defined by an ordered list of points – Triangle, quadrilateral points specified counter clockwise 6 – Others 3 as shown 7 1 2 Tetrahedron 0 5 4 3 0 2 1 Hexahedron

Meshes are made of Cells n Cells can be many different shapes and sizes – e. g. in 2 D: Triangles, Quadrilaterals, etc – e. g. in 3 D Tetrahedra, Hexahedra, Pyramids, etc. n Meshes can consist of one or more types Quadrilateral of cells Prism Triangle Tetrahedron Hexahedron Mesh

VTK Dataset Types vtk. Structured. Points n vtk. Rectilinear. Grid n vtk. Structured. Grid n vtk. Poly. Data n vtk. Unstructured. Grid n Methods for reading and writing n

Datasets n Organizing structure plus attributes – Structured points – Rectilinear Grid – Structured Grid

Unstructured Grid A collection of vertices, edges, faces and cells whose connectivity information must be explicitly stored

How are unstructured meshes different than regular grids? n Regular Grids – e. g. , Cartesian grids, logically rectangular grids – mesh info accessed implicitly using grid point indices n Efficient in both computation and storage – typically use finite difference discretization n Unstructured Meshes – mesh connectivity information must be stored n Incurs memory and computational cost – handles complex geometries and grid adaptivity – typically use finite volume or finite element discretization – mesh quality becomes a concern

Data Attributes Assigned to points(VTK) or cells Scalars n Vector n – Magnitude and direction n Normal – a vector of magnitude 1 – Used for lighting n Texture Coordinate – Mapping data points into a texture space n Tensor

Visualization of Attributes n Scalar – Color Mapping – Countouring n 3 D Isosurface 1 10 4 8 Contour Value of 5

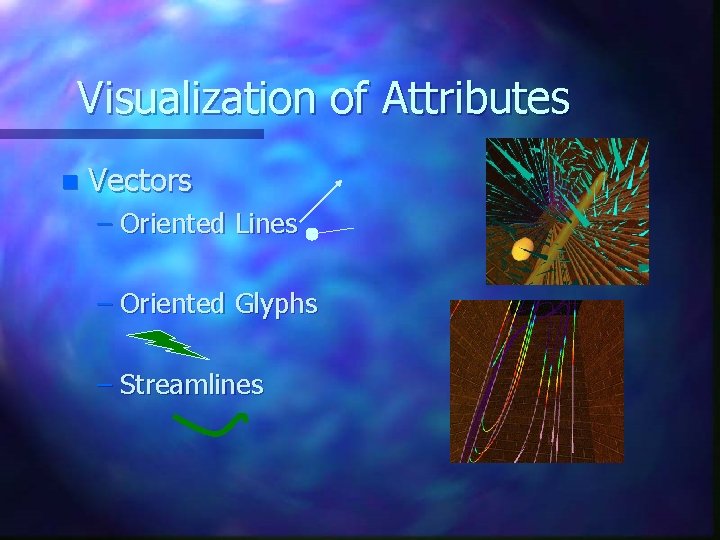
Visualization of Attributes n Vectors – Oriented Lines – Oriented Glyphs – Streamlines

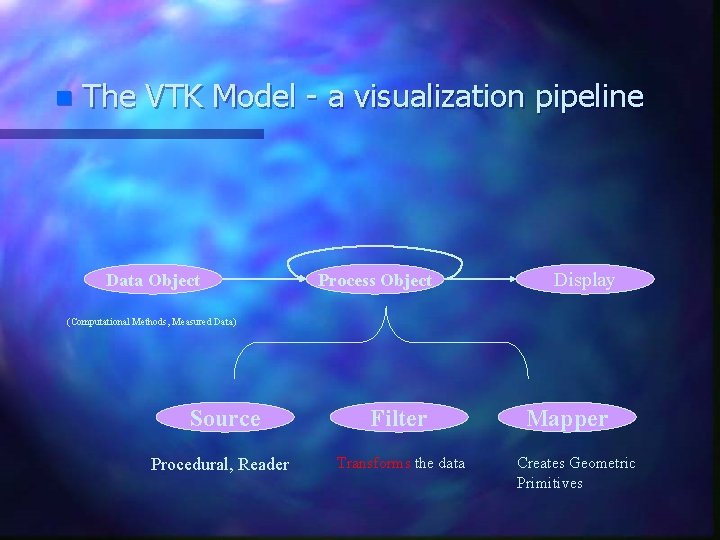
n The VTK Model - a visualization pipeline Data Object Process Object Display (Computational Methods, Measured Data) Source Procedural, Reader Filter Transforms the data Mapper Creates Geometric Primitives

Some Transformations n Decimation – Reduce polygon count, preserving topology

Some Transformations n Contouring – Create boundaries (contours) between regions n Triangulate – Create topology from unstructured points

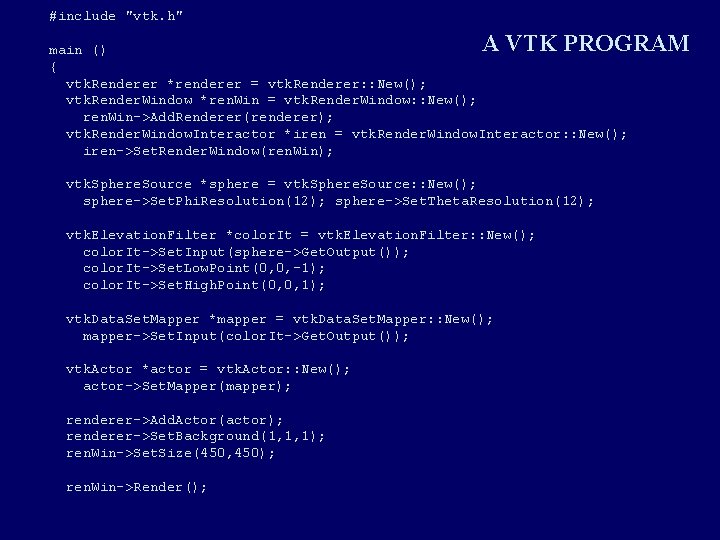
#include "vtk. h" A VTK PROGRAM main () { vtk. Renderer *renderer = vtk. Renderer: : New(); vtk. Render. Window *ren. Win = vtk. Render. Window: : New(); ren. Win->Add. Renderer(renderer); vtk. Render. Window. Interactor *iren = vtk. Render. Window. Interactor: : New(); iren->Set. Render. Window(ren. Win); vtk. Sphere. Source *sphere = vtk. Sphere. Source: : New(); sphere->Set. Phi. Resolution(12); sphere->Set. Theta. Resolution(12); vtk. Elevation. Filter *color. It = vtk. Elevation. Filter: : New(); color. It->Set. Input(sphere->Get. Output()); color. It->Set. Low. Point(0, 0, -1); color. It->Set. High. Point(0, 0, 1); vtk. Data. Set. Mapper *mapper = vtk. Data. Set. Mapper: : New(); mapper->Set. Input(color. It->Get. Output()); vtk. Actor *actor = vtk. Actor: : New(); actor->Set. Mapper(mapper); renderer->Add. Actor(actor); renderer->Set. Background(1, 1, 1); ren. Win->Set. Size(450, 450); ren. Win->Render();

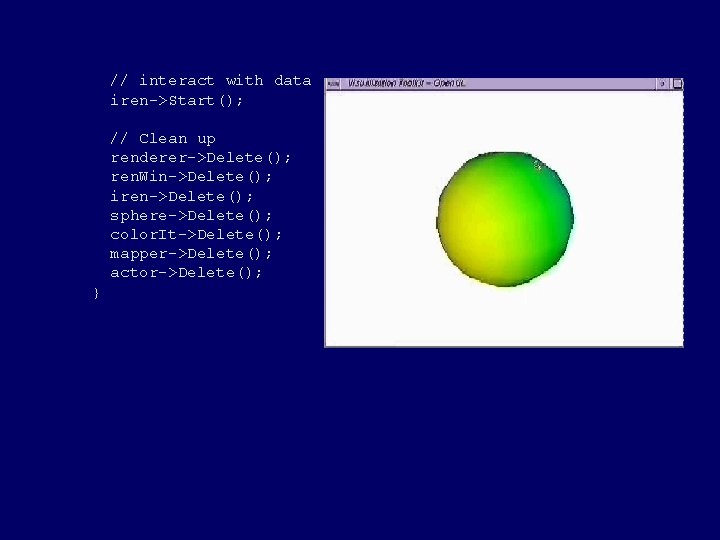
// interact with data iren->Start(); // Clean up renderer->Delete(); ren. Win->Delete(); iren->Delete(); sphere->Delete(); color. It->Delete(); mapper->Delete(); actor->Delete(); }

Your Assignment n Use output from the 11/2 assignment or use our data – sol. 22. 22. out n Compile and run the converter program to transform the data into a vtk dataset – converter sol. 22. 22. out 22 22 22 n Compile and Run the supplied VTK vis program on the data – Sample. C

Your Assignment Make more runs, modifying the thresholds n Add a third cutting plane and rerun your test data n Write a short report explaining what happened n

The Output

Assignment Resource Location n ~disz/assignment – Sample data – makefile – converter program – Vis app