Introduction to ROBOTICS Velocity Analysis Jacobian University of

Introduction to ROBOTICS Velocity Analysis Jacobian University of Bridgeport 1

Kinematic relations X=FK(θ) θ =IK(X) Joint Space Task Space Location of the tool can be specified using a joint space or a cartesian space description

Velocity relations • Relation between joint velocity and cartesian velocity. • JACOBIAN matrix J(θ) Joint Space Task Space

Jacobian • Suppose a position and orientation vector of a manipulator is a function of 6 joint variables: (from forward kinematics) X = h(q)

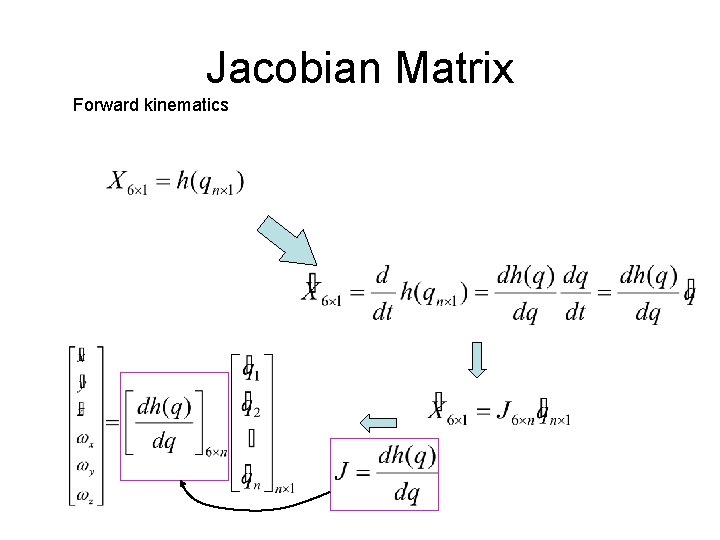
Jacobian Matrix Forward kinematics

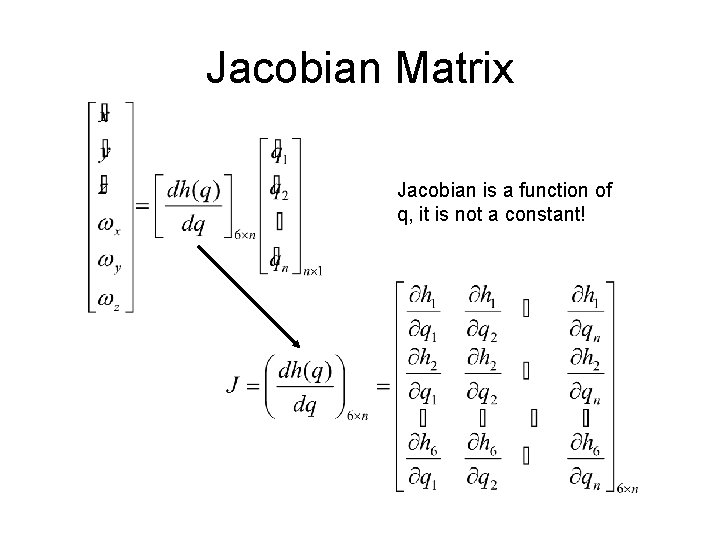
Jacobian Matrix Jacobian is a function of q, it is not a constant!

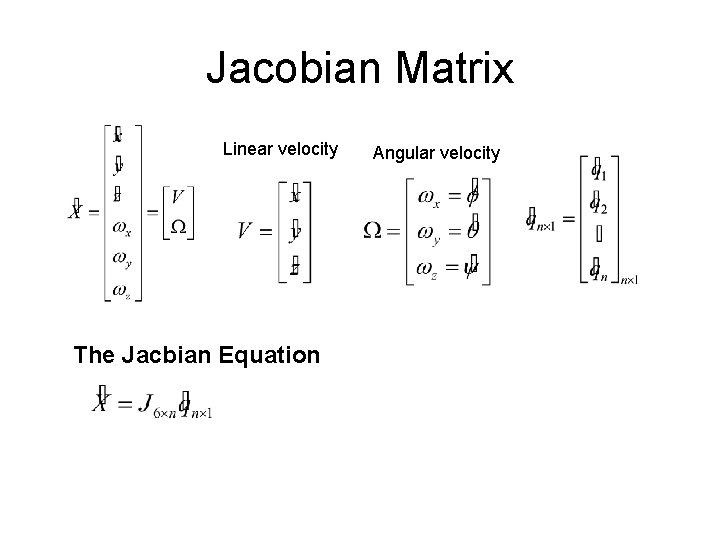
Jacobian Matrix Linear velocity The Jacbian Equation Angular velocity

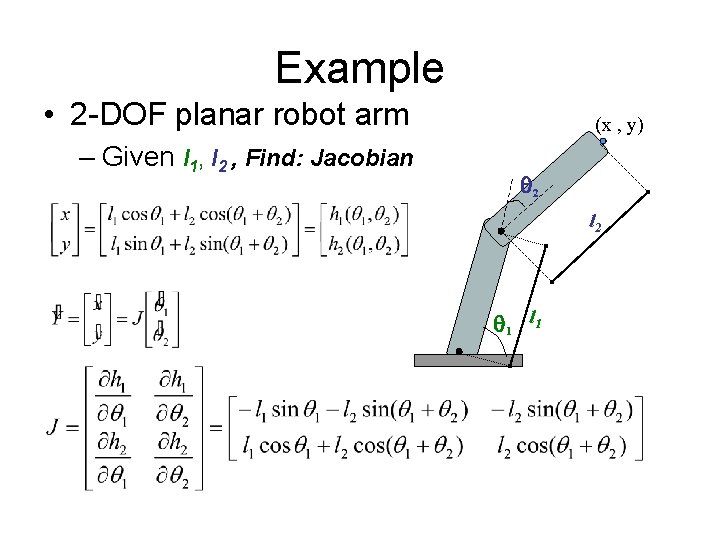
Example • 2 -DOF planar robot arm – Given l 1, l 2 , Find: Jacobian (x , y) 2 l 2 1 l 1

Singularities • The inverse of the jacobian matrix cannot be calculated when det [J(θ)] = 0 • Singular points are such values of θ that cause the determinant of the Jacobian to be zero

• Find the singularity configuration of the 2 -DOF planar robot arm determinant(J)=0 Not full rank V l 2 Y 2 =0 Det(J)=0 1 l 1 x (x , y)

Jacobian Matrix • Pseudoinverse – Let A be an mxn matrix, and let be the pseudoinverse of A. If A is of full rank, then can be computed as:

Jacobian Matrix – Example: Find X s. t. Matlab Command: pinv(A) to calculate A+

Jacobian Matrix • Inverse Jacobian • Singularity – rank(J)<n : Jacobian Matrix is less than full rank – Jacobian is non-invertable – Boundary Singularities: occur when the tool tip is on the surface of the work envelop. – Interior Singularities: occur inside the work envelope when two or more of the axes of the robot form a straight line, i. e. , collinear

Singularity • At Singularities: – the manipulator end effector cant move in certain directions. – Bounded End-Effector velocities may correspond to unbounded joint velocities. – Bounded joint torques may correspond to unbounded End-Effector forces and torques.

Jacobian Matrix • If • Then the cross product

Remember DH parmeter • The transformation matrix T

Jacobian Matrix

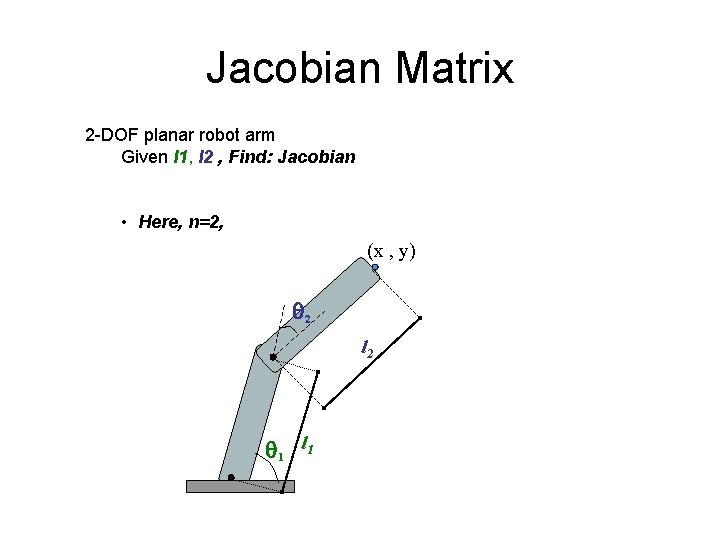
Jacobian Matrix 2 -DOF planar robot arm Given l 1, l 2 , Find: Jacobian • Here, n=2, (x , y) 2 l 2 1 l 1

Where (θ 1 + θ 2 ) denoted by θ 12 and 19

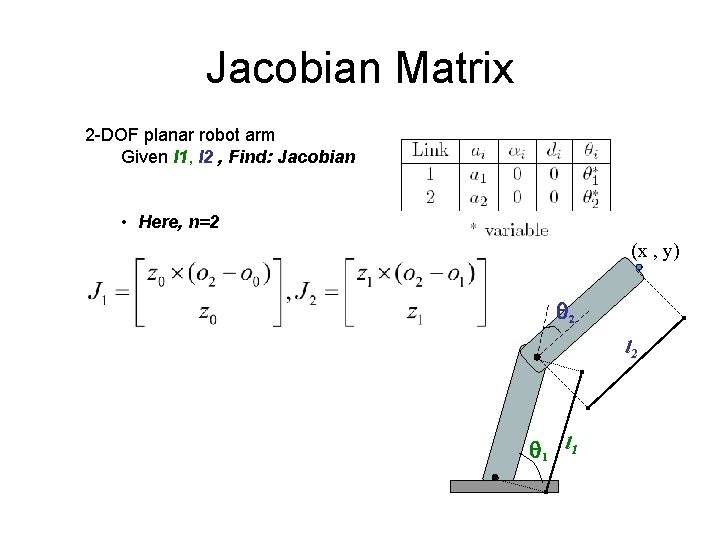
Jacobian Matrix 2 -DOF planar robot arm Given l 1, l 2 , Find: Jacobian • Here, n=2 (x , y) 2 l 2 1 l 1

Jacobian Matrix

Jacobian Matrix

Jacobian Matrix The required Jacobian matrix J

Stanford Manipulator The DH parameters are:

Stanford Manipulator

Stanford Manipulator T 4 = [ c 1 c 2 c 4 -s 1 s 4, -c 1 s 2, -c 1 c 2 s 4 -s 1*c 4, c 1 s 2 d 3 -sin 1 d 2] [ s 1 c 2 c 4+c 1 s 4, -s 1 s 2, -s 1 c 2 s 4+c 1 c 4, s 1 s 2 d 3+c 1*d 2] [-s 2 c 4, -c 2, s 2 s 4, c 2*d 3] [ 0, 0, 0, 1]

Stanford Manipulator T 5 = [ (c 1 c 2 c 4 -s 1 s 4)c 5 -c 1 s 2 s 5, c 1 c 2 s 4+s 1 c 4, (c 1 c 2 c 4 -s 1 s 4)s 5+c 1 s 2 c 5, c 1 s 2 d 3 -s 1 d 2] [ (s 1 c 2 c 4+c 1 s 4)c 5 -s 1 s 2 s 5, s 1 c 2 s 4 -c 1 c 4, (s 1 c 2 c 4+c 1 s 4)s 5+s 1 s 2 c 5, s 1 s 2 d 3+c 1 d 2] [ -s 2 c 4 c 5 -c 2 s 5, -s 2 s 4, -s 2 c 4 s 5+c 2 c 5, c 2 d 3] [ 0, 0, 0, 1]

Stanford Manipulator T 5 = [ (c 1 c 2 c 4 -s 1 s 4)c 5 -c 1 s 2 s 5, c 1 c 2 s 4+s 1 c 4, (c 1 c 2 c 4 -s 1 s 4)s 5+c 1 s 2 c 5, c 1 s 2 d 3 -s 1 d 2] [ (s 1 c 2 c 4+c 1 s 4)c 5 -s 1 s 2 s 5, s 1 c 2 s 4 -c 1 c 4, (s 1 c 2 c 4+c 1 s 4)s 5+s 1 s 2 c 5, s 1 s 2 d 3+c 1 d 2] [ -s 2 c 4 c 5 -c 2 s 5, -s 2 s 4, -s 2 c 4 s 5+c 2 c 5, c 2 d 3] [ 0, 0, 0, 1]

Stanford Manipulator T 6 = [ c 6 c 5 c 1 c 2 c 4 -c 6 c 5 s 1 s 4 -c 6 c 1 s 2 s 5+s 6 c 1 c 2 s 4+s 6 s 1 c 4, c 5 c 1 c 2 c 4+s 6 c 5 s 1 s 4+s 6 c 1 s 2 s 5+c 6 c 1 c 2 s 4+c 6 s 1 c 4, s 5 c 1 c 2 c 4 -s 5 s 1 s 4+c 1 s 2 c 5, d 6 s 5 c 1 c 2 c 4 -d 6 s 5 s 1 s 4+d 6 c 1 s 2 c 5+c 1 s 2 d 3 -s 1 d 2] [ c 6 c 5 s 1 c 2 c 4+c 6 c 5 c 1 s 4 -c 6 s 1 s 2 s 5+s 6 s 1 c 2 s 4 -s 6 c 1 c 4, -s 6 c 5 s 1 c 2 c 4 s 6 c 5 c 1 s 4+s 6 s 1 s 2 s 5+c 6 s 1 c 2 s 4 -c 6 c 1 c 4, s 5 s 1 c 2 c 4+s 5 c 1 s 4+s 1 s 2 c 5, d 6 s 5 s 1 c 2 c 4+d 6 s 5 c 1 s 4+d 6 s 1 s 2 c 5+s 1 s 2 d 3+c 1 d 2] [ -c 6 s 2 c 4 c 5 -c 6 c 2 s 5 -s 2 s 4 s 6, s 6 s 2 c 4 c 5+s 6 c 2 s 5 -s 2 s 4 c 6, -s 2 c 4 s 5+c 2 c 5, d 6 s 2 c 4 s 5+d 6 c 2 c 5+c 2 d 3] [ 0, 0, 0, 1]

Stanford Manipulator Joints 1, 2 are revolute Joint 3 is prismatic The required Jacobian matrix J

Inverse Velocity – The relation between the joint and end-effector velocities: where j (m×n). If J is a square matrix (m=n), the joint velocities: – If m<n, let pseudoinverse J+ where

Acceleration – The relation between the joint and end-effector velocities: – Differentiating this equation yields an expression for the acceleration: – Given of the end-effector acceleration, the joint acceleration