Introduction to Regression Lecture 2 1 1 Review

Introduction to Regression Lecture 2. 1 1. Review of Lecture 1. 1 2. Correlation 3. Pitfalls with Regression and Correlation 4. Introducing Multiple Linear Regression – Job times case study – Stamp sales case study 5. Homework Diploma in Statistics Introduction to Regression 1

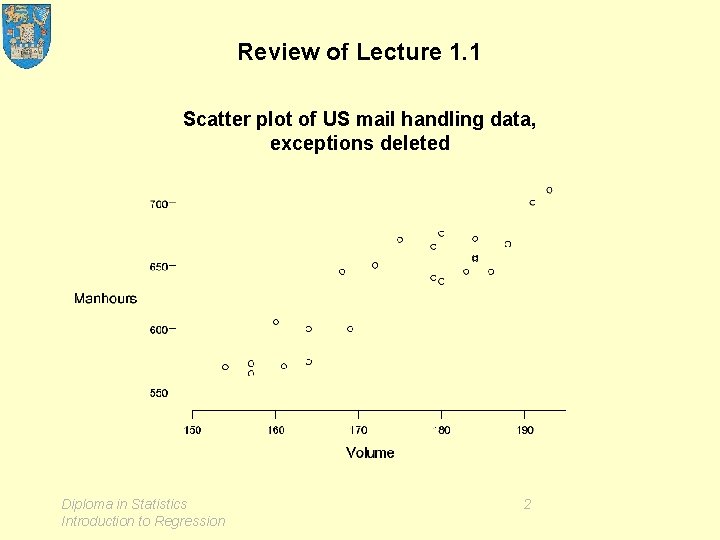
Review of Lecture 1. 1 Scatter plot of US mail handling data, exceptions deleted Diploma in Statistics Introduction to Regression 2

Always look ar your data! "Although regression can be done without ever looking at a scatter plot, that is the statistical equivalent of flying blind" Amy Lap Mui Choi, JF MSISS, 1993/94. "Decision-making under risk is when you know what will probably happen and decision-making under uncertainty is when you probably know what will happen. " Anon. , JF MSISS 1995/96 Diploma in Statistics Introduction to Regression 3

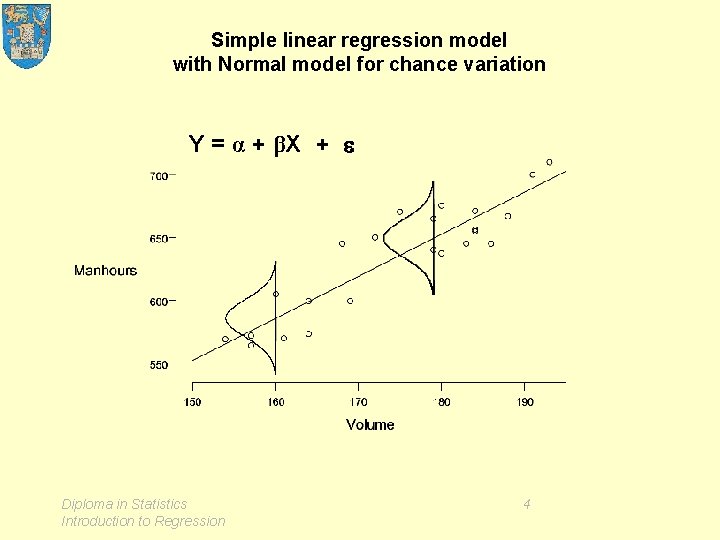
Simple linear regression model with Normal model for chance variation Y = α + βX + Diploma in Statistics Introduction to Regression 4

The prediction formula Prediction equation: Prediction equation allowing for chance variation: Diploma in Statistics Introduction to Regression 5

Homework Use the prediction formula to predict the extra manpower requirement during Christmas period, based on the experience of Period 7, Fiscal 1963, when Y was 1, 070 and X was 270. Compare with actual. Comment. Diploma in Statistics Introduction to Regression 6

Application 1 Confidence interval for marginal change Recall confidence interval for m: or Confidence interval for b: Small sample: Diploma in Statistics Introduction to Regression 7

Diploma in Statistics Introduction to Regression 8

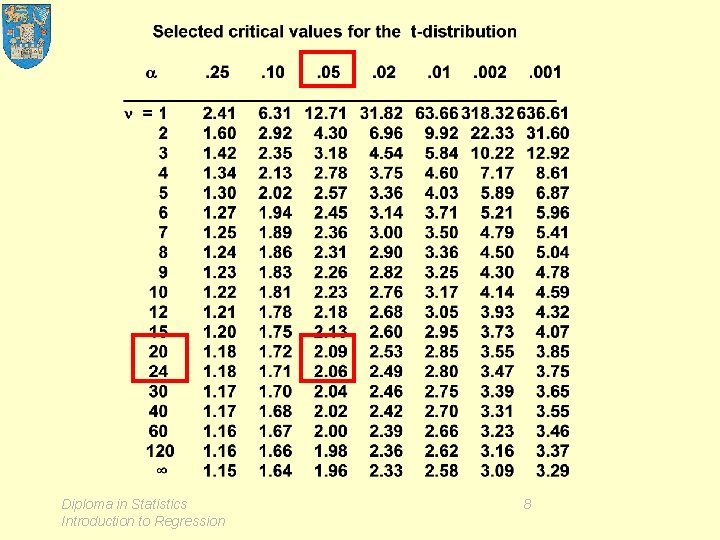
Application 2 Testing the statistical significance of the intercept Formal test: H 0: a=0 Test statistic: Critical value: 2. 08) 2 (or t 21, . 05 = Z < 2 (or t < 2. 08) Calculated value: 0. 848 Comparison: Conclusion: Diploma in Statistics Introduction to Regression Accept H 0 9

Testing the statistical significance of the intercept Informal test: is less than its standard error, Draw a picture! Diploma in Statistics Introduction to Regression 10

More on Minitab results Regression Analysis: Manhours versus Volume The regression equation is Manhours = 50. 4 + 3. 35 Volume Predictor Constant Volume Coef 50. 44 3. 3454 SE Coef 59. 46 0. 3401 T 0. 85 9. 84 S = 18. 9300 Diploma in Statistics Introduction to Regression 11 P 0. 406 0. 000

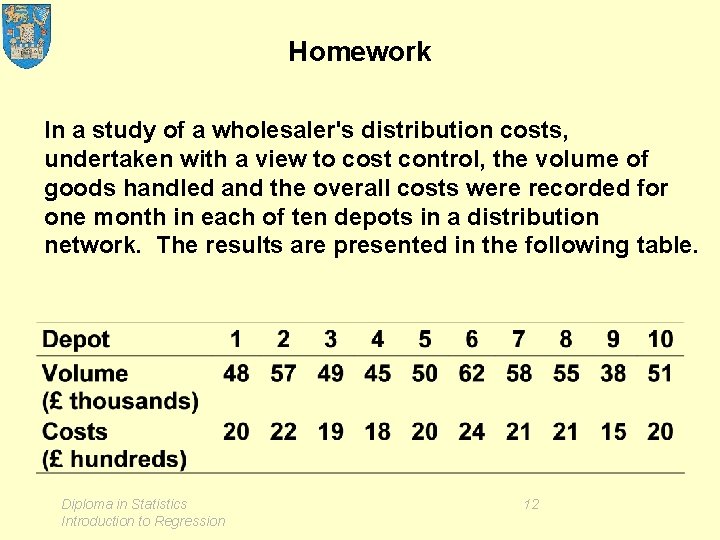
Homework In a study of a wholesaler's distribution costs, undertaken with a view to cost control, the volume of goods handled and the overall costs were recorded for one month in each of ten depots in a distribution network. The results are presented in the following table. Diploma in Statistics Introduction to Regression 12

Homework The simple linear regression of costs (Y) on volume (X) was calculated, and resulted in the following numerical summary. Regression Analysis: Costs versus Volume The regression equation is Costs = 2. 98 + 0. 332 Volume Predictor Constant Volume Coef 2. 982 0. 33174 SE Coef 1. 646 0. 03182 T 1. 81 10. 42 S = 0. 667603 Diploma in Statistics Introduction to Regression 13 P 0. 108 0. 000

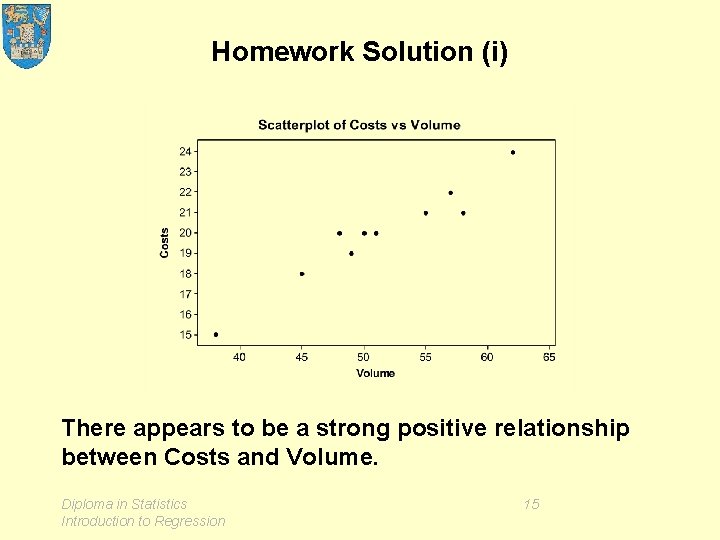
Homework (i) Draw a scatter plot for these data. Comment. Interpret the numerical summary in context. (ii) Calculate a prediction interval for costs next month when Volume in Depot 1 is planned to be £ 40, 000, and Volume in Depot 2 is planned to be £ 51, 000. (iii) Next month, when the two depots recorded volumes of £ 40, 000 and £ 51, 000 as planned, costs were £ 1, 700 and £ 2, 300 respectively. Comment on each case. Illustrate with an enhancement of your scatter plot. Diploma in Statistics Introduction to Regression 14

Homework Solution (i) There appears to be a strong positive relationship between Costs and Volume. Diploma in Statistics Introduction to Regression 15

Homework Solution (i) Costs increase approximately linearly with Volume, by around £ 33. 20 for every £ 1, 000 increase in Volume, from a base of around £ 300. (Costs = 2. 98 + 0. 332 Volume) The cost for a given volume is subject to chance variation with a standard deviation of around £ 67. (S = 0. 667603) Diploma in Statistics Introduction to Regression 16

Homework Solution (ii) Volume = £ 40, 000, Costs (£ 1, 491 , £ 1, 759) Volume = £ 51, 000, Costs (£ 1, 857 , £ 2, 124) (iii) £ 1, 700 is within the corresponding prediction interval, satisfactory. £ 2, 300 is outside the corresponding prediction interval, too high. An investigation is needed. Illustrate Diploma in Statistics Introduction to Regression 17

More precise formulas Prediction interval for next response: (ii) Volume = £ 40, 000, Costs (£ 1, 444 , £ 1, 807) Volume = £ 51, 000, Costs (£ 1, 829 , £ 2, 151) Confidence interval for mean response: Diploma in Statistics Introduction to Regression 18

Standard error • of prediction • of estimation Ref: "The Standard Error of Prediction" Extra Notes folder in mstuart/get or Diploma webpage Diploma in Statistics Introduction to Regression 19

Homework Solution Diploma in Statistics Introduction to Regression 20

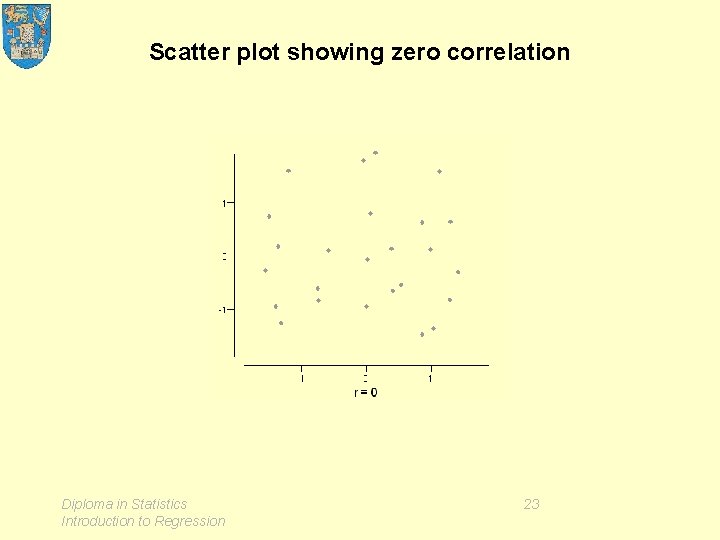
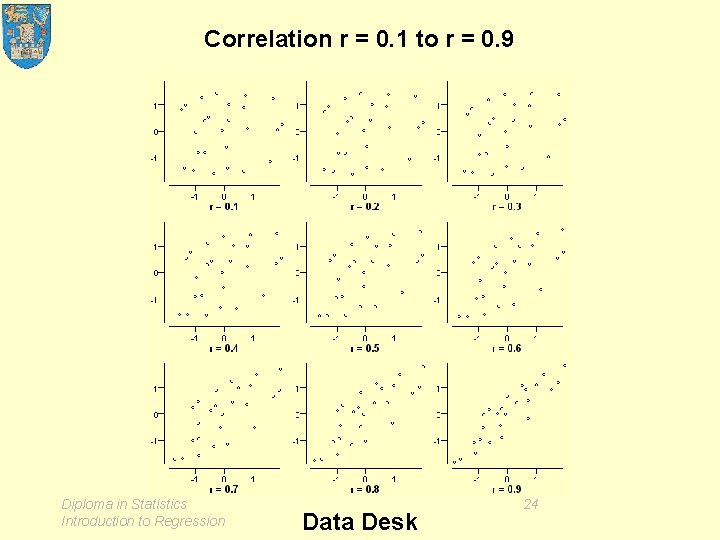
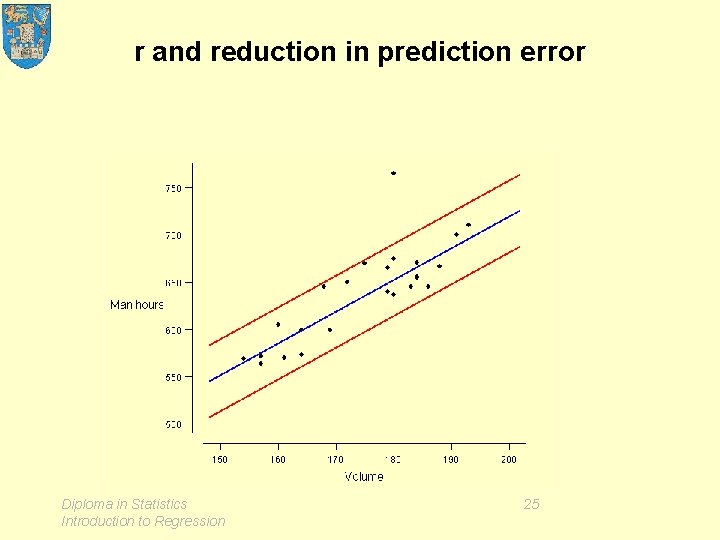
2. Correlation • The correlation coefficient formula • r and reduction of prediction error • Positive and negative correlation • Perfect correlation • Conventional interpretations of r Diploma in Statistics Introduction to Regression 21

The correlation coefficient formula Recall equivalently, Diploma in Statistics Introduction to Regression 22

Scatter plot showing zero correlation Diploma in Statistics Introduction to Regression 23

Correlation r = 0. 1 to r = 0. 9 Diploma in Statistics Introduction to Regression Data Desk 24

r and reduction in prediction error Diploma in Statistics Introduction to Regression 25

r and reduction in prediction error Diploma in Statistics Introduction to Regression 26

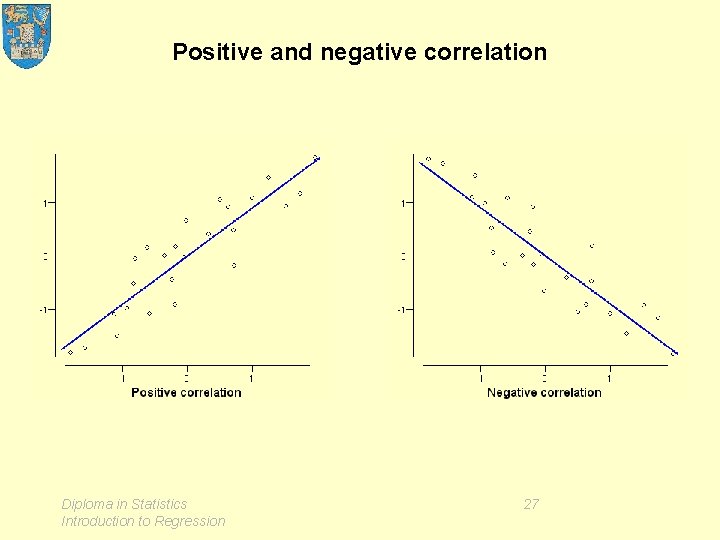
Positive and negative correlation Diploma in Statistics Introduction to Regression 27

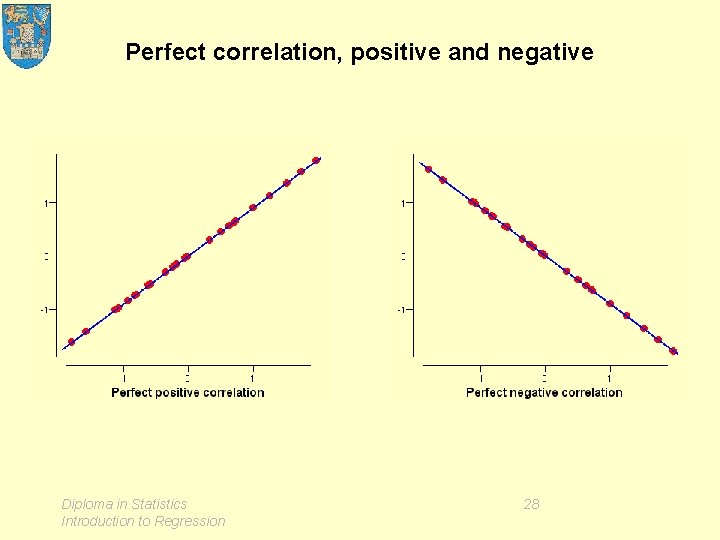
Perfect correlation, positive and negative Diploma in Statistics Introduction to Regression 28

Conventional interpretations of r Science / Engineering: Econometrics: otherwise, Sociology: r > 0. 9 is "interesting" r > 0. 7 is "interesting", r > 0. 5 is "interesting" r > 0. 3 is "interesting" Recommendation: compare s to SY Diploma in Statistics Introduction to Regression 29

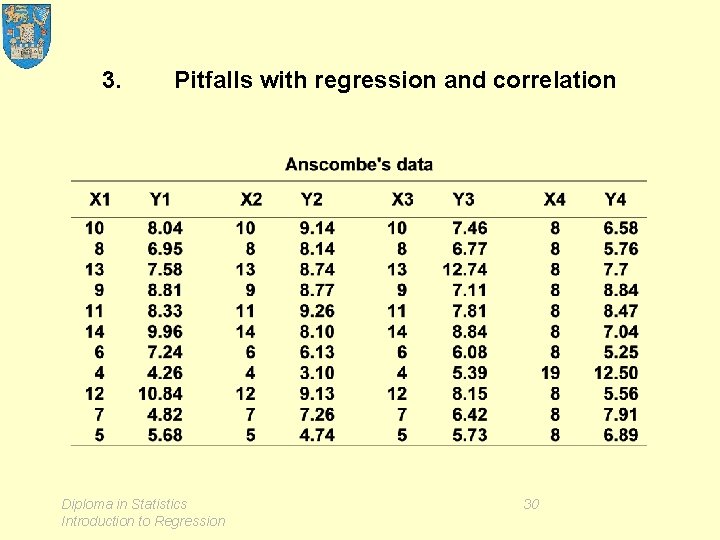
3. Pitfalls with regression and correlation Diploma in Statistics Introduction to Regression 30

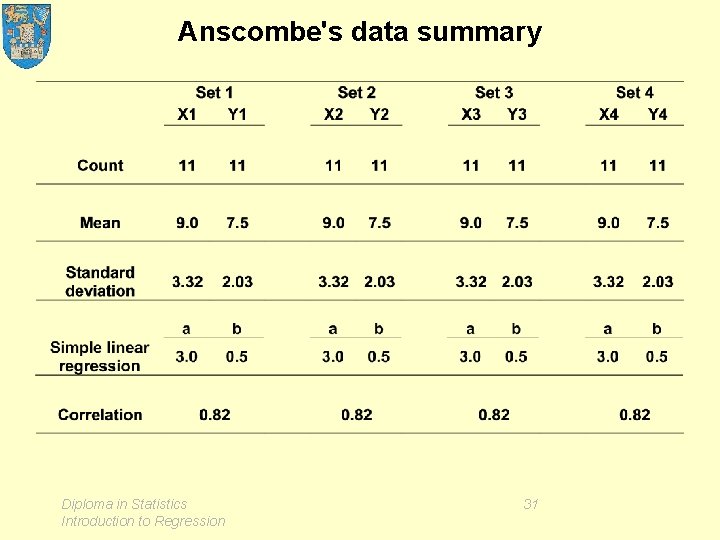
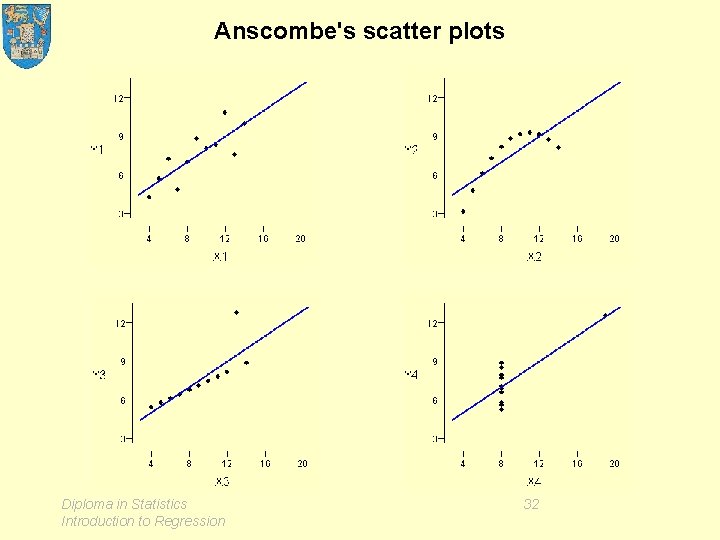
Anscombe's data summary Diploma in Statistics Introduction to Regression 31

Anscombe's scatter plots Diploma in Statistics Introduction to Regression 32

Homework The shelf life of packaged foods depends on many factors. Dry cereal (such as corn flakes) is considered to be a moisture-sensitive product, with the shelf life determined primarily by moisture. In a study of the shelf life of one brand of cereal, packets of cereal were stored in controlled conditions (23°C and 50% relative humidity) for a range of times, and moisture content was measured. The results were as follows. Draw a scatter diagram. Comment. What action is suggested? Why? Diploma in Statistics Introduction to Regression 33

Following appropriate action, the following regression was computed. The regression equation is Moisture Content = 2. 86 + 0. 0417 Storage Time Predictor Constant Storage Time Coef 2. 86122 0. 041660 SE Coef 0. 02488 0. 001177 T 115. 01 35. 40 P 0. 000 S = 0. 0493475 Calculate a 95% confidence interval for the daily change in moisture content; show details. Diploma in Statistics Introduction to Regression 34

Was the action you suggested on studying the scatter diagram in part (a) justified? Explain. Predict the moisture content of a packet of cereal stored under these conditions for 3 weeks; calculate a prediction interval. What would be the effect on your interval of not taking the action you suggested on studying the scatter diagram? Why? Taste tests indicate that this brand of cereal is unacceptably soggy when the moisture content exceeds 4. Based on your prediction interval, do you think that a box of cereal that has been on the shelf for 3 weeks will be acceptable? Explain. What about 4 weeks? 5 weeks? What is acceptable? Diploma in Statistics Introduction to Regression 35

Reading SA Sections 6. 4, 6. 5 Diploma in Statistics Introduction to Regression 36

4 Introducing Multiple Linear Regression • SLR explaining variation in Y in terms of variation in X • MLR explaining variation in Y in terms of variation in several X 's Diploma in Statistics Introduction to Regression 37

Example 1 What determines the taste of mature cheese? • X 1 = Acetic Acid • X 2 = Hydrogen Sulphide • X 3 = Lactic Acid • Y = Taste Score Diploma in Statistics Introduction to Regression 38

Example 2 Explaining crime rates Variable Description M So Ed Po 1 Po 2 LF M. F Pop NW U 1 U 2 GDP Ineq Prob Time percentage of males aged 14– 24 indicator variable for a southern state mean years of schooling police expenditure in 1960 police expenditure in 1959 labour force participation rate number of males per 1000 females state population number of nonwhites per 1000 people unemployment rate of urban males 14– 24 unemployment rate of urban males 35– 39 gross domestic product per head income inequality probability of imprisonment average time served in state prisons Crime Diploma in Statistics population rate of crimes in a particular category per head of Introduction to Regression 39

Example 3 Estimating tree volume / timber yield For a sample of 31 black cherry trees in the Allegheny National Forest, Pennsylvania, measure • Y = volume (cubic feet), • X 1 = height (feet) • X 2 = diameter (inches) (at 54 inches above ground Diploma in Statistics Introduction to Regression 40

Example 4 The Stamp Sales Case Study The problem • January 1984, An Post established • New business plan; sales forecasts required • Historical sales data available bring in a consultant! Diploma in Statistics Introduction to Regression 41

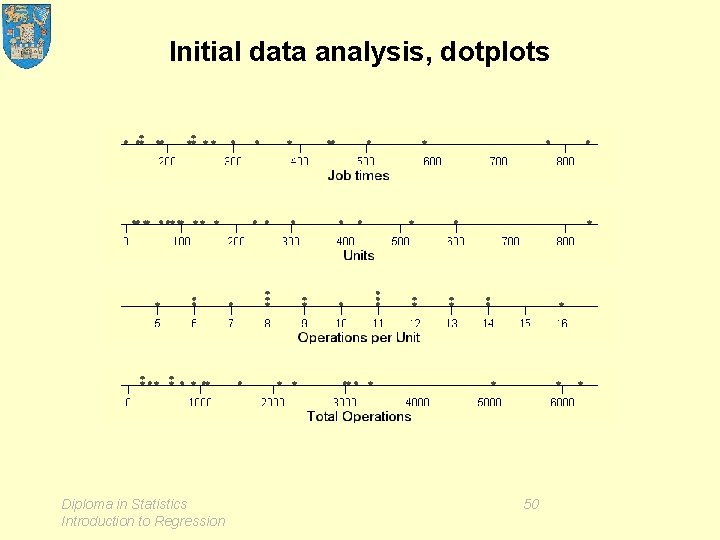
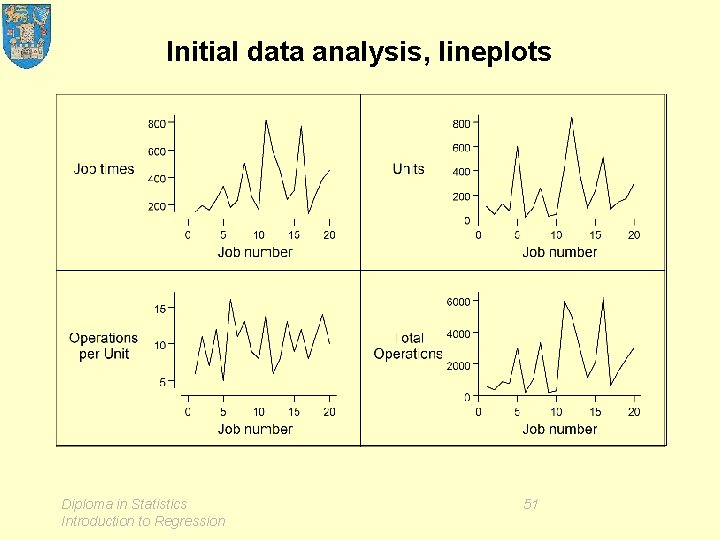
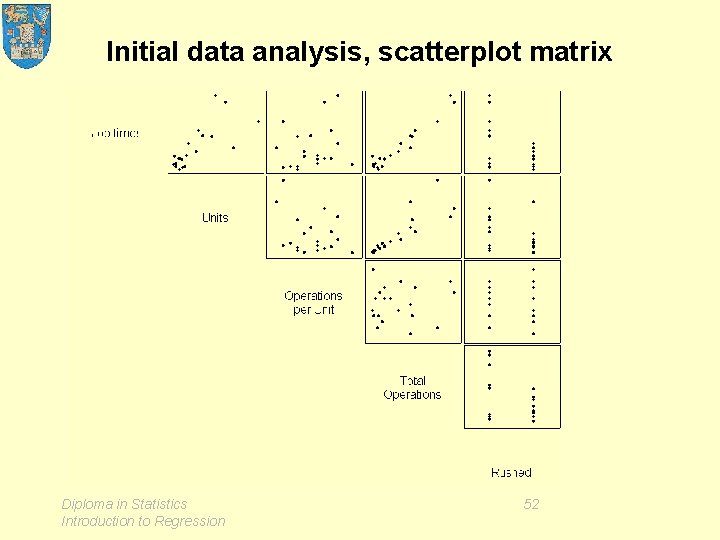
Example 5 A production prediction problem • The problem • The data • Initial data analysis – dotplots – lineplots (time series plots) – scatterplot matrix • Model fitting / estimation • Model criticism • Application Diploma in Statistics Introduction to Regression 42

Erie Metal Products: The problem Metal products fabrication: customers order varying quantities of products of varying complexity; customers demand accurate and precise order delivery times. Diploma in Statistics Introduction to Regression 43

Stephan Clark Metal Products A specially designed cabinet Diploma in Statistics Introduction to Regression Rear view 44

Stephan Clark Metal Products Instrument casing Diploma in Statistics Introduction to Regression Another view 45

Stephan Clark Metal Products Instrument casing; oblique view Diploma in Statistics Introduction to Regression Lockers 46

Stephan Clark Metal Products • "One customer is an international manufacturer of petrochemical equipment. " • "Stephen Clark supplies painted metalwork components, panels and fabrications, which are used throughout the customer's product range. " • "Stephen Clark plays an important part in them being able to cope with frequent scheduling changes. " • "Through careful program management, we are able to offer excellent flexibility of supply, delivering finished product against weekly call-offs. " Diploma in Statistics Introduction to Regression 47

Erie Metal Products: The data Diploma in Statistics Introduction to Regression 48

The variables • Response: – Jobtime, time (hours) to complete an order • Explanatory: – Units, the number of units ordered – Operations per Unit, the number of operations involved in manufacturing a unit, – Rushed, indicator of "rushed" priority status – Total Operations Diploma in Statistics Introduction to Regression Units × Operations per Unit 49

Initial data analysis, dotplots Diploma in Statistics Introduction to Regression 50

Initial data analysis, lineplots Diploma in Statistics Introduction to Regression 51

Initial data analysis, scatterplot matrix Diploma in Statistics Introduction to Regression 52

The multiple linear regression model Jobtime = a + b. Units × Units + b. Ops + b. T_Ops × T_Ops + b. Rushed × Rushed + Diploma in Statistics Introduction to Regression × Ops 53

Model parameters The regression coefficients: a, b. Units, b. Ops, b. T_Ops, b. Rushed The "uncertainty" parameter: s = standard deviation of Diploma in Statistics Introduction to Regression 54

Parameter estimates Prediction formula Jobtime = 44 – 0. 07×Units + 9. 8×Ops + 0. 1×T_Ops – 38×Rushed ± 15 Exercise Job 9, a rushed job with 21 units and 9 operations per unit, took 260 hours to complete. Was this reasonable? Diploma in Statistics Introduction to Regression 55

Choosing values for the regression coefficients, SLR Find values for a and b that minimise the deviations Y 1 − a − b. X 1, Y 2 − a − b. X 2, Y 3 − a − b. X 3, Yn − a − b. Xn Diploma in Statistics Introduction to Regression 56

The method of least squares, SLR Find values for a and b that minimise the sum of the squared deviations: (Y 1 − a − b. X 1)2 + (Y 2 − a − b. X 2)2 + (Y 3 − a − b. X 3)2 + (Yn − a − b. Xn)2 Diploma in Statistics Introduction to Regression 57

The method of least squares, MLR Find values for a and b that minimise the sum of the squared deviations: (Y 1 − a − b 1 X 11− b 2 X 21− b 3 X 31 − etc. )2 + (Y 2 − a − b 1 X 12− b 2 X 22− b 3 X 32 − etc. )2 + (Y 3 − a − b 1 X 13− b 2 X 23− b 3 X 33 − etc. )2 + (Yn − a − b 1 X 1 n− b 2 X 2 n− b 3 X 3 n − Minitab! Diploma in Statistics Introduction to Regression 58

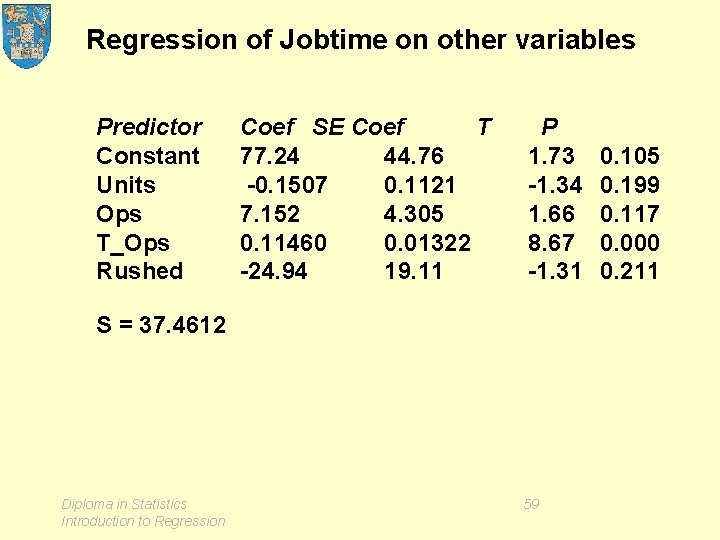
Regression of Jobtime on other variables Predictor Constant Units Ops T_Ops Rushed Coef SE Coef T 77. 24 44. 76 -0. 1507 0. 1121 7. 152 4. 305 0. 11460 0. 01322 -24. 94 19. 11 P 1. 73 -1. 34 1. 66 8. 67 -1. 31 S = 37. 4612 Diploma in Statistics Introduction to Regression 59 0. 105 0. 199 0. 117 0. 000 0. 211

Exercise From the computer output, write down the parameter estimates and the prediction formula. Predict job times for a typical job, say 300 units requiring 10 operations per unit, both normal and rushed. Diploma in Statistics Introduction to Regression 60

Exercise (continued) Is this a useful prediction? What is S? What is 2 S? When will my order arrive? NEXT Diagnostics; analysis of residuals Diploma in Statistics Introduction to Regression 61

Homework Predict job times for small (U=100, O=5), medium (U=300, O=10) and large (U=500, O=15) jobs, both normal and rushed. Present the results in tabular form. Diploma in Statistics Introduction to Regression 62

Return to The Stamp Sales Case Study The problem • January 1984, An Post established • New business plan; sales forecasts required • Historical sales data available bring in a consultant! Diploma in Statistics Introduction to Regression 63

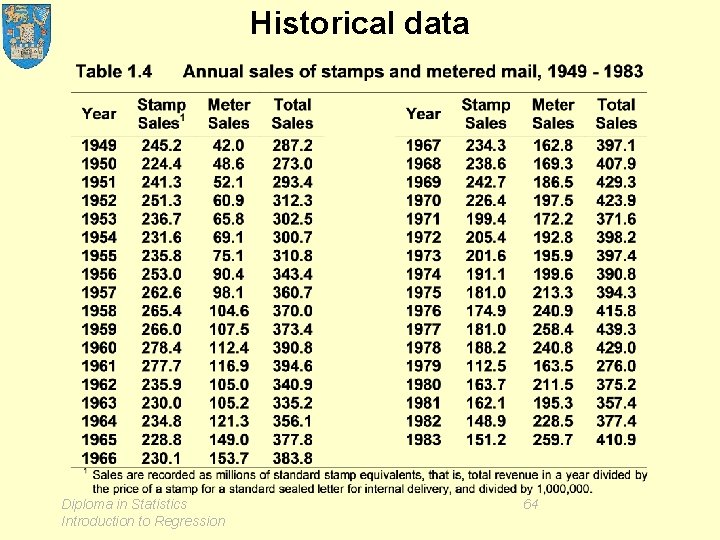
Historical data Diploma in Statistics Introduction to Regression 64

Trend projection? Diploma in Statistics Introduction to Regression 65

Factors influencing sales • Economic growth • Stamp prices • Alternative product prices measurement problems! Diploma in Statistics Introduction to Regression 66

Project: develop a sales forecasting system for An Post Terms of reference 1. Identify and collect the relevant macroeconomic data. 2. Establish a data base containing the data needed for model building; 3. Identify, estimate and check a dynamic regression model suitable for the purposes outlined below: Diploma in Statistics Introduction to Regression 67

(a) medium-term (one to five years) forecasting of aggregate demand for postal services; (b) analysis of the effects of levels of general economic activity, postal prices and the prices of competing services, on aggregate demand for postal services; (c) use as a benchmark for the analysis of the effects of demand stimulation activities. Diploma in Statistics Introduction to Regression 68

Project: develop a sales forecasting system for An Post Terms of reference 1. Identify and collect the relevant macroeconomic data. 2. Establish a data base containing the data needed for model building; 3. Identify, estimate and check a dynamic regression model suitable for the purposes outlined below: Diploma in Statistics Introduction to Regression 69

(a) medium-term (one to five years) forecasting of aggregate demand for postal services; (b) analysis of the effects of levels of general economic activity, postal prices and the prices of competing services, on aggregate demand for postal services; (c) use as a benchmark for the analysis of the effects of demand stimulation activities. Diploma in Statistics Introduction to Regression 70

Reading SA Sections 1. 6, 8. 1, 8. 2, Diploma in Statistics Introduction to Regression 71