Introduction to Recursion Intro to Computer Science CS

Introduction to Recursion Intro to Computer Science CS 1510, Section 2 Dr. Sarah Diesburg

Sorting Complexity Three sorting algorithms Bubble Sort Insertion Sort Merge Sort All these algorithms are approximately n 2 Can we do better? 2

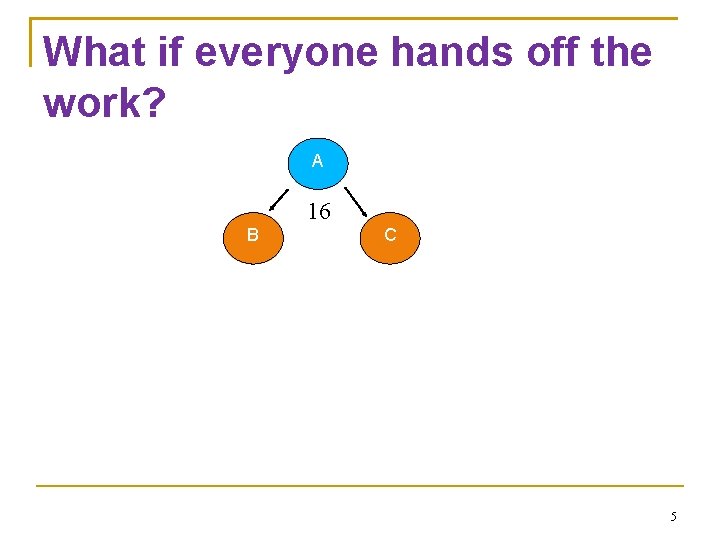
Sorting Programming Assignments Let’s say I have 16 programming assignments, and I need to sort them in alphabetical order I’m lazy, so I hand off half of the assignments to one student to sort, and the other half to another student to sort How many comparisons do I have to make to merge both sorted paper stacks? 3

Sorting Programming Assignments Let’s say I have 16 programming assignments, and I need to sort them in alphabetical order I’m lazy, so I hand off half of the assignments to one student to sort, and the other half to another student to sort How many comparisons do I have to make to merge both sorted paper stacks? Worst case: 1 pass, around n comparisons 4

What if everyone hands off the work? A 16 B C 5

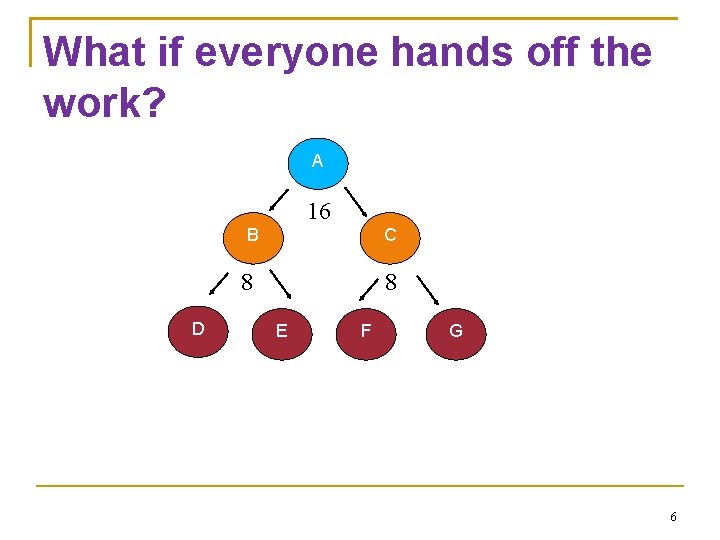
What if everyone hands off the work? A 16 B C 8 D 8 E F G 6

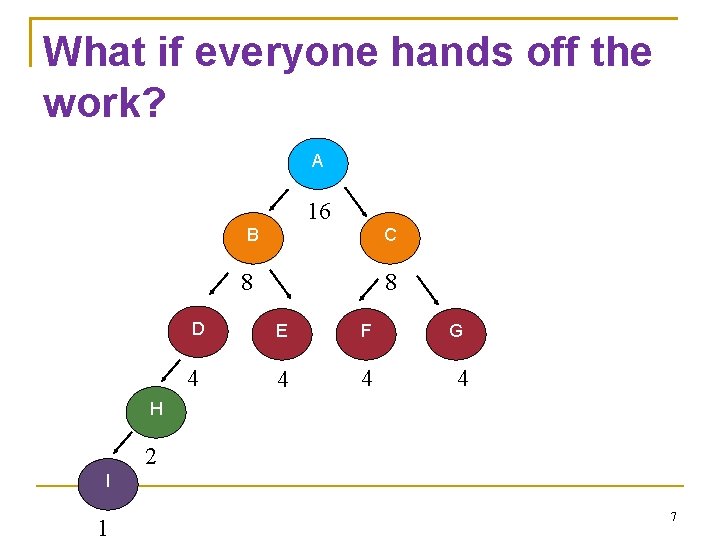
What if everyone hands off the work? A 16 B C 8 8 D E F 4 4 4 G 4 H 2 I 1 7

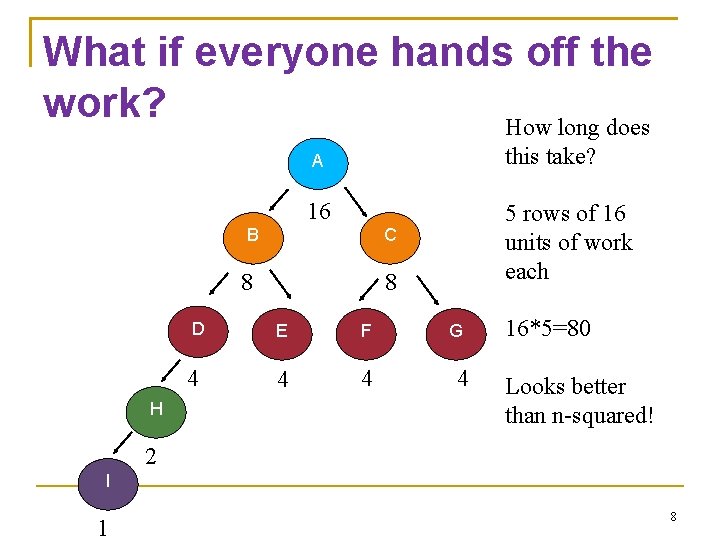
What if everyone hands off the work? How long does A this take? 16 5 rows of 16 units of work each B C 8 H 8 D E F 4 4 4 G 4 16*5=80 Looks better than n-squared! 2 I 1 8

How can we build a Merge Sort? We need to understand a new concept called recursion 9

A Function that Calls Itself The very basic meaning of a recursive function is a function that calls itself. However, when you first see it, it looks odd. Look at the recursive function that calculates factorial (code listing 16 -2).

Code Listing 16 -2 def factorial(n): """Recursive factorial. """ if n == 1: return 1 else: return n * factorial(n-1)

It Doesn’t Do Anything! This is a common complaint when one first sees a recursive function: “What exactly is it doing? It doesn’t seem to do anything!” Our goal is to understand what it means to write a recursive function from a programmer’s and computer’s point of view.

Defining a Recursive Function

1) Divide and Conquer Recursion is a natural outcome of a divide and conquer approach to problem solving. A recursive function defines how to break a problem down (divide) and how to reassemble (conquer) the sub-solutions into an overall solution.

2) Base Case Recursion is a process not unlike loop iteration. You must define how long (how many iterations) recursion will proceed until it stops. The base case defines this limit. Without the base case, recursion will continue infinitely (just like an infinite loop).

Simple Example Lao-Tzu: “A journey of 1000 miles begins with a single step. ” def journey (steps): the first step is easy (base case) the nth step is easy having completed the previous n-1 steps (divide and conquer)

Code Listing 16 -1 def take. Step(n): if n == 1: # base case return "Easy" else: this. Step = "step(" + str(n) + ")” # divide step, recurse previous. Steps = take. Step(n-1) # conquer step return this. Step + " + previous. Steps

Factorial You remember factorial? Factorial(4) = 4! = 4 * 3 * 2 * 1 The result of the last step, multiply by 1, is defined based on all the previous results that have been calculated.

Code Listing 16 -2 def factorial(n): """Recursive factorial. """ if n == 1: return 1 else: return n * factorial(n-1)

Trace the Calls 4! = 4 * 3! start first function invocation 3! = 3! * 2 start second function invocation 2! = 2 * 1! start third function invocation 1! = 1 fourth invocation, base case 2! = 2 * 1 = 2 third invocation finishes 3! = 3 * 2 = 6 second invocation finishes 4! = 4 * 6 = 24 first invocation finishes

Another: Fibonacci Depends on the Fibo results for the two previous values in the sequence. The base values are Fibo(0) == 1 and Fibo(1) == 1. fibo (x) = fibo(x-1) + fibo(x-2)

Code Listing 16 -3 def fibo(n): """Recursive Fibonacci sequence. """ if n == 0 or n == 1: # base case return 1 else: # divide and conquer return fibonacci(n-1) + fibonacci(n-2)

Trace fibo(4) = fibo(3) + fibo(2) fibo(3) = fibo(2) + fibo(1) fibo(2) = fibo(1) + fibo(0) = 2 # base case fibo(3) = 2 + fibo(1) = 3 # base case fibo(4) = 3 + 2 = 5