Introduction to Recursion Example 1 Factorial Example 2

Introduction to Recursion Ø Example 1: Factorial Ø Example 2: Reversing Strings Ø Example 3: Fibonacci Ø Infinite Recursion Ø Review Exercises 1

Introduction to Recursion Ø We saw earlier that a method can call another method leading to the creation of activation records on the runtime stack. Ø Recursion is one of the powerful techniques of solving problems. Ø A recursive method is a method that calls itself directly or indirectly Ø A well-defined recursive method has: Ø A base case that determines the stopping condition in the method Ø A recursive step which must always get “closer” to the base case from one invocation to another. Ø The code of a recursive method must be structured to handle both the base case and the recursive case. Ø Each call to the method sets up a new execution environment, with new parameters and local variables. 2

Example 1: The Factorial Function 1, if n = 0 factorial(n) = n*factorial(n-1), if n > 0 public class Factorial{ public static void main(String[] args){ long answer = factorial(5); System. out. println(answer); } public long factorial(int n) { if(n == 0) return 1 L; else return n*factorial(n-1); } 3

The Factorial: Sample Execution Trace factorial (6) = = = (6*factorial(5)) (6*(5*factorial(4))) (6*(5*(4*factorial(3)))) (6*(5*(4*(3*factorial(2))))) (6*(5*(4*(3*(2*factorial(1)))))) (6*(5*(4*(3*(2*1))))) (6*(5*(4*(3*2)))) (6*(5*(4*6))) (6*(5*24)) (6*120) 720 4

Example 2: Reversing Strings public void reverse. String(String str, int i) { if(i < str. length()){ reverse. String(str, i+1); System. out. print(str. char. At(i)); } } 5

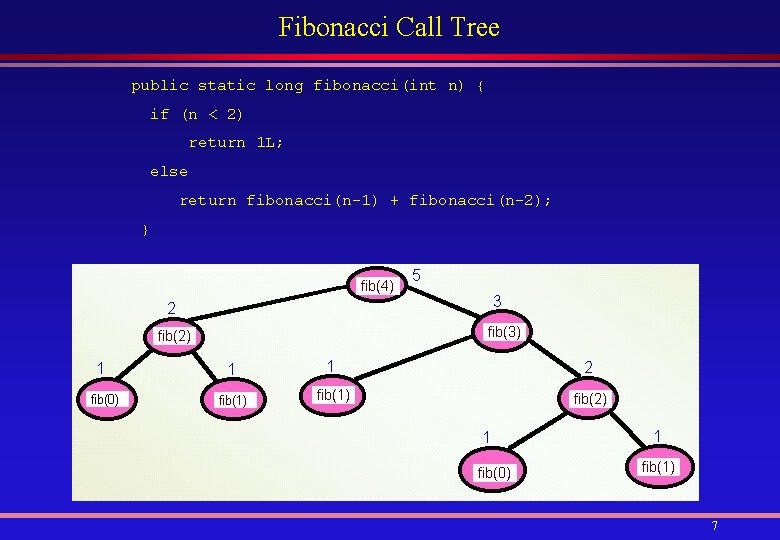
Example 3: The Fibonacci Function 1, fibonacci(n) = if n < 2 fibonacci(n-1) + fibonacci(n-2), public class Fibonacci{ public static void main(String[] args){ long answer = fibonacci(4); System. out. println(answer); } } if n >= 2 public static long fibonacci(int n) { if (n < 2) return 1 L; else return fibonacci(n-1) + fibonacci(n-2); } 6

Fibonacci Call Tree public static long fibonacci(int n) { if (n < 2) return 1 L; else return fibonacci(n-1) + fibonacci(n-2); } 7

Infinite Recursion Ø A recursive method must always call itself with a smaller argument Ø Infinite recursion results when: Ø The base case is omitted. Ø Recursive calls are not getting closer to the base case. Ø In theory, infinite recursive methods will execute “forever” Ø In practice, the system reports a stack overflow error. 8

Drill Questions 1. Write a recursive method public int sum. Up. To(int n) which adds up all integers from 1 to n. 2. Write a recursive method public int multiply(x, y) that multiplies two integers x and y using repeated additions and without using multiplication. 3. Write a recursive method public int decimal. To. Binary(int n) that takes and integer parameter and prints its binary equivalent. 4. Write a recursive method public boolean is. Palindrome(String str) that returns true if str is a palindrome and returns false otherwise. Note: a palindrome is a string that has the same characters when read from left to right or from right to left (Examples: eye, radar, madam, dad, mom, 202). 9