Introduction to RealTime Systems Lecture 2 By Mohammad

Introduction to Real-Time Systems Lecture 2 By: Mohammad hajibegloo@gmail. com 1

Real-time Scheduling • Static scheduling • Scheduler has complete knowledge of task set and its constraints (ci, Ti) • Dynamic scheduling • Scheduler has complete knowledge of the current active set of tasks, but new arrivals may occur in the future 2

Schedulability Test to determine whether a feasible schedule exists • Sufficient Test • If test is passed, then tasks are definitely schedulable • If test is not passed, tasks may be schedulable, but not necessarily • Necessary Test • If test is passed, tasks may be schedulable, but not necessarily • If test is not passed, tasks are definitely not schedulable • Exact Test (= Necessary + Sufficient) • The task set is schedulable if and only if it passes the test. 3

Scheduling Approaches • Off-line scheduling / analysis (static analysis + static scheduling) • • All tasks, times and priorities given a priori (before system startup) Time-driven; schedule computed and hardcoded (before system startup) E. g. , Cyclic Executives Inflexible • Fixed priority scheduling (static analysis + dynamic scheduling) • All tasks, times and priorities given a priori (before system startup) • Priority-driven, dynamic scheduling • The schedule is constructed by the OS scheduler at run time • For hard real time systems • E. g. , RM (Rate Monotonic) • Dynamic priority scheduling • • Tasks times may or may not be known Assigns priorities based on the current state of the system For hard / best effort systems E. g. , Earliest Deadline, First (EDF) 4

Periodic Task Scheduling 5

Periodic Task Scheduling Notation Ti denotes the period of task i Ci denotes the Computation time for one instance of task i 6

Periodic Task Scheduling Assumptions 7

Rate Monotonic Scheduling 8

Paper Scheduling Algorithms for Multiprogramming in a Hard Real-Time Environment C. L. Liu and James W. Layland © 1973 9

Rate Monotonic Scheduling • Rate Monotonic scheduling algorithm: üAssigns priorities to tasks according to their request rates. • Tasks with higher request rates will have higher priorities • Periods are constant (RM is a fixed-priority assignment) ü Priorities are assigned to tasks before execution and do not change over time = static scheduling üRM is intrinsically preemptive • The currently executing task is preempted by a newly arrived task with shorter period. 10

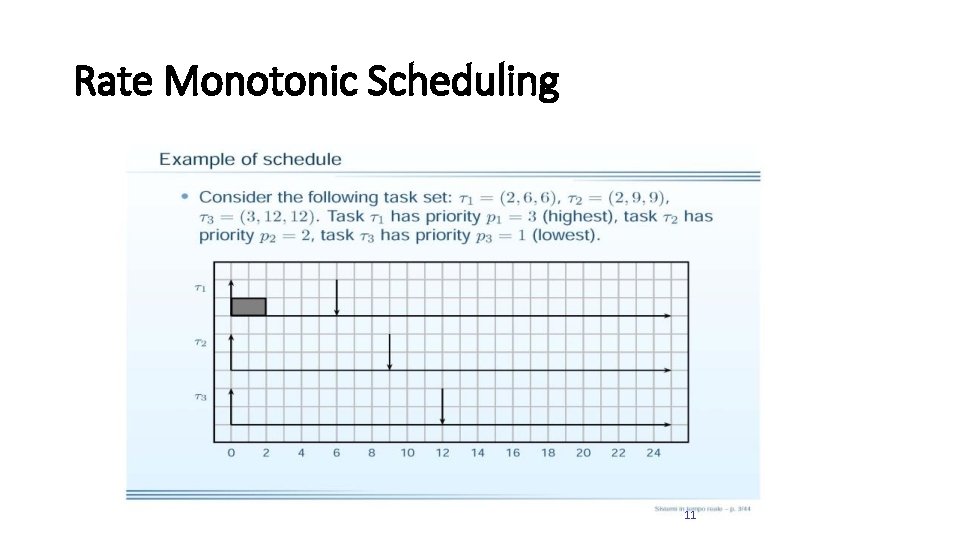
Rate Monotonic Scheduling 11

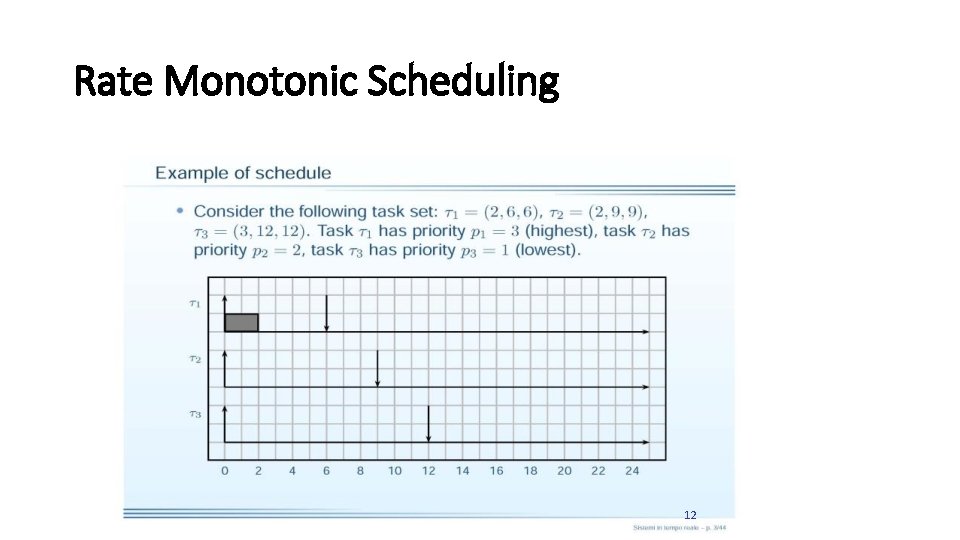
Rate Monotonic Scheduling 12

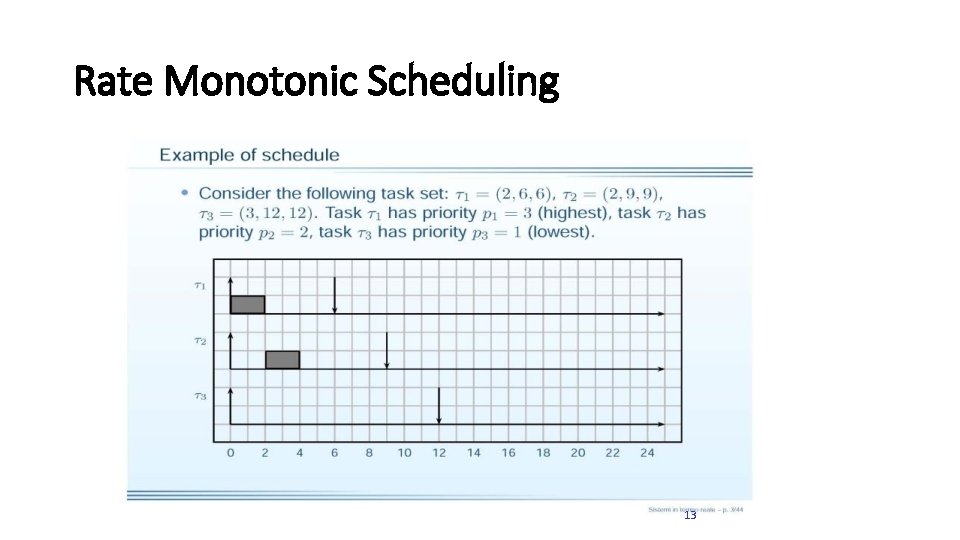
Rate Monotonic Scheduling 13

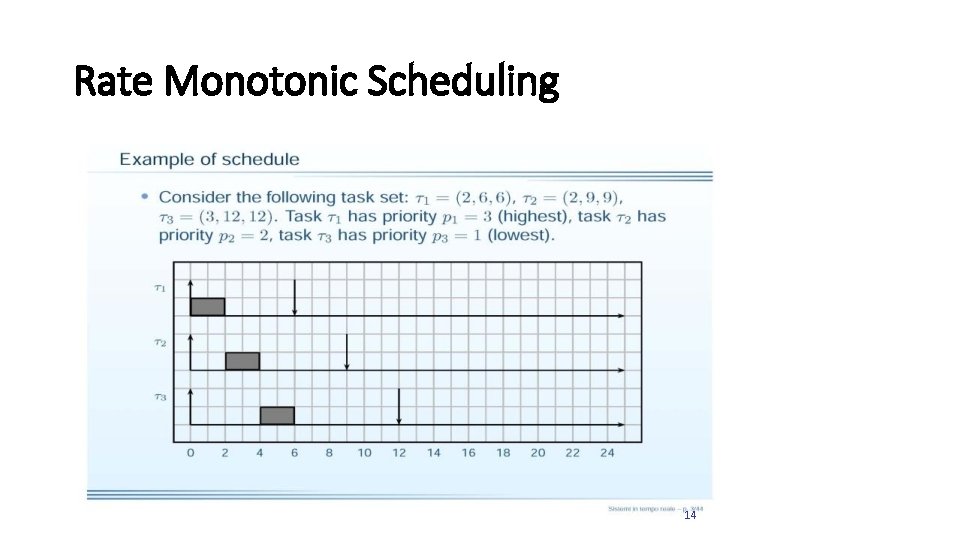
Rate Monotonic Scheduling 14

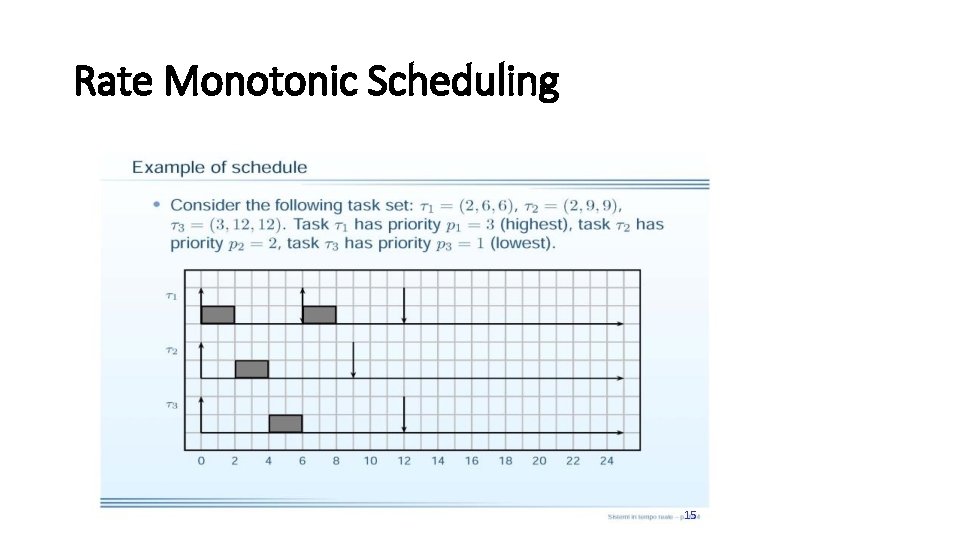
Rate Monotonic Scheduling 15

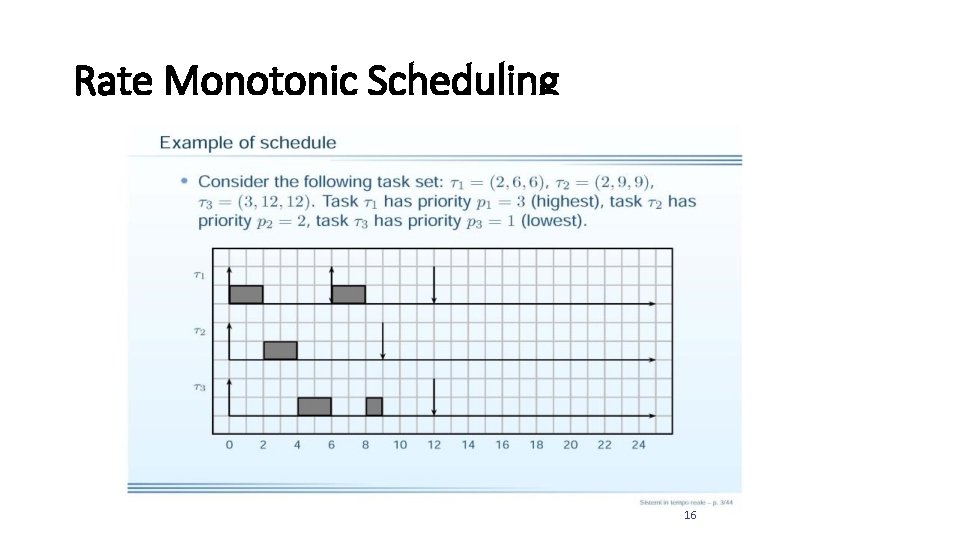
Rate Monotonic Scheduling 16

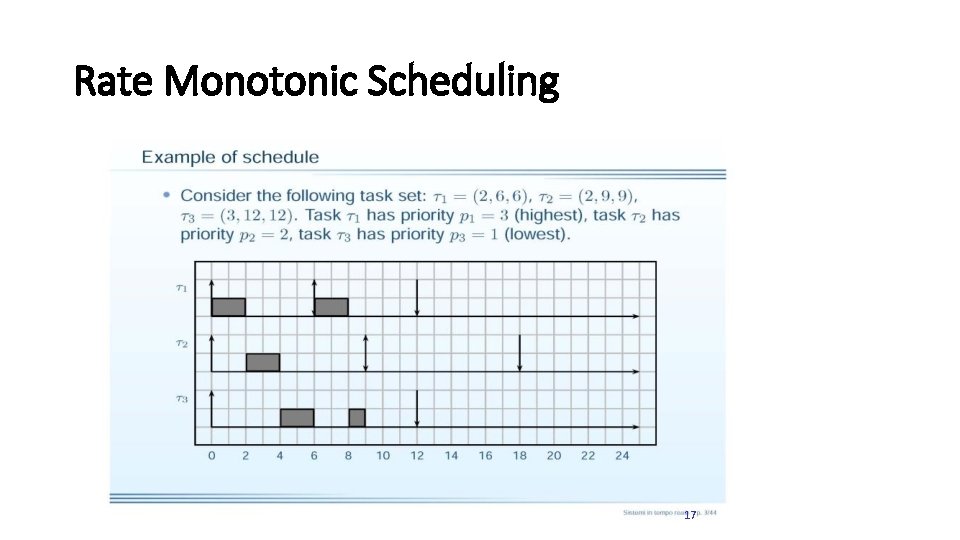
Rate Monotonic Scheduling 17

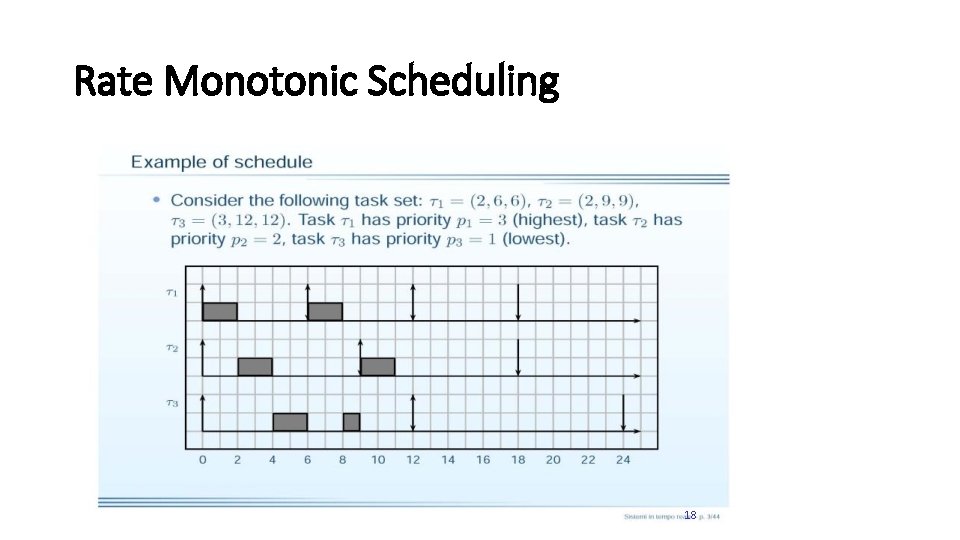
Rate Monotonic Scheduling 18

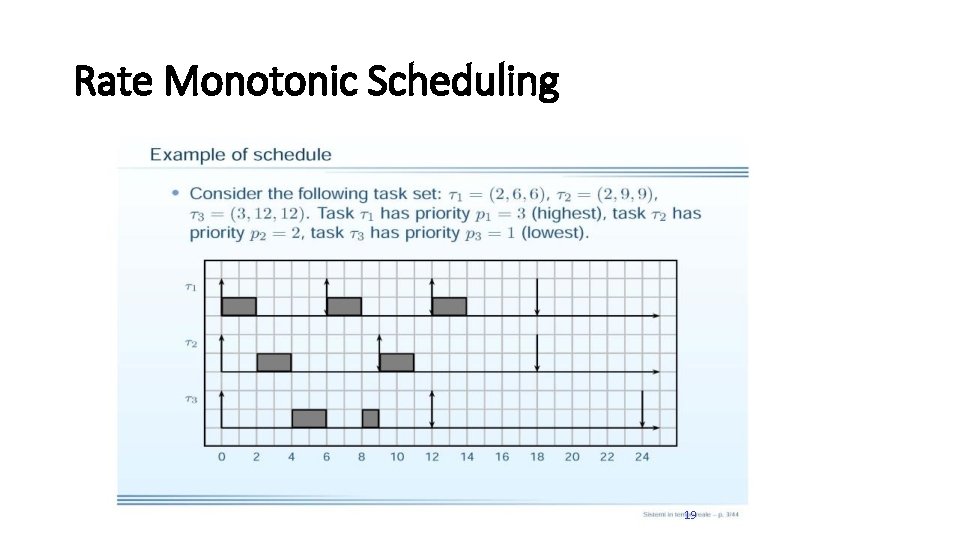
Rate Monotonic Scheduling 19

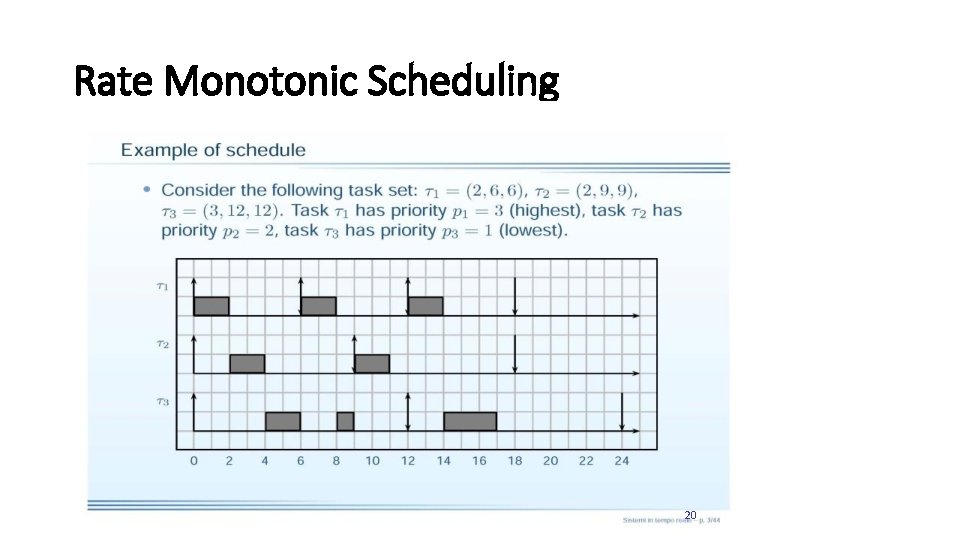
Rate Monotonic Scheduling 20

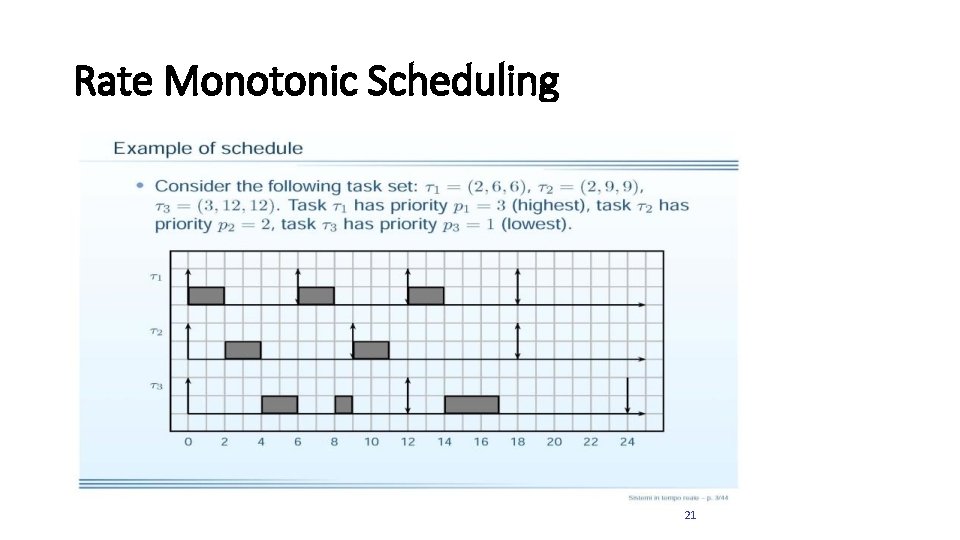
Rate Monotonic Scheduling 21

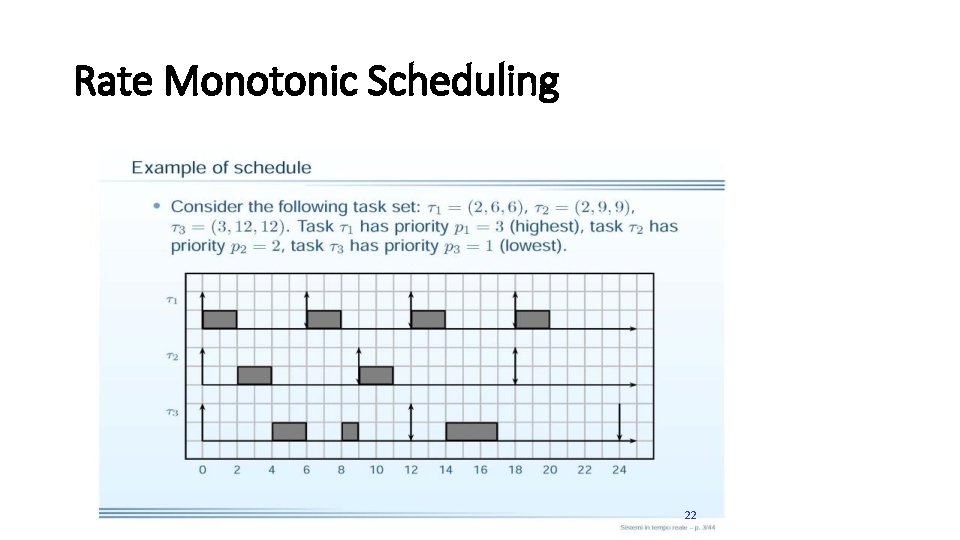
Rate Monotonic Scheduling 22

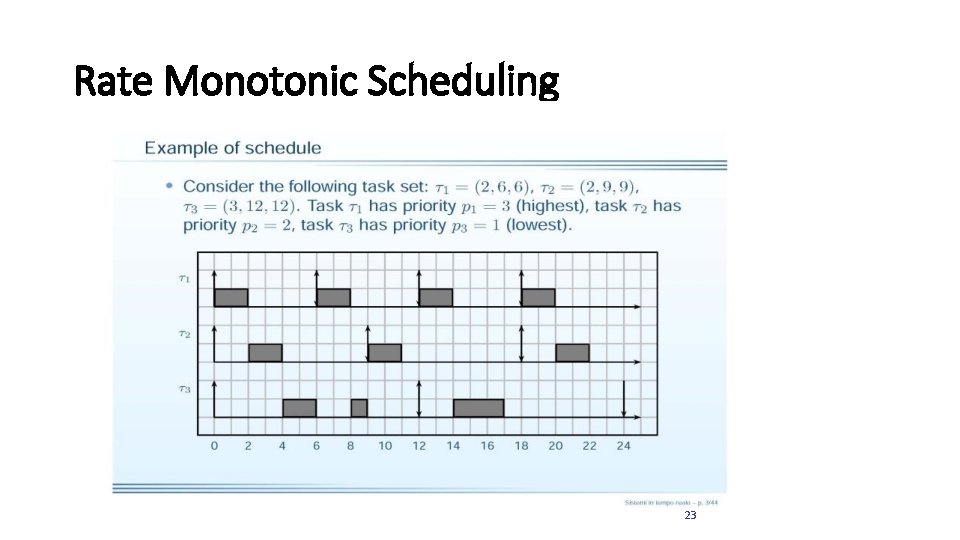
Rate Monotonic Scheduling 23

Definitions • The deadline of a request for a task : • Time of the next request for the same task. • Overflow: • occurs at time t if t is the deadline of an unfulfilled request. • A scheduling algorithm is feasible if the tasks are scheduled so that no overflow ever occurs. • The response time of a request: • the time span between the request and the end of the response to that request. 24

Definitions • A critical instant for a task: • an instant at which a request for that task will have the largest response time. • A critical time zone for a task: • The time interval between a critical instant and the end of the response to the corresponding request of the task. 25

A fixed priority scheduling algorithm THEOREM 1: A critical instant for any task occurs whenever the task is requested simultaneously with requests for all higher priority tasks. 26

Proof of Theorem 1 27

A fixed priority scheduling algorithm • consider a set of two tasks τ1 and τ2 with T 1 = 2, T 2 = 5, and C 1=1, C 2 = 1. • If τ1 is the higher priority then the maximum value for C 2 is equal 2. • If τ2 is the higher priority then the maximum value for C 2 and C 1 is equal 1. 28

A fixed priority scheduling algorithm • consider a set of two tasks τ1 and τ2 T 1 < T 2 • If τ1 is the higher priority then it is necessary that: (1) • If τ2 is the higher priority then: (2) 2 implies 1. 29

A fixed priority scheduling algorithm • If T 1 < T 2 and the task schedule is feasible with τ2 at higher priority than τ1 • It is also feasible with τ1 at higher priority than τ2 , but the opposite is not true. • we should assign higher priority to τ1 and lower priority to τ2. (Rate monotonic priority assignment) 30

A fixed priority scheduling algorithm THEOREM 2. If a feasible priority assignment exists for some task set, the rate monotonic priority assignment is feasible for that task set. RM is optimal among all fixed Priority assignment schedules. Why? How can you how show that it must be optimal? 31

A fixed priority scheduling algorithm Proof of THEOREM 2: 32

Processor Utilization Factor - U • Utilization factor: • the fraction of processor time spent in the execution of the task set < 1 if set is scheduable • Fully utilize: • the processor if the priority assignment is feasible for the set and if an increase in the run-time of any of the tasks in the set will make the priority assignment infeasible. 33

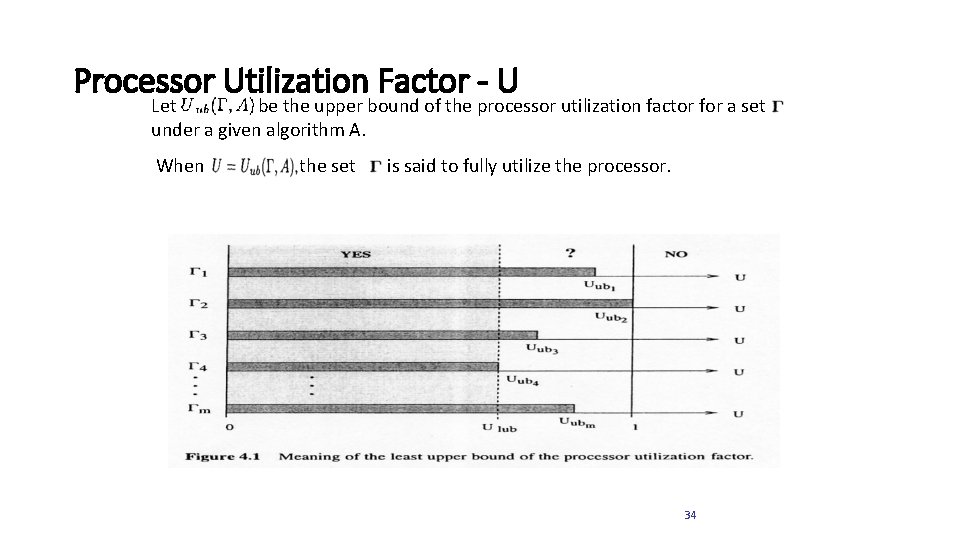
Processor Utilization Factor - U Let be the upper bound of the processor utilization factor for a set under a given algorithm A. When the set is said to fully utilize the processor. 34

Processor Utilization Factor - U • Least upper bound of the utilization factor: • The minimum of the utilization factors over all sets of tasks that fully utilize the processor • utilization above this bound can only be achieved if the Ti , of the tasks are suitably related. 1 35

Rate Monotonic – Calc of ULUB for Two Tasks THEOREM 3. For a set of two tasks with fixed priority assignment, the least upper bound to the processor utilization factor is 36

Rate Monotonic – Calc of ULUB for Two Tasks Let , the number of 37

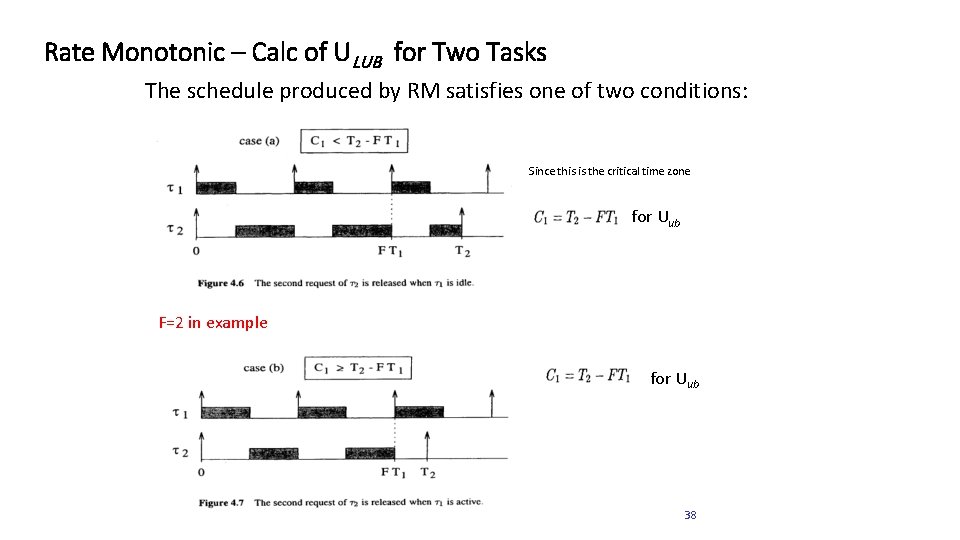
Rate Monotonic – Calc of ULUB for Two Tasks The schedule produced by RM satisfies one of two conditions: Since this is the critical time zone for Uub F=2 in example for Uub 38

Rate Monotonic – Calc of ULUB for Two Tasks Case 1: Uub is monotonically descries in C 1 39

Rate Monotonic – Calc of ULUB for Two Tasks Case 2: Uub is monotonically increase in C 1 40

41

42

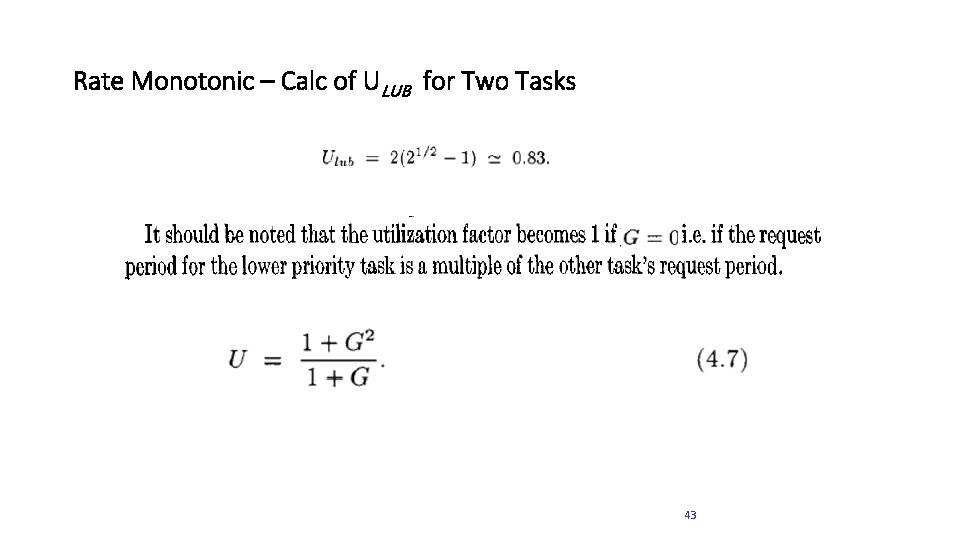
Rate Monotonic – Calc of ULUB for Two Tasks 43

Rate Monotonic – Calc of ULUB for Two Tasks 44

Rate Monotonic – Calc of ULUB for n Tasks THEOREM 4. For a set of m tasks with fixed priority order, and the restriction that the ratio between any two request periods is less than 2, the least upper bound to the processor utilization factor is 45

46

47

48

Rate Monotonic Scheduling 49