Introduction to Quantum Information Processing CS 467 CS

Introduction to Quantum Information Processing CS 467 / CS 667 Phys 467 / Phys 767 C&O 481 / C&O 681 Lecture 6 (2005) Richard Cleve DC 3524 cleve@cs. uwaterloo. ca Course web site at: http: //www. cs. uwaterloo. ca/~cleve 1

Contents • Phase estimation problem • Algorithm for the phase estimation problem • Order-finding via phase estimation 2

• Phase estimation problem • Algorithm for the phase estimation problem • Order-finding via phase estimation 3

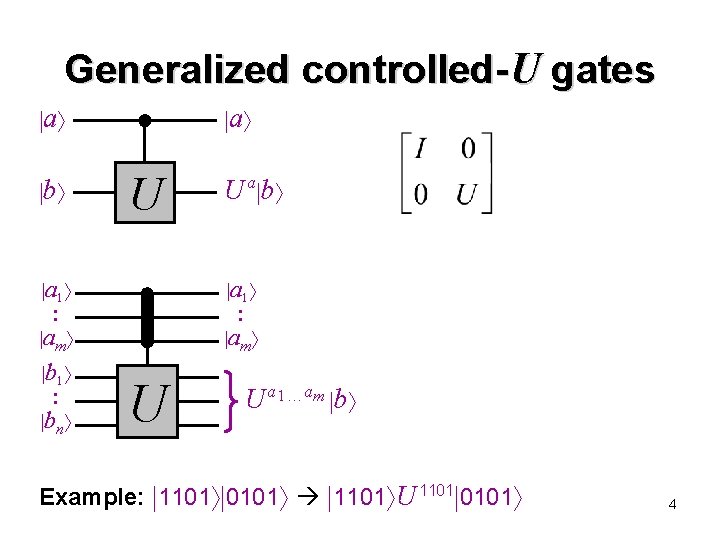
Generalized controlled-U gates a b a U a 1 : am b 1 : bn U a b a 1 : am U U a 1 am b Example: 1101 0101 1101 U 1101 0101 4

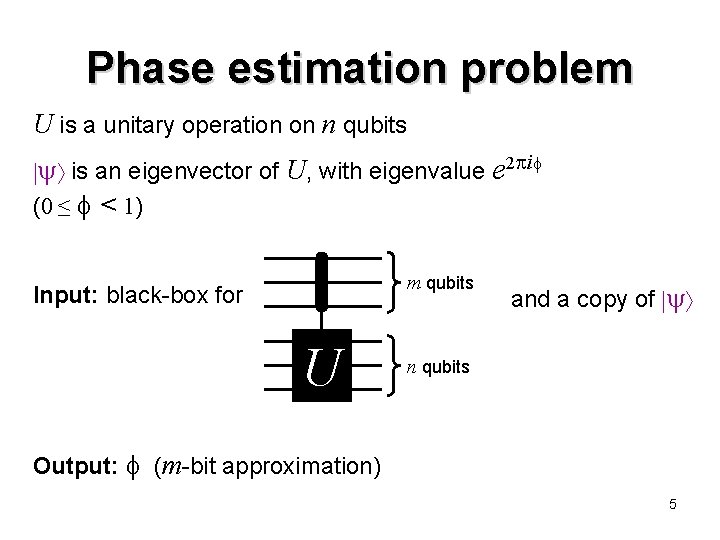
Phase estimation problem U is a unitary operation on n qubits is an eigenvector of U, with eigenvalue e 2 i (0 ≤ < 1) m qubits Input: black-box for U and a copy of n qubits Output: (m-bit approximation) 5

• Phase estimation problem • Algorithm for the phase estimation problem • Order-finding via phase estimation 6

Algorithm for phase estimation (I) Starts off as: 0 0 0 H H H U 00 … 0 ( 0 + 1 ) … ( 0 + 1 ) a b a U a b = ( 000 + 001 + 010 + 011 + … + 111 ) = ( 0 + 1 + 2 + 3 + … + 2 m 1 ) ( 0 + e 2 i 1 + (e 2 i )2 2 + (e 2 i )3 3 + … + (e 2 i )2 2 m 1 ) m� 1 7

Quantum Fourier transform where = e 2 i/N (for n qubits, N = 2 n) 8

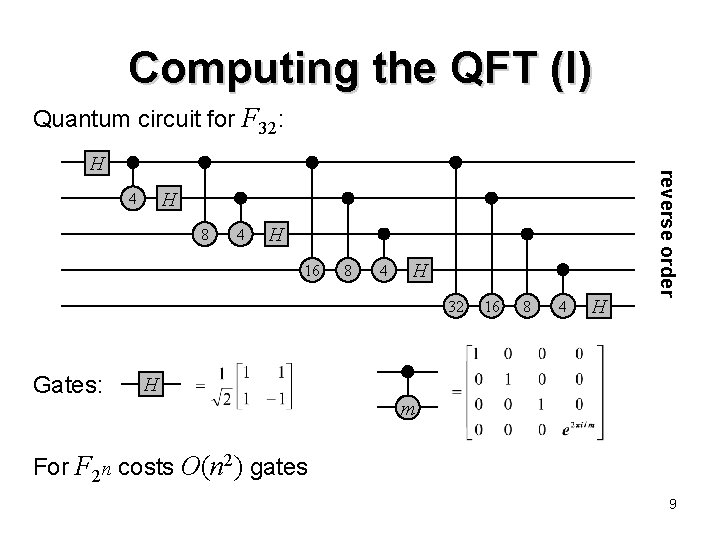
Computing the QFT (I) Quantum circuit for F 32: H 4 8 4 H 16 8 4 H 32 Gates: 16 8 4 H reverse order H H m For F 2 n costs O(n 2) gates 9

Computing the QFT (II) One way on seeing why this circuit works is to first note that F 2 n a 1 a 2…an = ( 0 + e 2 i (0. an) 1 )…( 0 + e 2 i (0. a 2…an) 1 ) ( 0 + e 2 i (0. a 1 a 2…an) 1 ) It can then be checked that the circuit produces these states (with qubits in reverse order) for all computational basis states a 1 a 2…an Exercise: (a) prove the above equation from the definition of the QFT; (b) confirm that the circuit produces these states 10

Algorithm for phase estimation (II) Note: this is exactly the state generated by our preliminary algorithm for phase estimation when = 0. a 1 a 2…am Therefore, if = 0. a 1 a 2…am then applying F† to this state yields a 1 a 2…am (from which can be deduced exactly) What if is not of this nice form? Example: = ⅓ = 0. 01010101… 11

• Phase estimation problem • Algorithm for the phase estimation problem • Order-finding via phase estimation 12

Order-finding algorithm (I) Let M be an m-bit integer Def: ZM* = {x {1, 2, …, M 1} : gcd(x, M ) = 1} ZM* is a group under multiplication modulo M Example: Z 21* = {1, 2, 4, 5, 8, 10, 11, 13, 16, 17, 19, 20} For a ZM*, consider all powers of a : a 0, a 1, a 2, a 3, … Ex: For a = 10, the sequence is: 1, 10, 16, 13, 4, 19, 1, 10, 16, … Def: ord. M (a) is the minimum r > 0 such that ar = 1 (mod M ) Ex: ord 21 (10) = 6 Order-finding problem: given a and M, find ord. M (a) 13

Order-finding algorithm (II) Define: U (an operation on m qubits) as: U y = a y mod M Define: Then 14

Order-finding algorithm (III) U 2 n qubits corresponds to the mapping: x y x ax y mod M n qubits Moreover, this mapping can be implemented with roughly O(n 2) gates The phase estimation algorithm yields a 2 n-bit estimate of 1/r From this, a good estimate of r can be calculated … Problem: how do we construct state 1 to begin with? 15

16