Introduction to Quantum Information Processing CS 467 CS

Introduction to Quantum Information Processing CS 467 / CS 667 Phys 667 / Phys 767 C&O 481 / C&O 681 Lecture 1 (2008) Richard Cleve DC 2117 cleve@cs. uwaterloo. ca 1

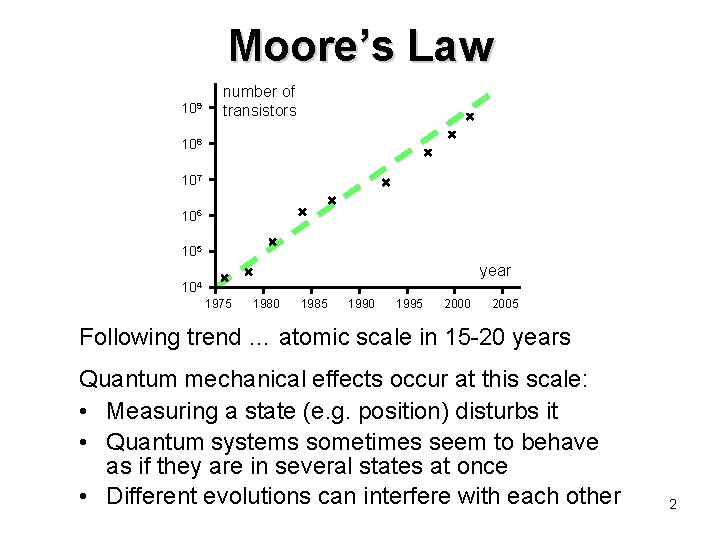
Moore’s Law 109 number of transistors 108 107 106 105 year 104 1975 1980 1985 1990 1995 2000 2005 Following trend … atomic scale in 15 -20 years Quantum mechanical effects occur at this scale: • Measuring a state (e. g. position) disturbs it • Quantum systems sometimes seem to behave as if they are in several states at once • Different evolutions can interfere with each other 2

Quantum mechanical effects Additional nuisances to overcome? or New types of behavior to make use of? [Shor, 1994]: polynomial-time algorithm for factoring integers on a quantum computer This could be used to break most of the existing public-key cryptosystems on the internet, such as RSA 3

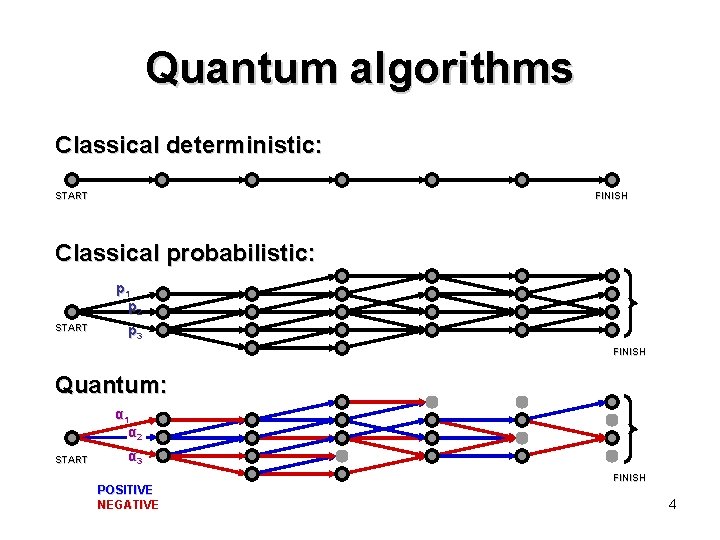
Quantum algorithms Classical deterministic: START FINISH Classical probabilistic: p 1 p 2 START p 3 FINISH Quantum: α 1 α 2 START α 3 POSITIVE NEGATIVE FINISH 4

Also with quantum information: • Faster algorithms for combinatorial search [Grover ’ 96] • Unbreakable codes with short keys [Bennett, Brassard ’ 84] • Communication savings in distributed systems [C, Buhrman ’ 97] • More efficient “proof systems” [Watrous ’ 99] … and an extensive quantum information theory arises, which generalizes classical information theory For example: a theory of quantum error-correcting codes quantum information theory classical information theory 5

This course covers the basics of quantum information processing Topics include: • Quantum algorithms and complexity theory • Quantum information theory • Quantum error-correcting codes • Physical implementations* • Quantum cryptography • Quantum nonlocality and communication complexity 6

General course information Background: • classical algorithms and complexity • linear algebra • probability theory Evaluation: • 5 assignments (12% each) • project presentation (40%) Recommended texts: An Introduction to Quantum Computation, P. Kaye, R. Laflamme, M. Mosca (Oxford University Press, 2007). Primary reference. Quantum Computation and Quantum Information, Michael A. Nielsen and Isaac L. Chuang (Cambridge University Press, 2000). Secondary reference. 7

Basic framework of quantum information 8

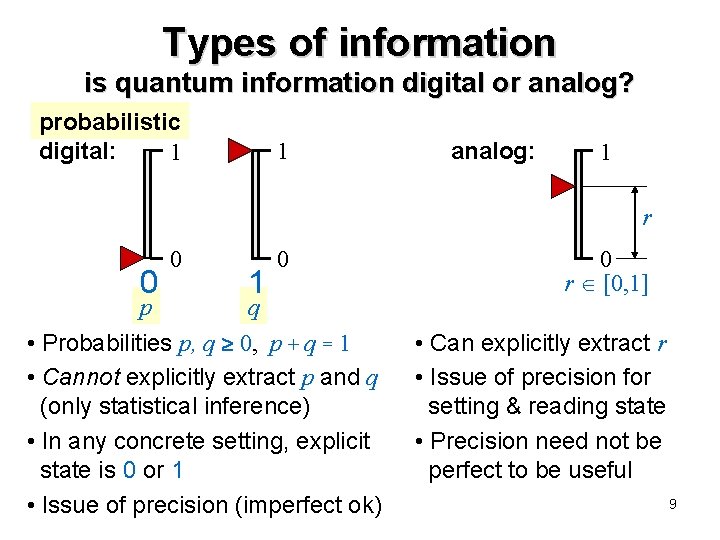
Types of information is quantum information digital or analog? probabilistic digital: 1 1 analog: 1 r 0 0 1 0 p q • Probabilities p, q 0, p + q = 1 • Cannot explicitly extract p and q (only statistical inference) • In any concrete setting, explicit state is 0 or 1 • Issue of precision (imperfect ok) 0 r [0, 1] • Can explicitly extract r • Issue of precision for setting & reading state • Precision need not be perfect to be useful 9

Quantum (digital) information 0 1 1 0 0 1 • Amplitudes , C, | |2 + | |2 = 1 • Explicit state is • Cannot explicitly extract and (only statistical inference) • Issue of precision (imperfect ok) 10

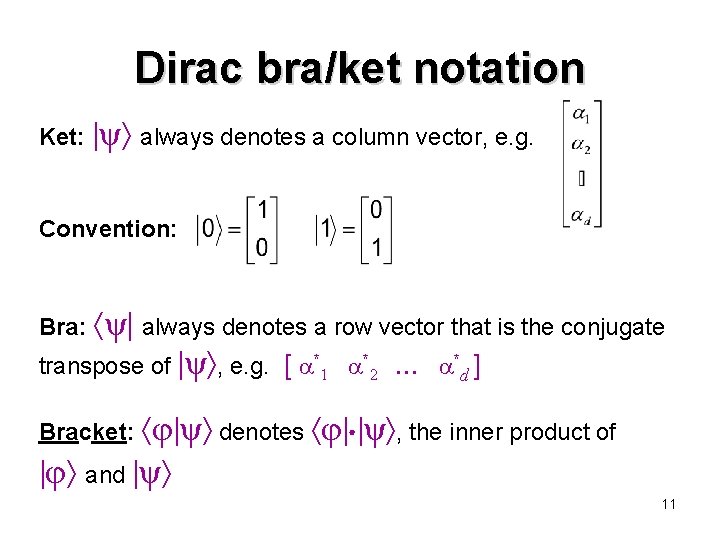
Dirac bra/ket notation Ket: ψ always denotes a column vector, e. g. Convention: Bra: ψ always denotes a row vector that is the conjugate transpose of ψ , e. g. [ *1 *2 *d ] Bracket: φ ψ denotes φ ψ , the inner product of φ and ψ 11

Basic operations on qubits (I) (0) Initialize qubit to |0 or to |1 † (1) Apply a unitary operation U (U U = I ) Examples: Rotation: NOT (bit flip): Hadamard: Phase flip: 12

Basic operations on qubits (II) (3) Apply a “standard” measurement: 0 + 1 ψ′ 1 ψ | |2 0 | |2 … and the quantum state collapses ( ) There exist other quantum operations, but they can all be “simulated” by the aforementioned types Example: measurement with respect to a different orthonormal basis { ψ , ψ′ } 13

Distinguishing between two states Let be in state or Question 1: can we distinguish between the two cases? Distinguishing procedure: 1. apply H 2. measure This works because H + = 0 and H − = 1 Question 2: can we distinguish between 0 and + ? Since they’re not orthogonal, they cannot be perfectly distinguished … 14

n-qubit systems Probabilistic states: Quantum states: Dirac notation: |000 , |001 , |010 , …, |111 are basis vectors, so 15

Operations on n-qubit states Unitary operations: (U†U = I ) Measurements: ? … and the quantum state collapses 16

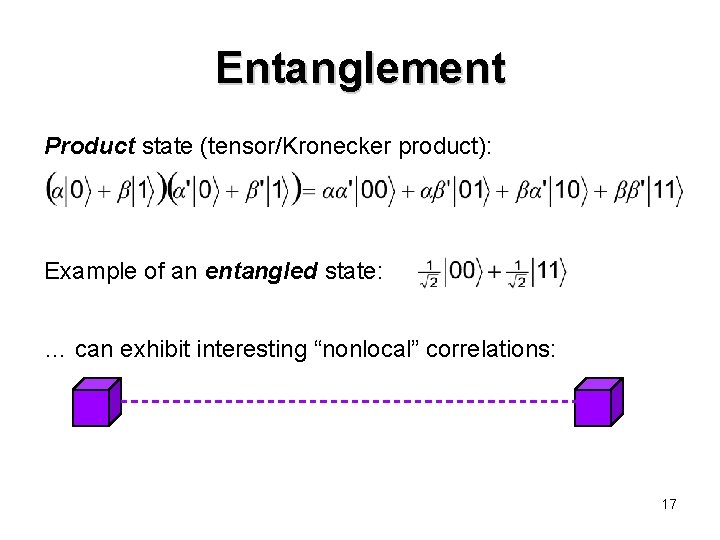
Entanglement Product state (tensor/Kronecker product): Example of an entangled state: … can exhibit interesting “nonlocal” correlations: 17

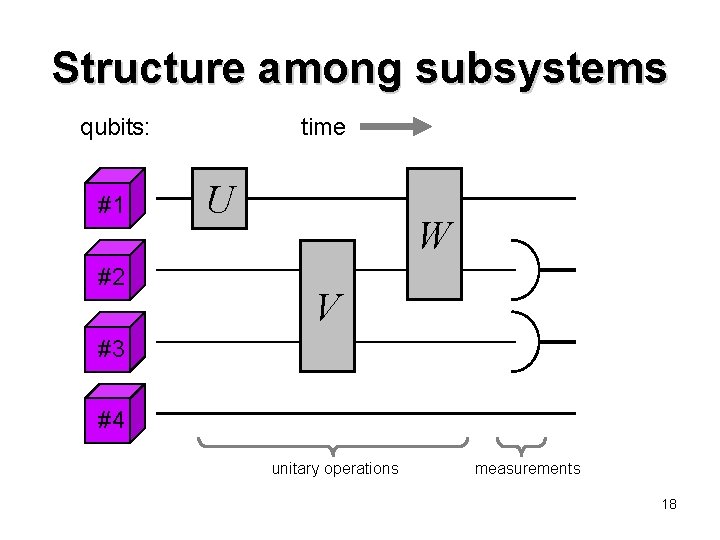
Structure among subsystems qubits: #1 #2 time U W V #3 #4 unitary operations measurements 18

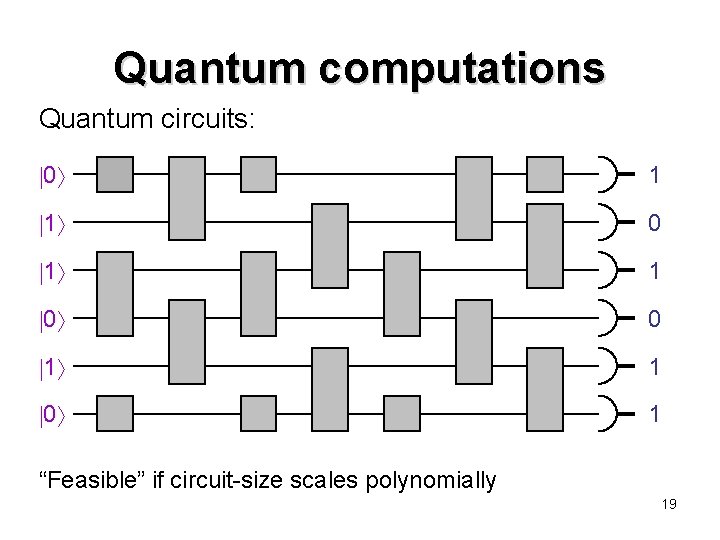
Quantum computations Quantum circuits: 0 1 1 0 1 “Feasible” if circuit-size scales polynomially 19

Example of a one-qubit gate applied to a two-qubit system (do nothing) U The resulting 4 x 4 matrix is Maps basis states as: 0 0 0 U 0 0 1 0 U 1 1 0 1 U 0 1 1 1 U 1 20

Controlled-U gates U Resulting 4 x 4 matrix is controlled-U = Maps basis states as: 0 0 0 1 1 0 1 U 0 1 1 1 U 1 21

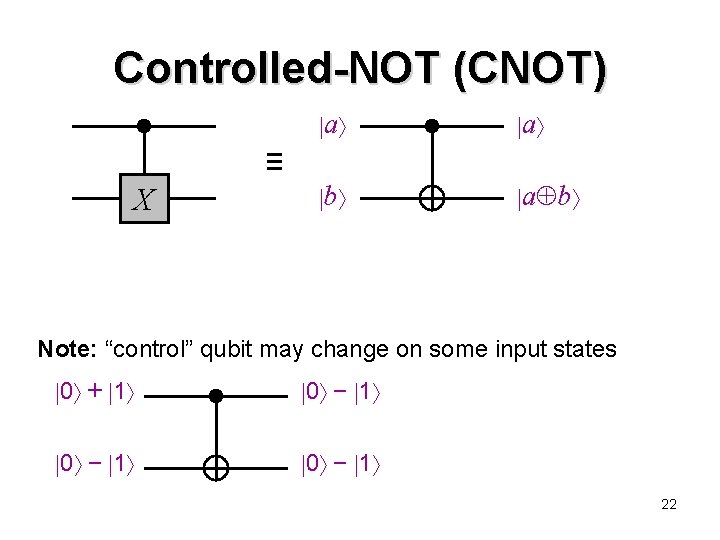
Controlled-NOT (CNOT) a a b a b ≡ X Note: “control” qubit may change on some input states 0 + 1 0 − 1 22

Introduction to Quantum Information Processing CS 467 / CS 667 Phys 667 / Phys 767 C&O 481 / C&O 681 Lecture 2 (2008) Richard Cleve DC 2117 cleve@cs. uwaterloo. ca 23

Superdense coding 24

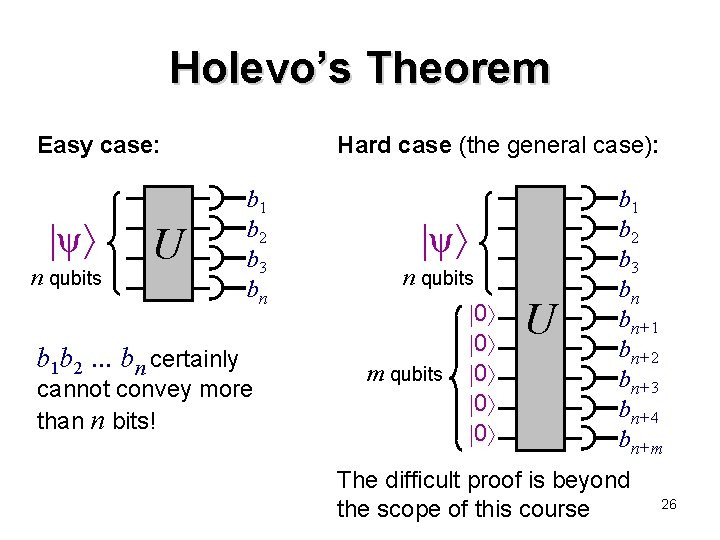
How much classical information in n qubits? 2 n 1 complex numbers apparently needed to describe an arbitrary n-qubit pure quantum state: 000 + 001 + 010 + + 111 Does this mean that an exponential amount of classical information is somehow stored in n qubits? Not in an operational sense. . . For example, Holevo’s Theorem (from 1973) implies: one cannot convey more than n classical bits of information in n qubits 25

Holevo’s Theorem Easy case: ψ n qubits U b 1 b 2 . . . bn certainly Hard case (the general case): b 1 b 2 b 3 bn cannot convey more than n bits! ψ n qubits m qubits 0 0 0 U b 1 b 2 b 3 bn bn+1 bn+2 bn+3 bn+4 bn+m The difficult proof is beyond the scope of this course 26

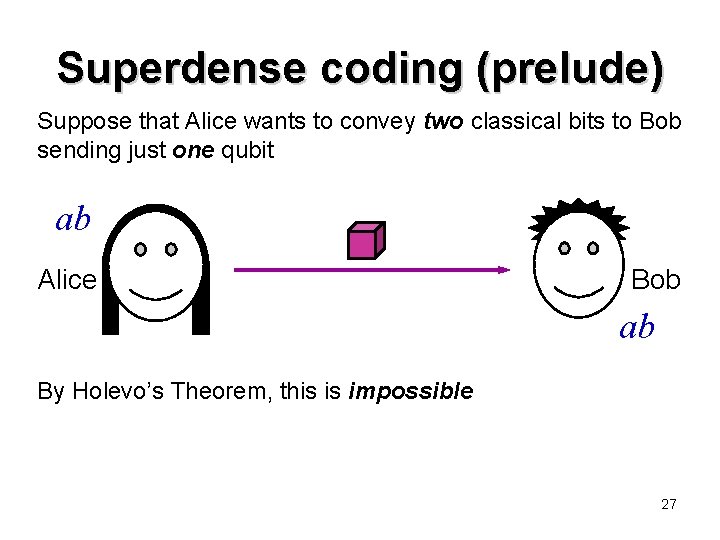
Superdense coding (prelude) Suppose that Alice wants to convey two classical bits to Bob sending just one qubit ab Alice Bob ab By Holevo’s Theorem, this is impossible 27

Superdense coding In superdense coding, Bob is allowed to send a qubit to Alice first ab Alice Bob ab How can this help? 28

How superdense coding works 1. Bob creates the state 00 + 11 and sends the first qubit to Alice 2. Alice: if a = 1 then apply X to qubit if b = 1 then apply Z to qubit send the qubit back to Bob ab state 00 + 11 00 − 11 10 01 + 10 11 01 − 10 Bell basis 3. Bob measures the two qubits in the Bell basis 29

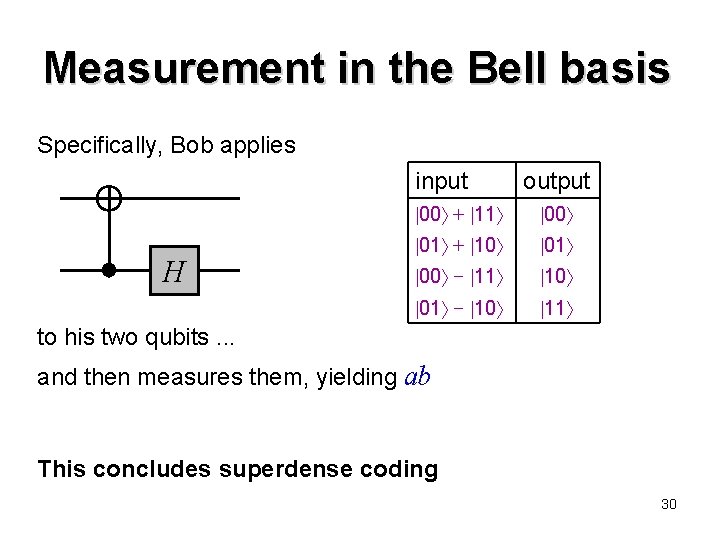
Measurement in the Bell basis Specifically, Bob applies input H output 00 + 11 00 01 + 10 01 00 − 11 10 01 − 10 11 to his two qubits. . . and then measures them, yielding ab This concludes superdense coding 30

Introduction to Quantum Information Processing CS 467 / CS 667 Phys 667 / Phys 767 C&O 481 / C&O 681 Lecture 3 (2008) Richard Cleve DC 2117 cleve@cs. uwaterloo. ca 31

Teleportation 32

Recap • n-qubit quantum state: 2 n-dimensional unit vector † • Unitary op: operation U such that U U = I † (where U denotes the conjugate transpose of U ) 2 n 2 n linear U 0000 = the 1 st column of U U 0001 = the 2 nd column of U the columns of U : are orthonormal : : : U 1111 = the (2 n)th column of U 33

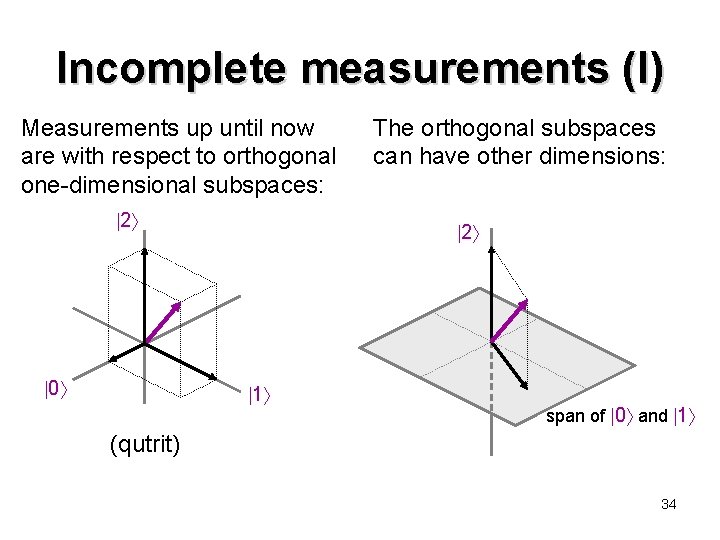
Incomplete measurements (I) Measurements up until now are with respect to orthogonal one-dimensional subspaces: 2 0 The orthogonal subspaces can have other dimensions: 2 1 span of 0 and 1 (qutrit) 34

Incomplete measurements (II) Such a measurement on 0 0 + 1 1 + 2 2 (renormalized) results in 0 0 + 1 1 with prob 0 2 + 1 2 2 with prob 2 2 35

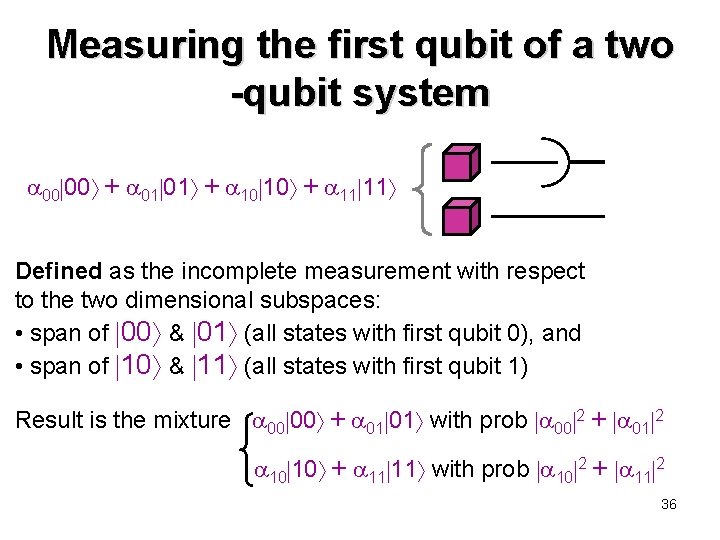
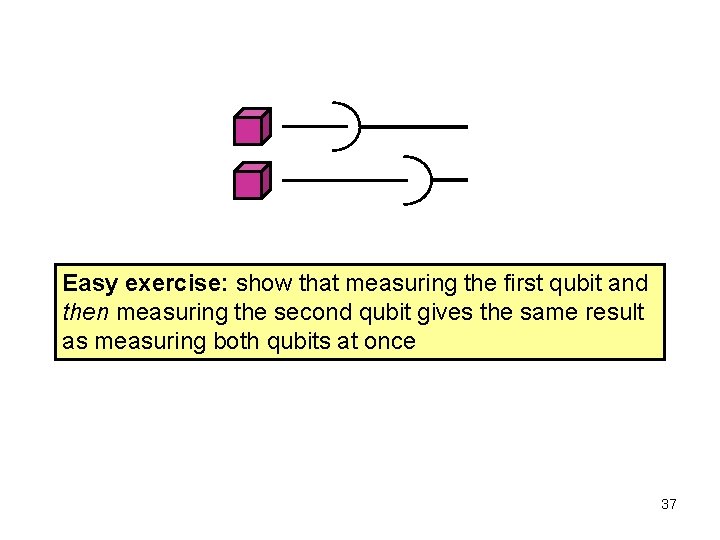
Measuring the first qubit of a two -qubit system 00 00 + 01 01 + 10 10 + 11 11 Defined as the incomplete measurement with respect to the two dimensional subspaces: • span of 00 & 01 (all states with first qubit 0), and • span of 10 & 11 (all states with first qubit 1) Result is the mixture 00 00 + 01 01 with prob 00 2 + 01 2 10 10 + 11 11 with prob 10 2 + 11 2 36

Easy exercise: show that measuring the first qubit and then measuring the second qubit gives the same result as measuring both qubits at once 37

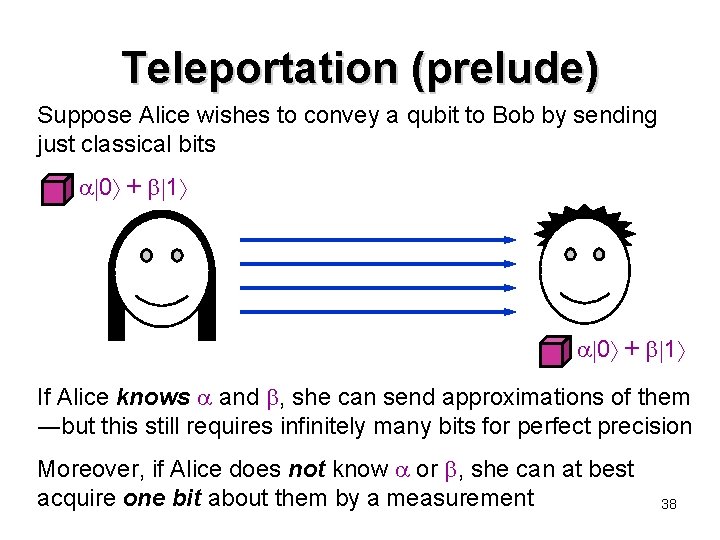
Teleportation (prelude) Suppose Alice wishes to convey a qubit to Bob by sending just classical bits 0 + 1 If Alice knows and , she can send approximations of them ―but this still requires infinitely many bits for perfect precision Moreover, if Alice does not know or , she can at best acquire one bit about them by a measurement 38

Teleportation scenario In teleportation, Alice and Bob also start with a Bell state 0 + 1 (1/ 2)( 00 + 11 ) and Alice can send two classical bits to Bob Note that the initial state of the three qubit system is: (1/ 2)( 0 + 1 )( 00 + 11 ) = (1/ 2)( 000 + 011 + 100 + 111 ) 39

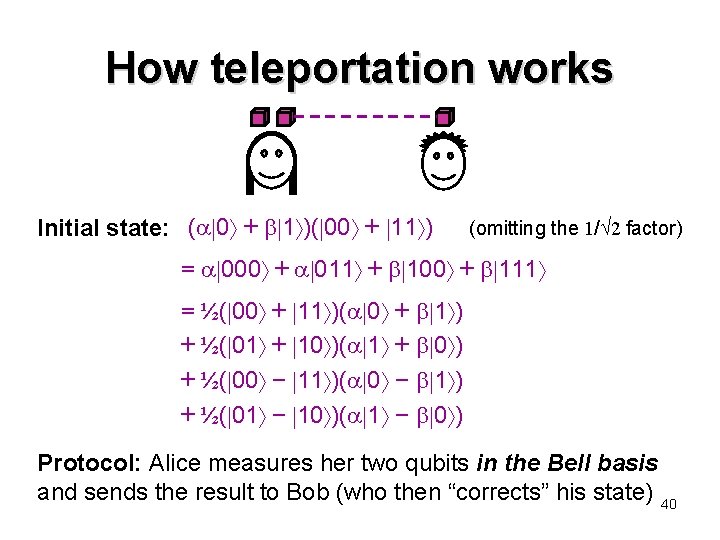
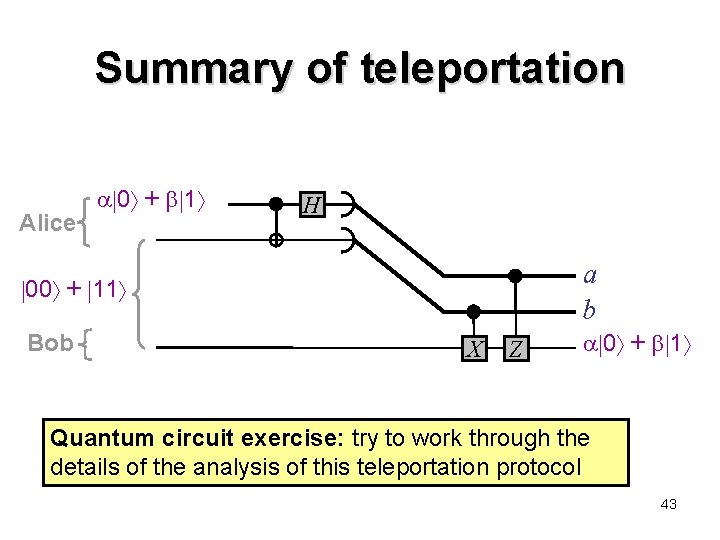
How teleportation works Initial state: ( 0 + 1 )( 00 + 11 ) (omitting the 1/ 2 factor) = 000 + 011 + 100 + 111 = ½( 00 + 11 )( 0 + 1 ) + ½( 01 + 10 )( 1 + 0 ) + ½( 00 − 11 )( 0 − 1 ) + ½( 01 − 10 )( 1 − 0 ) Protocol: Alice measures her two qubits in the Bell basis and sends the result to Bob (who then “corrects” his state) 40

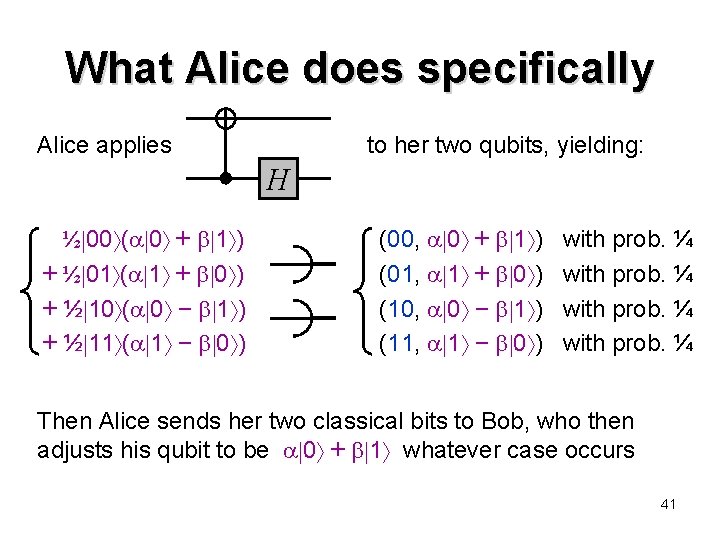
What Alice does specifically Alice applies to her two qubits, yielding: H ½ 00 ( 0 + 1 ) + ½ 01 ( 1 + 0 ) + ½ 10 ( 0 − 1 ) + ½ 11 ( 1 − 0 ) (00, 0 + 1 ) (01, 1 + 0 ) (10, 0 − 1 ) (11, 1 − 0 ) with prob. ¼ Then Alice sends her two classical bits to Bob, who then adjusts his qubit to be 0 + 1 whatever case occurs 41

Bob’s adjustment procedure Bob receives two classical bits a, b from Alice, and: if b = 1 he applies X to qubit if a = 1 he applies Z to qubit yielding: 00, 01, 0 + 1 X( 1 + 0 ) = 0 + 1 Z( 0 − 1 ) = 0 + 1 11, ZX( 1 − 0 ) = 0 + 1 10, Note that Bob acquires the correct state in each case 42

Summary of teleportation Alice 0 + 1 H a b 00 + 11 Bob X Z 0 + 1 Quantum circuit exercise: try to work through the details of the analysis of this teleportation protocol 43

No-cloning theorem 44

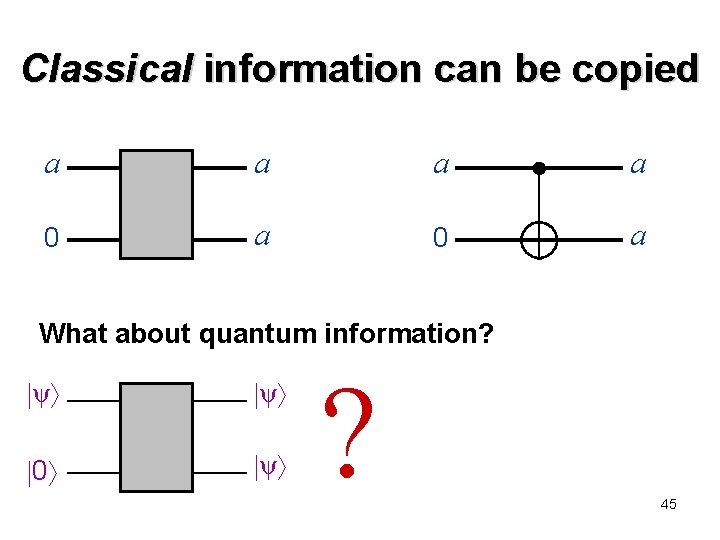
Classical information can be copied a a 0 a What about quantum information? ψ ψ 0 ψ ? 45

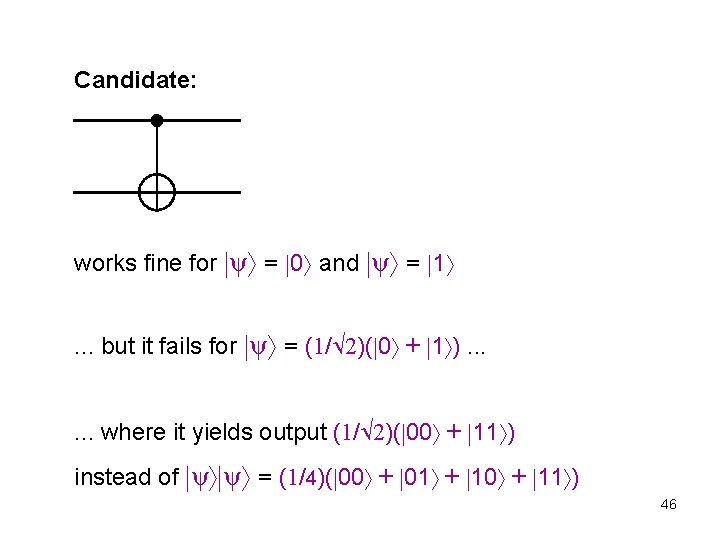
Candidate: works fine for ψ = 0 and ψ = 1 . . . but it fails for ψ = (1/ 2)( 0 + 1 ). . . where it yields output (1/ 2)( 00 + 11 ) instead of ψ ψ = (1/4)( 00 + 01 + 10 + 11 ) 46

No-cloning theorem Theorem: there is no valid quantum operation that maps an arbitrary state ψ to ψ ψ Proof: ψ 0 0 ψ Let ψ and ψ′ be two input states, yielding outputs ψ ψ g and ψ′ ψ′ g′ respectively g Since U preserves inner products: ψ U ψ ψ′ = ψ ψ′ g g′ so ψ ψ′ (1− ψ ψ′ g g′ ) = 0 so ψ ψ′ = 0 or 1 47