Introduction to Prolog Facts Questions Rules Atoms Variables

Introduction to Prolog Facts, Questions & Rules Atoms & Variables

LISP/Prolog Data n LISP/Prolog developed for AI – LISP in late 1950 s – Prolog in mid-late 1970 s Artificial Intelligence = intelligent artifact n Ability to perceive, reason and act n – LISP/Prolog concerned mostly with reasoning – Symbolic manipulation of (model of) world

Symbolic Programming n Most languages work with numbers & text – Also more complicated combinations of same n Prolog/LISP work with symbols – Also work with numbers & text – Not as suitable for numeric/textual programs n Symbols represent things in the world – Language makes it easy to use them

Prolog n PROgrammation en LOGique – PROgramming in LOGic n Logic model – Program = axioms – Execution gives theorems n Restricted logic – can’t say as much

Logic Model Proof (vs. Command) n Process n – predicate specification – predicate application n assertions questions Data – mathematical objects atoms, lists & terms

Prolog Facts n Simply state what’s true – Need to decide on symbols to state axioms n Family facts parent(mark, alex). % Mark is Alex’s parent(di, alex). % Di is Alex’s parent(bob, mark). % Bob is Mark’s parent % sign starts a comment Comment continues to end of line

Prolog Atoms mark, di, alex & bob are not variables n Atoms are themselves and nothing else n – an atom does not have a value – only one atom with any given name (no local scope, only global) n Named atoms start with lower-case letter – may contain letters (UPPER and lower case), numbers & underscores

Syntax of Prolog Facts n Consist of functor… parent – AKA name of the predicate …and arguments mark, alex n Arguments in (parentheses)… n – Right up against the functor …separated, by, commas n Ends with a period. n – Can be split over multiple lines, if you like

Syntax of Prolog Facts parent( mark, alex ). % functor % parentheses % 1 st argument % comma % 2 nd argument % period

Representations n Parenthood a relationship with two people – parent represents the relationship – mark and alex represent the people – Position distinguishes parent from child – Note: all start with lowercase letters n Arity of parenthood relationship is 2 – The predicate is parent/2 – May be other predicates with same name

Multiple Representations n Choose based on how info to be used % parent(Parent, Child) parent(mark, alex). % Mark is Alex’s parent % parents(Child, Father, Mother) parents(mark, bob, isabel). % Mark’s dad & mom are Bob And Isabel % father(Child, Parent) father(alex, mark). % Alex’s father is Mark

Exercise n Write a set of facts about your family using the second representation above. – your parents’ family if you don’t have one n My family: parents(mark, bob, isabel). parents(di, ralph, esther). parents(alex, mark, di). parents(zachary, mark, di).

Program File n A program may consist of just facts – family_1. pl n Want to start Prolog, assert the facts, and then start asking questions – We want to consult the file – Windows – double-click file to start Prolog and file is consulted automatically – Linux – need to use consult/1 predicate

Some Predicates to Start With ? - help. % general help ? - help(help). % help on … ? - apropos(help). % help available. . . ? - consult(‘family_1. pl’). % load a file ? - [‘family_1. pl’]. % ditto ? - edit(‘family_1. pl’). % edit/reload file ? - [user]. % enter facts interactively ? - halt. % exit Prolog

Asking Yes/No Questions Can ask about parentage n ? - is Prolog prompts for a question n – type in (what looks like) a fact – Prolog will tell you if it’s in the database ? - parent(mark, alex). yes ? - parent(bob, di). no

Show Prolog’s Response… parent(mark, alex). parent(di, alex). parent(bob, mark). parent(isabel, mark). parent(ralph, di). parent(esther, di). parent(franklin, bob). ? - parent(mark, alex). ? - parent(ralph, esther). ? - parent(alex, mark). ? - parent(ralph, di).

Asking Who Questions n Can also ask who is parent of whom ? - parent(Who, mark). Who = bob yes n Prolog pauses after saying who Who is – Press Enter or space to signal you’re ready – (systems differ in what keys to press)

Asking Whom Questions n Can also ask who is parent of whom ? - parent(bob, Whom). Whom = mark yes ? - parent(Who, Whom). Who = mark Whom = alex yes

Variables n Words that start with Capital Letters are variables – More accurately “unknowns” n If you ask a question with variables, Prolog says what values they could have to make what you wrote true – If there’s no such, Prolog just says no

Show Prolog’s Response… parent(mark, alex). parent(di, alex). parent(bob, mark). parent(isabel, mark). parent(ralph, di). parent(esther, di). parent(franklin, bob). ? - parent(Who, bob). ? - parent(ralph, Whom). ? - parent(alex, Whom).

Variables & No n “Closed world assumption” – if it’s not in the database, it isn’t true – everything relevant to the question is known ? - parent(garvie, franklin). no n “no” means “don’t know of any” ? - parent(Who, isabel). no

Variable Names Prolog doesn’t care about the names ? - parent(bob, X). X = mark yes use meaningful variable names ? - parent(bob, Child). X usually not good Child = mark yes ? - parent(alex, Anyone). no n

Multiple Answers n Sometimes more than one correct answer Semi-colons here mean – ? - parent(Who, alex). “are there more answers? ” Who = mark ; Who = di ; This “no” means there were no more answers no n Type a semi-colon to get next answer – n and r also work – (different systems use different characters)

Asking Anybody Questions n Start the variable with an underscore – Prolog won’t tell you its value ? - parent(mark, _Anybody). Is mark anyone’s parent (don’t care who, just whether) yes ? - parent(Parent, _Anyone). Parent = mark ; Parent = di yes Why did it say “yes” here instead of “no”? And why didn’t it find Bob?

Show Prolog’s Response… parent(mark, alex). parent(di, alex). parent(bob, mark). parent(isabel, mark). parent(ralph, di). parent(esther, di). parent(franklin, bob). ? - parent(Who, di). (show all answers) ? - parent(_Who, alex). ? - parent(alex, _Whom).

Compound Questions n Separate terms with commas – Still just one question – All things must be true, so comma = AND ? - parent(GP, P), parent(P, C). GP = bob Important Note: P = mark -- P appears twice in the question C = alex -- only gets one value yes -- same value in both places

Single Assignment n Each variable can only have one value in one answer ? - parent(GP, P), parent(P, C). n Find GP, P and C such that – GP is a parent of P, and – P is a parent of C n Variable can only have different values in different answers

Exercise n Answer these questions based on the database on pp. 1 & 2 of the text ? - parent(pam, Whom). ? - parent(tom, Whom). % give all answers ? - parent(bob, Child), parent(Child, _Any). ? - parent(Ann, jim). % careful! ? - parent(pam, Whom), parent(Who, liz). ? - parent(tom, _Any), parent(_Any, GChild).

Rules n That compound question is one we might want to ask often – Who is the grandparent of whom n New predicate: grandparent/2 – First argument is grandparent of second grandparent(GP, C) : - parent(GP, P), parent(P, C). – This is a rule, and we can put it in the file

Using Rules n Just ask the question ? - grandparent(ralph, alex). yes ? - grandparent(GP, C). GP = bob C = alex yes n Note – parent not mentioned in the answer

Understanding Rules n Consists of head and body – Head and body separated by colon-hyphen n Head is just like a fact – Tho’ it usually has variables as arguments n Body is like a question – It’s usually compound (separated by commas) n Variables connect arguments together

Rules in More Detail grandparent(GP, C) : parent(GP, P), parent(P, C). n Note the way it’s written – Indentation – Punctuation n GP is a grandparent of C if there is some P such that – GP is a parent of P, and – P is a parent of C

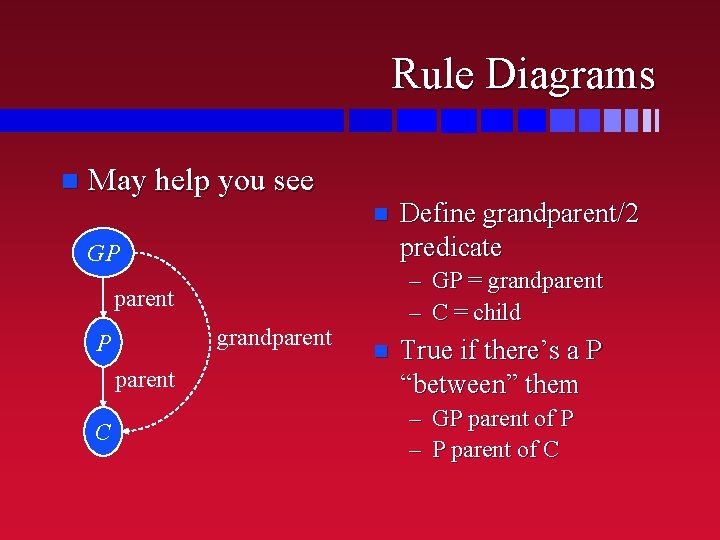
Rule Diagrams n May help you see n GP – GP = grandparent – C = child parent grandparent P parent C Define grandparent/2 predicate n True if there’s a P “between” them – GP parent of P – P parent of C

Clauses Facts and rules are called clauses n A predicate can be made up of any number of clauses n – All facts, all rules, or some of each – Usually kept together, but need not be n Looking at a predicate: ? - listing(Predicate. Name). ? - listing(Predicate. Name/Arity).

Multi-Clause Rules n Two ways to be an uncle(Uncle, Niece. Or. Nephew) : parent(Parent, Niece. Or. Nephew), brother(Uncle, Parent). Still need to define brother/2, uncle(Uncle, Niece. Or. Nephew) : sister/2 & parent(Parent, Niece. Or. Nephew), husband/2. sister(Aunt, Parent), husband(Uncle, Aunt).

Uncle Example parent(mark, alex). parent(di, alex). brother(brian, mark). sister(cathy, di). wife(susan, brian). husband(brad, cathy). ? - uncle(Who, alex). Who = brian ; Who = brad ; no

Exercise parent(mark, alex). parent(di, alex). brother(brian, mark). sister(cathy, di). wife(susan, brian). husband(brad, cathy). Who are Alex’s aunts? n Write a definition of aunt/2 n – aunt(Aunt, Nor. N).

Recursion n Predicates may be recursive – Needs a base case – fact or non-recursive rule ancestor(Anc, Desc) : Base case: your parent is your ancestor parent(Anc, Desc). ancestor(Anc, Desc) : Recursive case: an ancestor of parent(Parent, Desc), your parent is your ancestor(Anc, Parent). n Usually write base case first – more later

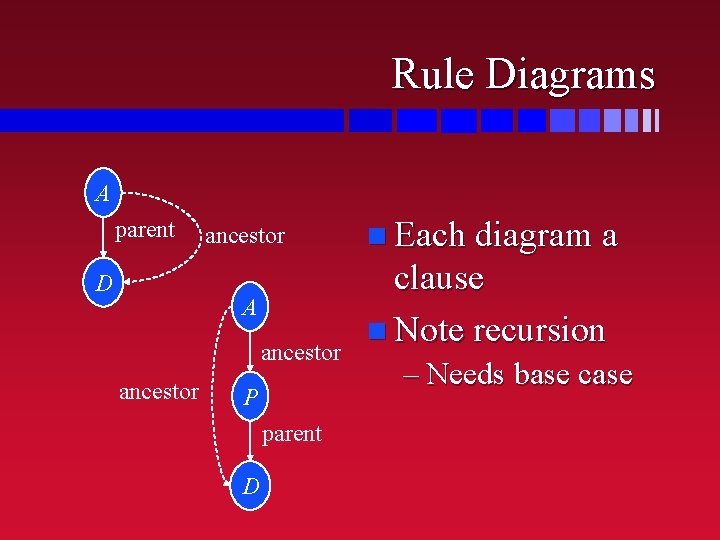
Rule Diagrams A parent D ancestor n Each diagram a A clause n Note recursion ancestor P parent D – Needs base case

Alex’s Ancestors parent(mark, alex). parent(bob, mark). parent(franklin, bob). parent(garvie, franklin). ancestor(A, D) : parent(A, D). ancestor(A, D) : parent(P, D), ancestor(A, P). ? - ancestor(Who, alex). Who = mark ; Who = bob ; Who = franklin ; Who = garvie ; no

Next Time Terms & Proof Procedures n Bratko, Chapter 2 n