Introduction to Projectile Motion Projectile calculations ball rolling

Introduction to Projectile Motion ½ Projectile calculations (ball rolling off a table) Identifying x and y components Calculating time in air, height and range
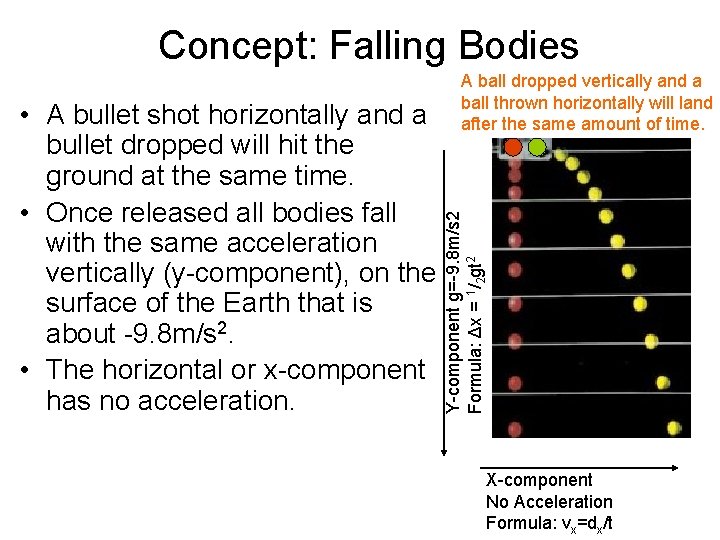
Concept: Falling Bodies Y-component g=-9. 8 m/s 2 Formula: Δx = 1/2 gt 2 • A bullet shot horizontally and a bullet dropped will hit the ground at the same time. • Once released all bodies fall with the same acceleration vertically (y-component), on the surface of the Earth that is about -9. 8 m/s 2. • The horizontal or x-component has no acceleration. A ball dropped vertically and a ball thrown horizontally will land after the same amount of time. X-component No Acceleration Formula: vx=dx/t

Concept: Horizontal and Vertical Components • Also called x and y components • X component does not have acceleration – X Equation: v=d/t or with angle cosθ*vr=d/t – X Distance is sometimes called the range – X is called the horizontal component • Y component is the height and is accelerated motion of -9. 8 m/s 2 on Earth surface. – Also called the Vertical Component – Y equations use the Kinematics Equations – Y velocity with angle: sinθ*vr

Concept: Importance of Time • Time is independent and the same for both the x and y components. • With the time both the range and the height can be calculated. • Calculating time from height or height from time can be accomplished with the following:
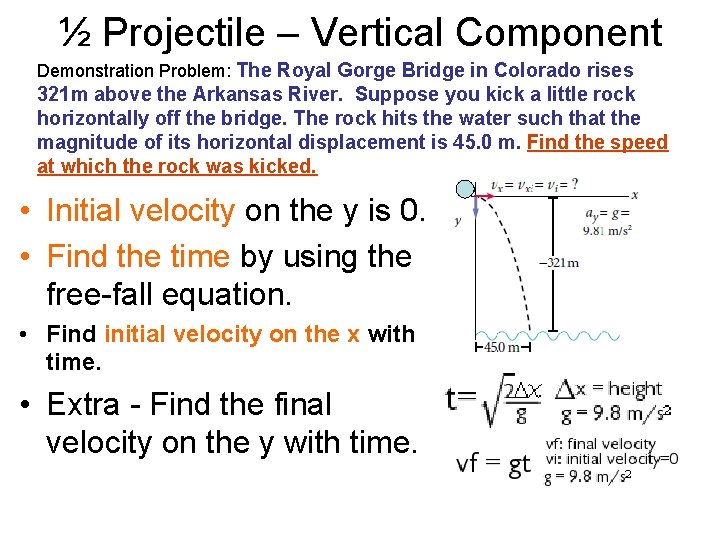
½ Projectile – Vertical Component Demonstration Problem: The Royal Gorge Bridge in Colorado rises 321 m above the Arkansas River. Suppose you kick a little rock horizontally off the bridge. The rock hits the water such that the magnitude of its horizontal displacement is 45. 0 m. Find the speed at which the rock was kicked. • Initial velocity on the y is 0. • Find the time by using the free-fall equation. • Find initial velocity on the x with time. • Extra - Find the final velocity on the y with time.
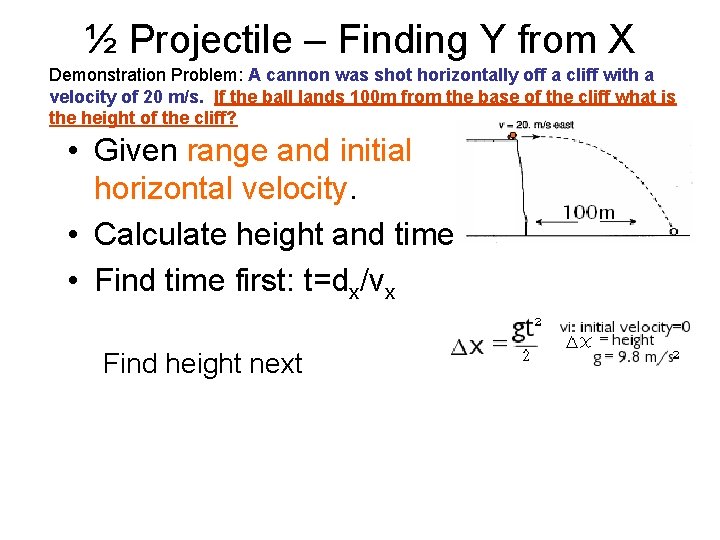
½ Projectile – Finding Y from X Demonstration Problem: A cannon was shot horizontally off a cliff with a velocity of 20 m/s. If the ball lands 100 m from the base of the cliff what is the height of the cliff? • Given range and initial horizontal velocity. • Calculate height and time. • Find time first: t=dx/vx Find height next

½ Projectile – Dropping from a Plane Demonstration Problem: A plane traveling horizontally at 100. 0 m/s at a height of 50. 0 m above the ground drops a package. What horizontal distance does the package travel before striking the ground? • Initial velocity on the y is 0. • Find the time by using the free-fall equation. • Find the range on the x with time by rearranging v=d/t to solve for d. d=v*t

Practice

Practice • During a thunderstorm, a tornado lifts a car to a height of 125 m above the ground. Increasing in strength, the tornado flings the car horizontally with an initial speed of 90. 0 m/s. How long does the car take to reach the ground? How far horizontally does the car travel before hitting the ground?

Practice 2 • A person standing at the edge of a seaside cliff kicks a stone over the edge with a speed of 18 m/s. The cliff is 52 m above the water’s surface, • How long does it take for the stone to fall to the water? With what speed does it strike the water?
- Slides: 10