Introduction to Programming for Mechanical Engineers ME 319

Introduction to Programming for Mechanical Engineers (ME 319) Lecture 3, Module 1

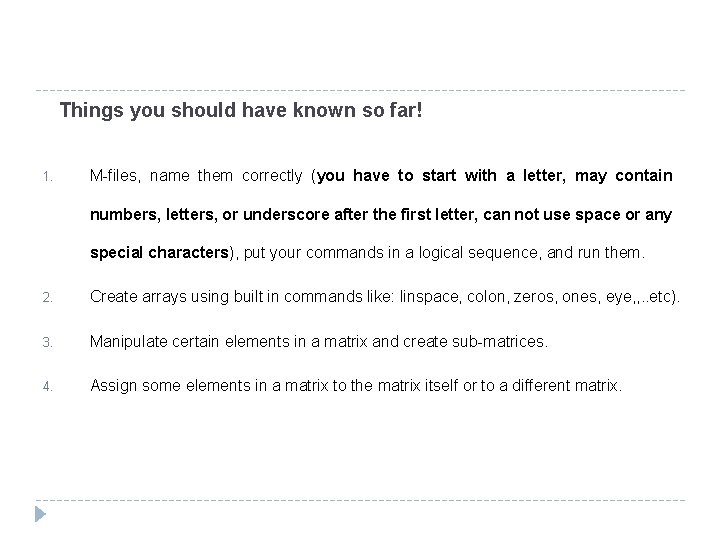
Things you should have known so far! 1. M-files, name them correctly (you have to start with a letter, may contain numbers, letters, or underscore after the first letter, can not use space or any special characters), put your commands in a logical sequence, and run them. 2. Create arrays using built in commands like: linspace, colon, zeros, ones, eye, , . . etc). 3. Manipulate certain elements in a matrix and create sub-matrices. 4. Assign some elements in a matrix to the matrix itself or to a different matrix.

Mathematical operations with arrays Examples: Addition and subtraction >> A = [1 -2 3; 2 2 3] A= 1 -2 3 2 2 3 >> B = [1 0 7; 8 -2 3] B= 1 0 7 8 -2 3 >> C = A+B C= 2 -2 10 10 0 6 % vector addition >> D = C+10 D= 12 8 20 20 10 16 % addition of vector and scalar

Mathematical operations with arrays Examples: Addition and subtraction >> D = [1 2] D= 1 2 >> E =[5 2 -7] E= 5 2 -7 >> F = [0 -3 8; 4 1 10] F= 0 -3 8 4 1 10 >> F – E ? ? ? Error using ==> minus Matrix dimensions must agree. >> E + D ? ? ? Error using ==> plus Matrix dimensions must agree. >> D (3) = 4 D= 1 2 4 >> F' - [E' D'] ans = -5 3 -5 -1 15 6 % you can’t subtract two arrays (or matrices) unless they are dimensionally equal! % adjust D dimension

Mathematical operations with arrays Examples: Addition and subtraction >> x= [1 4 8]; y=[2 1 5]; A=[3 1 6 ; 5 2 7]; >> x x= 1 4 8 >> y y= 2 1 5 >> A A= 3 1 6 5 2 7 >> A - [x; y] ans = 2 -3 -2 3 1 2 % matrices dimensions match >> A - [x' y'] ? ? ? Error using ==> minus Matrix dimensions must agree. >> 2 + A ans = 5 3 8 7 4 9 % matrices dimensions don’t match! % you can add a scalar to an array or matrix

Mathematical operations with arrays Examples: Multiplication >> A = [1 2 5; 1 1 1; -1 0 2]; B = [4 4 4; -2 0 1]; % define 1 x 3 arrays A and B >> E = A * B‘ E= 32 3 12 -1 4 4 % matrix A times transpose of B >> F = B * A F= 4 12 32 -3 -4 -8 % Matrix B times matrix A >> G = A * B ? ? ? Error using ==> mtimes Inner matrix dimensions must agree. % you can’t multiply 1 x 3 with 2 x 3

Mathematical operations with arrays Examples : Multiplication and division >> A = [1 2; 7 10] A= 1 2 7 10 >> B = [3 5; -2 0] B= 3 5 -2 0 >> A / B ans = 0. 4000 0. 1000 2. 0000 -0. 5000 % divide matrix A by matrix B using right division >> A * inv (B) ans = 0. 4000 0. 1000 2. 0000 -0. 5000 % product of A with inverse of B % So? ?

Mathematical operations with arrays Application: solving a set of equations Write it as: >> A = [3 -2 1; 2 2 -1; 3 2 5] A= 3 -2 1 2 2 -1 3 2 5 % define the coefficients matrix >> C = [-4; 9; -8] C= -4 9 -8 >> x = inv (A) * C x= 1 2 -3 >> A C ans = 1 2 -3 % define the constants vector % find the unknowns using A inverse % find the unknowns using left division

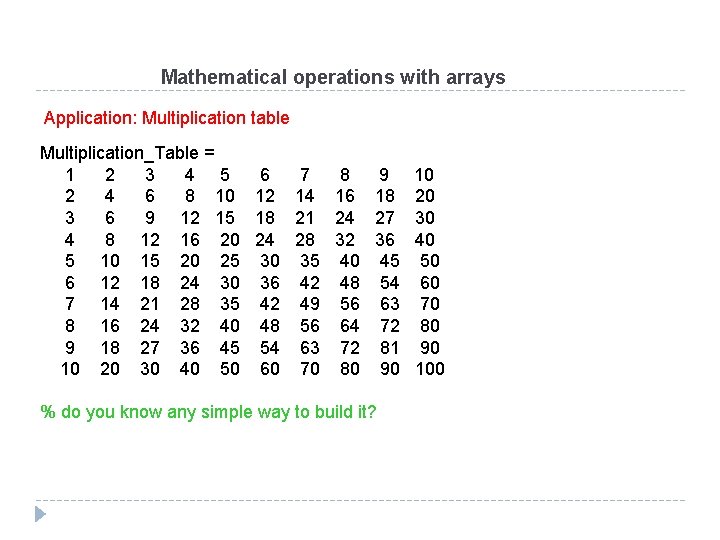
Mathematical operations with arrays Application: Multiplication table Multiplication_Table = 1 2 3 4 5 6 7 8 9 2 4 6 8 10 12 14 16 18 3 6 9 12 15 18 21 24 27 4 8 12 16 20 24 28 32 36 5 10 15 20 25 30 35 40 45 6 12 18 24 30 36 42 48 54 7 14 21 28 35 42 49 56 63 8 16 24 32 40 48 56 64 72 9 18 27 36 45 54 63 72 81 10 20 30 40 50 60 70 80 90 % do you know any simple way to build it? 10 20 30 40 50 60 70 80 90 100

Mathematical operations with arrays (Element by element) Examples: Division >> A = [5 6 -8; 0 2 4] A= 5 6 -8 0 2 4 >> B = [2 -3 8; 2 1 -2] B= 2 -3 8 2 1 -2 >> A. / B ans = 2. 5000 -2. 0000 -1. 0000 0 2. 0000 -2. 0000 % element by element division >> B = [2 -3 8; 2 1 -8] B= 2 -3 8 2 1 -8 >> B. / A Warning: Divide by zero. ans = 0. 4000 -0. 5000 -1. 0000 Inf 0. 5000 -2. 0000 % element by element division

Mathematical operations with arrays (Element by element) Examples: Multiplication >> K = [1 2 3] K= 1 2 3 >> L = [10 5 3] L= 10 5 3 >> K. ^ 4 ans = 1 16 >> L. ^ K ans = 10 25 % element by element exponentiation 81 % each element in L is raised to its corresponding power in K 27 >> M = L. ^ 2 - L. * K – L M= 80 10 -3 % mathematical expression involving matrices >> sqrt (M) ans = 8. 9443 % the use of a built-in function 3. 1623 0 + 1. 7321 i

Mathematical operations with arrays (Element by element) Examples: using the indexing pointer ‘end’ >> x =1: 7 x= 1 2 3 4 5 6 >> y = x ( 3 : end ) y= 3 4 5 6 7 % assign the x elements 3 rd till the end to an array y >> z = y ( 2 : end-1 ) z= 4 5 6 >> x ( end+1 ) = 100 x= 1 2 3 4 5 >> help end 7 % assign the y elements 2 nd till the one before the last to an array z % add an additional elemnt to x just after the last one 6 7 100

Mathematical operations with arrays (Element by element) Examples: using the indexing pointer ‘end’ >> a = [1 2 3; 4 5 6; 7 8 9; 10 11 12] a= 1 2 3 4 5 6 7 8 9 10 11 12 >> b = reshape (a, 2, 6) b= 1 7 2 8 3 9 4 10 5 11 6 12 >> c = reshape (a, 3, 4) >> d = flipud (A) >> e = fliplr (A) a= 1 4 7 10 2 3 5 6 8 9 11 12 b= 1 4 7 10 2 5 8 3 9 11 6 12

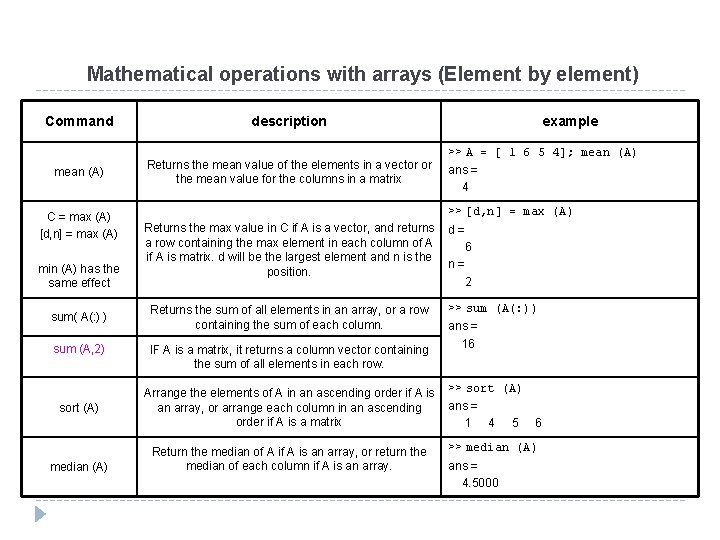
Mathematical operations with arrays (Element by element) Command mean (A) C = max (A) [d, n] = max (A) min (A) has the same effect sum( A(: ) ) sum (A, 2) sort (A) median (A) description Returns the mean value of the elements in a vector or the mean value for the columns in a matrix example >> A = [ 1 6 5 4]; mean (A) ans = 4 >> [d, n] = max (A) Returns the max value in C if A is a vector, and returns a row containing the max element in each column of A is matrix. d will be the largest element and n is the position. Returns the sum of all elements in an array, or a row containing the sum of each column. IF A is a matrix, it returns a column vector containing the sum of all elements in each row. Arrange the elements of A in an ascending order if A is an array, or arrange each column in an ascending order if A is a matrix Return the median of A is an array, or return the median of each column if A is an array. d= 6 n= 2 >> sum (A(: )) ans = 16 >> sort (A) ans = 1 4 5 6 >> median (A) ans = 4. 5000

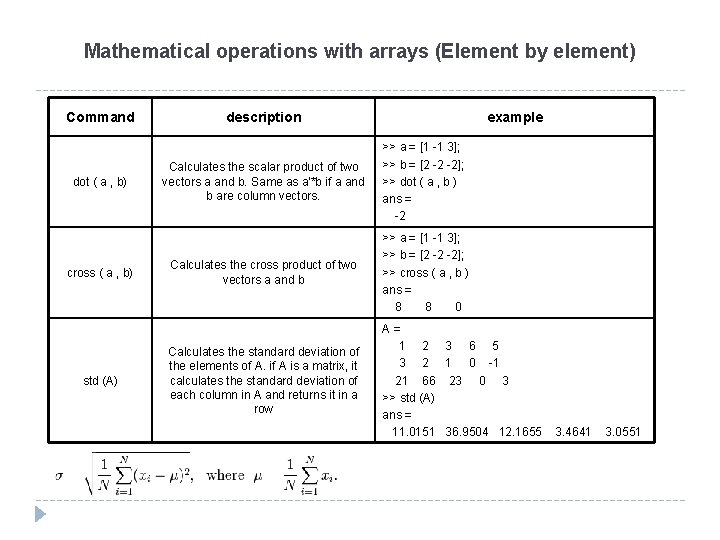
Mathematical operations with arrays (Element by element) Command dot ( a , b) cross ( a , b) std (A) description example Calculates the scalar product of two vectors a and b. Same as a'*b if a and b are column vectors. >> a = [1 -1 3]; >> b = [2 -2 -2]; >> dot ( a , b ) ans = -2 Calculates the cross product of two vectors a and b >> a = [1 -1 3]; >> b = [2 -2 -2]; >> cross ( a , b ) ans = 8 8 0 Calculates the standard deviation of the elements of A. if A is a matrix, it calculates the standard deviation of each column in A and returns it in a row A= 1 2 3 6 5 3 2 1 0 -1 21 66 23 0 3 >> std (A) ans = 11. 0151 36. 9504 12. 1655 3. 4641 3. 0551

Mathematical operations with arrays (Element by element) Command rand (n) rand (m , n) randperm (n) (b-a) * rand (m , n) + a description Generates a n x n matrix of random numbers between 0 and 1 example >> rand (2) ans = 0. 9501 0. 6068 0. 2311 0. 4860 Generates a m x n matrix of random numbers between 0 and 1 >> rand (1, 3) ans = 0. 8913 0. 7621 0. 4565 Generates a row vector of n elements that are random permutation of integers 1 through n >> randperm (5) ans = 4 5 3 1 2 Generates a m x n matrix of random numbers between a and b >> (12 - 4) * rand (2, 3) + 4 ans = 11. 4838 7. 2822 4. 4631 11. 3352 11. 1492 6. 8229