Introduction to probability Stat 134 FAll 2006 Berkeley

Introduction to probability Stat 134 FAll 2006 Berkeley Lectures prepared by: Elchanan Mossel Yelena Shvets Follows Jim Pitman’s book: Probability Sections 1. 1 -1. 3 9/9/2020

Probability as Proportion Suppose there are 20 people taking Stat 134. There are 7 ? ? ? ? ? & 13 What is the chance that a person selected at random from the class is a woman ? 9/9/2020

Probability as Proportion What is the chance that a word from this sentence begins with a w? 4 What with w word 14 10 chance is from that this a the begins a sentence 9/9/2020

Space of outcomes The space of all possible outcomes will be denoted by W. 9/9/2020

Probability as Proportion If W is finite and each outcome is equally likely than the probability of an event A is: 9/9/2020

Probability as Proportion Suppose there are 20 people taking Stat 134. There are 7 ? ? ? ? ? & 13 What is the chance that a person selected at random from the class is a woman ? 9/9/2020
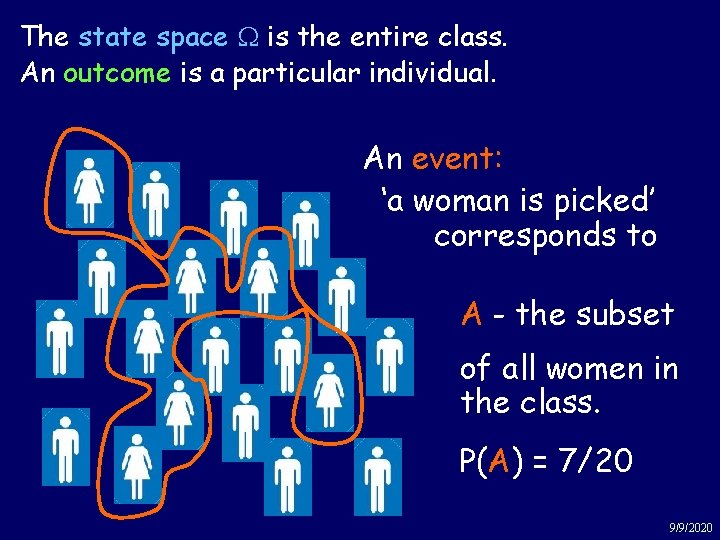
The state space W is the. Men entire. Women class. Example: An outcome is a particular individual. An event: ‘a woman is picked’ corresponds to A - the subset of all women in the class. P(A) = 7/20 9/9/2020

Probability as Proportion What is the chance that a word from this sentence begins with a w? 4 What with w word 14 10 chance is from that this a the begins a sentence 9/9/2020

The state space W is. Words the (setin ofawords of the ) Example: sentence. An outcome is a particular word. An event: ‘a word starts with w’ corresponds to set A of all the words starting with w. A What with w word P(A) = 4/14 W chance is from that this a the begins a sentence 9/9/2020

Roll two dice. 10 What is the chance that the sum is: Equal to 7? Equal to 2? Even? Odd? First we need a Sample Space. Is W = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} ? Problem: are events in W equally likely? 9/9/2020

Roll two dice. 11 What is the chance that the sum is: Equal to 7? Equal to 2? Even? Odd? 2 3 The correct sample space W: 4 5 6 7 3 4 5 6 7 8 9 10 11 7 8 9 10 11 12 9/9/2020

Roll two dice. Example: Sum of two What is the chance that the sum is: Equal to 7? Equal to 2? Even? Odd? 2 3 6/36 = 1/6 dice 4 5 6 77 3 4 5 6 77 8 9 10 11 77 8 9 10 11 12 9/9/2020

Roll two dice. Example: Sum of two What is the chance that the sum is: Equal to 7? Equal to 2? Even? Odd? 22 3 1/36 dice 4 5 6 7 3 4 5 6 7 8 9 10 11 7 8 9 10 11 12 9/9/2020

Roll two dice. Example: Sum of two dice What is the chance that the sum is: Equal to 7? Equal to 2? Even? Odd? 22 3 44 5 18/36 = 1/2 66 7 3 44 5 66 7 88 9 10 10 11 7 88 9 10 10 11 12 12 9/9/2020

Roll two dice. Example: Sum of two dice What is the chance that the sum is: Equal to 7? Equal to 2? Even? Odd? 22 3 44 5 18/36 = 1/2 66 7 3 44 5 66 7 88 9 10 10 11 7 88 9 10 10 11 12 12 9/9/2020
Probability interpretation: as frequency in population. • In a population we interpret the probability of an event as the proportion of the event in the population. • The census is based on the assumption that if we take a large enough sample then the observed frequency of an event at the sample should be close to the probability of the event in the population. 9/9/2020

Probability Interpretation as frequency in repeated experiments • Repeating the same experiment over and over again, the observed frequency of experiments ending at an event A should be close to P(A). • The fact that the observed frequencies converge to P(A) is called the law of large numbers. We will prove this law later. 9/9/2020

Events & Subsets event: a possible outcome subset: outcome space W Venn diagram P(W) =1 9/9/2020

Events & Subsets event: impossible outcome – subset: empty set Æ Venn diagram P(Æ) =0 9/9/2020

Events & Subsets event: outcome belongs to A – subset: A of W Venn diagram A W 0 · P(A) · 1 9/9/2020

Events & Subsets event: outcome is not in A – subset: complement of A in W Venn diagram AC P(Ac) = 1 -P(A) 9/9/2020

Events & Subsets event: outcome belongs to A and B – subset: AB of W Venn diagram P(AB) ¸ 0 A B P(AB) · P(A) P(AB) · P(B) 9/9/2020

Events & Subsets event: outcome belongs to A or B – subset: A[B of W Venn diagram A A B P(A[B) ¸ P(A) P(A[B) ¸ P(B) P(A[B) = P(A) + P(B) - P(AB) 9/9/2020

Events & Subsets event: outcome belongs to A but not to B – subset: AB of W Venn diagram A B P(AB) = P(A) – P(AÅB) 9/9/2020

Events & Subsets event: outcome is in A or C with A and C mutually exclusive subset: disjoint union of A and C Venn diagram A C P(At. C)=P(A) + P(C) Note: AÅC = Æ 9/9/2020

Events & Subsets Event interpretation : if an outcome is in A then it must be in D Subset interpretation: A ½ D Venn diagram P(A)· P(D) A D Note: AÅD = A 9/9/2020

Partition If B 1 t B 2 t … t Bn = B We say that B is partitioned into n mutually exclusive events B 1, B 2, …, Bn. B 1 B 4 B 3 B 2 Bn Bn-1 9/9/2020

Rules of Probability • Non-negative: P(B) ¸ 0 for all BµW. • Additive: if B = B 1 t B 2 t … t Bn then P(B) = P(B 1) + P(B 2) + … + P(Bn). • Sums to 1: P(W) = 1 A distribution over W is a function P on subsets of W which satisfies these three rules. 9/9/2020

Example: Rich & Famous In a certain town 10% of the inhabitants are rich, 5% are famous and 3% are rich and famous. Famous Neither Rich 9/9/2020
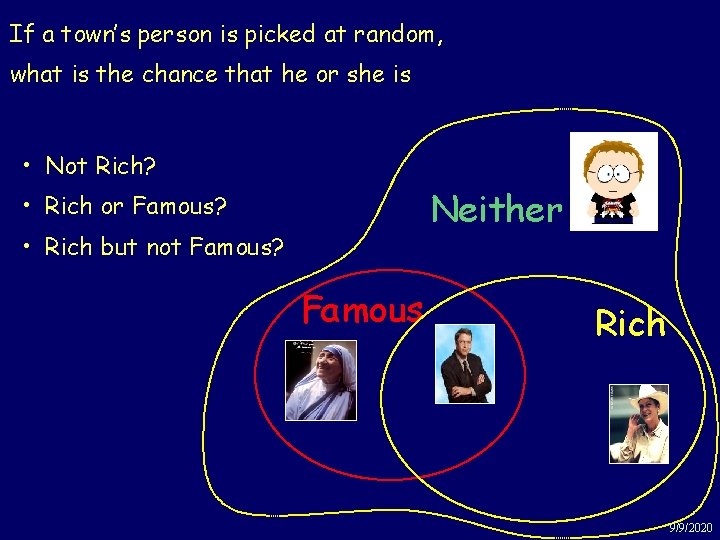
If a town’s person is picked Rich at random, Example: & Famous what is the chance that he or she is • Not Rich? Neither • Rich or Famous? • Rich but not Famous? Famous Rich 9/9/2020
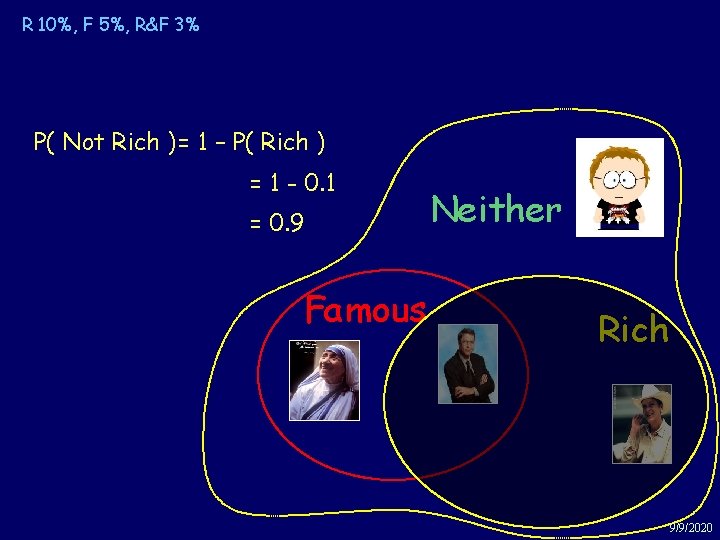
R 10%, F 5%, R&F 3% Example: Rich & Famous P( Not Rich )= 1 – P( Rich ) = 1 - 0. 1 = 0. 9 Famous Neither Rich 9/9/2020

R 10%, F 5%, R&F 3% Example: Rich & Famous P( Rich or Famous) = P(Rich) + P (Famous) - P( Rich & Famous) = 0. 1 + 0. 05 - 0. 03 = 0. 12 Famous Rich 9/9/2020

R 10%, F 5%, R&F 3% Example: Rich & Famous P( Rich but not famous) = P(Rich) – P( Rich &Famous) = 0. 1 -0. 03 = 0. 07 Famous Rich 9/9/2020

Similar. Example: computations enable us to complete Rich & Famous the following distribution table: Not Rich Famous Not Famous 0. 02 0. 03 0. 07 Not Rich Not Famous 0. 88 We can use this table to construct a histogram… 9/9/2020
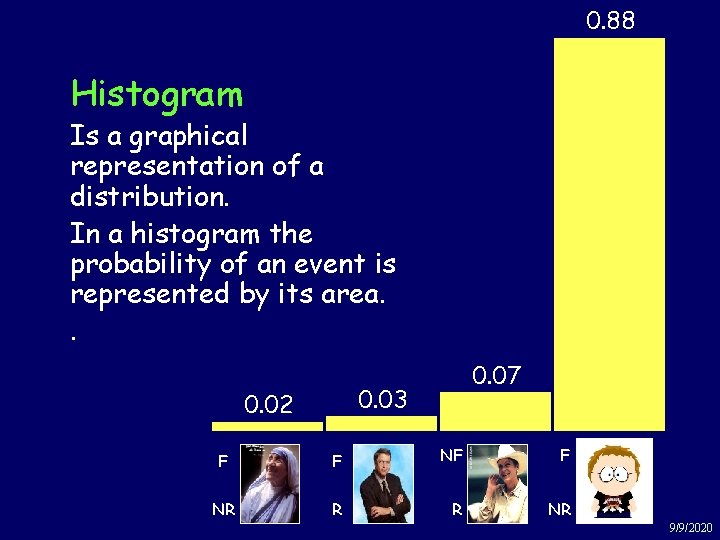
0. 88 Example: Rich & Famous Histogram Is a graphical representation of a distribution. In a histogram the probability of an event is represented by its area. . 0. 07 0. 03 0. 02 F F NR R R NR 9/9/2020

Example: Numbered tickets 1 1 3 2 5 4 6 6 Draw one ticket uniformly at random. What is the chance that the number is greater than 3? 9/9/2020

Example: tickets Here is the. Numbered distribution table: 1 2 3 4 5 6 ¼ 1/8 1/8 ¼ 9/9/2020

Example: Numbered tickets Now let’s build a histogram: 1/4 1/8 1/8 1/8 2 3 4 5 6 9/9/2020

Example: Numbered tickets Let’s find the chance that the number on the ticket is greater than 3: 1/4 1/8 1/8 1/8 2 3 4 5 6 1/8 + 1/4 = 1/2 9/9/2020
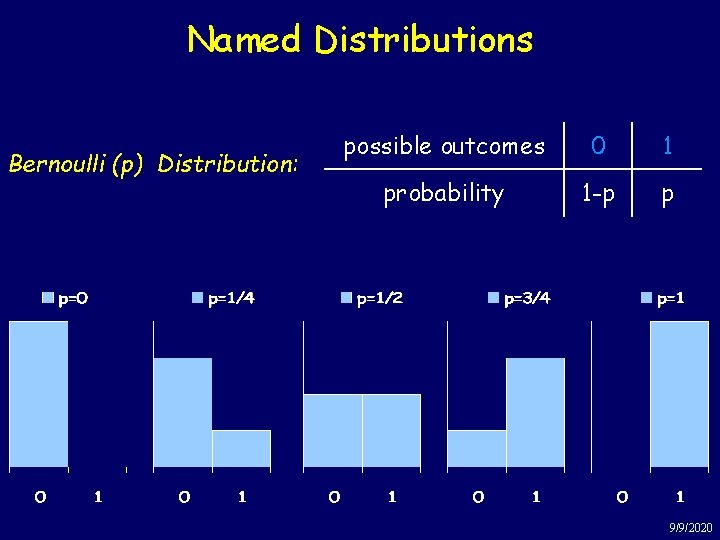
Named Distributions Bernoulli (p) Distribution: possible outcomes 0 1 probability 1 -p p 9/9/2020
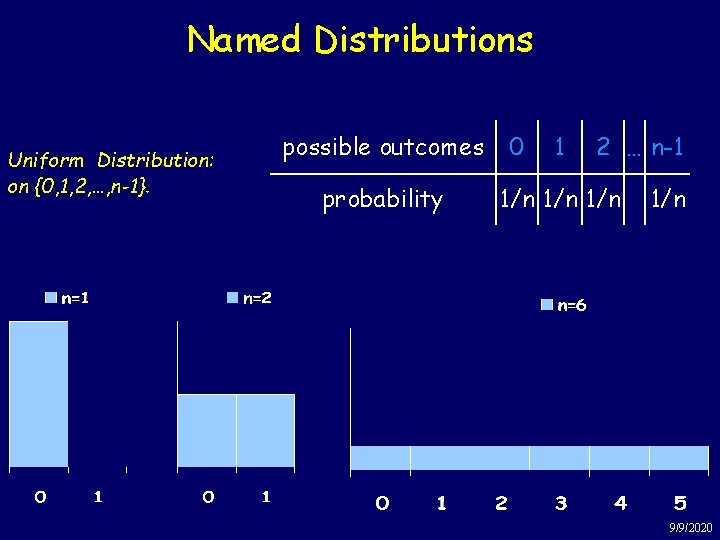
Named Distributions Uniform Distribution: on {0, 1, 2, …, n-1}. possible outcomes probability 0 1 2 … n-1 1/n 1/n 9/9/2020
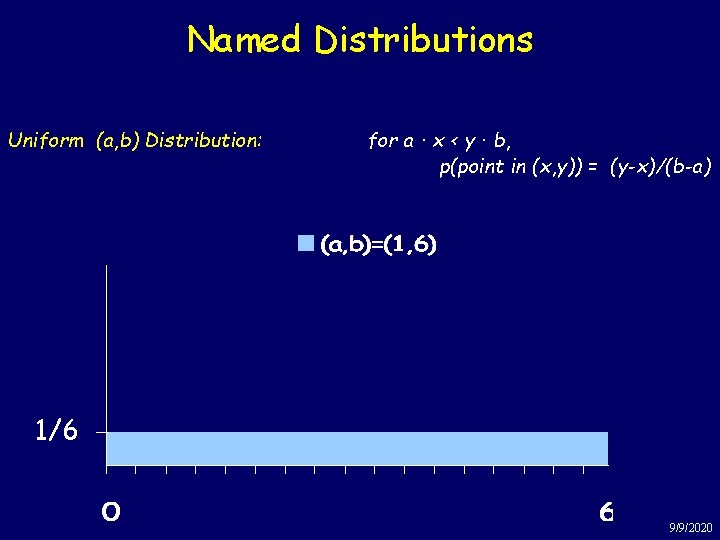
Named Distributions Uniform (a, b) Distribution: for a · x < y · b, p(point in (x, y)) = (y-x)/(b-a) 1/6 9/9/2020

Named Distributions Uniform (a, b) Distribution: c) for (x, y)2 B ½ (a, b)£ (c, d) p(point in (x, y)) = Area(B)/((b-a)(d- (a, b)x(c, d) = (0, 6)x(0, 1) 1/6 9/9/2020
- Slides: 43