INTRODUCTION to PROBABILITY prob 1 BASIC CONCEPTS of

INTRODUCTION to PROBABILITY prob 1

BASIC CONCEPTS of PROBABILITY Experiment p Outcome p Sample Space n. Discrete n. Continuous p Event p prob 2

Interpretations of Probability Mathematical p Empirical p Subjective p prob 3

MATHEMATICAL PROBABILITY P(E) = prob 4

PROPERTIES p 0 < P(E) < 1 p P(E’) = 1 - P(E) p P(A or B) = P(A) + P(B) for two events, A and B, that do not intersect prob 5

Example A part is selected for testing. It could have been produced on any one of five cutting tools. p. What is the probability that it was produced by the second tool? p. What is the probability that it was produced by the second or third tool? p. What is the probability that it was not produced by the second tool? prob 6

INDEPENDENT EVENTS p Events A and B are independent events if the occurrence of A does not affect the probability of the occurrence of B. p If A and B are independent P(A and B) = P(A)*P(B) prob 7

Example The probability that a lab specimen is contaminated is 0. 05. Two samples are checked. p p What is the probability that both are contaminated? What is the probability that neither is contaminated? prob 8

DEPENDENT EVENTS Events A and B are dependent events if they are not independent. p If A and B are independent p P(A and B) = P(A)*P(B/A) prob 9

Example From a batch of 50 parts produced from a manufacturing run, two are selected at random without replacement? What is the probability that the second part is defective given that the first part is defective? prob 10

MUTUALLY EXCLUSIVE EVENTS Events A and B are mutually exclusive if they cannot occur concurrently. If A and B are mutually exclusive, P(A or B) = P(A) + P(B) prob 11

NON MUTUALLY EXCLUSIVE EVENTS If A and B are not mutually exclusive, P(A or B) = P(A) + P(B) - P(A and B) prob 12

Example Disks of polycarbonate plastic from a supplier are analyzed for scratch resistance and shock resistance. For a disk selected at random, what is the probability that it is high in shock or scratch resistance? Scratch R high low Shock Resistance high low 80 9 6 5 prob 13

RANDOM VARIABLES Discrete p Continuous p prob 14

DISCRETE RANDOM VARIABLES Maps the outcomes of an experiment to real numbers p The outcomes of the experiment are countable. p Examples n n Equipment Failures in a One Month Period Number of Defective Castings prob 15

CONTINUOUS RANDOM VARIABLE Possible outcomes of the experiment are represented by a continuous interval of numbers Examples • • • force required to break a certain tensile specimen volume of a container dimensions of a part prob 16

Discrete RV Example A part is selected for testing. It could have been produced on any one of five cutting tools. The experiment is to select one part. • • • Define a random variable for the experiment. Construct the probability distribution. Construct a cumulative probability distribution. prob 17

EXPECTED VALUE Discrete Random Variable E(X) = X 1 P(X 1) + …. + Xn. P(Xn) prob 18

Example At a carnival, a game consists of rolling a fair die. You must play $4 to play this game. You roll one fair die, and win the amount showing (e. g. . . if you roll a one, you win one dollar. ) If you were to play this game many times, what would be your expected winnings? Is this a fair game? prob 19

CUMULATIVE PROBABILITY FUNCTIONS For a discrete random variable X, the cumulative function is: F(X) = P(X < x) = S f(z) for all z < x prob 20
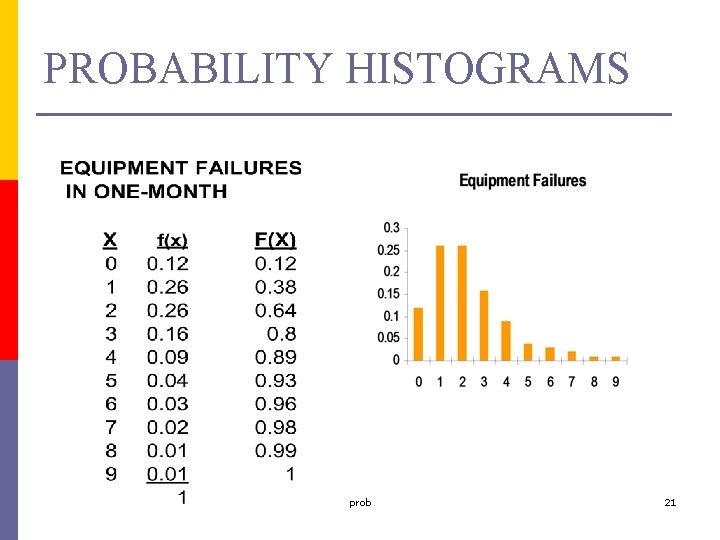
PROBABILITY HISTOGRAMS prob 21
![Variance of a Discrete Probability Distribution Var(X) = S[x - E(X)]2*f(x) prob 22 Variance of a Discrete Probability Distribution Var(X) = S[x - E(X)]2*f(x) prob 22](http://slidetodoc.com/presentation_image_h/961eb44d1ae6caa4c379121947b91bff/image-22.jpg)
Variance of a Discrete Probability Distribution Var(X) = S[x - E(X)]2*f(x) prob 22

SOME SPECIAL DISCRETE RV’s Binomial p Poisson p Geometric p Hypergeometric p prob 23

BINOMIAL X = the number of successes in n independent Bernoulli trials of an experiment f(x) = n. Cxpx(1 -p)n-x for x = 0, 1, 2…. n f(x) = 0 otherwise prob 24

EXAMPLE A manufacturer claims only 10% of his machines require repair within one year. If 5 of 20 machines require repair, does this support or refute his claim? ? prob 25

POISSON DISTRIBUTION X = # of success in an interval of time, space, distance f(x) = e-l lx/x! f(x) = 0 for x = 0, 1, 2, …. . . otherwise prob 26

EXAMPLES Examples of the Poisson • • • number of messages arriving for routing through a switching center in a communications network number of imperfections in a bolt of cloth number of arrivals at a retail outlet prob 27

EXAMPLE of POISSON The inspection of tin plates produced by a continuous electrolytic process. Assume that the number of imperfections spotted per minute is 0. 2. p Find the probability of no more than one imperfection in a minute. p Find the probability of one imperfection in 3 minutes. prob 28

GEOMETRIC DISTRIBUTION X = # of trials until the first success f(x) = px(1 -p)n-x f(x) = 0 for x = 0, 1, 2…. n otherwise prob 29

Example of Geometric The probability that a measuring device will show excessive drift is 0. 05. A series of devices is tested. What is the probability that the 6 th device will show excessive drift? Find the probability of the 1 st drift on the 6 th trail. P(X=1) = (0. 05)(0. 95)5 = 0. 039 prob 30
- Slides: 30