Introduction to Probabilistic Sequence Models Theory and Applications

Introduction to Probabilistic Sequence Models: Theory and Applications David H. Ardell, Forskarassistent

Lecture Outline: Intro. to Probabilistic Sequence Models Motif Representations: Consensus Sequences, Motifs and Blocks, Regular Expressions Probabilistic Sequence Models: profiles, HMMs, SCFG

Consensus sequences revisited Consense sequences make poor summaries A T C G

A motif is a short stretch of protein sequence associated with a particular function (R. Doolittle, 1981) The first described, and most prominent example is the P-loop that binds phosphate in ATP/GTP-binding proteins [GA]x(4)GK[ST] A variety of databases of such motifs exist: such as BLOCKS, PROSITE, and PRINTS, and there are many tools to search proteins for matches to blocks.

Introduction to Regular Expressions (Regexes) Regular Expressions specify sets of sequences that match a pattern. Ex: a[bc]a matches "aba" and "aca" In addition to literals like a and b in the last example, regular expressions provide quantifiers like * (0 or more), + (1 or more), ? (0 or 1) and {N, M} (between N and M): Ex: a[bc]*a matches "aa", "aba", "acca", "acbcba" etc As well as grouping constructions like character classes [xy], compound literals like (this)+, and logical relations, like | which means "or" in (this|that) Anchors match the beginning ^ and end $ of strings

IUPAC DNA ambiguity codes as reg-ex classes Pyrimidines Pu. Rines Strong Weak Keto a. Mino B D H V Any base Y R S W K M B D H V N = = = [CT] [AG] [CG] [AT] [GT] [AC] [CGT] (one letter greater than A=not-A) [AGT] [ACG] [ACGT]

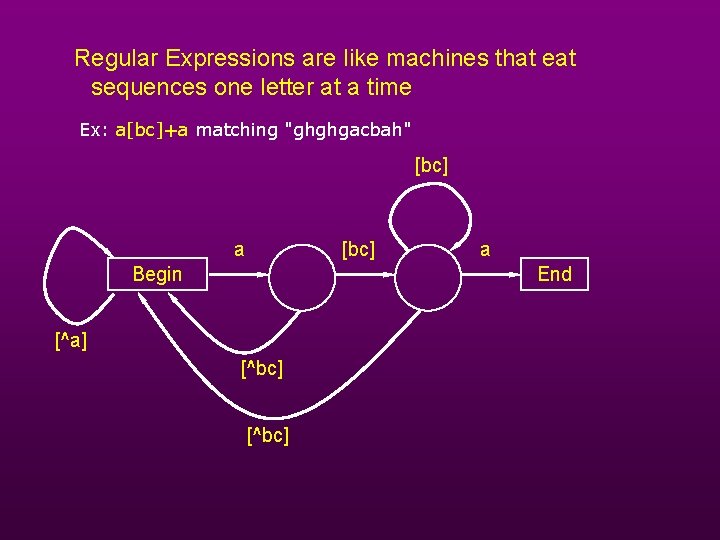
Regular Expressions are like machines that eat sequences one letter at a time Ex: a[bc]+a matching "ghghgacbah" [bc] a [bc] Begin a End [^a] [^bc]

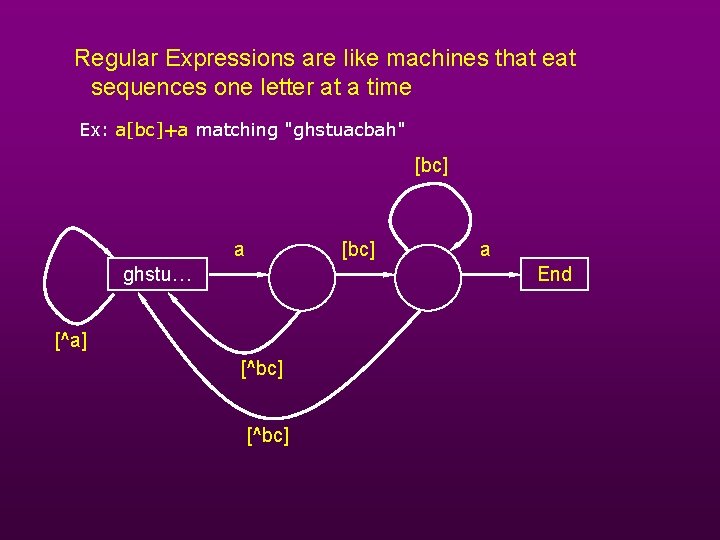
Regular Expressions are like machines that eat sequences one letter at a time Ex: a[bc]+a matching "ghstuacbah" [bc] a [bc] ghstu… a End [^a] [^bc]

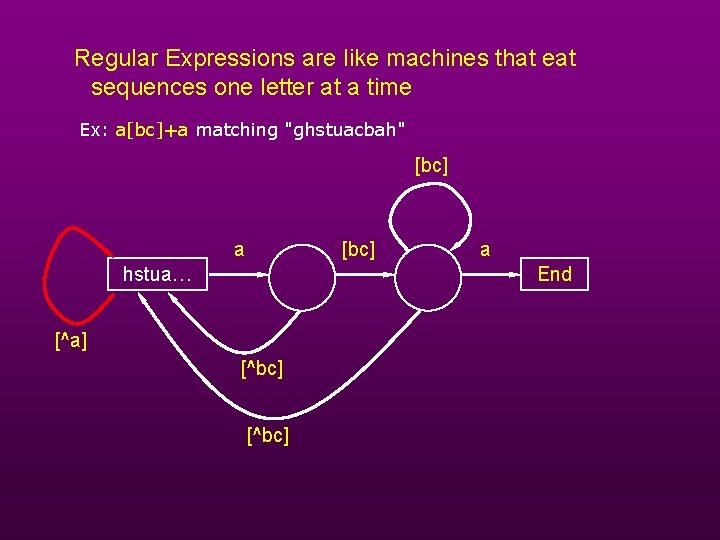
Regular Expressions are like machines that eat sequences one letter at a time Ex: a[bc]+a matching "ghstuacbah" [bc] a [bc] hstua… a End [^a] [^bc]

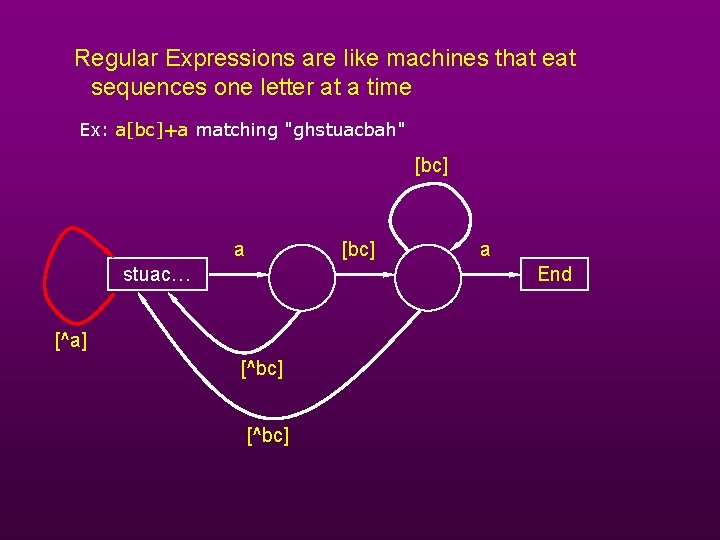
Regular Expressions are like machines that eat sequences one letter at a time Ex: a[bc]+a matching "ghstuacbah" [bc] a [bc] stuac… a End [^a] [^bc]

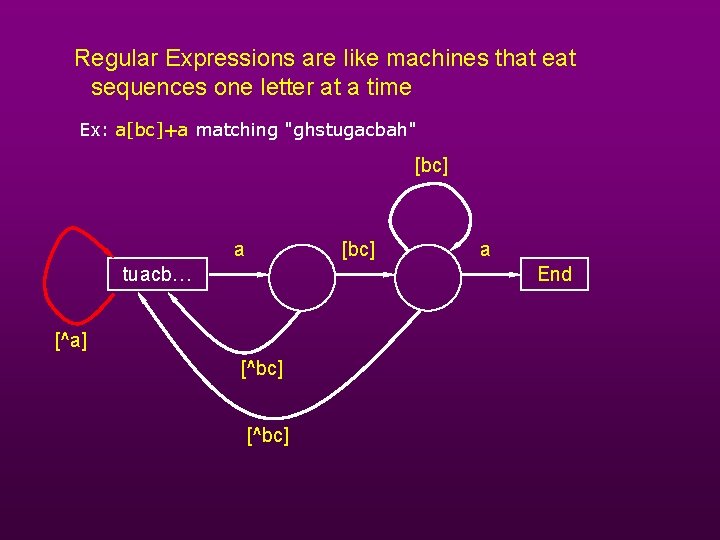
Regular Expressions are like machines that eat sequences one letter at a time Ex: a[bc]+a matching "ghstugacbah" [bc] a [bc] tuacb… a End [^a] [^bc]

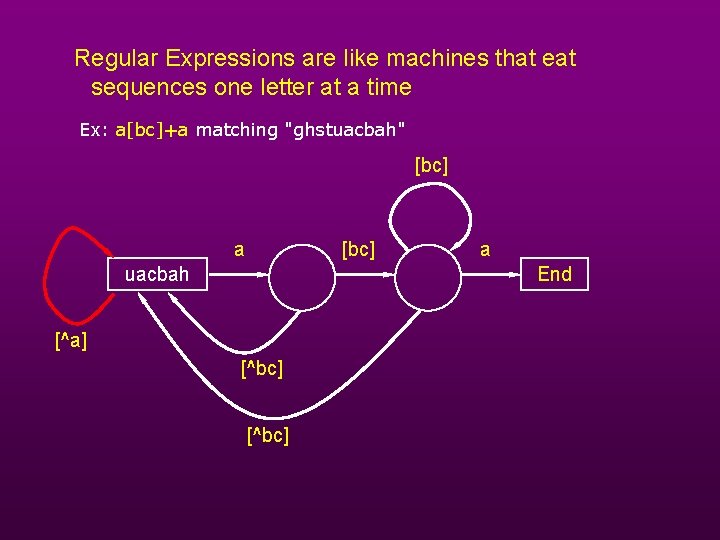
Regular Expressions are like machines that eat sequences one letter at a time Ex: a[bc]+a matching "ghstuacbah" [bc] a [bc] uacbah a End [^a] [^bc]

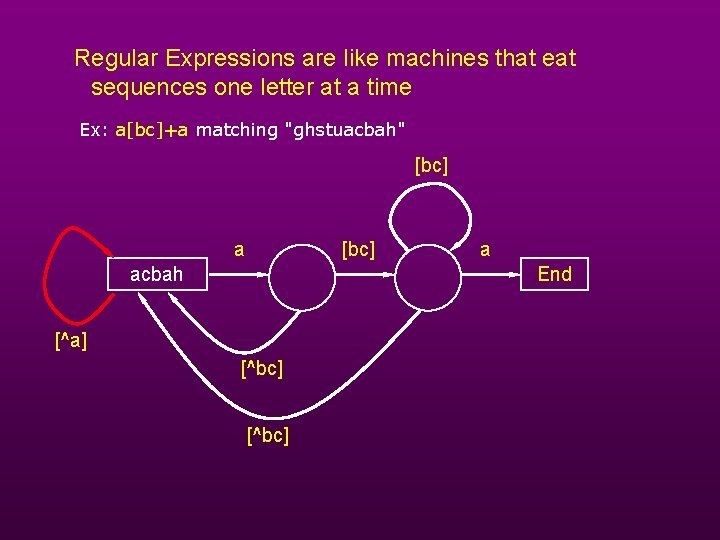
Regular Expressions are like machines that eat sequences one letter at a time Ex: a[bc]+a matching "ghstuacbah" [bc] acbah a End [^a] [^bc]

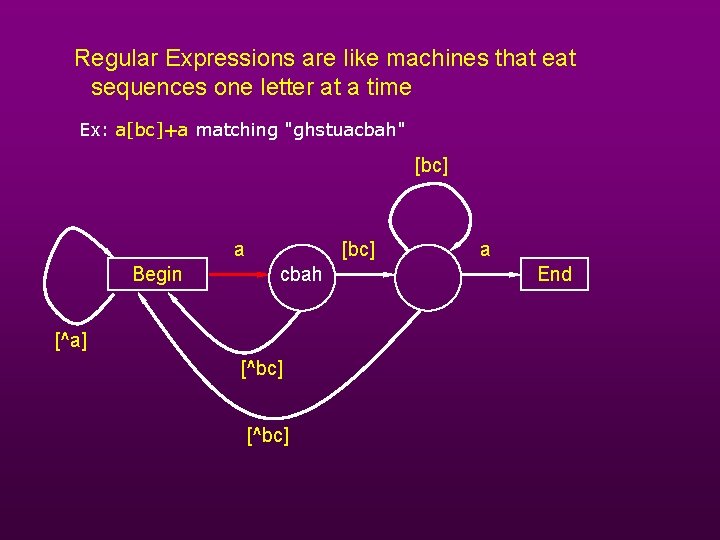
Regular Expressions are like machines that eat sequences one letter at a time Ex: a[bc]+a matching "ghstuacbah" [bc] a Begin [bc] cbah [^a] [^bc] a End

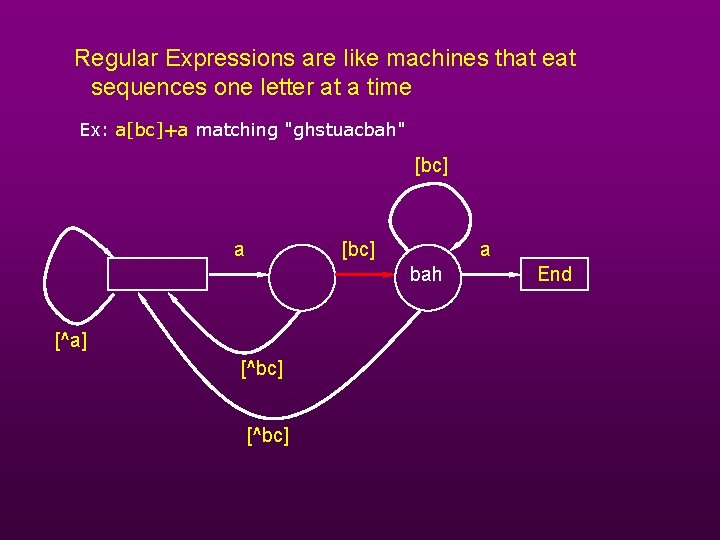
Regular Expressions are like machines that eat sequences one letter at a time Ex: a[bc]+a matching "ghstuacbah" [bc] a bah [^a] [^bc] End

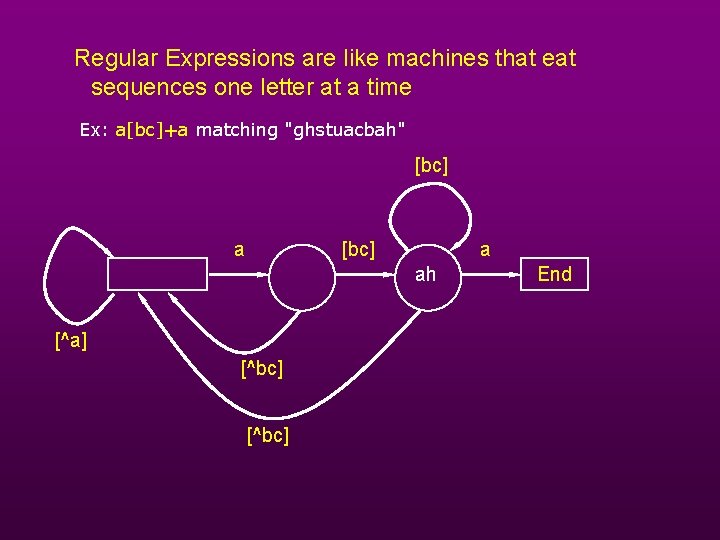
Regular Expressions are like machines that eat sequences one letter at a time Ex: a[bc]+a matching "ghstuacbah" [bc] a ah [^a] [^bc] End

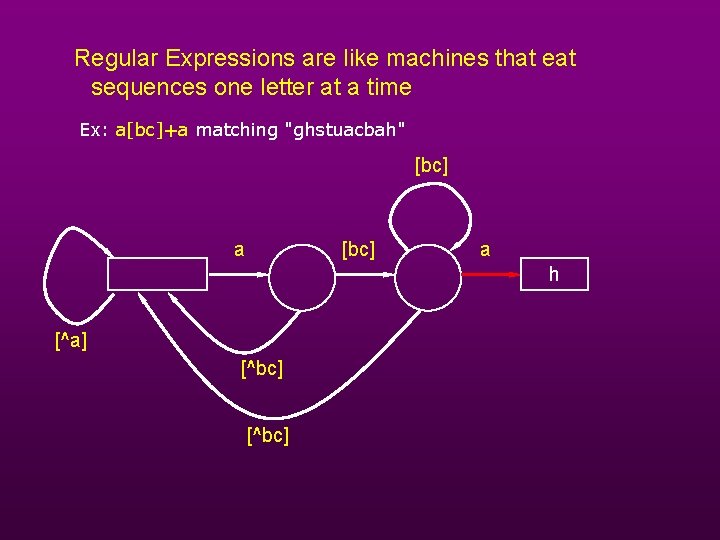
Regular Expressions are like machines that eat sequences one letter at a time Ex: a[bc]+a matching "ghstuacbah" [bc] a h [^a] [^bc]

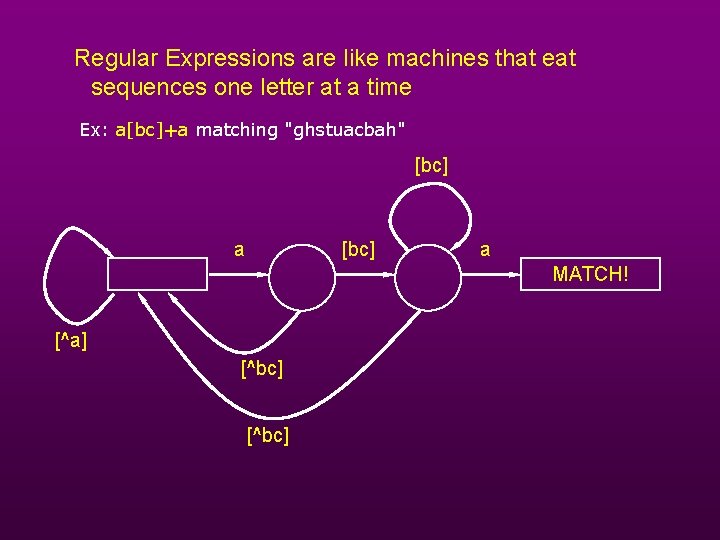
Regular Expressions are like machines that eat sequences one letter at a time Ex: a[bc]+a matching "ghstuacbah" [bc] a MATCH! [^a] [^bc]

Motifs are almost always either too selective or too specific The first described, and most prominent example is the P-loop that binds phosphate in ATP/GTP-binding proteins [GA]x(4)GK[ST] Prob. of this motif ≈ (1/10)(1/20)(1/10) = 0. 000025 Expected number of matches in database with 3. 2 x 108 residues: about 8000! About half of the proteins that match this motif are not NTPases of the P-loop class. (Lack of specificity)

Motifs are almost always either too selective or too specific [GA]x(4)GK[ST] Larger and larger alignments of true members of the class give more and more exceptions to the rule (lack of sensitivity) Extending the rule ([GAT]x(4)[GAF][KTL][STG]) leads to loss of specificity

A better way to model motifs REGULAR EXPRESSIONS “(TTR[ATC]WT) N{15, 22} (TRWWAT)” Can find alternative members of a class Treat alternative character states as equally likely. Treat all spacer lengths as equally likely. PROFILES (Position-Specific Score Matrices)

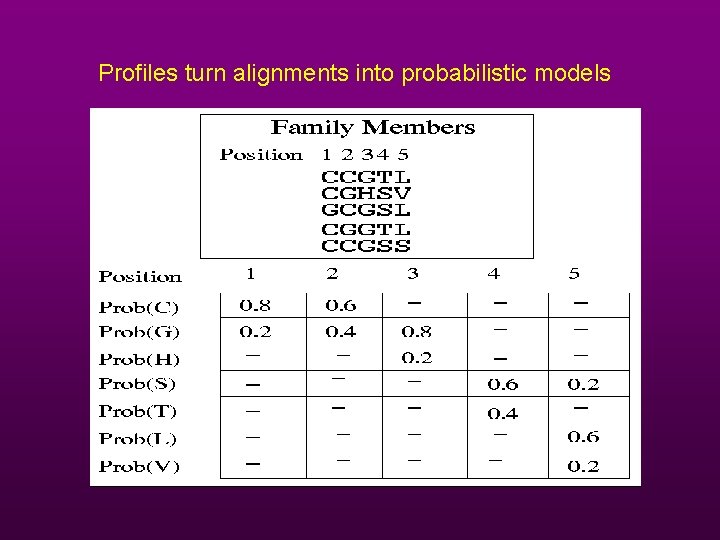
Profiles turn alignments into probabilistic models

A graphical view of the same profile: CCGTL… CGHSV… GCGSL… CGGTL… CCGSS… H C C G G G T M L S S …

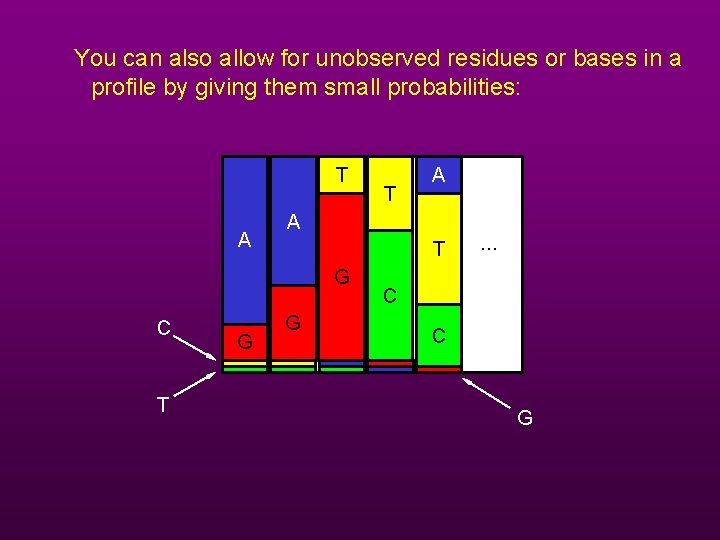
You can also allow for unobserved residues or bases in a profile by giving them small probabilities: T A A T G C T G T A G … C C G

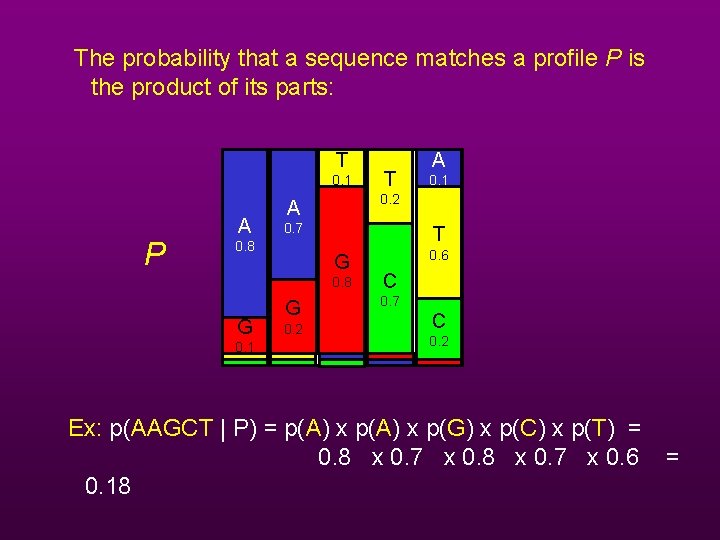
The probability that a sequence matches a profile P is the product of its parts: T 0. 1 P A 0. 7 T G 0. 8 0. 1 G 0. 2 0. 1 0. 2 A 0. 8 G T A 0. 6 C 0. 7 C 0. 2 Ex: p(AAGCT | P) = p(A) x p(G) x p(C) x p(T) = 0. 8 x 0. 7 x 0. 6 = 0. 18

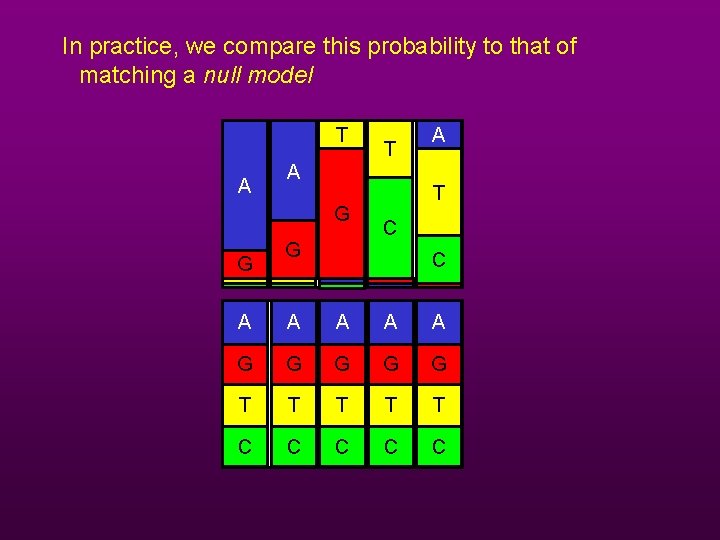
In practice, we compare this probability to that of matching a null model T A A G G T G A T C C A A A G G G T T T C C C

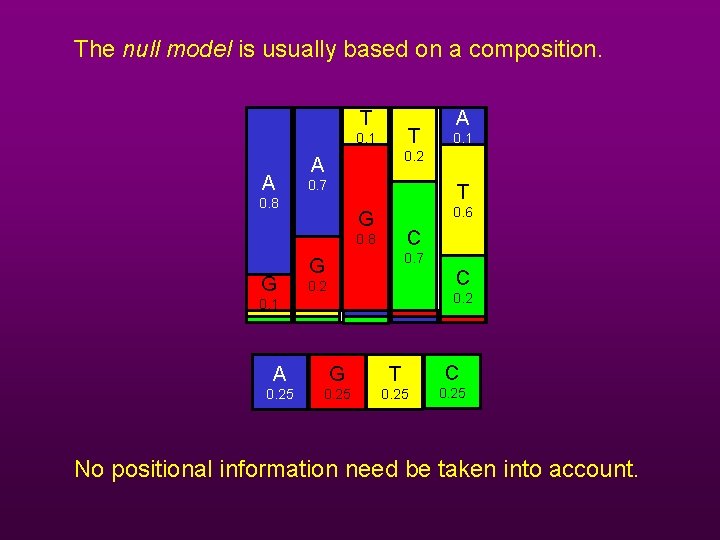
The null model is usually based on a composition. T T 0. 1 A 0. 1 0. 2 A 0. 7 T 0. 8 0. 6 G C 0. 8 G A 0. 7 G C 0. 2 0. 1 A G T C 0. 25 No positional information need be taken into account.

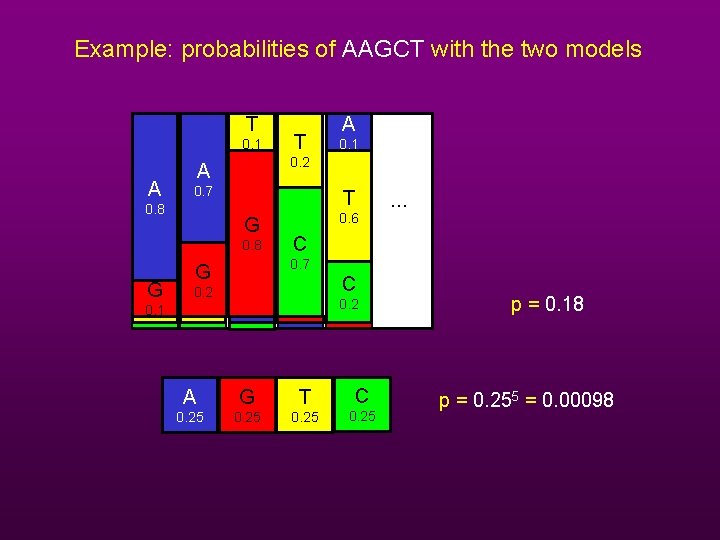
Example: probabilities of AAGCT with the two models T 0. 1 A 0. 1 0. 2 A 0. 7 0. 8 T G 0. 8 G T A 0. 6 … C 0. 7 G C 0. 2 0. 1 A G T C 0. 25 p = 0. 18 p = 0. 255 = 0. 00098

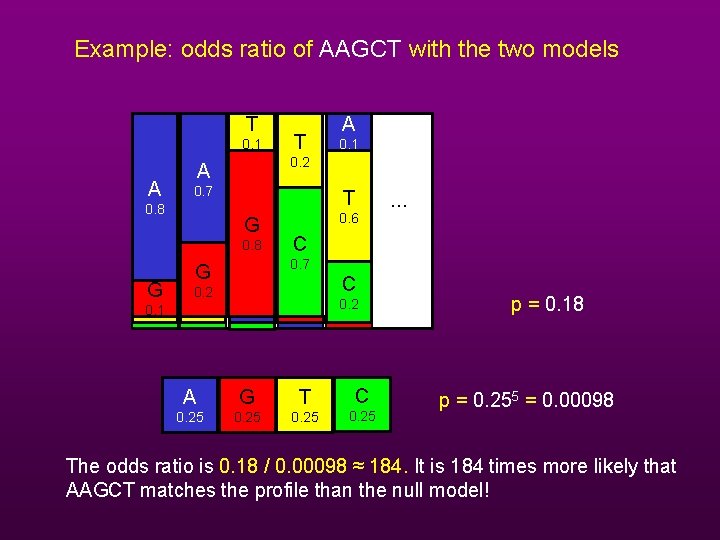
Example: odds ratio of AAGCT with the two models T 0. 1 A 0. 1 0. 2 A 0. 7 0. 8 T G 0. 8 G T A 0. 6 … C 0. 7 G C 0. 2 0. 1 A G T C 0. 25 p = 0. 18 p = 0. 255 = 0. 00098 The odds ratio is 0. 18 / 0. 00098 ≈ 184. It is 184 times more likely that AAGCT matches the profile than the null model!

Like with substitution scoring matrices, we prefer the log-odds as a profile score A positive log-odds (score) indicates a match.

Digression: interpreting BLAST results The bit score is a scaled log-odds of homology versus chance

Digression: interpreting BLAST results E value is the expected number of hits with scores at least S

A better way to model motifs REGULAR EXPRESSIONS “(TTR[ATC]WT) N{15, 22} (TRWWAT)” Can find alternative members of a class Treat alternative character states as equally likely. Treat all spacer lengths as equally likely. PROFILES (Position-Specific Score Matrices) Turn a multiple sequence alignment into a multidimensional (by position) multinomial distribution. Explicit accounting of observed character states Cannot handle gaps (separate models must be made for different spacer length -- O’Neill and Chiafari 1989) Can't be used to make alignments

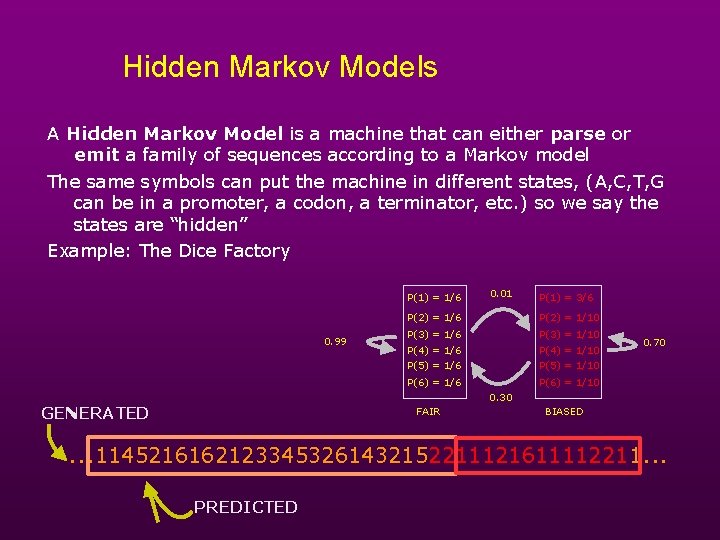
Hidden Markov Models A Hidden Markov Model is a machine that can either parse or emit a family of sequences according to a Markov model The same symbols can put the machine in different states, (A, C, T, G can be in a promoter, a codon, a terminator, etc. ) so we say the states are “hidden” Example: The Dice Factory P(1) = 1/6 0. 99 0. 01 P(1) = 3/6 P(2) = 1/10 P(3) = 1/6 P(3) = 1/10 P(4) = 1/6 P(5) = 1/6 P(4) = 1/10 P(5) = 1/10 P(6) = 1/6 P(6) = 1/10 0. 70 0. 30 GENERATED FAIR BIASED . . . 11452161621233453261432152211121611112211. . . PREDICTED

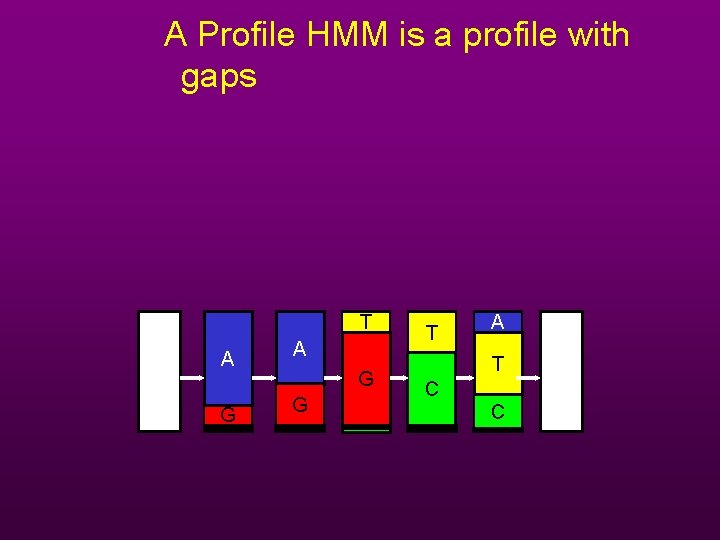
A Profile HMM is a profile with gaps T A G G T A T C C

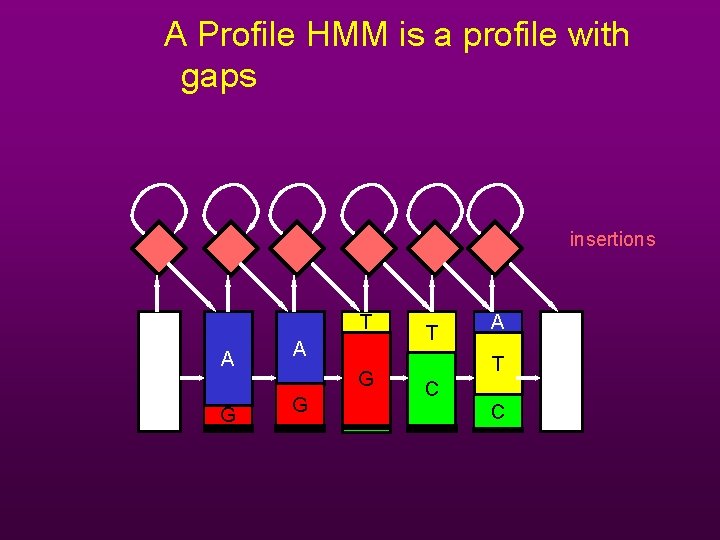
A Profile HMM is a profile with gaps insertions T A G G T A T C C

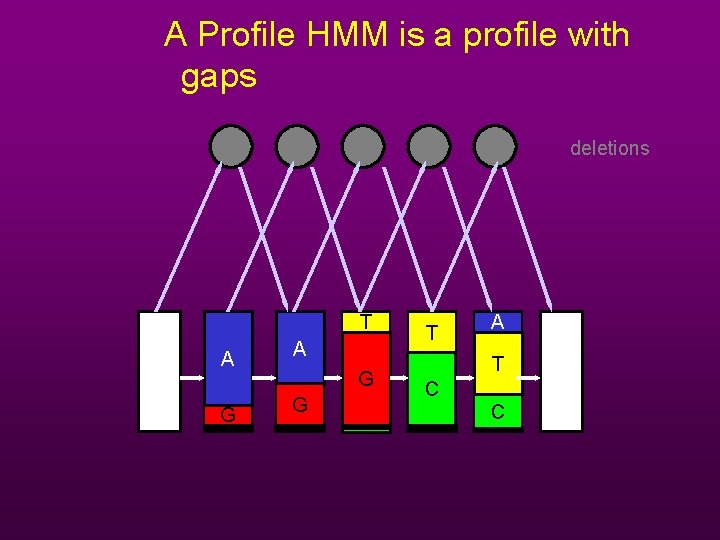
A Profile HMM is a profile with gaps deletions T A G G T A T C C

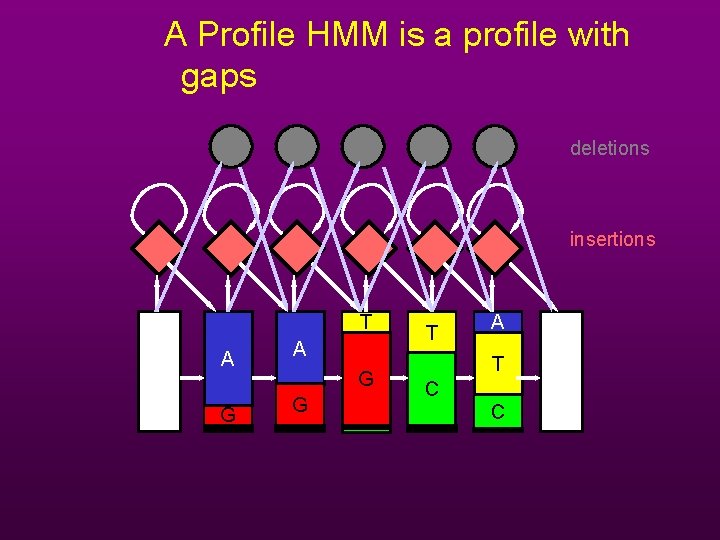
A Profile HMM is a profile with gaps deletions insertions T A G G T A T C C

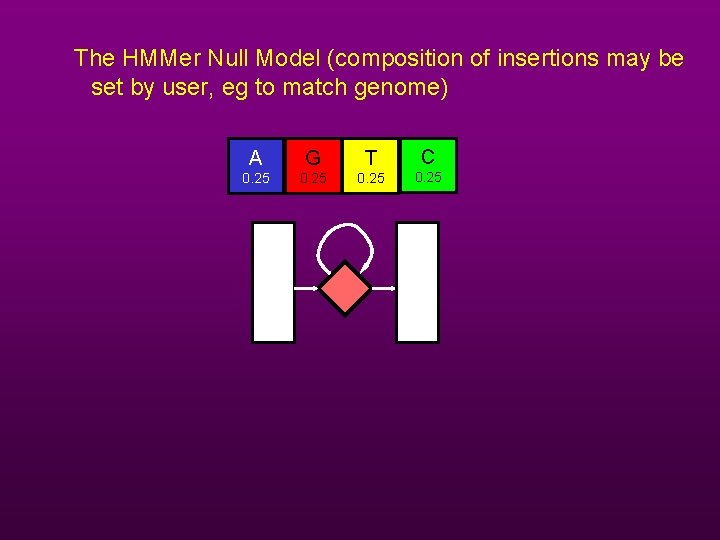
The HMMer Null Model (composition of insertions may be set by user, eg to match genome) A G T C 0. 25

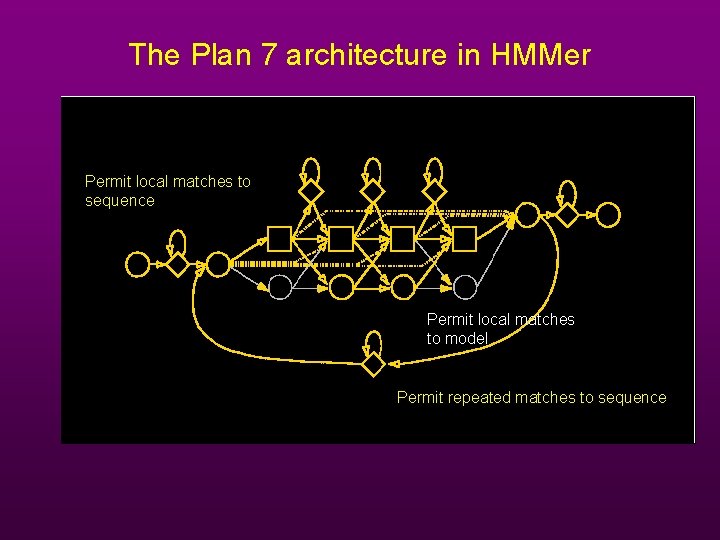
The Plan 7 architecture in HMMer Permit local matches to sequence Permit local matches to model Permit repeated matches to sequence

HMMer 2 (pronounced 'hammer', as in, “Why BLAST if you can hammer? ”)

The HMMer 2 design separates models from algorithms With the same alignment or model design, you can easily change the search algorithm (encoded in the HMM) to do: Multihit Global alignments of model to sequence Multihit Smith-Waterman (local with respect to both model and sequence, multiple non-overlapping hits to sequence allowed) Single (best) hit variants of both of the above.

This separation of model from algorithm provides a ready framework for sequence analysis (programs provided in HMMer) hmmalign Align sequences to an existing model. hmmbuild Build a model from a multiple sequence alignment. hmmcalibrate Takes an HMM and empirically determines parameters that are used to make searches more sensitive, by calculating more accurate expectation value scores (E -values). hmmconvert Convert a model file into different formats, including a compact HMMER 2 binary format, and “best effort” emulation of GCG profiles. hmmemit Emit sequences probabilistically from a profile HMM. hmmfetch Get a single model from an HMM database. hmmindex Index an HMM database. hmmpfam Search an HMM database for matches to a query sequence. hmmsearch Search a sequence database for matches to an HMM.

HMMer 2 format can be automatically converted for use with SAM