Introduction to Probabilistic Models for Computational Biology Lectures

Introduction to Probabilistic Models for Computational Biology Lectures 2 – Oct 3, 2011 CSE 527 Computational Biology, Fall 2011 Instructor: Su-In Lee TA: Christopher Miles Monday & Wednesday 12: 00 -1: 20 Johnson Hall (JHN) 022 1

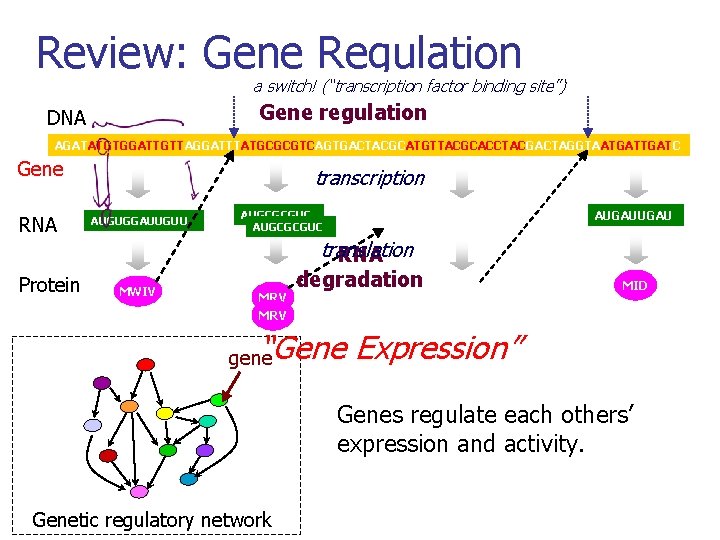
Review: Gene Regulation a switch! (“transcription factor binding site”) Gene regulation DNA AGATATGTGGATTGTTAGGATTTATGCGCGTCAGTGACTACGCATGTTACGCACCTACGACTAGGTAATGATTGATC Gene RNA Protein transcription AUGUGGAUUGUU MWIV AUGCGCGUC MRV AUGUUACGCACCUAC translation RNA degradation MLRTY AUGAUUAU MID “Gene Expression” gene Genes regulate each others’ expression and activity. Genetic regulatory network

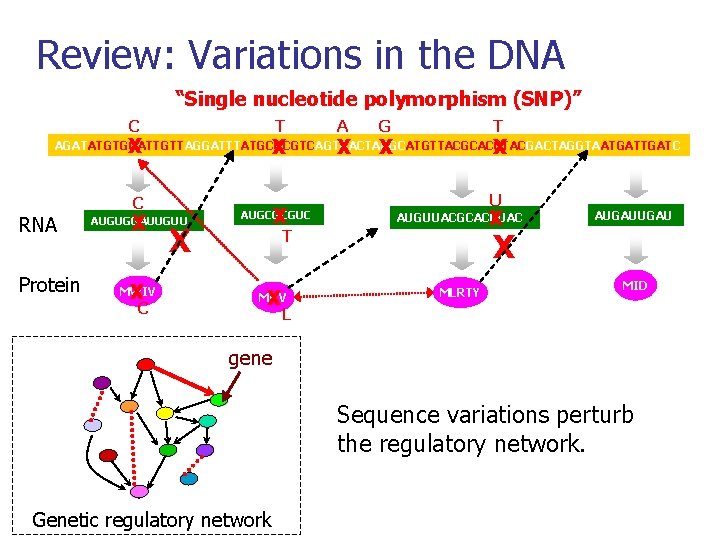
Review: Variations in the DNA “Single nucleotide polymorphism (SNP)” C T X X A X T G X X AGATATGTGGATTGTTAGGATTTATGCGCGTCAGTGACTACGCATGTTACGCACCTACGACTAGGTAATGATC RNA Protein C X AUGUGGAUUGUU X MWIV C X X AUGCGCGUC U X AUGUUACGCACCUAC T X MRV AUGAU X MLRTY MID L gene Sequence variations perturb the regulatory network. Genetic regulatory network

Outline n Probabilistic models in biology n Model selection problems n Mathematical foundations n Bayesian networks n n Probabilistic Graphical Models: Principles and Techniques, Koller & Friedman, The MIT Press Learning from data n n Maximum likelihood estimation Expectation and maximization 4

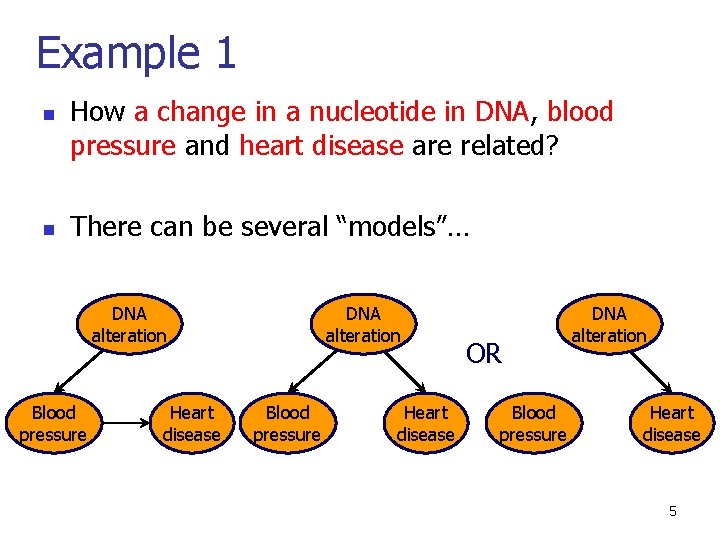
Example 1 n n How a change in a nucleotide in DNA, blood pressure and heart disease are related? There can be several “models”… DNA alteration Blood pressure Heart disease OR Blood pressure DNA alteration Heart disease 5

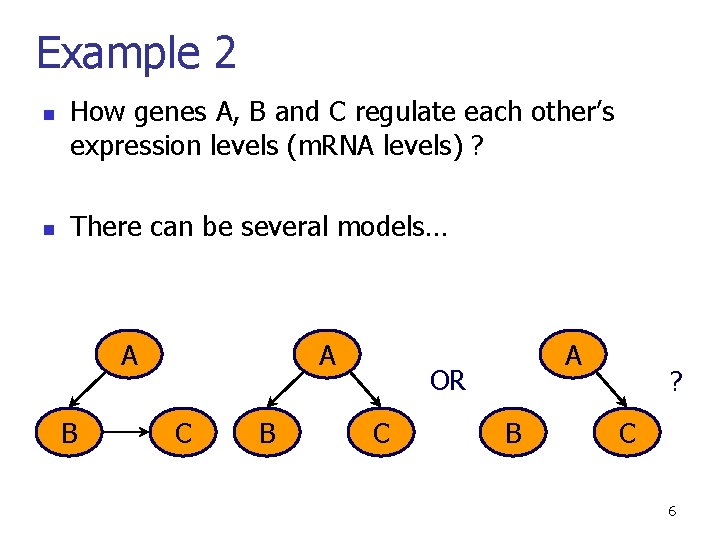
Example 2 n n How genes A, B and C regulate each other’s expression levels (m. RNA levels) ? There can be several models… A B A C B A OR C B ? C 6

Model III A A A B C B Exp 1 Exp 2 OR C … Gene A n n C Exp N N instances Gene B Probabilistic graphical models n n B ? Gene C A graphical representation of statistical dependencies. Statistical dependencies between expression levels of genes A, B, C? Probability that model x is true given the data n Model selection: argmaxx P(model x is true | Data) 7

Outline n Probabilistic models in biology n Model selection problem n Mathematical foundations n Bayesian networks n Learning from data n n Maximum likelihood estimation Expectation and maximization 8

Probability Theory Review n Assume random variables Val(A)={a 1, a 2, a 3}, Val(B)={b 1, b 2} n Conditional probability n Definition n Chain rule n Bayes’ rule n Probabilistic independence 9

Probabilistic Representation n Joint distribution P over {x 1, …, xn} n n n xi is binary 2 n-1 entries If x’s are independent n P(x) = p(x 1) … p(xn) 10

Conditional Parameterization n The Diabetes example n n n Genetic risk (G), Diabetes (D) Val (G) = {g 1, g 0}, Val (D) = {d 1, d 0} P(G, D) = P(G) P(D|G) n n P(G): Prior distribution P(D|G): Conditional probabilistic distribution (CPD) Genetic risk Diabetes 11

Naïve Bayes Model - Example n Elaborating the diabetes example, n n Genetic Risk (G), Diabetes (D), Hypertension (H) Val (G) = {g 1, g 0}, Val (D) = {d 1, d 0}, Val (H) = {h 1, h 0} 8 entries If S and G are independent given I, n n P(G, D, H) = P(G)P(D|G)P(H|G) 5 entries; more compact than joint Genetic risk Diabetes Hypertension 12

Naïve Bayes Model n A class C where Val (C) = {c 1, …, ck}. n Finding variables x 1, …, xn n Naïve Bayes assumption n The findings are conditionally independent given the individual’s class. The model factorizes as: The Diabetes example n class: Genetic risk, findings: Diabetes, Hypertension 13

Naïve Bayes Model - Example n Medical diagnosis system n n Class C: disease Findings X: symptoms n Computing the confidence: n Drawbacks n Strong assumptions 14

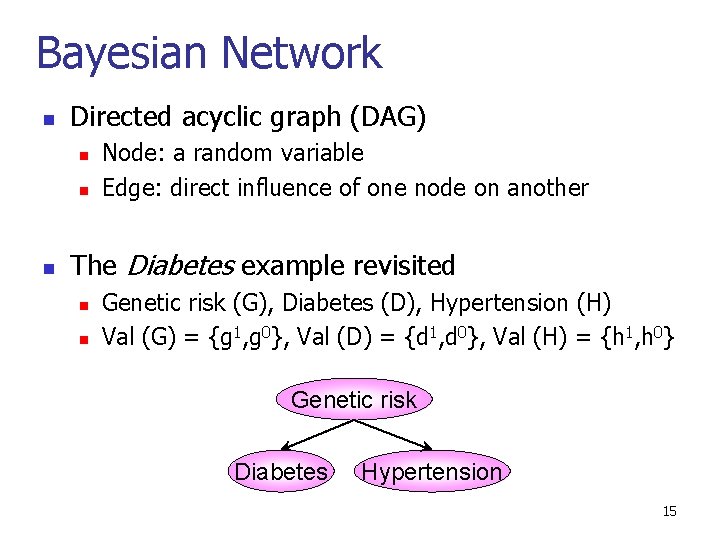
Bayesian Network n Directed acyclic graph (DAG) n n n Node: a random variable Edge: direct influence of one node on another The Diabetes example revisited n n Genetic risk (G), Diabetes (D), Hypertension (H) Val (G) = {g 1, g 0}, Val (D) = {d 1, d 0}, Val (H) = {h 1, h 0} Genetic risk Diabetes Hypertension 15

Bayesian Network Semantics n A Bayesian network structure G is a directed acyclic graph whose nodes represent random variables X 1, …, Xn. n n n Pa. Xi: parents of Xi in G Non. Descendants. Xi: variables in G that are not descendants of Xi. G encodes the following set of conditional independence assumptions, called the local Markov assumptions, and denoted by IL(G): x 2 For each variable Xi: x 1 x 3 x 4 x 11 x 3 x 10 x 7 x 5 x 6 x 8 x 9 16

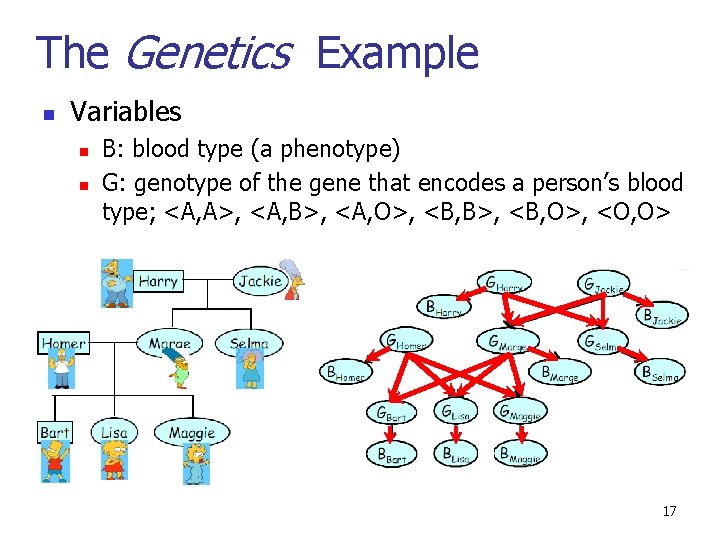
The Genetics Example n Variables n n B: blood type (a phenotype) G: genotype of the gene that encodes a person’s blood type; <A, A>, <A, B>, <A, O>, <B, B>, <B, O>, <O, O> 17

Bayesian Network Joint Distribution n n Let G be a Bayesian network graph over the variables X 1, …, Xn. We say that a distribution P factorizes according to G if P can be expressed as: A Bayesian network is a pair (G, P) where P factorizes over G, and where P is specified as a set of CPDs associated with G’s nodes. 18

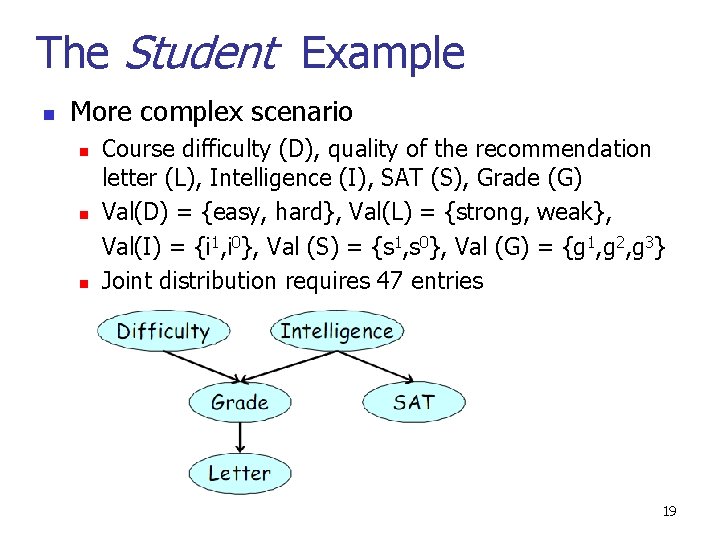
The Student Example n More complex scenario n n n Course difficulty (D), quality of the recommendation letter (L), Intelligence (I), SAT (S), Grade (G) Val(D) = {easy, hard}, Val(L) = {strong, weak}, Val(I) = {i 1, i 0}, Val (S) = {s 1, s 0}, Val (G) = {g 1, g 2, g 3} Joint distribution requires 47 entries 19

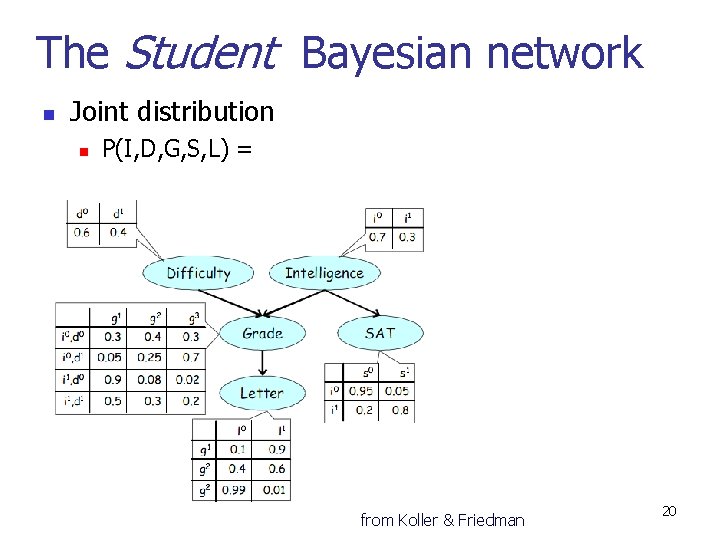
The Student Bayesian network n Joint distribution n P(I, D, G, S, L) = from Koller & Friedman 20

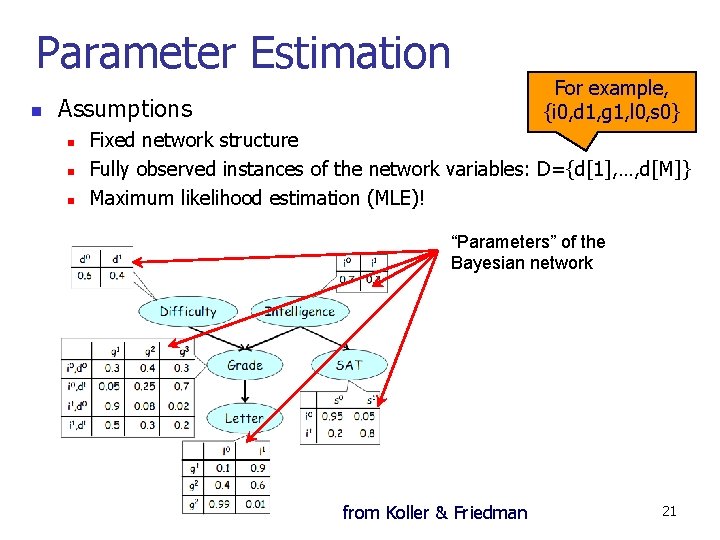
Parameter Estimation n Assumptions n n n For example, {i 0, d 1, g 1, l 0, s 0} Fixed network structure Fully observed instances of the network variables: D={d[1], …, d[M]} Maximum likelihood estimation (MLE)! “Parameters” of the Bayesian network from Koller & Friedman 21

Outline n Probabilistic models in biology n Model selection problem n Mathematical foundations n Bayesian networks n Learning from data n n Maximum likelihood estimation Expectation and maximization 22

Acknowledgement n Profs Daphne Koller & Nir Friedman, “Probabilistic Graphical Models” 23