Introduction to Powder XRay Diffraction History Basic Principles

Introduction to Powder X-Ray Diffraction History Basic Principles Introduction-to-XRD. 1 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

History: Wilhelm Conrad Röntgen discovered 1895 the X-rays. 1901 he was honoured by the Noble prize for physics. In 1995 the German Post edited a stamp, dedicated to W. C. Röntgen. Introduction-to-XRD. 2 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

The Principles of an X-ray Tube X-Ray Cathode Fast electrons Anode focus Introduction-to-XRD. 3 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

The Principle of Generation Bremsstrahlung Ejected electron (slowed down and changed direction) nucleus Fast incident electrons Atom of the anodematerial X-ray Introduction-to-XRD. 4 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

The Principle of Generation the Characteristic Radiation Photoelectron M Emission K -Quant L K Electron L -Quant K -Quant Introduction-to-XRD. 5 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

The Generating of X-rays Bohr`s model Introduction-to-XRD. 6 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

The Generating of X-rays energy levels (schematic) of the electrons M Intensity ratios K K K L K K K Introduction-to-XRD. 7 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved
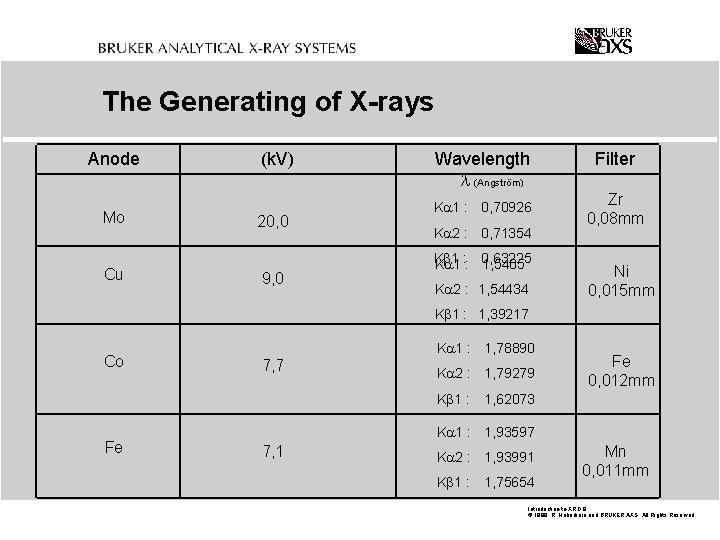
The Generating of X-rays Anode Mo Cu (k. V) 20, 0 9, 0 Wavelength Angström K 1 : 0, 70926 K 2 : 0, 71354 K 1 : : 0, 63225 1, 5405 K 2 : 1, 54434 Filter Zr 0, 08 mm Ni 0, 015 mm K 1 : 1, 39217 Co K 1 : 1, 78890 7, 7 K 2 : 1, 79279 K 1 : Fe Fe 0, 012 mm 1, 62073 K 1 : 1, 93597 7, 1 K 2 : 1, 93991 K 1 : 1, 75654 Mn 0, 011 mm Introduction-to-XRD. 8 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved
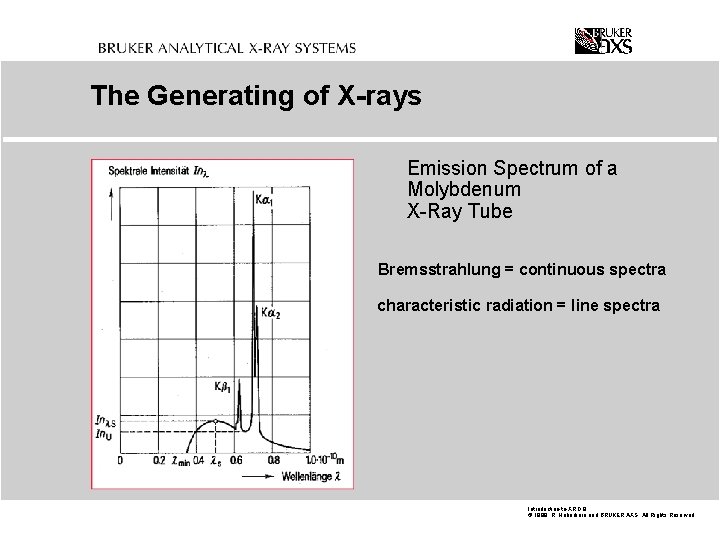
The Generating of X-rays Emission Spectrum of a Molybdenum X-Ray Tube Bremsstrahlung = continuous spectra characteristic radiation = line spectra Introduction-to-XRD. 9 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved
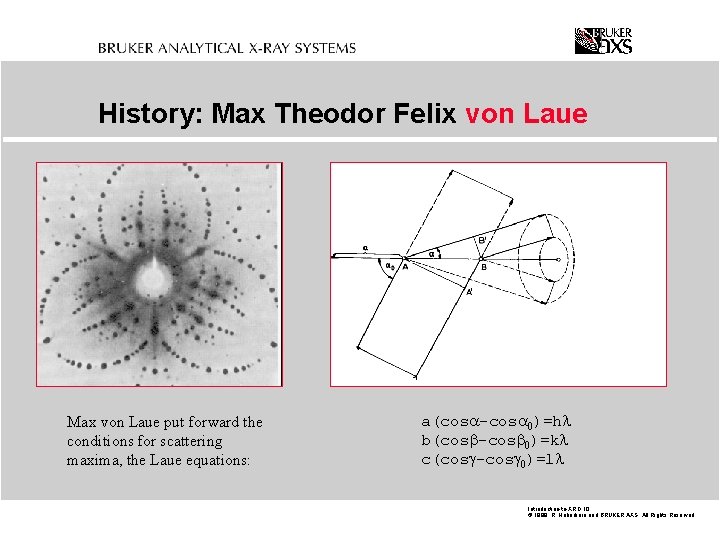
History: Max Theodor Felix von Laue Max von Laue put forward the conditions for scattering maxima, the Laue equations: a(cos -cos )=h b(cos -cos )=k c(cosg-cosg )=l Introduction-to-XRD. 10 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

Laue’s Experiment in 1912 Single Crystal X-ray Diffraction Tube Crystal Collimator Film Introduction-to-XRD. 11 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

Powder X-ray Diffraction Film Tube Powder Introduction-to-XRD. 12 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

Powder Diffraction Pattern Introduction-to-XRD. 13 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved
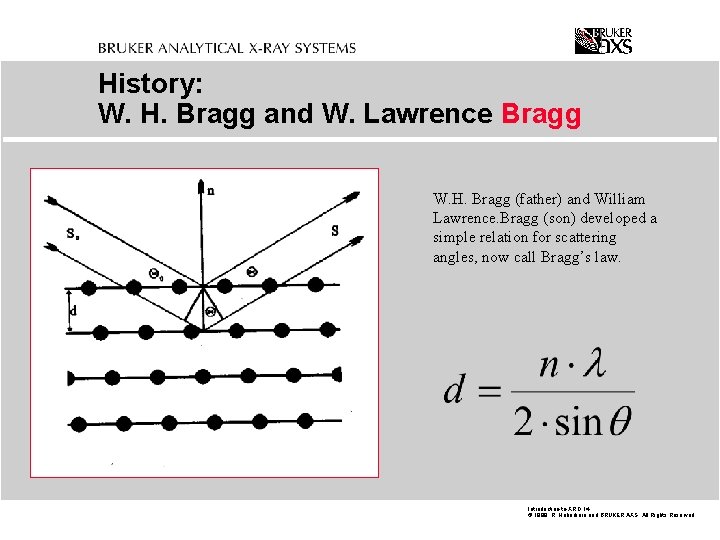
History: W. H. Bragg and W. Lawrence Bragg W. H. Bragg (father) and William Lawrence. Bragg (son) developed a simple relation for scattering angles, now call Bragg’s law. Introduction-to-XRD. 14 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

Another View of Bragg´s Law n = 2 d sin Introduction-to-XRD. 15 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

Crystal Systems Introduction-to-XRD. 16 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

Reflection Planes in a Cubic Lattice Introduction-to-XRD. 17 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved
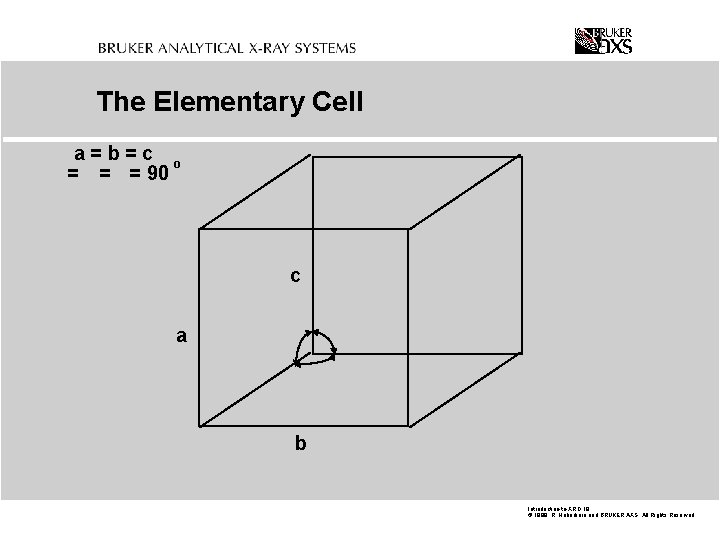
The Elementary Cell a=b=c o = = = 90 c a b Introduction-to-XRD. 18 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

Relationship between d-value and the Lattice Constants Bragg´s law n The wavelength is known n Theta is the half value of the peak position n d will be calculated Equation for the determination of the d-value of a tetragonal elementary cell n h, k and l are the Miller indices of the peaks n a and c are lattice parameter of the elementary cell n if a and c are known it is possible to calculate the peak position n if the peak position is known it is possible to calculate the lattice parameter Introduction-to-XRD. 19 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved
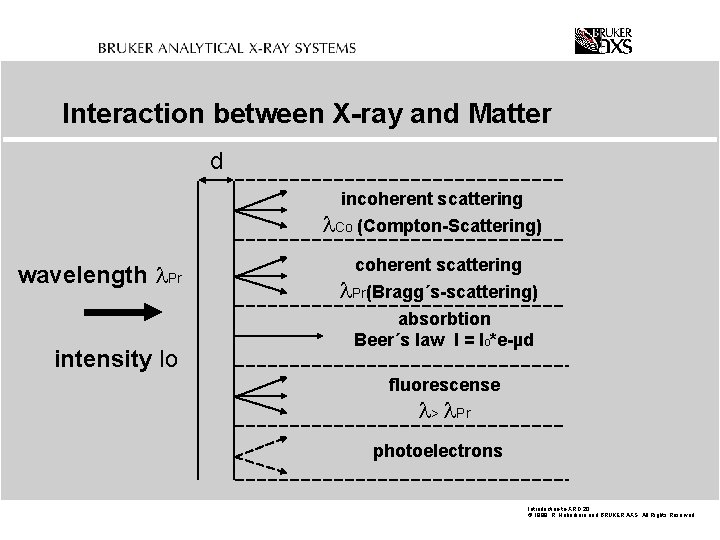
Interaction between X-ray and Matter d incoherent scattering Co (Compton-Scattering) wavelength Pr intensity Io coherent scattering Pr(Bragg´s-scattering) absorbtion Beer´s law I = I 0*e-µd fluorescense > Pr photoelectrons Introduction-to-XRD. 20 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

History (4): C. Gordon Darwin, grandson of C. Robert Darwin (picture) developed 1912 dynamic theory of scattering of Xrays at crystal lattice Introduction-to-XRD. 21 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

History (5): P. P. Ewald 1916 published a simple and more elegant theory of X-ray diffraction by introducing the reciprocal lattice concept. Compare Bragg’s law (left), modified Bragg’s law (middle) and Ewald’s law (right). Introduction-to-XRD. 22 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved
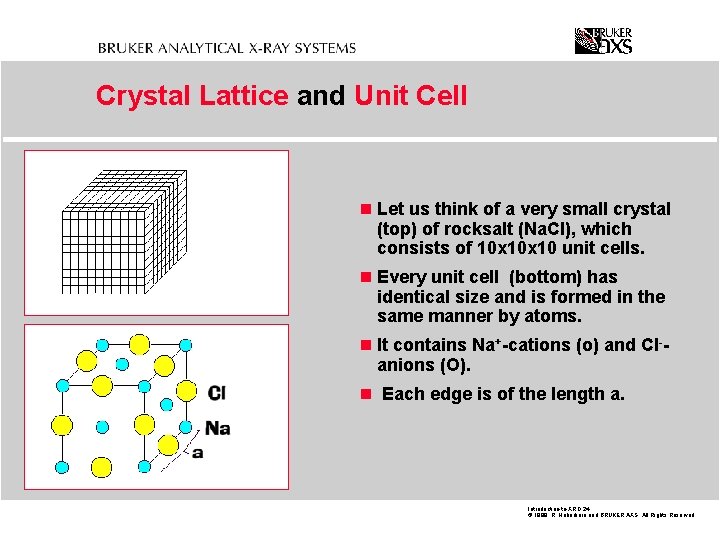
Crystal Lattice and Unit Cell n Let us think of a very small crystal (top) of rocksalt (Na. Cl), which consists of 10 x 10 unit cells. n Every unit cell (bottom) has identical size and is formed in the same manner by atoms. n It contains Na+-cations (o) and Cl-- anions (O). n Each edge is of the length a. Introduction-to-XRD. 24 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

Bragg’s Description n The incident beam will be scattered at all scattering centres, which lay on lattice planes. n The beam scattered at different lattice planes must be scattered coherent, to give an maximum in intensity. n The angle between incident beam and the lattice planes is called q. n The angle between incident and scattered beam is 2 q. n The angle 2 q of maximum intensity is called the Bragg angle. Introduction-to-XRD. 25 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

Bragg’s Law n A powder sample results in cones with high intensity of scattered beam. n Above conditions result in the Bragg equation n or Introduction-to-XRD. 26 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

Film Chamber after Straumannis n The powder is fitted to a glass fibre or into a glass capillary. n X-Ray film, mounted like a ring around the sample, is used as detector. n Collimators shield the film from radiation scattered by air. Introduction-to-XRD. 27 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

Film Negative and Straumannis Chamber Remember n The beam scattered at different lattice planes must be scattered coherent, to give an maximum of intensity. n Maximum intensity for a specific (hkl)-plane with the spacing d between neighbouring planes at the Bragg angle 2 q between primary beam and scattered radiation. n This relation is quantified by Bragg’s law. n A powder sample gives cones with high intensity of scattered beam. Introduction-to-XRD. 28 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

D 8 ADVANCE Bragg-Brentano Diffractometer n A scintillation counter may be used as detector instead of film to yield exact intensity data. n Using automated goniometers step by step scattered intensity may be measured and stored digitally. n The digitised intensity may be very detailed discussed by programs. n More powerful methods may be used to determine lots of information about the specimen. Introduction-to-XRD. 29 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved
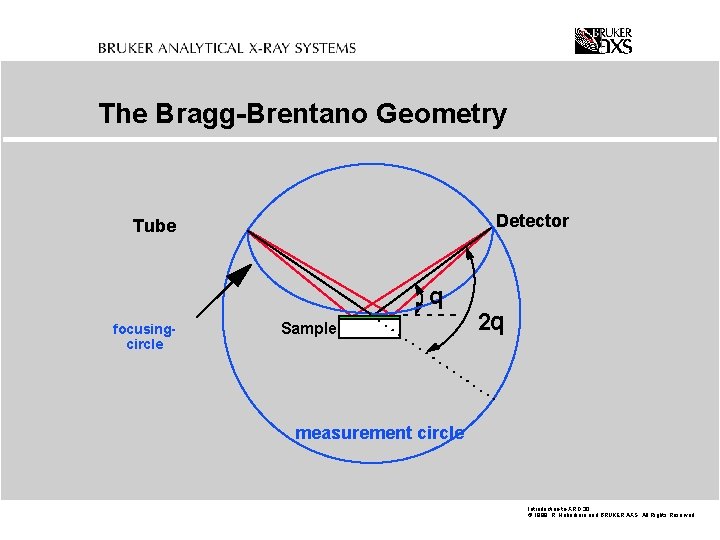
The Bragg-Brentano Geometry Detector Tube q focusingcircle Sample 2 q measurement circle Introduction-to-XRD. 30 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved
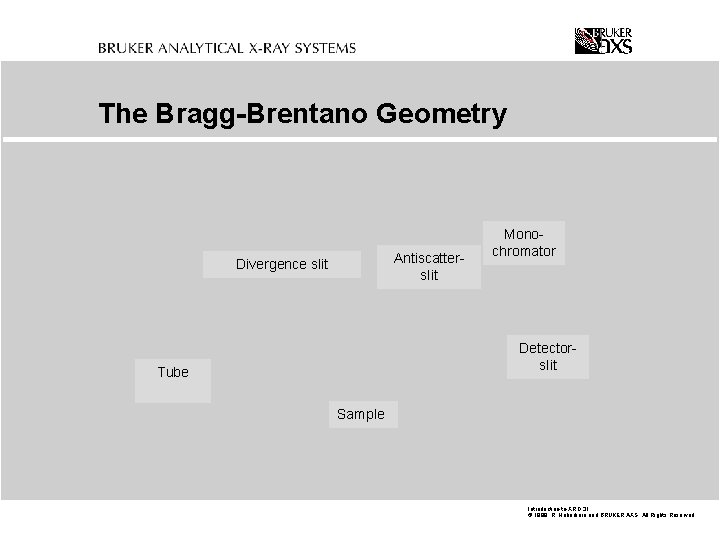
The Bragg-Brentano Geometry Antiscatterslit Divergence slit Monochromator Detectorslit Tube Sample Introduction-to-XRD. 31 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved
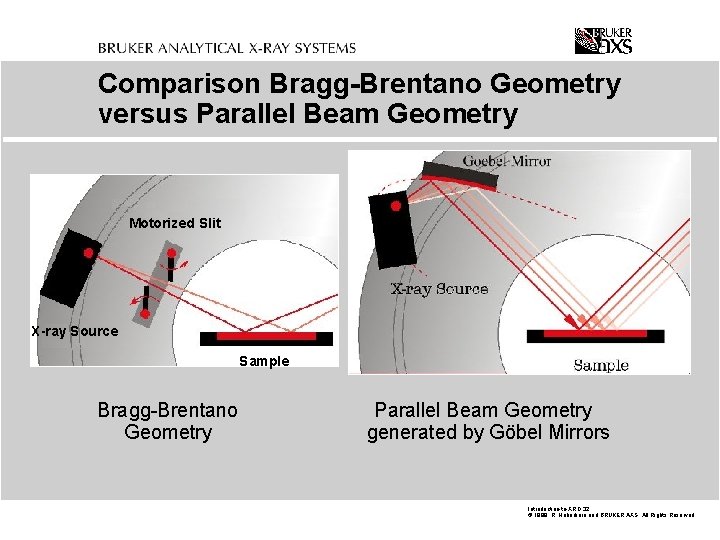
Comparison Bragg-Brentano Geometry versus Parallel Beam Geometry Motorized Slit X-ray Source Sample Bragg-Brentano Geometry Parallel Beam Geometry generated by Göbel Mirrors Introduction-to-XRD. 32 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved
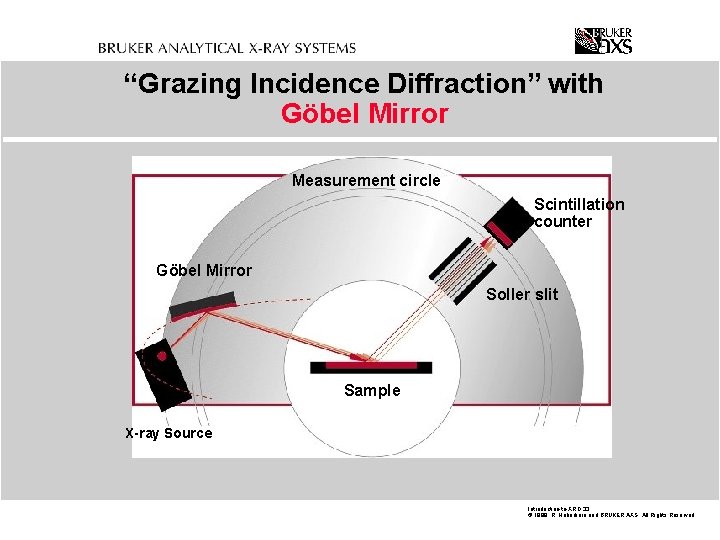
“Grazing Incidence Diffraction” with Göbel Mirror Measurement circle Scintillation counter Göbel Mirror Soller slit Sample X-ray Source Introduction-to-XRD. 33 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

What is a Powder Diffraction Pattern? a powder diffractogram is the result of a convolution of a) the diffraction capability of the sample (Fhkl) and b) a complex system function. The observed intensity yoi at the data point i is the result of yoi = of intensity of "neighbouring" Bragg peaks + background The calculated intensity yci at the data point i is the result of yci = structure model + sample model + diffractometer model + background model Introduction-to-XRD. 34 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

Which Information does a Powder Pattern offer? n peak position dimension of the elementary cell n peak intensity content of the elementary cell n peak broadening strain/crystallite size n scaling factor quantitative phase amount n diffuse background false order n modulated background close order Introduction-to-XRD. 35 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved
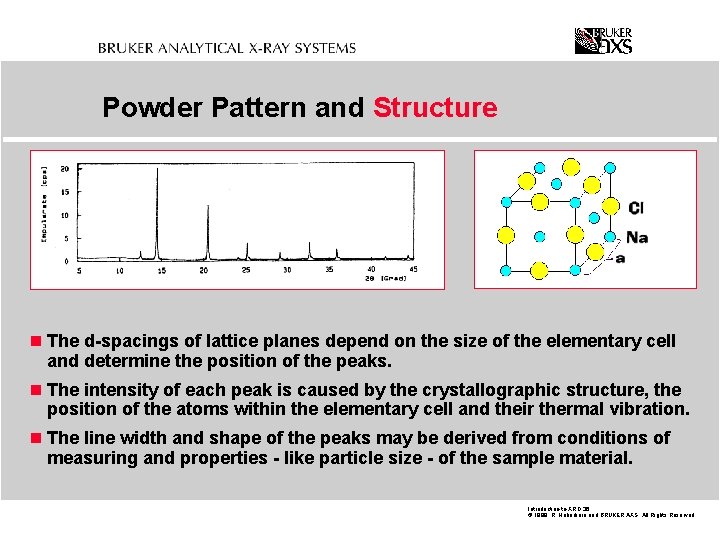
Powder Pattern and Structure n The d-spacings of lattice planes depend on the size of the elementary cell and determine the position of the peaks. n The intensity of each peak is caused by the crystallographic structure, the position of the atoms within the elementary cell and their thermal vibration. n The line width and shape of the peaks may be derived from conditions of measuring and properties - like particle size - of the sample material. Introduction-to-XRD. 36 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

Principles of the Rietveld method n Hugo M. Rietveld, 1967/1969 n The Rietveld method allows the optimization of a certain amount of model parameters (structure & instrument), to get a best fit between a measured and a calculated powder diagram. n The parameter will be varied with a non linear least- squares algorythm, that the difference will be minimized between the measured and the calculated Pattern: Introduction-to-XRD. 37 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

Basis formula of the Rietveldmethod n SF : Scaling factor n Mk : Multiplicity of the reflections k n Pk : Value of a preffered orientation function for the reflections k n Fk 2 : Structure factor of the reflections k n LP : Value of the Lorentz-Polarisations function for the reflections k n Fk : Peak profile function for the reflections k on the position i n ybi : Value of the background at the position i n k : Index over all reflexes with intensity on the position i Introduction-to-XRD. 38 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

Comparison of Profile Shape and Intensity Accuracy between Parallel Beam Göbel Mirror and Bragg-Brentano Parafocusing Diffractometers A. Seyfarth, A. Kern & G. Menges AXS Gmb. H, Östliche Rheinbrückenstr. 50, D-76187 Karlsruhe Fifth European Powder Diffraction Conference, EPDIC-5, Abstracts, p. 227 (1997) XVII Conference on Applied Crystallography, CAC 17, Abstracts, p. 45 (1997) Introduction-to-XRD. 39 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

Göbel Mirrors for parallel Beam n Graded and bent multilayers optics n Capture a large solid angle of X-rays emitted by the source n Produce an intense and parallel beam virtually free of Cu Kß radiation Introduction-to-XRD. 40 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved
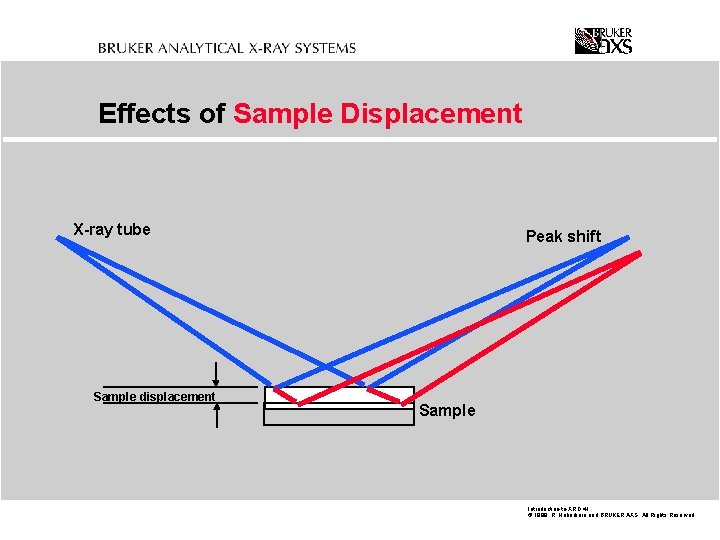
Effects of Sample Displacement X-ray tube Sample displacement Peak shift Sample Introduction-to-XRD. 41 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved
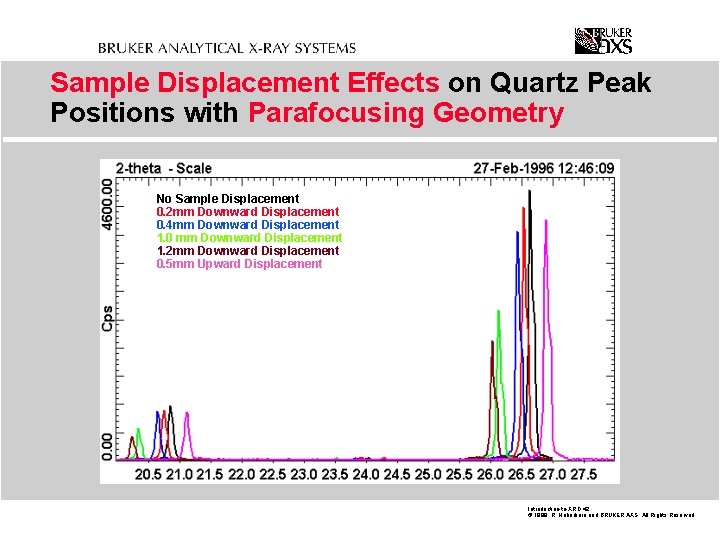
Sample Displacement Effects on Quartz Peak Positions with Parafocusing Geometry No Sample Displacement 0. 2 mm Downward Displacement 0. 4 mm Downward Displacement 1. 0 mm Downward Displacement 1. 2 mm Downward Displacement 0. 5 mm Upward Displacement Introduction-to-XRD. 42 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved
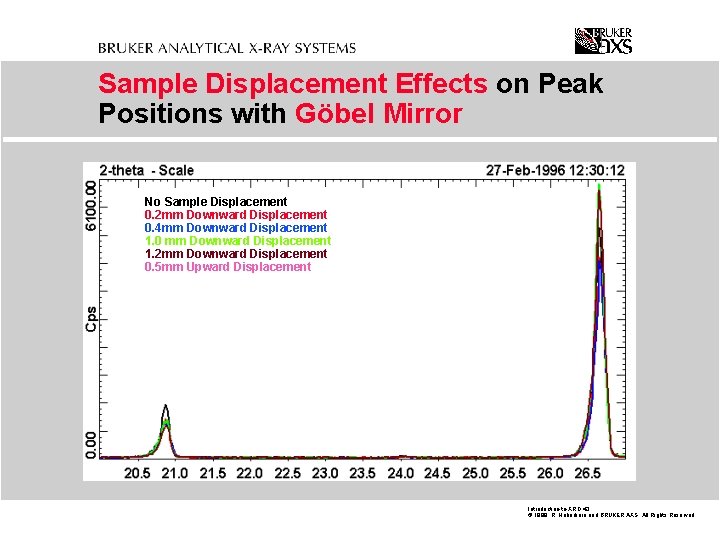
Sample Displacement Effects on Peak Positions with Göbel Mirror No Sample Displacement 0. 2 mm Downward Displacement 0. 4 mm Downward Displacement 1. 0 mm Downward Displacement 1. 2 mm Downward Displacement 0. 5 mm Upward Displacement Introduction-to-XRD. 43 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved
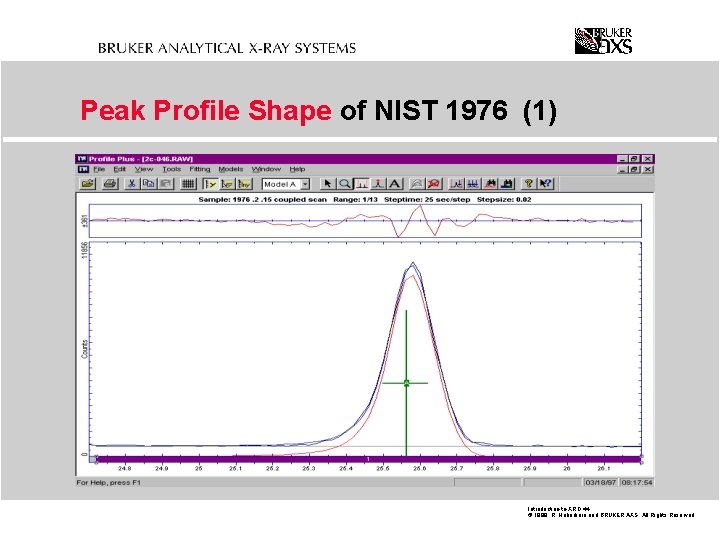
Peak Profile Shape of NIST 1976 (1) Introduction-to-XRD. 44 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved
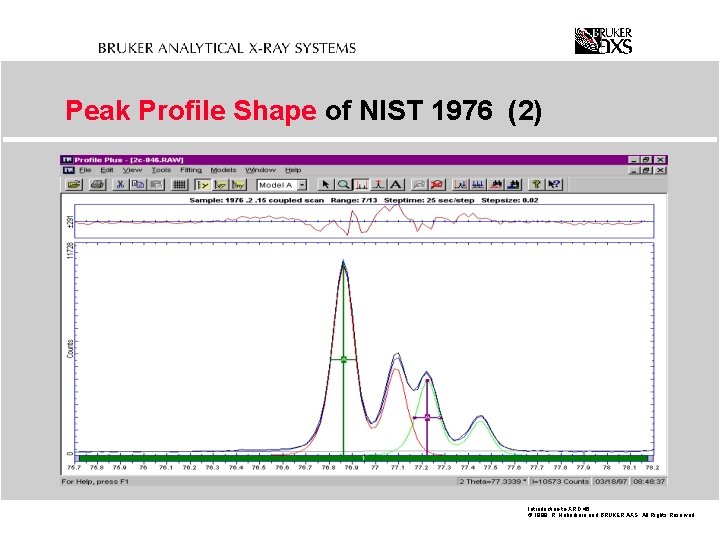
Peak Profile Shape of NIST 1976 (2) Introduction-to-XRD. 45 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved
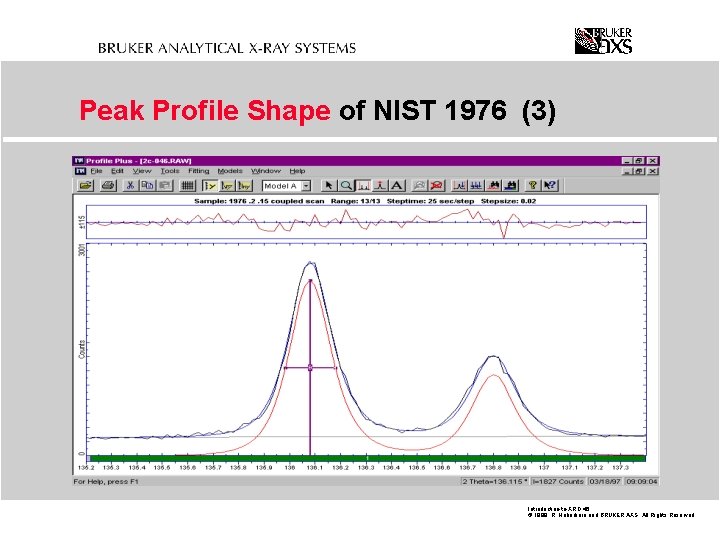
Peak Profile Shape of NIST 1976 (3) Introduction-to-XRD. 46 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

Instrument Response Function D 5005 Theta/2 Theta Göbel Mirror, 0. 2 mm divergence slit, 2° vertical Soller slit and 0. 15° collimator. Introduction-to-XRD. 47 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

Peak Shape Asymmetry D 5005 Theta/2 Theta Göbel Mirror, 0, 2 mm divergence slit, 2° vertical Soller slit and 0. 15° collimator. Introduction-to-XRD. 48 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved

Instrument Resolution Functions Introduction-to-XRD. 49 © 1999 R. Haberkorn and BRUKER AXS All Rights Reserved
- Slides: 48