Introduction to Optoelectronics Optical communication 2 Prof Katsuaki

Introduction to Optoelectronics Optical communication (2) Prof. Katsuaki Sato

Lasers • Spontaneous emission and stimulated emission • Application of Lasers • Classification of lasers according to the way of pumping • Laser diodes – What is semiconductor? – p/n junction diode – Light emitting diode and laser diode

What is Laser? • Spontaneous and stimulated emission • Different pumping methods • Characteristics of laser light

Spontaneous and stimulated emission • Spontaneous emission：Light emission by relaxation from the excited state to the ground state • stimulated emission：Light emission due to optical transition forced by optical stimulation; • This phenomenon is the laser=light amplification by stimulated emission of radiation

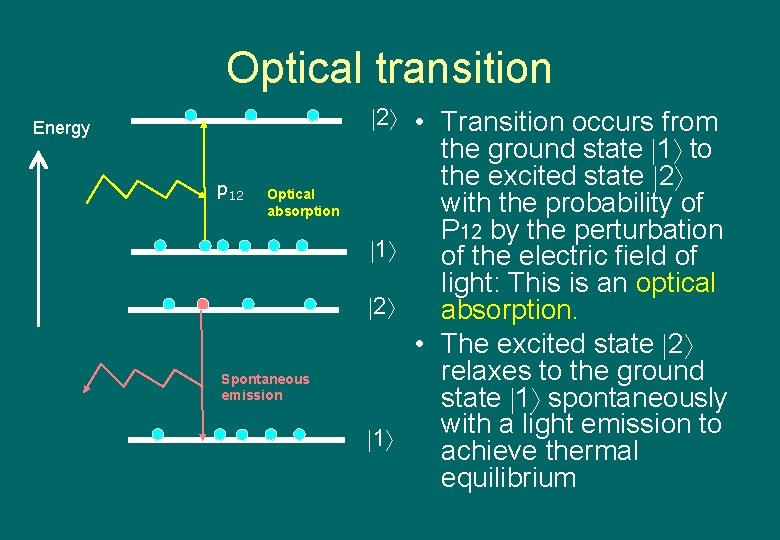
Optical transition 2 • Transition occurs from Energy p 12 Optical absorption Spontaneous emission the ground state 1 to the excited state 2 with the probability of P 12 by the perturbation 1 of the electric field of light: This is an optical 2 absorption. • The excited state 2 relaxes to the ground state 1 spontaneously with a light emission to 1 achieve thermal equilibrium

Energy Stimulated emission 2 • Transition from the E p 12 Stimulated emission p 21 excited state 2 to the ground state 1 occurs Stimulated emission by the stimulation of the electric field of incident 1 light with the transition probability of P 21(=P 12), leading to emission of a 2 photon. This process is called stimulated emission. • The number of photons is doubled since first 1 photon is not absorbed.

Emission is masked by absorption under normal condition N 2 Stimulated emission p 21 N 2 p 12 N 1 Optical absorption • Under normal condition 2 stimulated emission cannot be observed since absorption occurs at the same probability as 1 emission (P 12=P 21), and the population N 1 at 1 2 dominates N 2 at 2 due to Maxwell-Boltzmann distribution. Therefore, N 2 P 21<N 1 P 12 1

Maxwell-Boltzmann distribution Energy • The population at the excited state 2 located at E above the ground state 1 is expressed by a formula exp(- E/k. T) 2 exp(- E/k. T) E 1 0 1 Distribution function

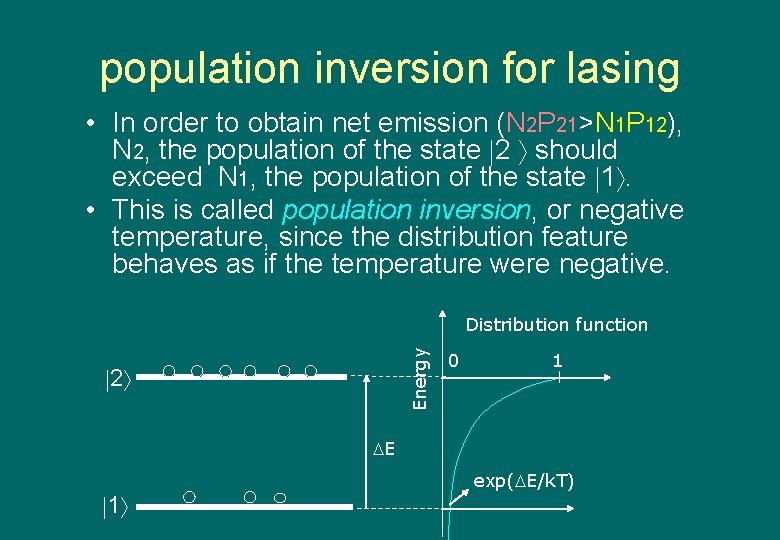
population inversion for lasing • In order to obtain net emission (N 2 P 21>N 1 P 12), N 2, the population of the state 2 should exceed N 1, the population of the state 1. • This is called population inversion, or negative temperature, since the distribution feature behaves as if the temperature were negative. Energy Distribution function 2 0 1 E 1 exp( E/k. T)

Characteristics of laser • Oscillator and amplifier of light wave • Wave-packets share the same phase leading to Coherence: two different lasers can make interference fringes Directivity: laser beam can go straight for a long distance Monochromaticity: laser wavelength is “pure” with narrow width High energy density: laser can heat a substance by focusing Ultra short pulse: laser pulse duration can be reduced as short as femtosecond (10 -15 s) • Bose condensation quantum state appearing macroscopically

Application of lasers • • • Optical Communications Optical Storages Laser Printers Diplays Laser Processing Medical Treatments

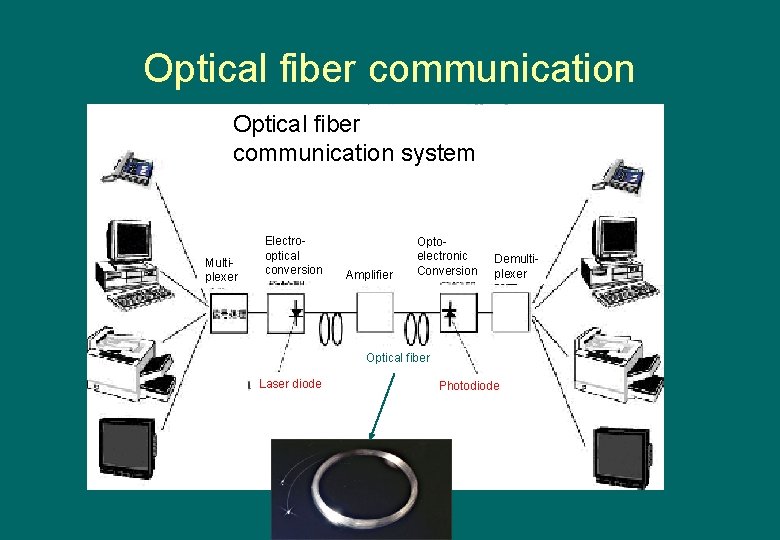
Optical fiber communication system Multiplexer Electrooptical conversion Amplifier Optoelectronic Conversion Demultiplexer Optical fiber Laser diode Photodiode

Optical Storages • CD、DVD、BD • MD、MO

Laser Printers photosensitive drum Computer BD lens controller optical fiber BD signal DC controller toric lens spherical lens polygon mirror horizontal sync mirror opt. box cylindrical lens laser diode/ laser driver http: //web. canon. jp/technology/detail/lbp/laser_unit/index. html video signal scanner motor/ motor driver

Laser Show • Polygon mirror

Laser Processing Web site of Fujitsu

Medical Treatment • CO 2 laser

Classification of lasers according to the way of pumping • Gas lasers： eg. , He-Ne, He-Cd, Ar+, CO 2, pump an excited state in the electronic structure of gas ions or molecules by discharge • Solid state lasers eg. , YAG: Nd, Al 2 O 3: Ti, Al 2 O 3: Cr(ruby)： pump an excited state of luminescenter (impurity atom) by optical excitation • Laser diodes (Semiconductor lasers) eg. , Ga. Al. As, In. Ga. N high density injection of electrons and holes to active layer of semiconductor through pn-junction

Gas laser He. Ne laser Showa Optronics Ltd. http: //www. soc-ltd. co. jp/index. html

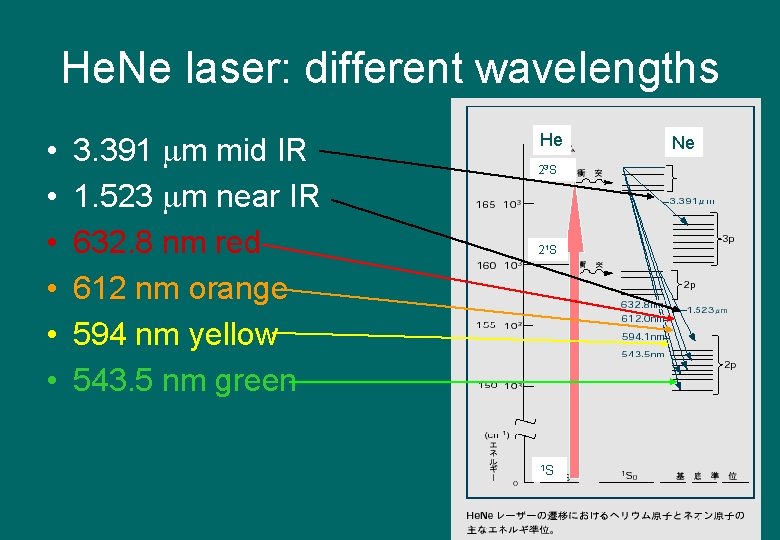
He. Ne laser, how it works • He atoms become excited by an impact excitation through collision • The ground state is 1 S (1 s 2; L=0, S=0) and the excited states are 1 S (1 s 1 2 s 1 ; L=0, S=0) and 3 S (1 s 1 2 s 1 ; L=0, S=1) • The energy is transferred to Ne atoms through collision. • Ne has ten electrons in the ground state 1 S 0 with 1 s 2 2 p 4 configuration, and possesses a lot of complex excited states http: //www. mgkk. com/products/pdf/02_4_He. Ne/024_213. pdf He 23 S 21 S 1 S Ne

He. Ne laser: different wavelengths • • • 3. 391 m mid IR 1. 523 m near IR 632. 8 nm red　赤 612 nm orange色 594 nm yellow黄色 543. 5 nm green グ リーン He 23 S 21 S 1 S Ne

Gas laser + Ar -ion • Blue 458 nm • Blue 488 nm • Blue-Green 514 nm laser

Application of gas laser Ar ion laser • Illumination (Laser show) • Photoluminescence Excitation Source

Gas laser CO 2 laser • 10. 6 m • Purpose – manufacturing – Medical surgery – Remote sensing

Solid state laser YAG laser YVO 4 laser • • YAG: Nd 1. 06 m Micro fabrication Pumping source for SHG http: //www. fesys. co. jp/sougou/sei hin/fa/laser/fal 3000. html

Solid state laser Titanium sapphire laser • Al 2 O 3: Ti 3+ (tunable） Ti-sapphire laser in Sato lab.

Solid state laser Ruby laser • • • Al 2 O 3: Cr 3+ Synthetic ruby single crystal Pumped by strong Xe lamp Emission wavelengths; 694. 3 nm Ethalon is used to select a wavelength of interest Ruby laser Ruby rod

LD (laser diode) • Laser diode is a semiconductor device which undergoes stimulated emission by recombination of injected carriers (electrons and holes), the concentration being far greater than that in thermal equilibrium.

What is semiconductor? • Semiconductors possess electrical conductivity between metals and insulators insulator diamond semiconductor metal Resistivity ( cm) Energy band gap (e. V) Conductivity (S/cm)

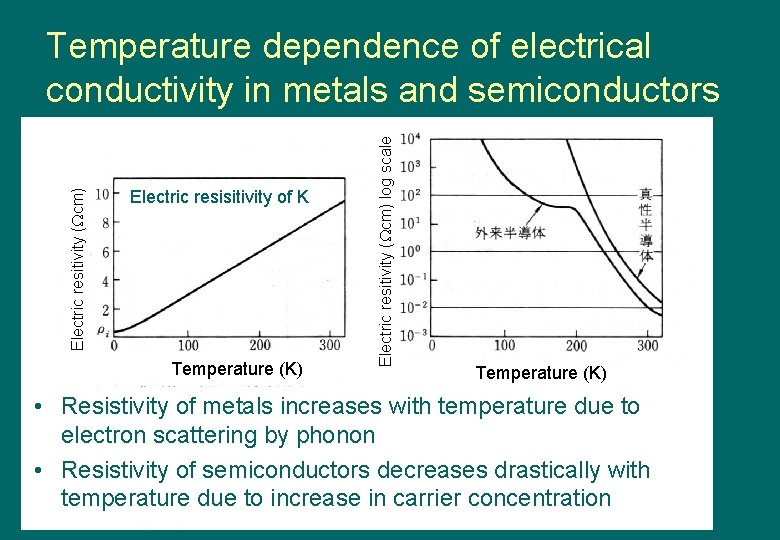
Electric resisitivity of K Temperature (K) Electric resitivity ( cm) log scale Electric resitivity ( cm) Temperature dependence of electrical conductivity in metals and semiconductors Temperature (K) • Resistivity of metals increases with temperature due to electron scattering by phonon • Resistivity of semiconductors decreases drastically with temperature due to increase in carrier concentration

Conductivity, carrier concentration, mobility • Relation between conductivity and carrier concentration n and mobility 　 = ne • Resistivity and conductivity is related by =1/ • Mobility is average velocity v[cm/s] introduced by electric field E[V/cm] , expressed by equation v= E

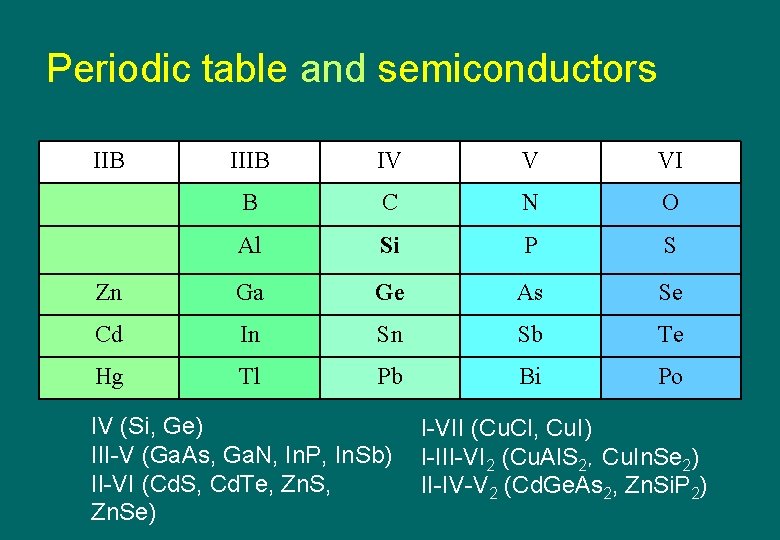
Periodic table and semiconductors IIB IV V VI B C N O Al Si P S Zn Ga Ge As Se Cd In Sn Sb Te Hg Tl Pb Bi Po IV (Si, Ge) III-V (Ga. As, Ga. N, In. P, In. Sb) II-VI (Cd. S, Cd. Te, Zn. Se) I-VII (Cu. Cl, Cu. I) I-III-VI 2 (Cu. Al. S 2，Cu. In. Se 2) II-IV-V 2 (Cd. Ge. As 2, Zn. Si. P 2)

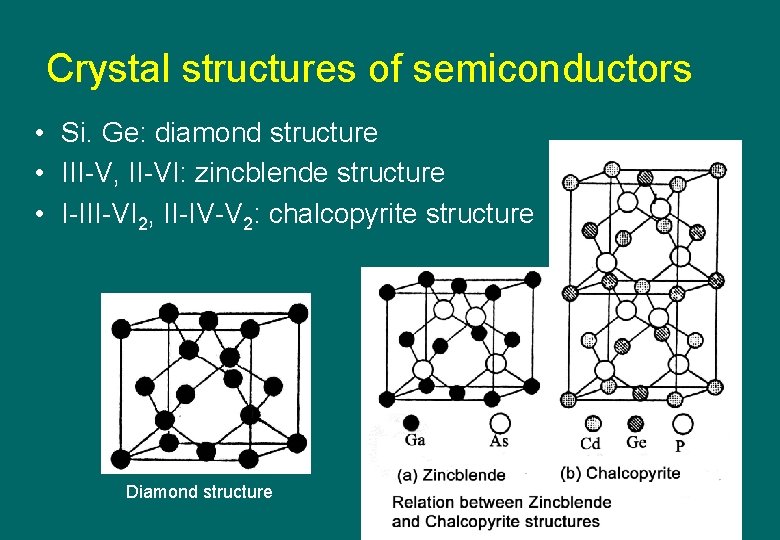
Crystal structures of semiconductors • Si. Ge: diamond structure • III-V, II-VI: zincblende structure • I-III-VI 2, II-IV-V 2: chalcopyrite structure Diamond structure

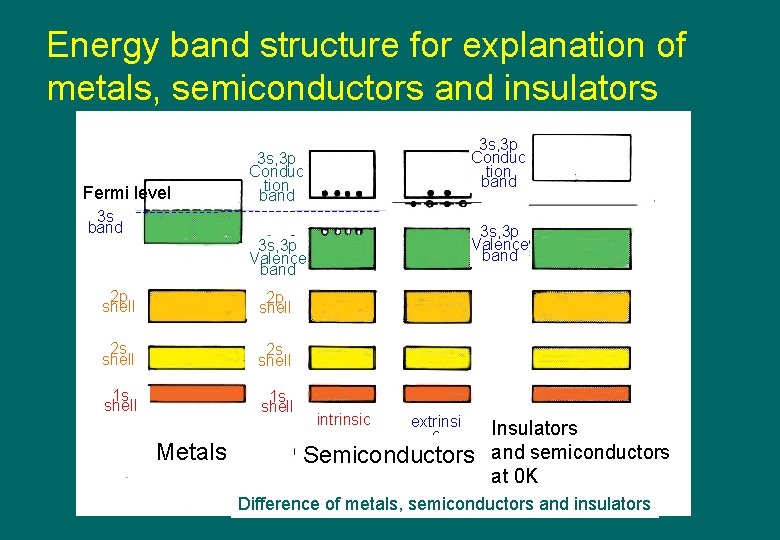
Energy band structure for explanation of metals, semiconductors and insulators Fermi level 3 s, 3 p Conduc tion band 3 s, 3 p Valence band 2 p shell 2 s shell 1 s shell Metals intrinsic extrinsi c Semiconductors Insulators and semiconductors at 0 K Difference of metals, semiconductors and insulators

Concept of Energy Band Two approaches • Approximation from free electron – Hartree-Fock approximation – Electron is treated as plane waves with wavenumber k – Energy E=( k)2/2 m (parabolic band) • Approximation from isolated atoms – Heitler-London approximation – Linear combination of s, p, d wavefunctions

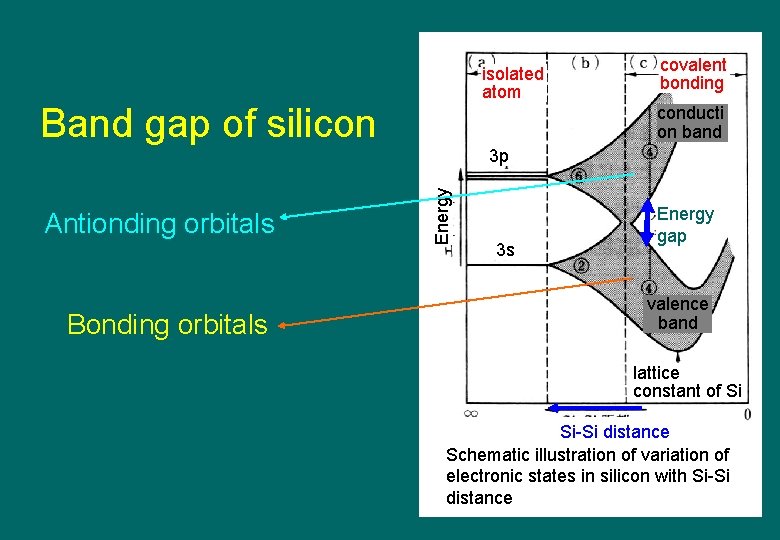
isolated atom Band gap of silicon covalent bonding conducti on band Antionding orbitals Bonding orbitals Energy 3 p 3 s Energy gap valence band lattice constant of Si Si-Si distance Schematic illustration of variation of electronic states in silicon with Si-Si distance

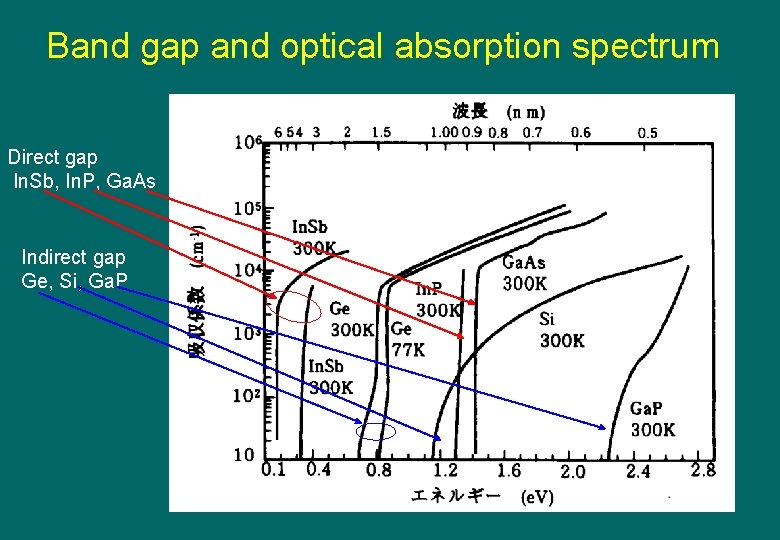
Band gap and optical absorption spectrum Direct gap In. Sb, In. P, Ga. As Indirect gap Ge, Si, Ga. P

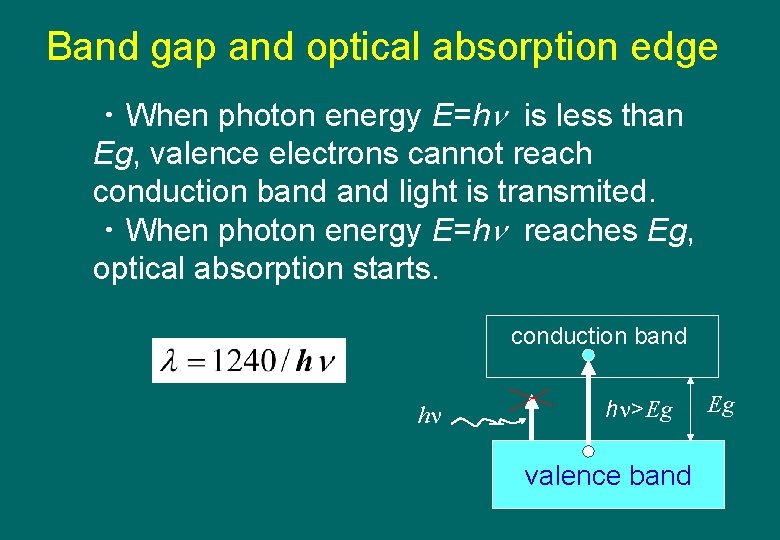
Band gap and optical absorption edge ・When photon energy E=h is less than Eg, valence electrons cannot reach conduction band light is transmited. ・When photon energy E=h reaches Eg, optical absorption starts. conduction band h h >Eg valence band Eg

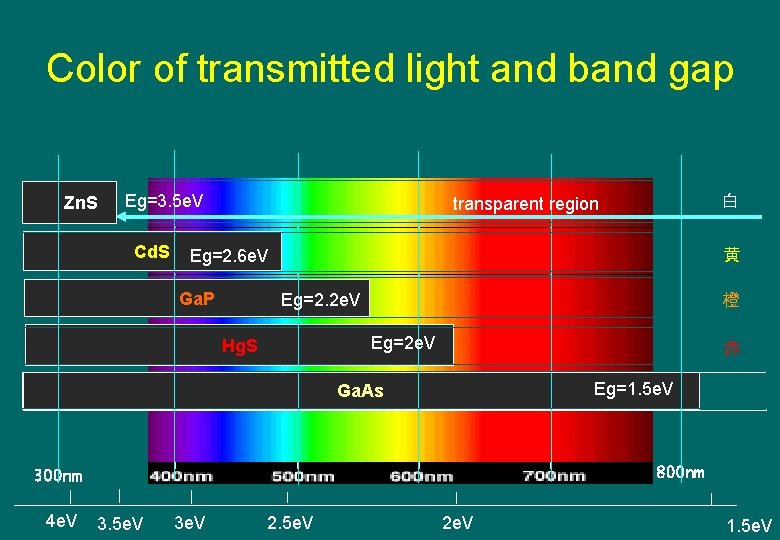
Color of transmitted light and band gap 　　Zn. S Eg=3. 5 e. V Cd. S 黄 Eg=2. 6 e. V Ga. P 橙 Eg=2. 2 e. V Eg=2 e. V Hg. S 赤 Eg=1. 5 e. V Ga. As 黒 800 nm 300 nm 4 e. V 白 transparent region 3. 5 e. V 3 e. V 2. 5 e. V 2 e. V 1. 5 e. V

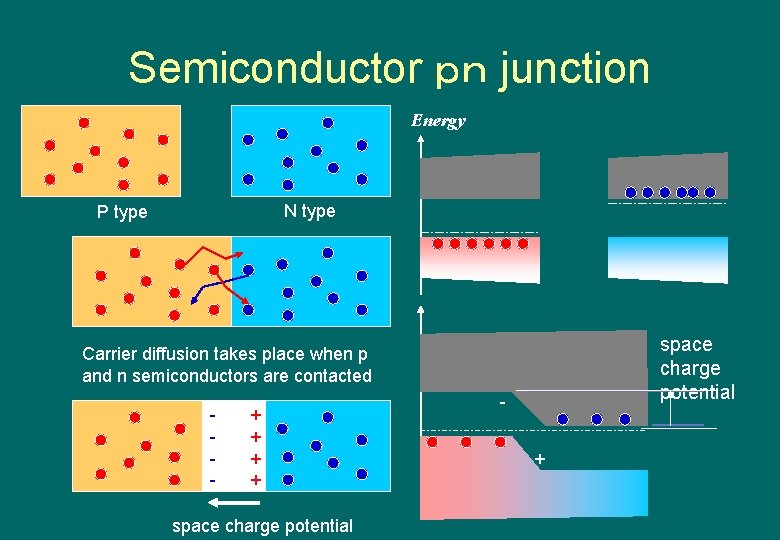
Semiconductor ｐｎ junction Energy N type P type space charge potential Carrier diffusion takes place when p and n semiconductors are contacted - + + space charge potential +

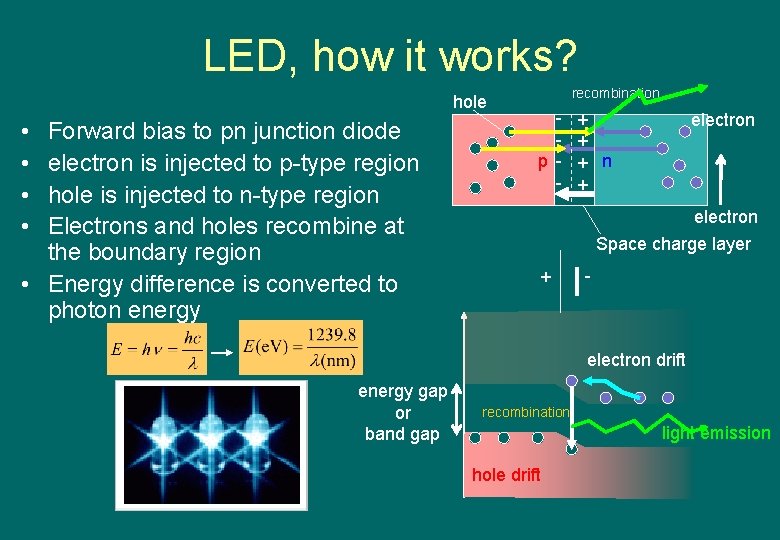
LED, how it works? hole • • Forward bias to pn junction diode electron is injected to p-type region hole is injected to n-type region Electrons and holes recombine at the boundary region • Energy difference is converted to photon energy recombination p - + + + n + electron Space charge layer + - electron drift energy gap or band gap recombination light emission hole drift

Semiconductors for LD • Optical communication： 1. 5 m; Ga. In. As. Sb, In. Ga. As. P • CD： 780 nm　Ga. As • DVD： 650 nm Ga. Al. As MQW • DVR： 405 nm In. Ga. N MQW

Double hetero structure • Electrons, holes and photons are confined in thin active layer by using the hetrojunction structure http: //www. ece. concordia. ca/ ~i_statei/vlsi-opt/

Invention of DH structure (1) • Herbert Kroemer and Zhores Alferov suggested in 1963 that the concentration of electrons, holes and photons would become much higher if they were confined to a thin semiconductor layer between two others - a double heterojunction. • Despite a lack of the most advanced equipment, Alferov and his co-workers in Leningrad (now St. Petersburg) managed to produce a laser that effectively operated continuously and that did not require troublesome cooling. • This was in May 1970, a few weeks earlier than their American competitors. • from Nobel Prize Presentation Speech in Physics 2000

Invention of DH structure (2) • In 1970, Hayashi and Panish at Bell Labs and Alferov in Russia obtained continuous operation at room temperature using double heterojunction lasers consisting of a thin layer of Ga. As sandwiched between two layers of Alx. Ga 1 -x. As. This design achieved better performance by confining both the injected carriers (by the band-gap discontinuity) and emitted photons (by the refractive-index discontinuity). • The double-heterojunction concept has been modified and improved over the years, but the central idea of confining both the carriers and photons by heterojunctions is the fundamental philosophy used in all semiconductor lasers. from Physics and the communications industry W. F. Brinkman and D. V. Lang Bell Laboratories, Lucent Technologies, Murray Hill, New Jersey 07974 http: //www. bellsystemmemorial. com/pdf/physics_com. pdf