Introduction to Numerical Methods 1 What is a

Introduction to Numerical Methods 1

What is a Numerical Method (NM)? ØA method of solving complex engineering problems when analytical methods fail to provide a solution. Ø Opposite of NM is Analytical Method. 2

Problem: Solve the equation: x 2 - 3 x + 2 = 0 Solutions: a) Analytical Method: Using the formula we get 3

NUMERICAL METHOD Step 1: Rewrite the equation as x = (x 2 + 2)/3 Step 2: Start with some initial solution, say x = 0 Step 3: Using the equation in Step 1, determine x (Here x = 2/3) Step 4: Use this value of x to determine the next approximation. Step 5: Repeat the process until two successive values are almost the same. 4

Result: With the equation x = (x 2 + 2)/3 and the initial value x = 0, the successive solutions computed are as follows: 0, 0. 6667, 0. 8148, 0. 8880, 0. 9295, 0. 9547, 0. 9705, 0. 9806, 0. 9872, 0. 9915, 0. 9944, 0. 9963, 0. 9975, 0. 9983, 0. 9989, 0. 9993, 0. 9995, …. . 5

Important issues in NM accuracy precision errors APPROXIMATION significant condition stability figures 6

Accuracy vs. Bias Ø Accuracy: “…how closely a computed value agrees with the true value” Ø Bias/Inaccuracy : “…a systematic deviation from the truth” vs. Accurate 7 Biased/Inaccurate

Precision vs. Uncertainty Ø Precision : “…how closely individual computed values agree with each other” Ø Uncertainty/Imprecision : “…magnitude of scatter” vs. 8 Precise Uncertain/Imprecise

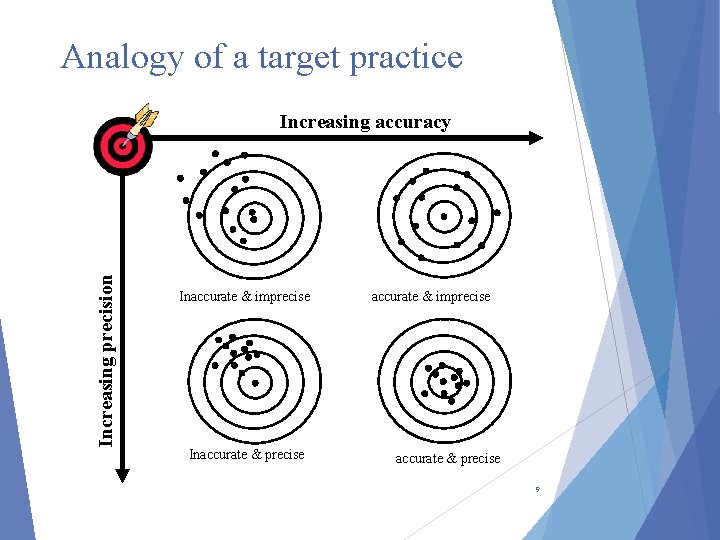
Analogy of a target practice Increasing precision Increasing accuracy Inaccurate & imprecise Inaccurate & precise accurate & imprecise accurate & precise 9

Types of Errors are of two types: 1. Truncation Error 2. Round-off Error Truncation error is a result of using approximations to represent exact mathematical procedures. Round-off error occurs when only certain digits and decimal places are used to represent exact numbers. 10

Example 1: 1. We know that Suppose we use it to evaluate sin 30°. x = 30°= /6 0. 5236 Our first approximation is sin 30° 0. 5236. 11

Second approximation: sin 30° 0. 5236 - 0. 52363/6 = 0. 499675 Third approximation: sin 30° 0. 499675+0. 52365/120 =0. 5000029570 The error involved in the approximations here is truncation error, since terms in the approximating series are truncated. 12

Example 2: Consider the number 3. 12746 If the number is written correct to 3 decimal places, then it is approximated as 3. 127 If the number is written correct to 4 decimal places, then it is approximated as 3. 1275 The error involved in this kind of approximation is called round-off error. 13

Measurement of Errors: Precision and accuracy are important criteria for the assessment of approximate solutions. There are formulae to measure these characteristics. When the current solution is compared with the true solution, the error involved is called true error. When the current solution is compared with the solution obtained in the previous iteration, the error involved is called approximate error. 14

1. True Error: • It is used to measure the lack of accuracy of an estimate. • True (absolute) error = Et = True value – Approximation • True relative error = Et /True value 15

True percent relative error = t Usually this is expressed as an absolute value (i. e. , without any sign) 16

Approximate Error: • used to measure the lack of precision of an estimate. • Approximate (absolute) error Ea = Current approximation - Previous approximation • Approximate relative error = Ea/Current app 17

Approximate percent relative error = a Usually this is also expressed as an absolute value (i. e. , without any sign) 18

Significant Figures Ø • Usually computation is repeated until the approximate percent relative error (| a| ) is within the pre-specified acceptable level ( denoted by s ) i. e. , until | a|< s • s is usually determined by specifying the number of significant figures required. • If the number of significant figures required is at least n, then s must be (0. 5 10 2 -n)% 19

Example: Suppose we wish to get the result of a computation correct to 3 significant figures i. e. , n = 3 Here we must fix s as s = 0. 5 10 2 -3 % = 0. 05% It means that we must improve our estimate until | a| becomes less than 0. 05 20

Suppose our first two estimates are 1. 23456 and 1. 23785. Since | a| is more than s , we must continue the iteration. 21

Suppose third estimate is 1. 23812. Error is now estimated as Now we see that | a| is less than s. Hence we have got the precision required and we can stop the iteration. 22

Quick Notes on Taylor Series The Taylor expansion about x=a, is given as with Is called as the remainder or error of the Taylor series 23

If a=0, the Taylor series is known as Maclaurin series. 24

or 25

Example 3 Solution. Thus 26

Example 4 Find the Taylor series of sin(x) about x=0. Solution: 27

This pattern will repeat. Thus the Taylor series for sin(x) about x=0 is Exercise. Find the Taylor series for f(x)=cos(x) about x=0 and x=pi/4. 28