Introduction to Number Representation n Binary Numbers n

Introduction to Number Representation n Binary Numbers n Sign/Magnitude n 2 s Complement A Level Computer Science

Binary

Binary n All computer processing is carried out digitally. n This means that the processor handles instructions as binary codes – zeros and ones. n All data on a PC is essentially 0’s and 1’s.

Converting binary into positive denary integers n Whole positive denary (base ten) numbers are converted into binary as follows: n 135 from denary into binary 128 + 4 + 2 + 1 = 135 MSB 128 64 32 16 1 0 0 0 LSB 8 0 4 1 2 1 1 1

The repeated division method A method for converting denary to binary: 98 in denary into binary: 98 divide by 2 = 49 remainder 0 49 divide by 2 = 24 remainder 1 24 divide by 2 = 12 remainder 0 12 divide by 2 = 6 remainder 0 6 divide by 2 = 3 remainder 0 3 divide by 2 = 1 remainder 1 1 divide by 2 = 0 remainder 1 0 divide by 2 = 0 remainder 0 DIV MOD Read the binary code from the remainder from bottom to the top: 01100010 which equals 98

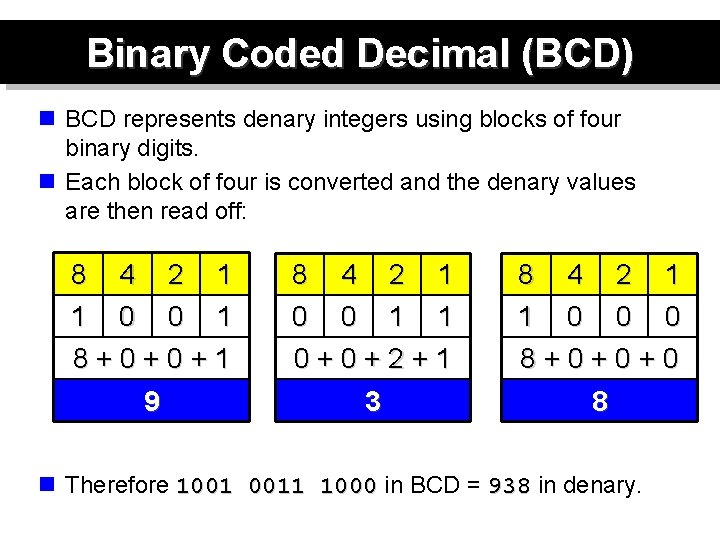
Binary Coded Decimal (BCD) n BCD represents denary integers using blocks of four binary digits. n Each block of four is converted and the denary values are then read off: 8 1 4 0 2 0 1 1 8+0+0+1 9 8 0 4 0 2 1 1 1 0+0+2+1 3 8 1 4 0 2 0 1 0 8+0+0+0 8 n Therefore 1001 0011 1000 in BCD = 938 in denary.

Uses of BCD n BCD enables fast conversions from denary to binary for applications such as pocket calculators. n Each digit on a calculator corresponds directly to a four-bit block in BCD.

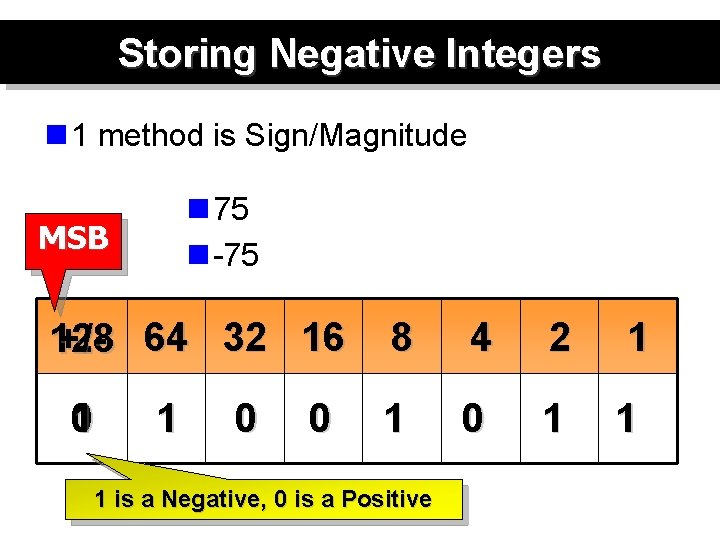
Storing Negative Integers n 1 method is Sign/Magnitude n 75 n -75 MSB 128 +/- 64 32 16 1 0 0 8 4 2 1 1 0 1 1 1 is a Negative, 0 is a Positive

Sign/Magnitude n This method has some limitations n Makes calculations difficult by losing 1 bit 127 maximum number +/- 64 32 16 0 Sign 1 0 0 8 4 2 1 1 0 1 1 Value or Magnitude

Storing Negative Integers n Another method is 2 s Complement n -75 128 64 32 16 -128 1 0 1 1 8 4 2 1 0 1 n-128+32+16+4+1=-75

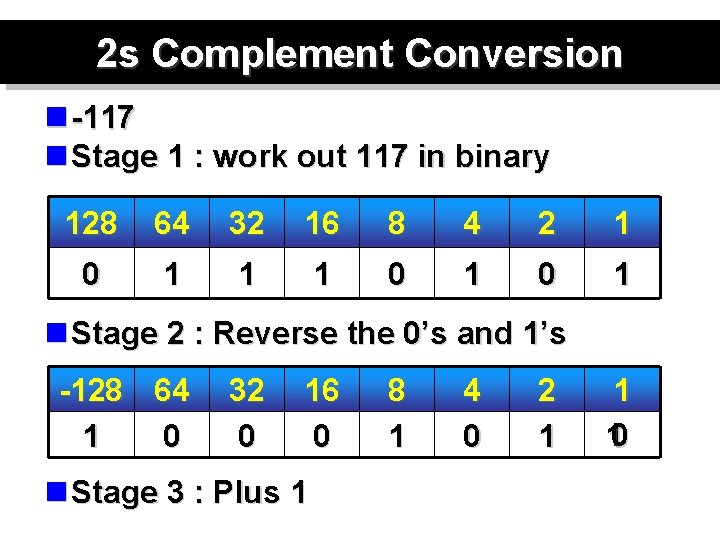
2 s Complement Conversion n -117 n Stage 1 : work out 117 in binary 128 64 32 16 8 4 2 1 0 1 1 1 0 1 n Stage 2 : Reverse the 0’s and 1’s -128 64 1 0 32 0 16 0 n Stage 3 : Plus 1 8 1 4 0 2 1 1 10

Representing characters n There are three main coding systems that provide conversions of keyboard characters into binary: –EBCDIC –ASCII –UNICODE

EBCDIC n EBCDIC stands for Extended Binary Coded Decimal Interchange Code. n It is an extension of BCD which includes non-numeric characters, including all the keyboard characters and special characters. n It is commonly used to encode data onto magnetic tape.

ASCII n ASCII stands for the American Standard Code for Information Interchange. n It has been adopted as the industrystandard way of representing keyboard characters as binary codes. n Every keyboard character is given a corresponding binary code. n ASCII uses an 8 -bit code to provide 256 characters.

UNICODE n UNICODE is the new standard to emerge that is replacing ASCII. n It has been adopted by many of the big businesses in the computing industry. n It is designed to cover more of the characters that are found in languages across the world. n It has become important due to the increased use of the Internet, as more data is being passed around globally.