Introduction to Nuclear physics The nucleus a complex

Introduction to Nuclear physics; The nucleus a complex system Héloïse Goutte GANIL Caen, France goutte@ganil. fr Héloïse Goutte CERN Summer student program 2010 1

The nucleus : a complex system I) Some features about the nucleus discovery radius binding energy nucleon-nucleon interaction life time applications II) Modeling of the nucleus liquid drop shell model mean field III) Examples of recent studies exotic nuclei isomers shape coexistence super heavy IV) Toward a microscopic description of the fission process Héloïse Goutte CERN Summer student program 2010 2

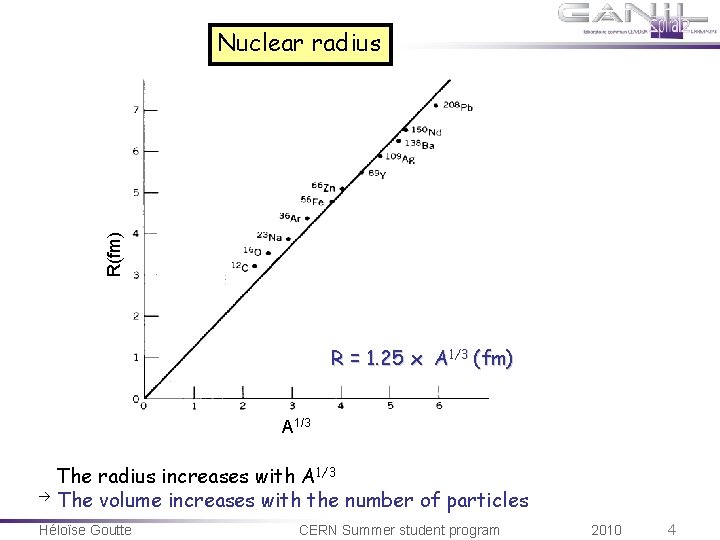
R(fm) Nuclear radius R = 1. 25 x A 1/3 (fm) A 1/3 The radius increases with A 1/3 The volume increases with the number of particles Héloïse Goutte CERN Summer student program 2010 4

Binding energy Mass of a given nucleus : M(A, Z) = N Mn + Z Mp – B(A, Z) : binding energy Stable bound system for B > 0 (its mass is lower than the mass of its components) Unstable systems : they transform into more stable nuclei Exponential decay Half –life T defined as the time for which the number of remaining nuclei is half of its the initial value. Héloïse Goutte CERN Summer student program 2010 6

II) Modeling of the nucleus Héloïse Goutte CERN Summer student program 2010 10

The nucleus : a liquid drop ? The nucleus and its features, radii, and binding energies have many similarities with a liquid drop : The volume of a drop is proportional to its number of molecules. There are no long range correlations between molecules in a drop. -> Each molecule is only sensitive to the neighboring molecules. -> Description of the nucleus in term of a model of a charged liquid drop Héloïse Goutte CERN Summer student program 2010 11 11

The liquid drop model * Model developed by Von Weizsacker and N. Bohr (1937) It has been first developed to describe the nuclear fission. * The nucleus is represented by a charged liquid drop. * The model has been used to predict the main properties of the nuclei such as: * nuclear radii, * nuclear masses and binding energies, * decay out, * fission. * The binding energy of the nuclei is described by the Bethe Weizsacker formula Héloïse Goutte CERN Summer student program 2010 12

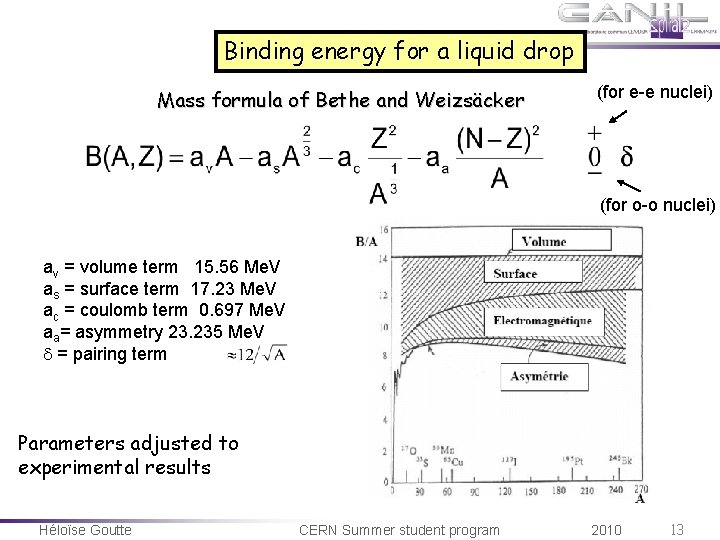
Binding energy for a liquid drop Mass formula of Bethe and Weizsäcker (for e-e nuclei) (for o-o nuclei) av = volume term 15. 56 Me. V as = surface term 17. 23 Me. V ac = coulomb term 0. 697 Me. V aa= asymmetry 23. 235 Me. V = pairing term Parameters adjusted to experimental results Héloïse Goutte CERN Summer student program 2010 13

Problems with the liquid drop model 1) Nuclear radii Evolution of mean square radii with respect to 198 Hg as a function of neutron number. Light isotopes are unstable nuclei produced at CERN by use of the ISOLDE apparatus. -> some nuclei away from the A 2/3 law Fig. from http: //ipnweb. in 2 p 3. fr/recherche Héloïse Goutte CERN Summer student program 2010 14

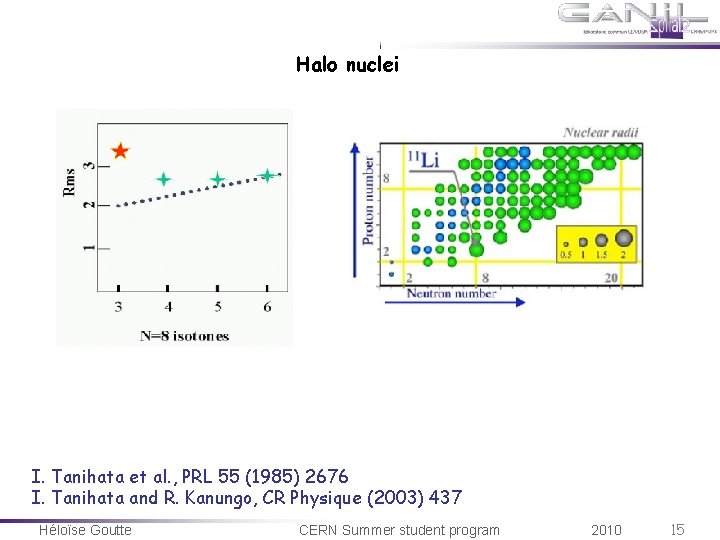
Halo nuclei I. Tanihata et al. , PRL 55 (1985) 2676 I. Tanihata and R. Kanungo, CR Physique (2003) 437 Héloïse Goutte CERN Summer student program 2010 15

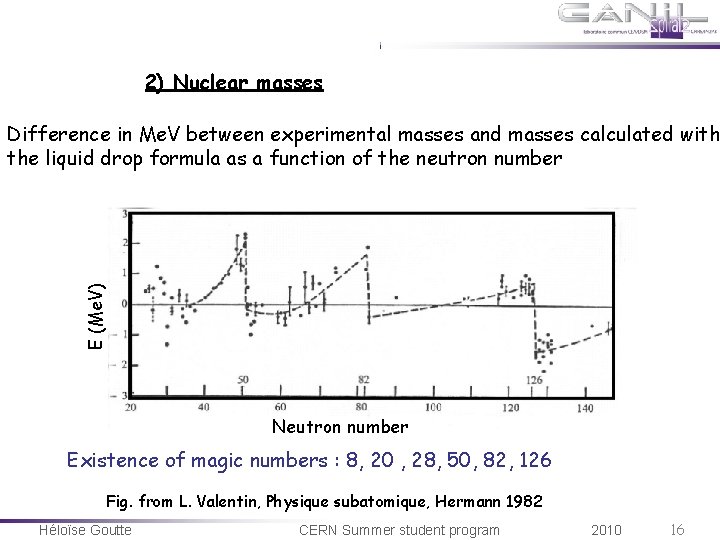
2) Nuclear masses E (Me. V) Difference in Me. V between experimental masses and masses calculated with the liquid drop formula as a function of the neutron number Neutron number Existence of magic numbers : 8, 20 , 28, 50, 82, 126 Fig. from L. Valentin, Physique subatomique, Hermann 1982 Héloïse Goutte CERN Summer student program 2010 16

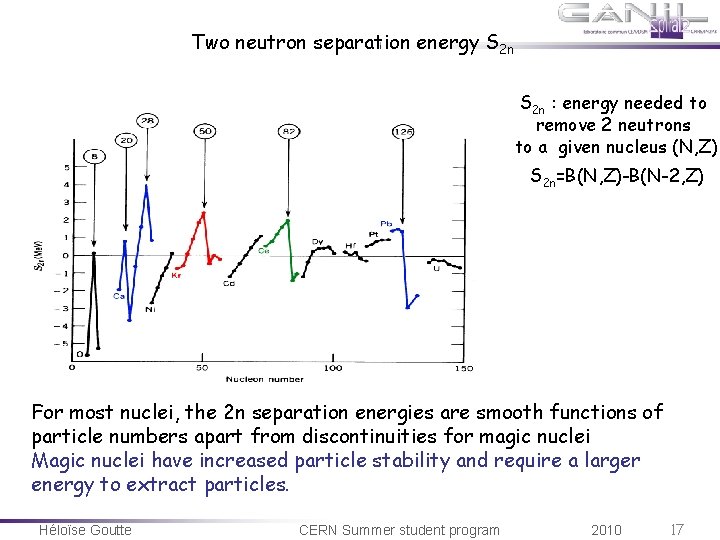
Two neutron separation energy S 2 n : energy needed to remove 2 neutrons to a given nucleus (N, Z) S 2 n=B(N, Z)-B(N-2, Z) For most nuclei, the 2 n separation energies are smooth functions of particle numbers apart from discontinuities for magic nuclei Magic nuclei have increased particle stability and require a larger energy to extract particles. Héloïse Goutte CERN Summer student program 2010 17

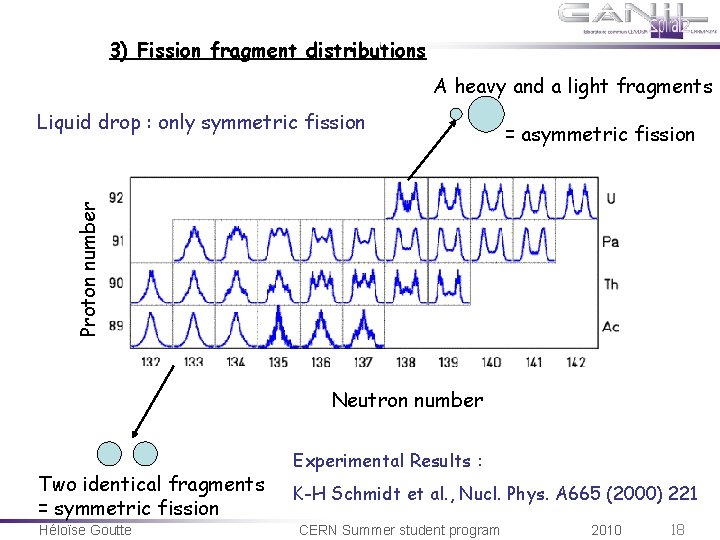
3) Fission fragment distributions A heavy and a light fragments = asymmetric fission Proton number Liquid drop : only symmetric fission Neutron number Two identical fragments = symmetric fission Héloïse Goutte Experimental Results : K-H Schmidt et al. , Nucl. Phys. A 665 (2000) 221 CERN Summer student program 2010 18

The nucleus is not a liquid drop : structure effects There are many « structure effects » in nuclei, that can not be reproduced by macroscopic approaches like the liquid drop model There are «magic numbers» 2, 8, 20, 28, 50, 82, 126 and so «magic» and «doubly magic» nuclei -> need for microscopic approaches, for which the fundamental ingredients are the nucleons and the interaction between them Héloïse Goutte CERN Summer student program 2010 19

Microscopic description of the atomic nucleus Nucleus = N nucleons in strong interaction The many-body problem (the behavior of each nucleon influences the others) Nucleon-Nucleon force unknown Can be solved exactly for N < 4 For N >> 10 : approximations Shell model • only a small number of particles are active Héloïse Goutte Different forces used depending on the method chosen to solve the Many-body problem Approaches based on the mean field • no inert core • but not all the correlations between particles are taken into account CERN Summer student program 2010 20

Quantum mechanics Nucleons are quantum objects : Only some values of the energy are available : a discrete number of states Nucleons are fermions : Two nucleons can not occupy the same quantum state : the Pauli principle Héloïse Goutte Neutrons Protons CERN Summer student program 2010 21

The Goeppert Mayer shell model * Model developped by M. Goeppert Mayer in 1948 : The shell model of the nucleus describes the nucleons in the nucleus in the same way as electrons in the atom. * “In analogy with atomic structure one may postulate that in the nucleus the nucleons move fairly independently in individual orbits in an average potential …” , M. Goeppert Mayer, Nobel Conference 1963. Héloïse Goutte CERN Summer student program 2010 22

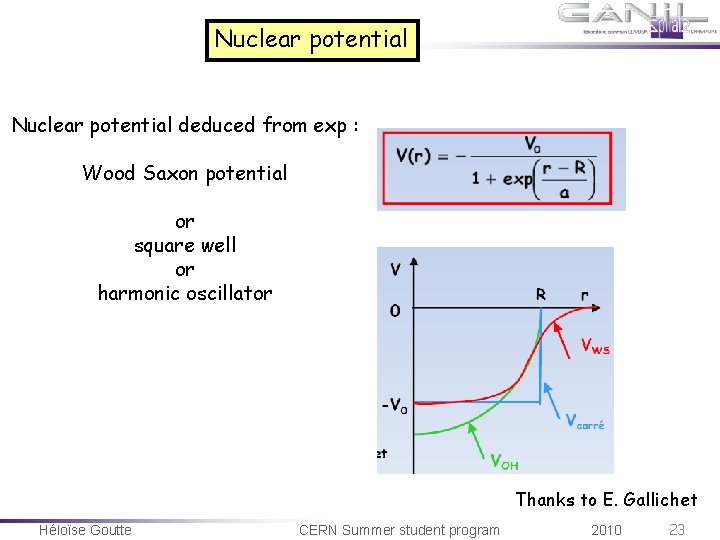
Nuclear potential deduced from exp : Wood Saxon potential or square well or harmonic oscillator Thanks to E. Gallichet Héloïse Goutte CERN Summer student program 2010 23

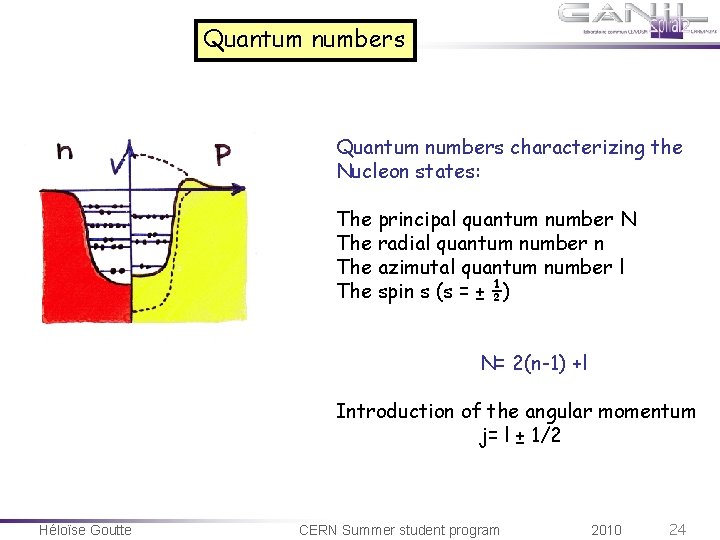
Quantum numbers characterizing the Nucleon states: The principal quantum number N The radial quantum number n The azimutal quantum number l The spin s (s = ± ½) N= 2(n-1) +l Introduction of the angular momentum j= l ± 1/2 Héloïse Goutte CERN Summer student program 2010 24

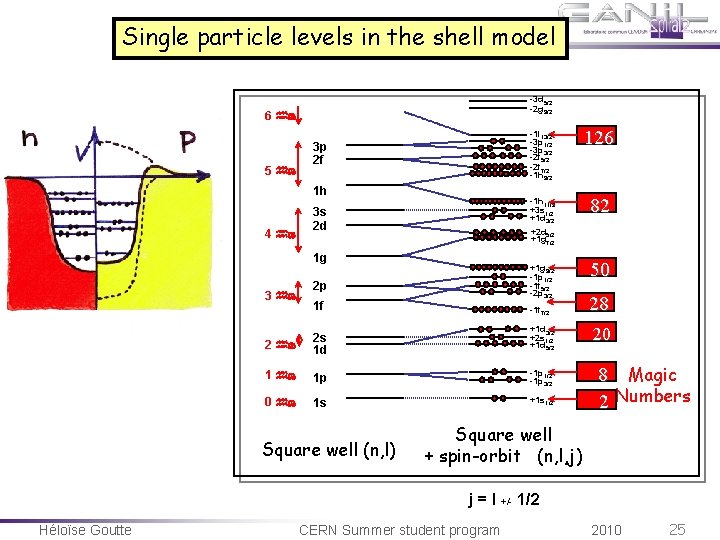
Single particle levels in the shell model -3 d 5/2 -2 g 9/2 6 hw 5 hw 3 p 2 f 1 h 4 hw 3 s 2 d 126 -1 h 11/2 +3 s 1/2 +1 d 3/2 82 +2 d 5/2 +1 g 7/2 1 g 3 hw -1 i 13/2 -3 p 1/2 -3 p 3/2 -2 f 5/2 -2 f 7/2 -1 h 9/2 +1 g 9/2 -1 p 1/2 -1 f 5/2 -2 p 3/2 2 p 1 f -1 f 7/2 +1 d 3/2 +2 s 1/2 +1 d 5/2 2 hw 2 s 1 d 1 hw 1 p -1 p 1/2 -1 p 3/2 0 hw 1 s +1 s 1/2 Square well (n, l) 50 28 20 8 Magic 2 Numbers Square well + spin-orbit (n, l, j) j = l +/- 1/2 Héloïse Goutte CERN Summer student program 2010 25

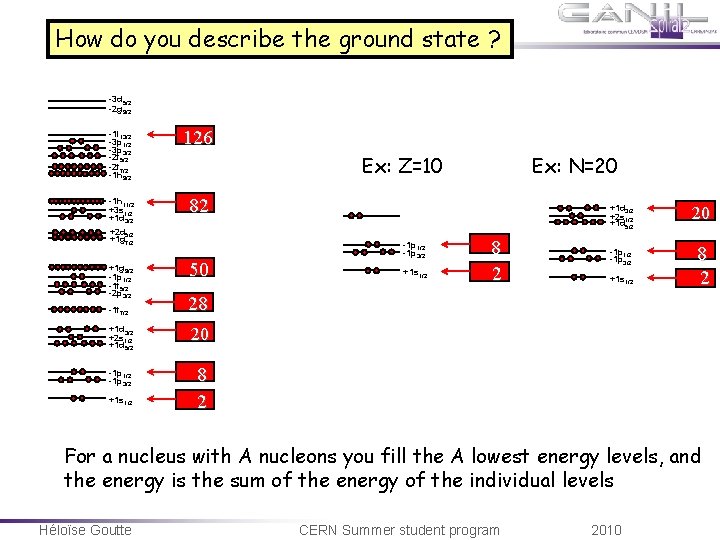
How do you describe the ground state ? -3 d 5/2 -2 g 9/2 -1 i 13/2 -3 p 1/2 -3 p 3/2 -2 f 5/2 -2 f 7/2 -1 h 9/2 126 -1 h 11/2 +3 s 1/2 +1 d 3/2 82 Ex: Z=10 +2 d 5/2 +1 g 7/2 +1 g 9/2 -1 p 1/2 -1 f 5/2 -2 p 3/2 -1 f 7/2 50 +1 s 1/2 8 2 +1 d 3/2 +2 s 1/2 +1 d 5/2 20 -1 p 1/2 -1 p 3/2 8 2 +1 s 1/2 28 +1 d 3/2 +2 s 1/2 +1 d 5/2 20 -1 p 1/2 -1 p 3/2 8 2 +1 s 1/2 -1 p 3/2 Ex: N=20 For a nucleus with A nucleons you fill the A lowest energy levels, and the energy is the sum of the energy of the individual levels Héloïse Goutte CERN Summer student program 2010

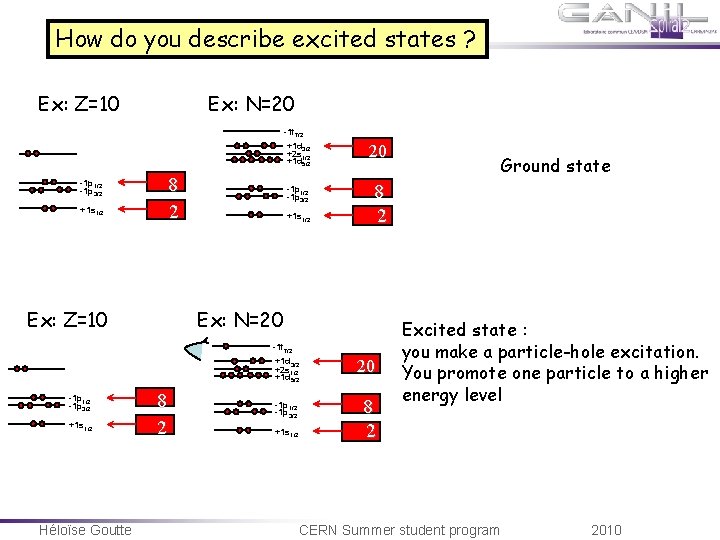
How do you describe excited states ? Ex: Z=10 Ex: N=20 -1 f 7/2 -1 p 1/2 -1 p 3/2 +1 s 1/2 8 2 Ex: Z=10 +1 d 3/2 +2 s 1/2 +1 d 5/2 20 -1 p 1/2 -1 p 3/2 8 2 +1 s 1/2 Ex: N=20 -1 f 7/2 -1 p 1/2 -1 p 3/2 +1 s 1/2 Héloïse Goutte 8 2 +1 d 3/2 +2 s 1/2 +1 d 5/2 20 -1 p 1/2 -1 p 3/2 8 2 +1 s 1/2 Ground state Excited state : you make a particle-hole excitation. You promote one particle to a higher energy level CERN Summer student program 2010

Beyond this “independent particle shell model” Satisfying results for magic nuclei : ground state and low lying excited states Problems : • Neglect of collective excitations • Same potential for all the nucleons and for all the configurations • Independent particles • Improved shell model (currently used): The particles are not independent : due to their interactions with the other particles they do not occupy a given orbital but a sum of configurations having a different probability. -> definition of a valence space where the particles are active Héloïse Goutte CERN Summer student program 2010 26

The shell model space Héloïse Goutte CERN Summer student program 2010 27

Héloïse Goutte CERN Summer student program 2010 28

The self consistent mean field approach Main assumption: each particle is interacting with an average field generated by all the other particles : the mean field The mean field is built from the individual excitations between the nucleons Self consistent mean field : the mean field is not fixed. It depends on the configuration. No inert core Héloïse Goutte CERN Summer student program 2010 29

The self consistent mean field approach The Hartree Fock method The basis ingredient is the Hamiltonian which governs the dynamics of the individual nucleons (equivalent to the total energy in classical physics) Effective force Wave function orbitals of the nucleons = antisymmetrized product of A with Orbitals are obtained by minimizing the total energy of the nucleus Héloïse Goutte CERN Summer student program 2010 30

The phenomenological effective finite-range Gogny force P : isospin exchange operator P : spin exchange operator Finite range central term Density dependent term Spin orbit term Coulomb term back Héloïse Goutte CERN Summer student program 2010 31

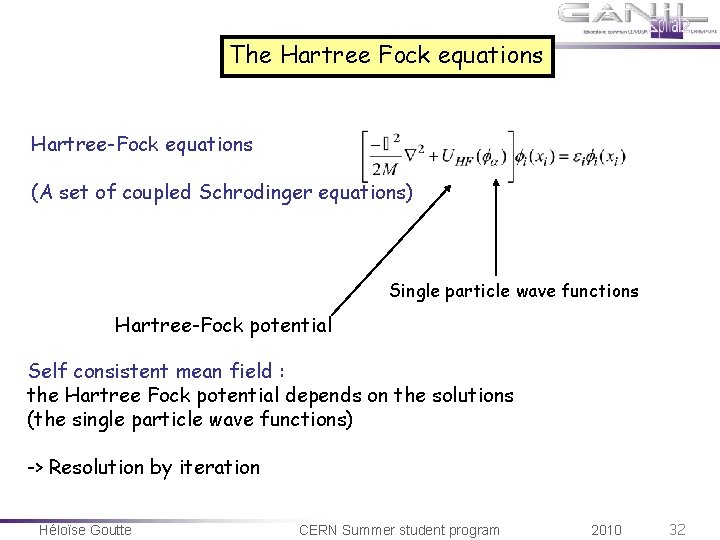
The Hartree Fock equations Hartree-Fock equations (A set of coupled Schrodinger equations) Single particle wave functions Hartree-Fock potential Self consistent mean field : the Hartree Fock potential depends on the solutions (the single particle wave functions) -> Resolution by iteration Héloïse Goutte CERN Summer student program 2010 32

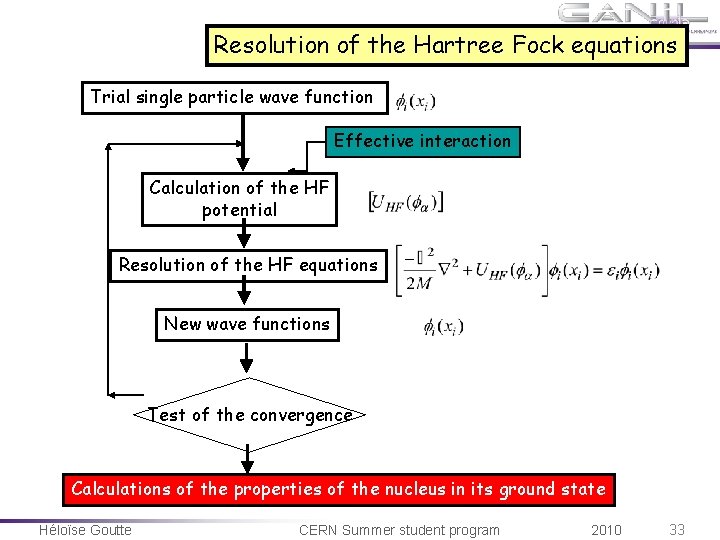
Resolution of the Hartree Fock equations Trial single particle wave function Effective interaction Calculation of the HF potential Resolution of the HF equations New wave functions Test of the convergence Calculations of the properties of the nucleus in its ground state Héloïse Goutte CERN Summer student program 2010 33

Deformation We can “measure” nuclear deformations as the mean values of the mutipole operators Spherical Harmonic If we consider the isoscalar axial quadrupole operator We find that: http: //www-phynu. cea. fr Most ot the nuclei are deformed in their ground state Magic nuclei are spherical Héloïse Goutte CERN Summer student program 2010 34

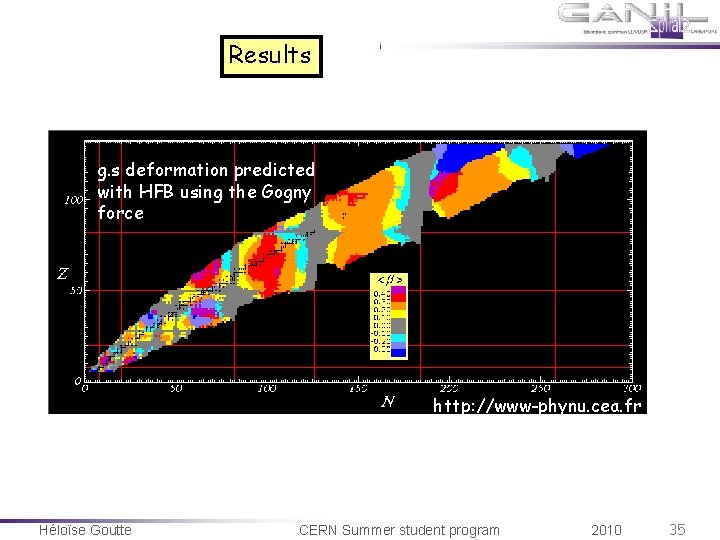
Results g. s deformation predicted with HFB using the Gogny force http: //www-phynu. cea. fr Héloïse Goutte CERN Summer student program 2010 35

Constraints Hartree-Fock-Bogoliubov calculations We can impose collective deformations and test the response of the nuclei with Where ’s are Lagrange parameters Héloïse Goutte CERN Summer student program 2010 36

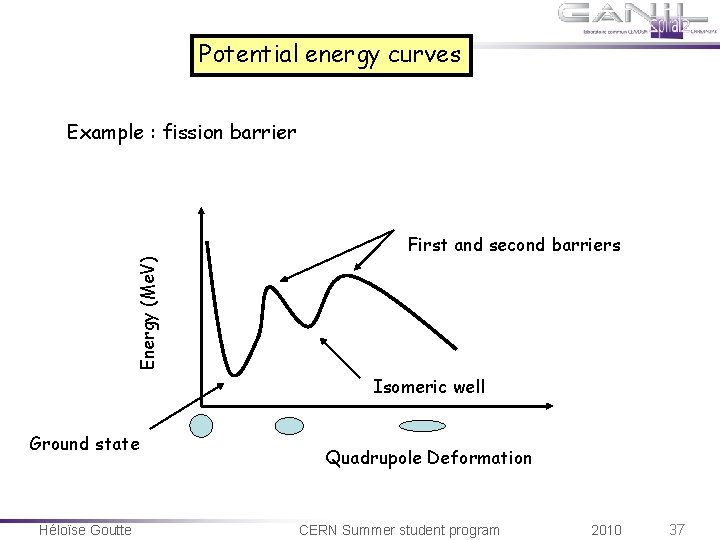
Potential energy curves Example : fission barrier Energy (Me. V) First and second barriers Isomeric well Ground state Héloïse Goutte Quadrupole Deformation CERN Summer student program 2010 37

What are the most commonly used constraints ? What are the problems with this deformation ? Héloïse Goutte CERN Summer student program 2010 38

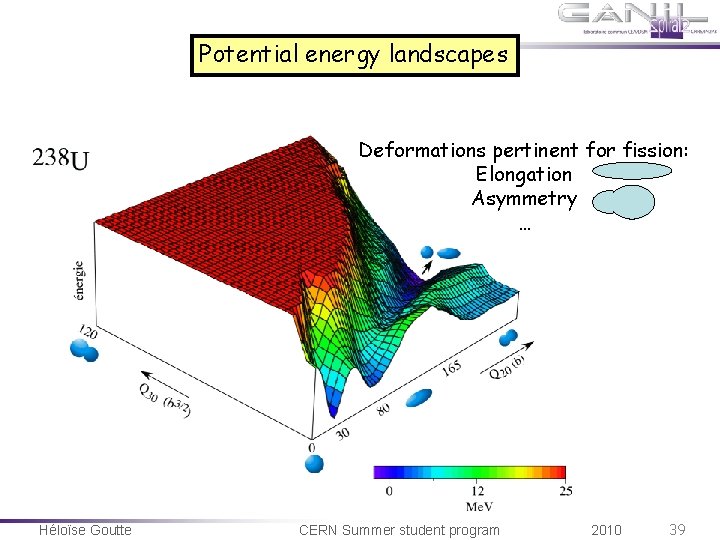
Potential energy landscapes Deformations pertinent for fission: Elongation Asymmetry … Héloïse Goutte CERN Summer student program 2010 39

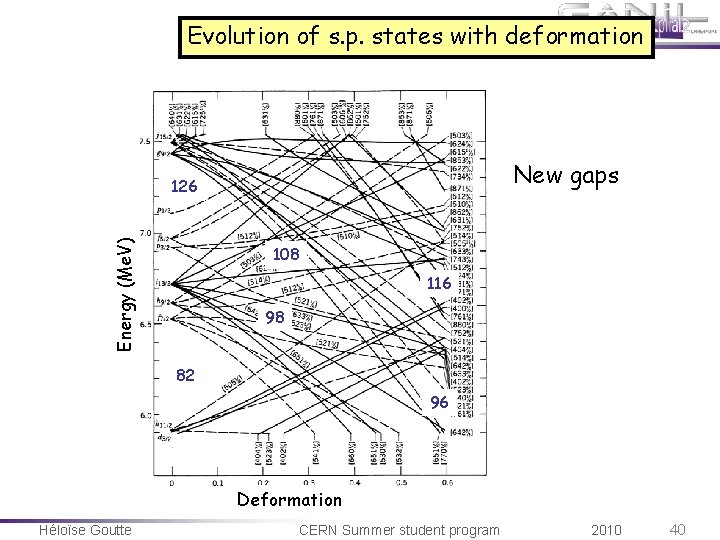
Evolution of s. p. states with deformation New gaps Energy (Me. V) 126 108 116 98 82 96 Deformation Héloïse Goutte CERN Summer student program 2010 40

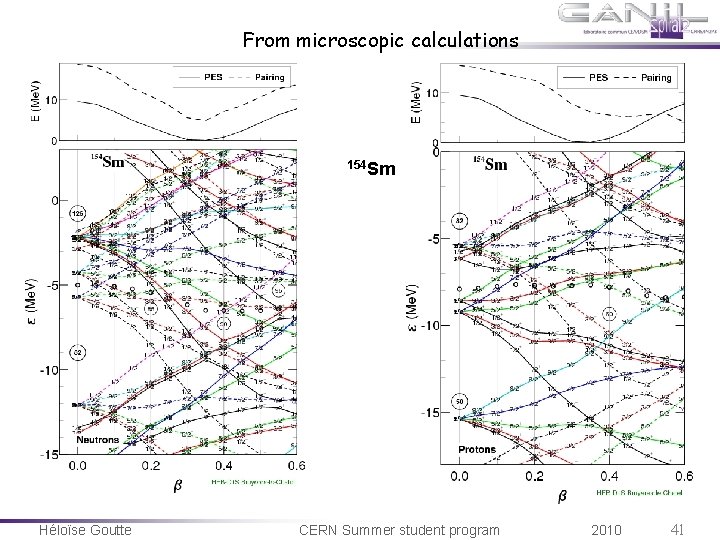
From microscopic calculations 154 Sm Héloïse Goutte CERN Summer student program 2010 41

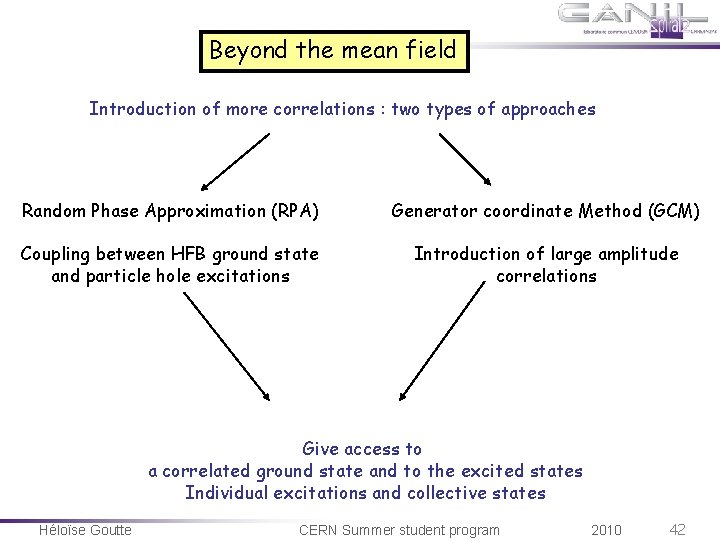
Beyond the mean field Introduction of more correlations : two types of approaches Random Phase Approximation (RPA) Generator coordinate Method (GCM) Coupling between HFB ground state and particle hole excitations Introduction of large amplitude correlations Give access to a correlated ground state and to the excited states Individual excitations and collective states Héloïse Goutte CERN Summer student program 2010 42

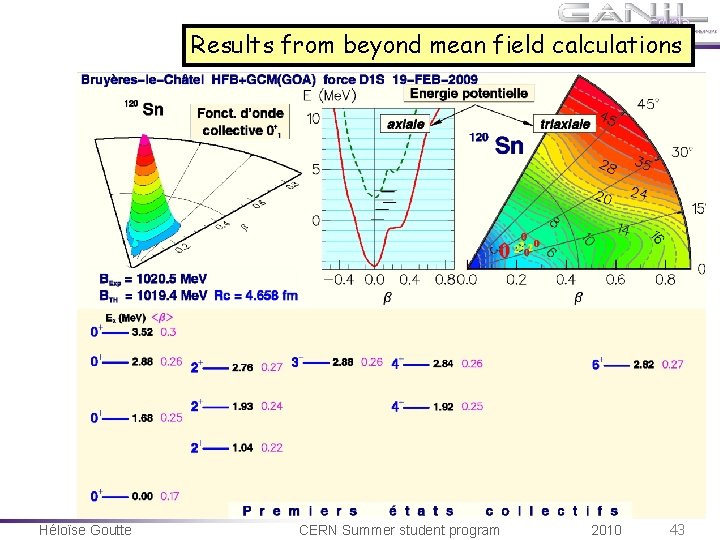
Results from beyond mean field calculations Héloïse Goutte CERN Summer student program 2010 43

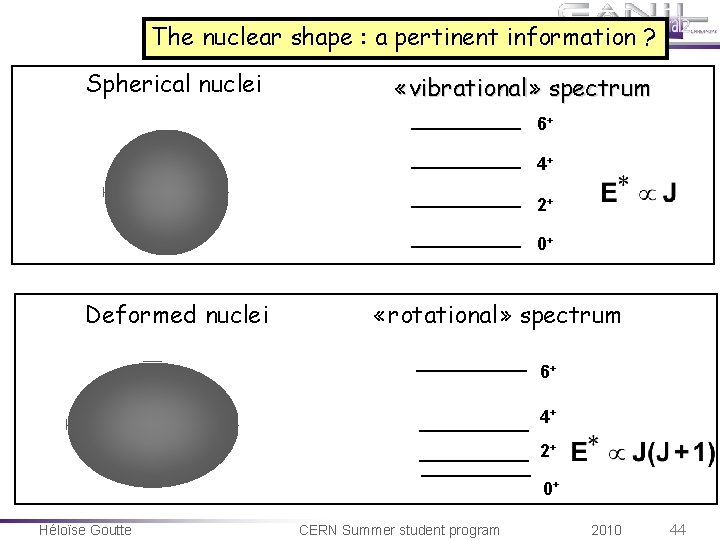
The nuclear shape : a pertinent information ? Spherical nuclei «vibrational» spectrum 6+ 4+ 2+ 0+ Deformed nuclei «rotational» spectrum 6+ 4+ 2+ 0+ Héloïse Goutte CERN Summer student program 2010 44

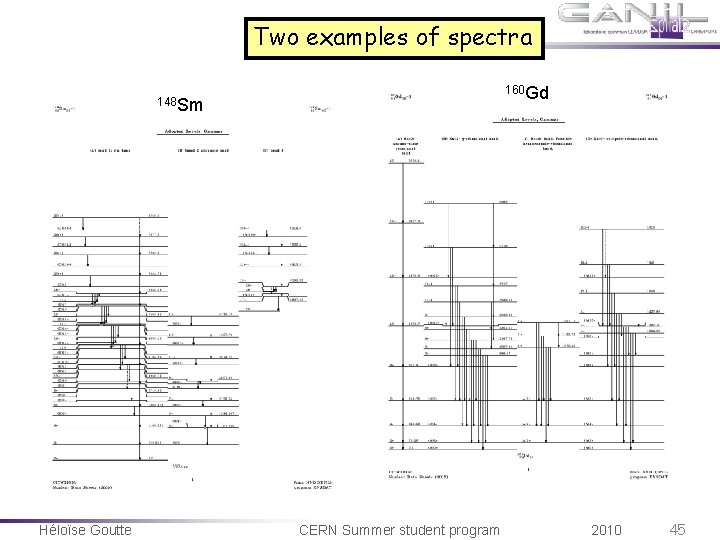
Two examples of spectra 160 Gd 148 Sm Héloïse Goutte CERN Summer student program 2010 45

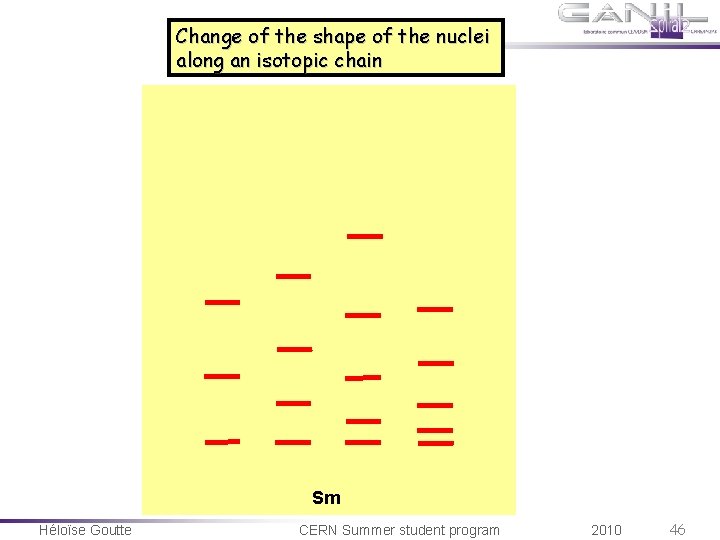
Change of the shape of the nuclei along an isotopic chain Sm Héloïse Goutte CERN Summer student program 2010 46

Angular velocity of a rotating nucleus For a rotating nucleus, the energy of a level is given by* : With J the moment of inertia We also have so With To compare with a wash machine: 1300 tpm * Mécanique quantique by C. Cohen-Tannoudji, B. Diu, F. Laloe) Héloïse Goutte CERN Summer student program 2010 47

Modeling of the nuclei : Summary • Macroscopic description of a nucleus : the liquid drop model • Microscopic description needed: the basic ingredients are the nucleons and the interaction between them. • Different microscopic approaches : the shell model and the mean field • Many nuclei are found deformed in their ground states • The spectroscopy strongly depends on the deformation Héloïse Goutte CERN Summer student program 2010 48