Introduction to Multigrid Method Presented by Bogojeska Jasmina

Introduction to Multigrid Method Presented by: Bogojeska Jasmina 09/09/2020 JASS, 2005, St. Petersburg 1

The ultimate upshot of MLAT • The amount of computational work should be proportional to the amount of real physical changes in the computed system! • In fully developped Multigrid processes the amount of computations should be determined only by the amount of real physical information 09/09/2020 JASS, 2005, St. Petersburg 2

Content • • Model Problems Basic Iterative Schemes The Multigrid Method Is everything really that simple? ? ? 09/09/2020 JASS, 2005, St. Petersburg 3

Testing Ground • One-dimensional boundary value problem describing the steady-state temperature distribution in a long uniform rod • Grid: 09/09/2020 JASS, 2005, St. Petersburg 4

Approximation with the finite difference method 09/09/2020 JASS, 2005, St. Petersburg 5

Matrix Form 09/09/2020 JASS, 2005, St. Petersburg 6

Testing Ground II • Two-dimensional boundary value problem 09/09/2020 JASS, 2005, St. Petersburg 7

Approximation with the finite difference method 09/09/2020 JASS, 2005, St. Petersburg 8

Matrix Form 09/09/2020 JASS, 2005, St. Petersburg 9

Matrix Form II 09/09/2020 JASS, 2005, St. Petersburg 10

Content • • Model Problems Basic Iterative Schemes The Multigrid Method Is everything really that simple? ? ? 09/09/2020 JASS, 2005, St. Petersburg 11

Some Notations and Definitions 09/09/2020 JASS, 2005, St. Petersburg 12

Stationary Linear Iterations 09/09/2020 JASS, 2005, St. Petersburg 13

Assymptotic Convergence Factor 09/09/2020 JASS, 2005, St. Petersburg 14

Jacobi Relaxation 09/09/2020 JASS, 2005, St. Petersburg 15

Gauss-Seidel Relaxation • Components of the new approximation are used as soon as they are calculated – reduced storage requirements 09/09/2020 JASS, 2005, St. Petersburg 16

Fourier Modes 09/09/2020 JASS, 2005, St. Petersburg 17

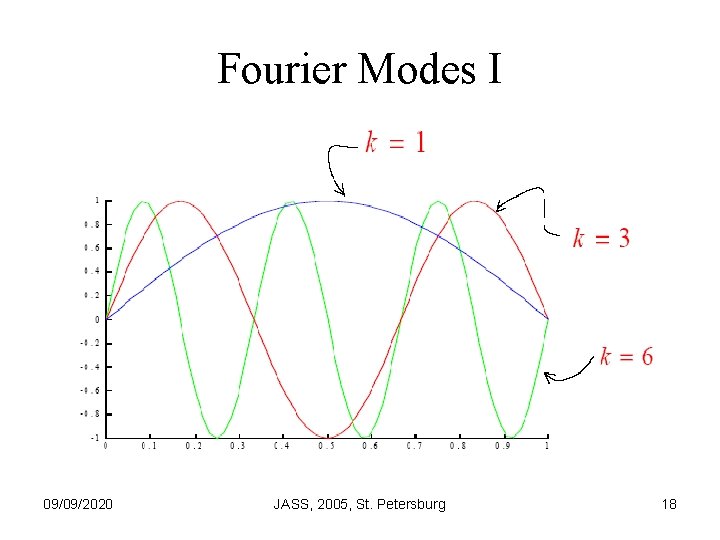
Fourier Modes I 09/09/2020 JASS, 2005, St. Petersburg 18

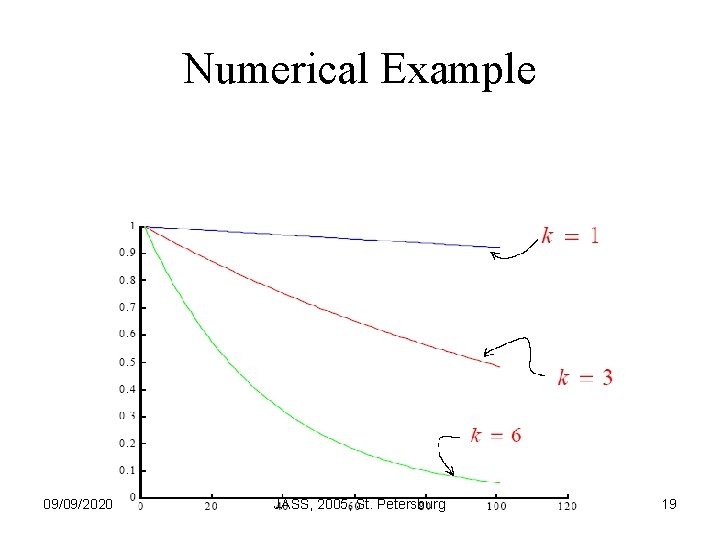
Numerical Example 09/09/2020 JASS, 2005, St. Petersburg 19

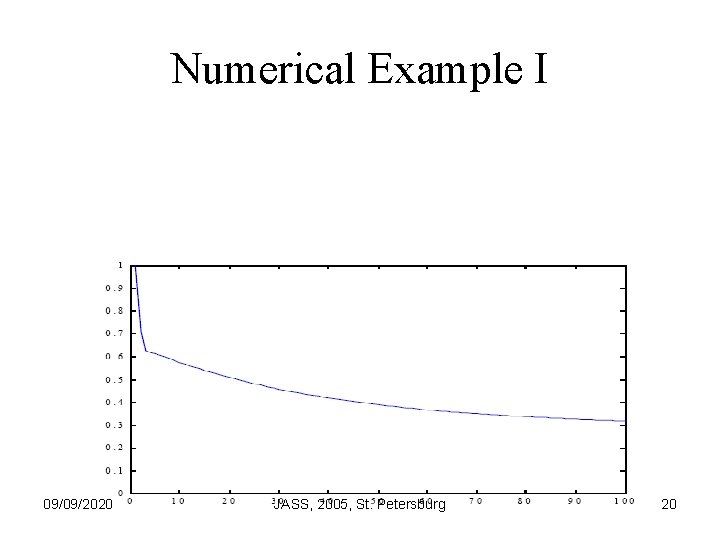
Numerical Example I 09/09/2020 JASS, 2005, St. Petersburg 20

Observation • Standard iterations converge quickly as long as the error has high-frequency components • BUT the slow elimination of the low frequency components of the error degrades the performance 09/09/2020 JASS, 2005, St. Petersburg 21

Why? 09/09/2020 JASS, 2005, St. Petersburg 22

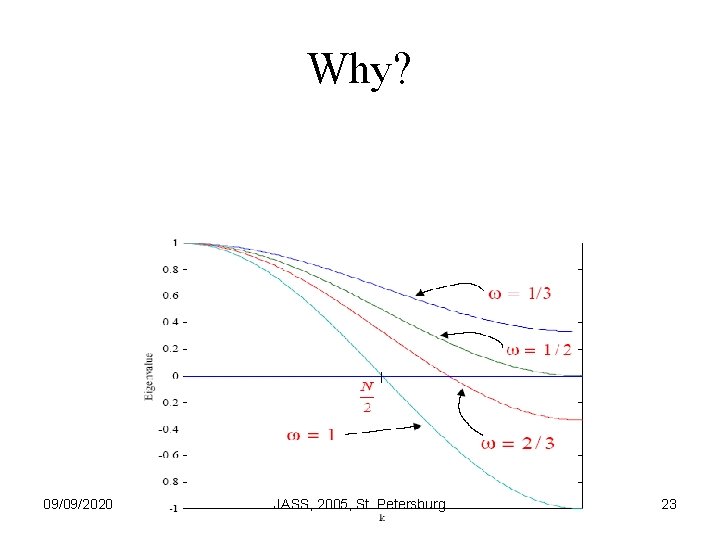
Why? 09/09/2020 JASS, 2005, St. Petersburg 23

Conclusion • The eigenvalue associated with the smoothest mode will always be close to 1 (esspecially for smaller grid spacing) • No value of can reduce the smooth components of the error effectively • What value of damps best the oscillatory components of the error? 09/09/2020 JASS, 2005, St. Petersburg 24

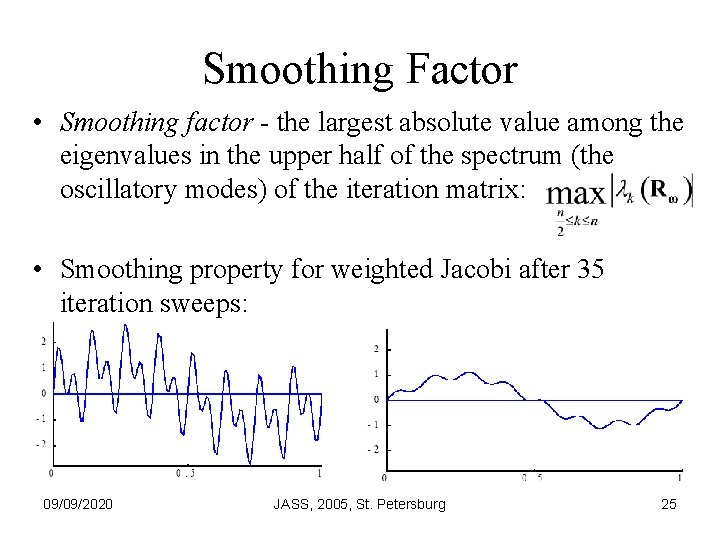
Smoothing Factor • Smoothing factor - the largest absolute value among the eigenvalues in the upper half of the spectrum (the oscillatory modes) of the iteration matrix: • Smoothing property for weighted Jacobi after 35 iteration sweeps: 09/09/2020 JASS, 2005, St. Petersburg 25

Content • • Model Problems Basic Iterative Schemes The Multigrid Method Is everything really that simple? ? ? 09/09/2020 JASS, 2005, St. Petersburg 26

Elements of Multigrid • • Coarse Grids Nested Iteration Correction Scheme Interpolation Operator Restriction Operator Two-Grid Correction Scheme V-Cycle Scheme Full Multigrid V-Cycle - FMG 09/09/2020 JASS, 2005, St. Petersburg 27

Coarse Grids 09/09/2020 JASS, 2005, St. Petersburg 28

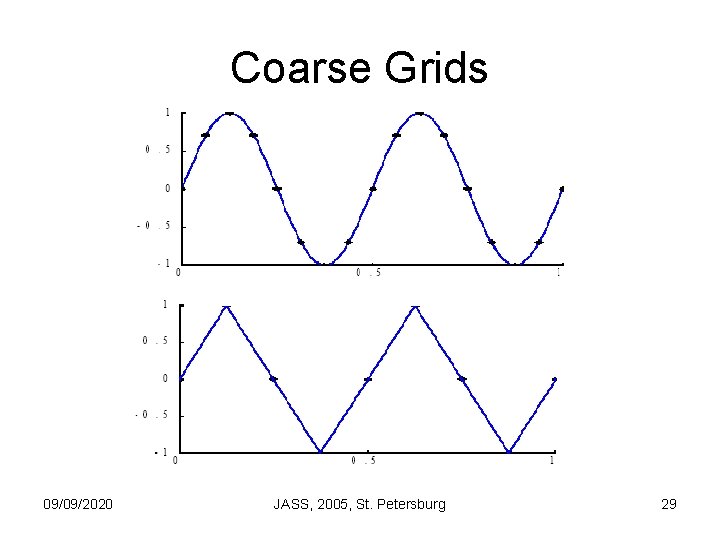
Coarse Grids 09/09/2020 JASS, 2005, St. Petersburg 29

Coarse Grids 09/09/2020 JASS, 2005, St. Petersburg 30

Nested Iteration • Compute an improved initial guess for the fine-grid relaxation 09/09/2020 JASS, 2005, St. Petersburg 31

Correction Scheme 09/09/2020 JASS, 2005, St. Petersburg 32

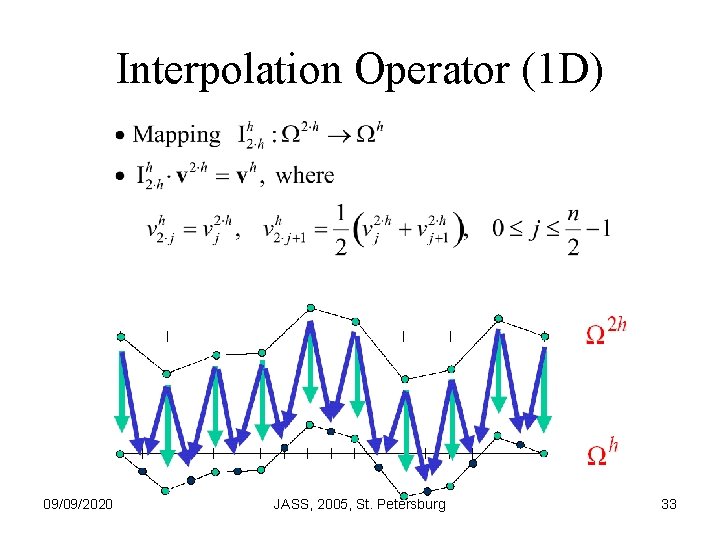
Interpolation Operator (1 D) 09/09/2020 JASS, 2005, St. Petersburg 33

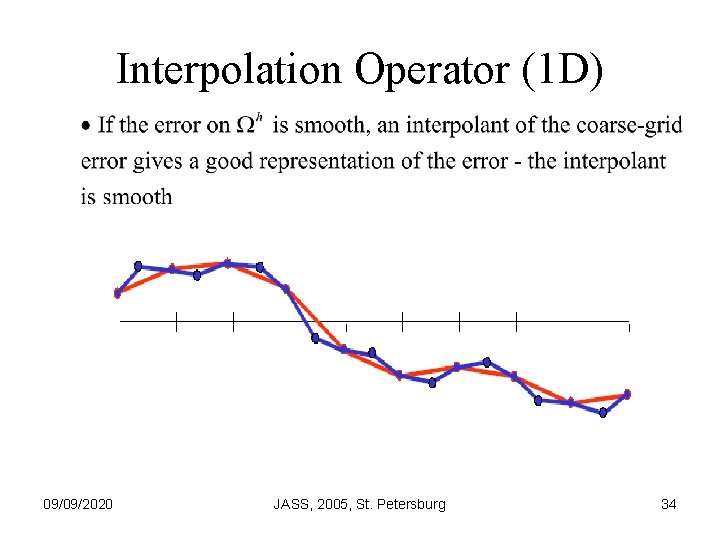
Interpolation Operator (1 D) 09/09/2020 JASS, 2005, St. Petersburg 34

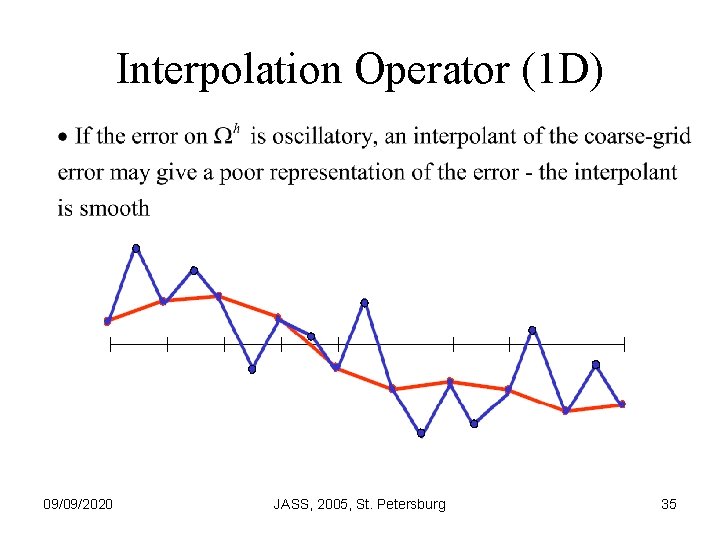
Interpolation Operator (1 D) 09/09/2020 JASS, 2005, St. Petersburg 35

Interpolation Operator (1 D) 09/09/2020 JASS, 2005, St. Petersburg 36

Restriction Operator (1 D) 09/09/2020 JASS, 2005, St. Petersburg 37

Full Weighting 09/09/2020 JASS, 2005, St. Petersburg 38

Two-Grid Correction Scheme 09/09/2020 JASS, 2005, St. Petersburg 39

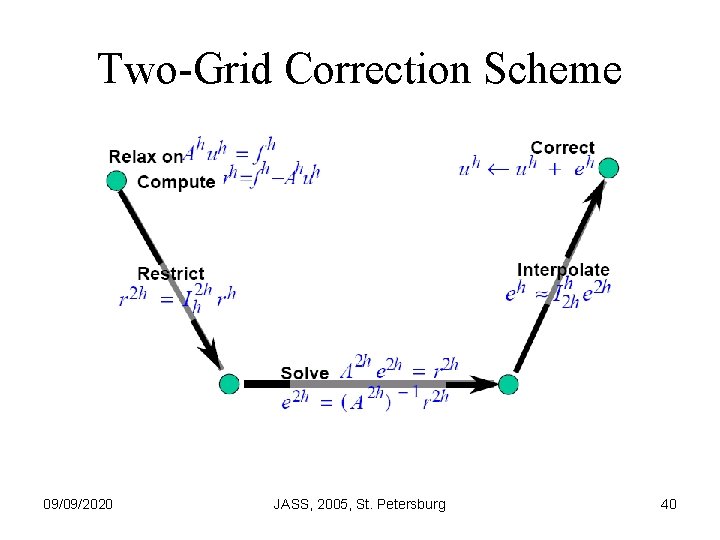
Two-Grid Correction Scheme 09/09/2020 JASS, 2005, St. Petersburg 40

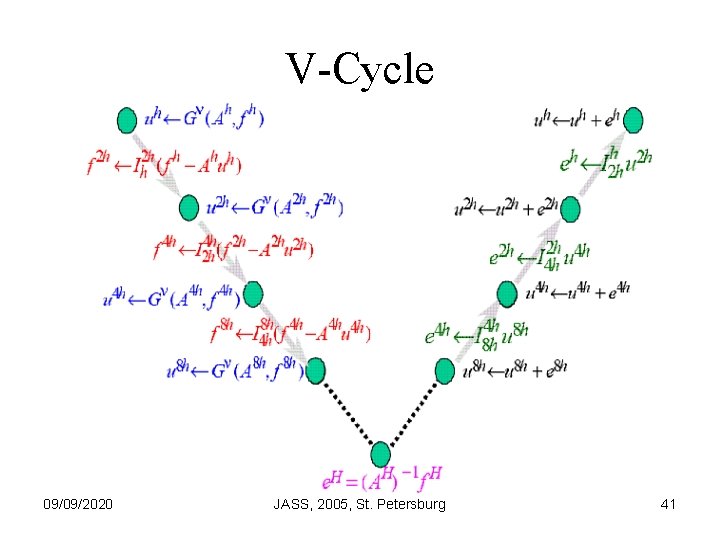
V-Cycle 09/09/2020 JASS, 2005, St. Petersburg 41

V-Cycle - Recursive 09/09/2020 JASS, 2005, St. Petersburg 42

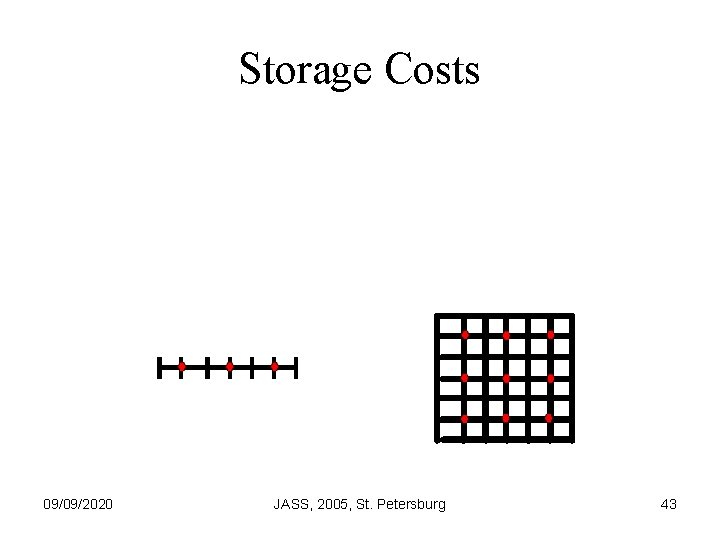
Storage Costs 09/09/2020 JASS, 2005, St. Petersburg 43

Computational Costs 09/09/2020 JASS, 2005, St. Petersburg 44

Convergence Analysis 09/09/2020 JASS, 2005, St. Petersburg 45

Converging to Level of Truncation 09/09/2020 JASS, 2005, St. Petersburg 46

Full Multigrid V-Cycle 09/09/2020 JASS, 2005, St. Petersburg 47

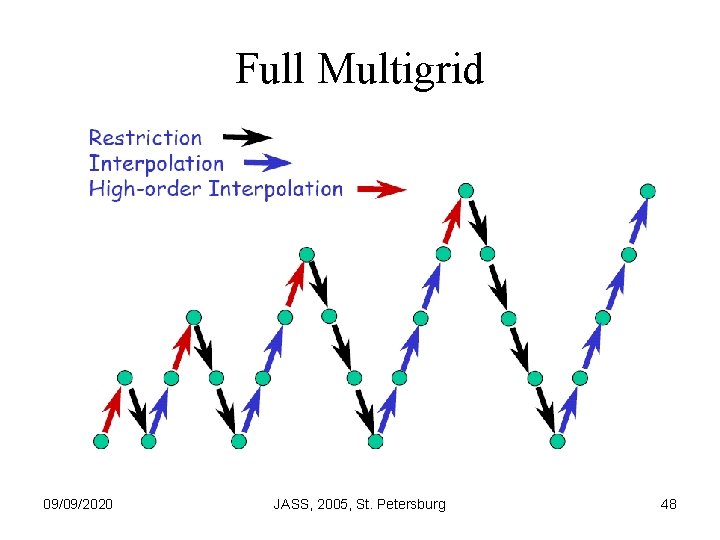
Full Multigrid 09/09/2020 JASS, 2005, St. Petersburg 48

Full Multigrid - Recursive 09/09/2020 JASS, 2005, St. Petersburg 49

Costs of Full Multigrid 09/09/2020 JASS, 2005, St. Petersburg 50

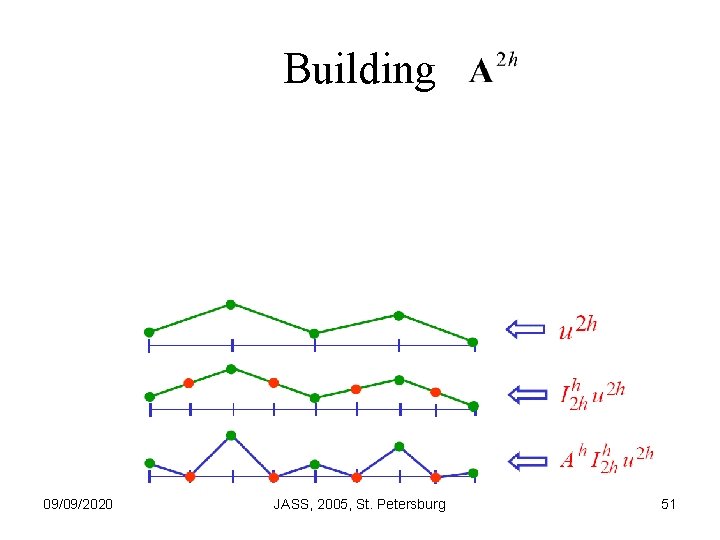
Building 09/09/2020 JASS, 2005, St. Petersburg 51

Variational Properties 09/09/2020 JASS, 2005, St. Petersburg 52

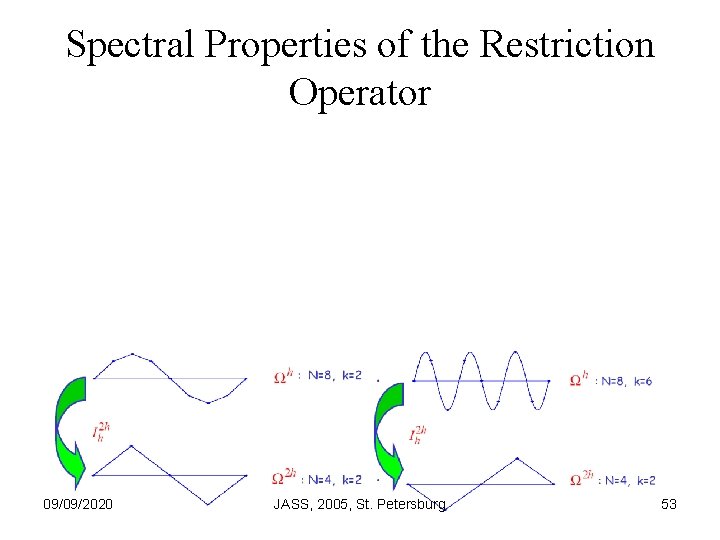
Spectral Properties of the Restriction Operator 09/09/2020 JASS, 2005, St. Petersburg 53

Spectral Properties of the Interpolation Operator 09/09/2020 JASS, 2005, St. Petersburg 54

Two-Grid Correction Scheme 09/09/2020 JASS, 2005, St. Petersburg 55

Algebraic Analysis 09/09/2020 JASS, 2005, St. Petersburg 56

Spectral and Algebraic Decompozition • Spectral decompozition: • Algebraic decompozition: 09/09/2020 JASS, 2005, St. Petersburg 57

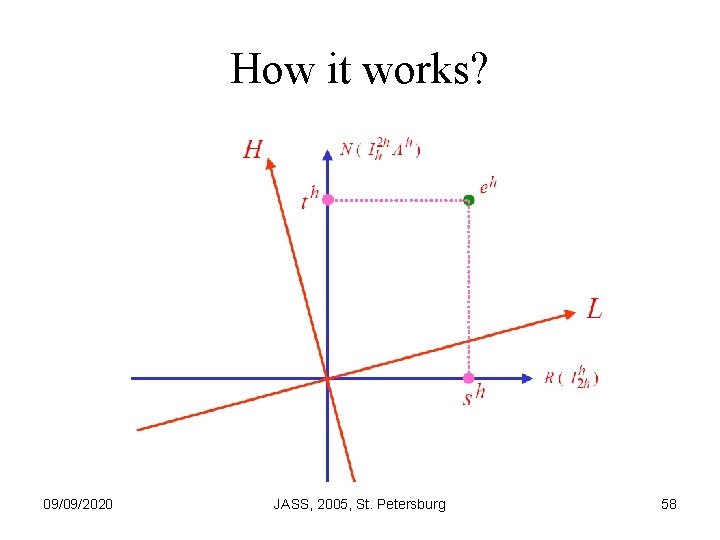
How it works? 09/09/2020 JASS, 2005, St. Petersburg 58

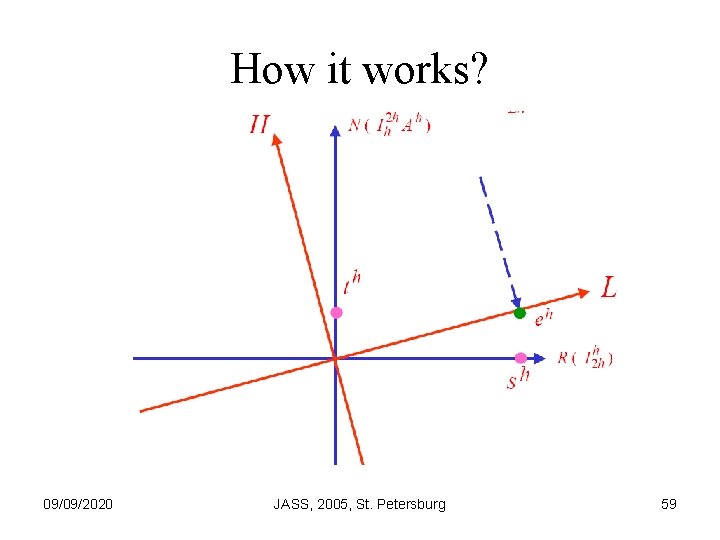
How it works? 09/09/2020 JASS, 2005, St. Petersburg 59

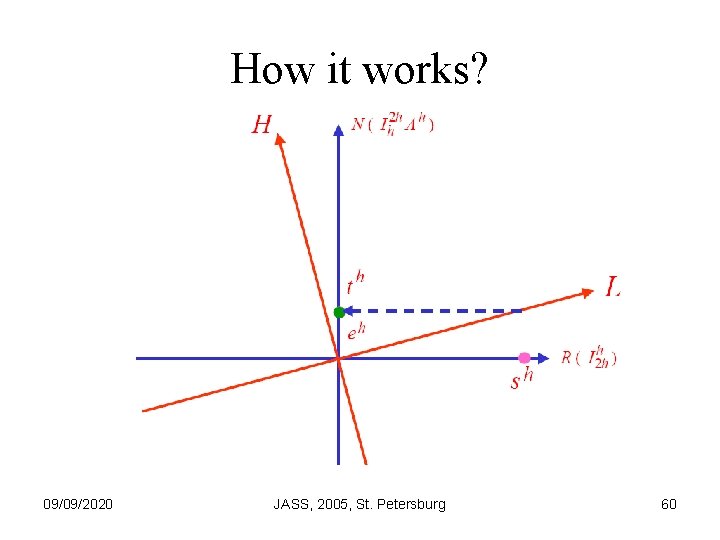
How it works? 09/09/2020 JASS, 2005, St. Petersburg 60

Is everything really so simple? ? ? • • • Anisotropic operators and grids Discontinuous or anisotropic coefficients Nonlinear problems Non-scalar PDE systems High order discretization Algebraic Turbulence models Chemicaly reacting flows Shocks Small-scale singularities 09/09/2020 JASS, 2005, St. Petersburg 61