Introduction to MPI Eric Aubanel Advanced Computational Research

Introduction to MPI Eric Aubanel Advanced Computational Research Laboratory Faculty of Computer Science, UNB Fredericton, New Brunswick

Goals • How to decompose your problem to solve it in parallel? • What patterns of communication arise in solving problems? • What is a minimal subset of commands necessary to do parallel computing? • What is the MPI syntax? – Hello world example • What is collective communication? – Matrix multiply example • How to distribute the work evenly among the processors – Static & dynamic load balancing with fractals

Is Parallelism For You? The nature of the problem is the key contributor to ultimate success or failure in parallel programming

Problem Architectures Type of decomposition dictated by the problem’s architecture • Perfect Parallelism easier – wholly independent calculations • Seismic Imaging, fractals (see later) • Pipeline Parallelism – overlap work that would be done sequentially • simulation followed by image rendering harder • Fully Synchronous Parallelism – future computations or decisions depend on the results of all preceding data calculations • weather forecasting • Loosely Synchronous Parallelism – Processors each do parts of the problem, exchanging information intermittently. • contaminant flow

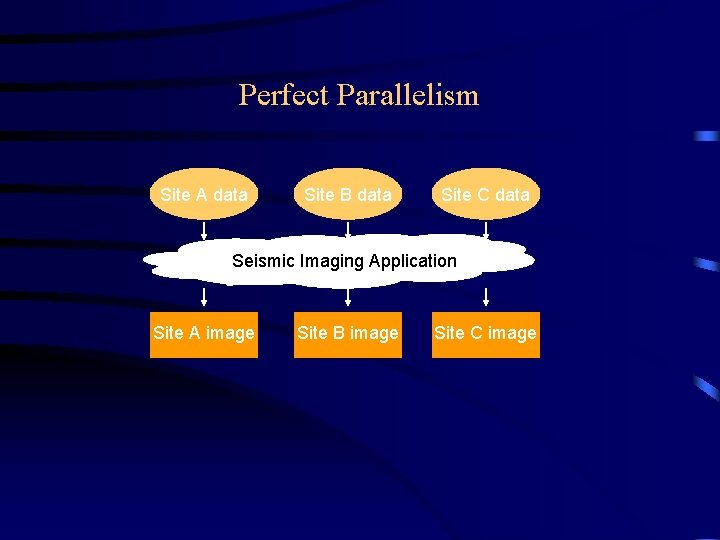
Perfect Parallelism Site A data Site B data Site C data Seismic Imaging Application Site A image Site B image Site C image

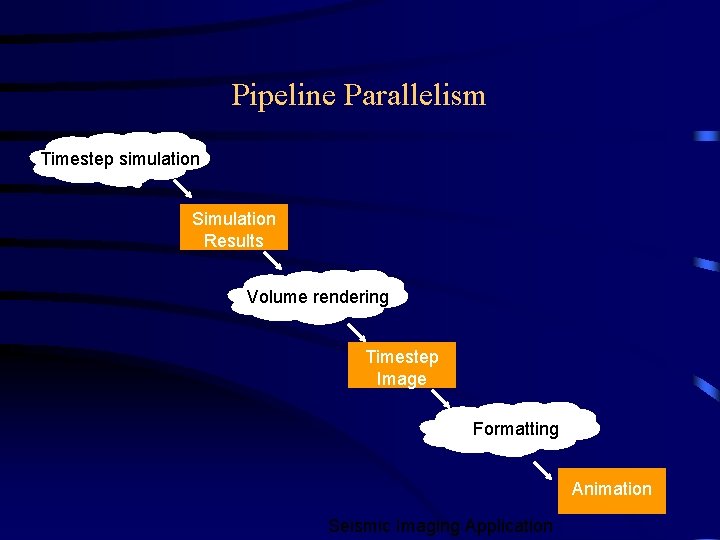
Pipeline Parallelism Timestep simulation Simulation Results Volume rendering Timestep Image Formatting Animation Seismic Imaging Application

Synchronous Parallelism

Three steps to a successful parallel program 1. Choose a decomposition and map to the processors • perfectly parallel, pipeline, etc. • ignore topology of the system interconnect and use the natural topology of the problem 2. Define the inter-process communication protocol • specify the different types of messages which need to be sent • see if standard libraries efficiently support the proposed message patterns. 3. Tune: alter the application to improve performance • balance the load among processors • minimize the communication-to-computation ratio • eliminate or minimize sequential bottlenecks (Is one processor doing all the work while the others wait for some event to happen? ) • minimize synchronization. All processors should work independently where possible. Synchronize only where necessary

Domain Decomposition • In the scientific world (esp. in the world of simulation and modelling) this is the most common solution • The solution space (which often corresponds to real space) is divided up among the processors. Each processor solves its own little piece • Finite-difference methods and finite-element methods lend themselves well to this approach • The method of solution often leads naturally to a set of simultaneous equations that can be solved by parallel matrix solvers

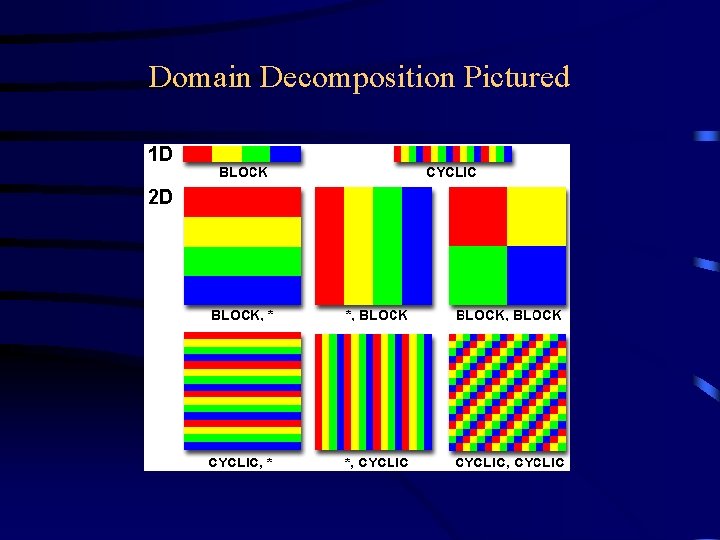
Domain Decomposition Pictured

Finite Element Decomposition • Cover the whole domain with finite elements, then break up the car in various places depending on how many processors you are likely to have • Each subdomain proceeds independently except on the boundaries between processors • Challenging for dynamic codes (e. g. crash simulations) since the shape of the car changes. Elements that were not close together at the beginning may come into close proximity • Decomposition may have to change as the calculation proceeds

Gravitational N-Body Problem Given a box containing N particles that interact with each other only through gravitational attraction, describe the trajectory of the particles as a function of time.

Solution to Gravitational N-Body Problem • Calculate the force and acceleration on each particle • Update each particle’s velocity and position • One parallel solution: spatial decomposition

Spatial Decomposition of N-Body Problem What happens when all the particles start condensing in one of the small boxes?

Particle Decomposition of N-Body Problem

Message Passing Model • We have an ensemble of processors and memory they can access • Each processor executes its own program • All processors are interconnected by a network (or a hierarchy of networks) • Processors communicate by passing messages • Contrast with Open. MP: implicit communication

The Process: basic unit of the application Characteristics of a process: • A running executable of a (compiled and linked) program written in a standard sequential language (e. g. Fortran or C) with library calls to implement the message passing • A process executes on a processor – all processes are assigned to processors in a one-to-one mapping (in the simplest model of parallel programming) – other processes may execute on other processors • A process communicates and synchronizes with other processes via messages.

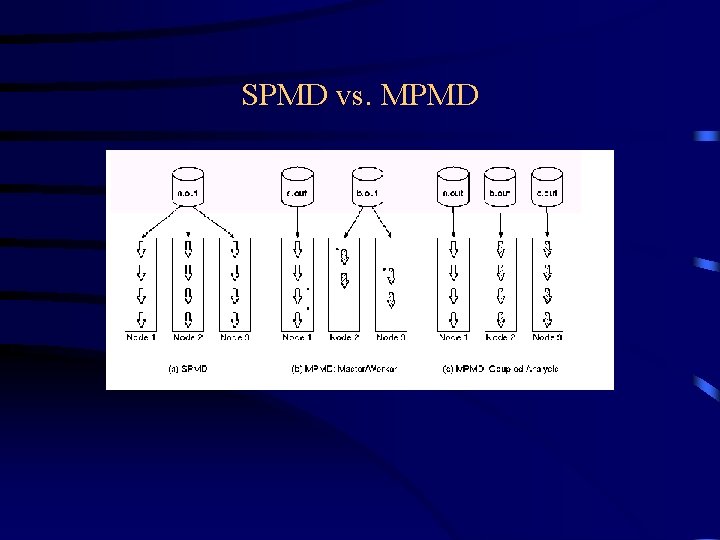
SPMD vs. MPMD

SPMD for performance Not just for MPI: even Open. MP programmers should use SPMD model for high performance, scalable applications

Programmer’s View of the Application The characteristics of the problem and the way it has been implemented in code affect the process structure of an application

Characteristics of the Programming Model • Computations are performed by a set of parallel processes • Data accessed by one process is private from all other processes – memory and variables are not shared. • When sharing of data is required, processes send messages to each other

Message Passing Interface • MPI 1. 0 standard in 1994 • MPI 1. 1 in 1995 • MPI 2. 0 in 1997 – Includes 1. 1 but adds new features • MPI-IO • One-sided communication • Dynamic processes

Advantages of MPI • Universality • Expressivity – Well suited to formulating a parallel algorithm • Ease of debugging – Memory is local • Performance – Explicit association of data with process allows good use of cache

Disadvantages of MPI • Harder to learn than shared memory programming (Open. MP) • Does not allow incremental parallelization: all or nothing!

MPI Functionality • Several modes of point-to-point message passing – – blocking (e. g. MPI_SEND) non-blocking (e. g. MPI_ISEND) synchronous (e. g. MPI_SSEND) buffered (e. g. MPI_BSEND) • Collective communication and synchronization – e. g. MPI_BCAST, MPI_BARRIER • User-defined datatypes • Logically distinct communicator spaces • Application-level or virtual topologies

What System Calls Enable Parallel Computing? A simple subset: • send: send a message to another process • receive: receive a message from another process • size_the_system: how many processes am I using to run this code • who_am_i: What is my process number within the parallel application

Message Passing Model • Processes communicate and synchronize with each other by sending and receiving messages – no global variables and no shared memory • All remote memory references must be explicitly coordinated with the process that controls the memory location being referenced. – two-sided communication • Processes execute independently and asynchronously – no global synchronizing clock • Processes may be unique and work on own data set – supports MIMD processing • Any process may communicate with any other process – there are no a priori limitations on message passing. However, although one process can talk, the other is not required to listen!

Starting and Stopping MPI • Every MPI code needs to have the following form: program my_mpi_application include ‘mpif. h’. . . call mpi_init (ierror) /* ierror is where mpi_init puts the error code describing the success or failure of the subroutine call. */. . . < the program goes here!>. . . call mpi_finalize (ierror) /* Again, make sure ierror is present! */ stop end • Although, strictly speaking, executable statements can come before MPI_INIT and after MPI_FINALIZE, they should have nothing to do with MPI. • Best practice is to bracket your code completely by these statements.

Finding out about the application How many processors are in the application? call MPI_COMM_SIZE ( comm, num_procs ) • returns the number of processors in the communicator. • if comm = MPI_COMM_WORLD, the number of processors in the application is returned in num_procs. Who am I? call MPI_COMM_RANK ( comm, my_id ) • returns the rank of the calling process in the communicator. • if comm = MPI_COMM_WORLD, the identity of the calling process is returned in my_id. • my_id will be a whole number between 0 and the num_procs - 1.

Timing • When analysing performance, it is often useful to get timing information about how sections of the code are performing. • MPI_WTIME () – returns a double-precision number that represents the number of seconds from some fixed point in the past. – That fixed point will stay fixed for the duration of the application, but will change from run to run. – MPI assumes no synchronization between processes. – Every processor will return its own value on a call to MPI_WTIME. – can be inefficient

MPI_WTIME • The importance of MPI_WTIME is in timing segments of code running on a given processor: start_time = MPI_WTIME () do (a lot of work) elapsed_time = MPI_WTIME() - start_time • It is wall-clock time, so if a process sits idle, time still accumulates.

Basis Set of MPI Message-Passing Subroutines MPI_SEND (buf, count, datatype, dest, tag, comm, ierror) • send a message to another process in this MPI application MPI_RECV (buf, count, datatype, source, tag, comm, status, ierror) • receive a message from another process in this MPI application MPI_COMM_SIZE (comm, numprocs, ierror) • total number of processes allocated to this MPI application MPI_COMM_RANK (comm, myid, ierror) • logical process number of this (the calling) process within this MPI application

MPI in Fortran and C Important Fortran and C difference: • In Fortran the MPI library is implemented as a collection of subroutines. • In C, it is a collection of functions. • In Fortran, any error return code must appear as the last argument of the subroutine. • In C, the error code is the value the function returns.

MPI supports several forms of SENDs and RECVs Which form of the send and receive is best is problem dependent Here are the different types: • Complete (aka blocking): MPI_SEND, MPI_RECV • Incomplete (aka non-blocking or asynchronous): MPI_ISEND, MPI_IRECV • Combined: MPI_SENDRECV • Buffered: MPI_BSEND • Fully synchronous: MPI_SSEND and there are more! We will focus on the simplest MPI_SEND and MPI_RECV.

MPI Datatypes MPI defines its own datatypes • important for heterogeneous applications • implemented so that the MPI datatype is the same as the corresponding elementary datatype on the host machine – e. g. MPI_REAL is a four-byte floating-point number on an IBM SP is an eight-byte floating-point number on a Cray T 90. • designed so that if one system sends 100 MPI_REALs to a system having a different architecture, the receiving system will still receive 100 MPI_REALs in its native format

Elementary MPI Datatypes - Fortran MPI Datatype Fortran Datatype MPI_BYTE MPI_CHARACTER MPI_COMPLEX MPI_DOUBLE_PRECISION DOUBLE PRECISION (REAL*8) MPI_INTEGER MPI_LOGICAL MPI_PACKED MPI_REAL (REAL*4)

Elementary MPI Datatypes - C MPI Datatype MPI_BYTE MPI_CHAR MPI_DOUBLE MPI_FLOAT MPI_INT MPI_LONG_LONG_INT MPI_LONG_DOUBLE MPI_PACKED MPI_SHORT MPI_UNSIGNED_CHAR MPI_UNSIGNED_LONG MPI_UNSIGNED_SHORT C Datatype signed char double float int long double short unsigned char unsigned int unsigned long unsigned short

Simple MPI Example My_Id, numb_of_ procs 0, 3 This is from MPI process number 0 1, 3 This is from MPI processes other than 0 2, 3 This is from MPI processes other than 0

Simple MPI Example Program Trivial implicit none include "mpif. h" ! MPI header file integer My_Id, Numb_of_Procs, Ierr call MPI_INIT ( ierr ) call MPI_COMM_RANK ( MPI_COMM_WORLD, My_Id, ierr ) call MPI_COMM_SIZE ( MPI_COMM_WORLD, Numb_of_Procs, ierr ) print *, ' My_id, numb_of_procs = ', My_Id, Numb_of_Procs if ( My_Id. eq. 0 ) then print *, ' This is from MPI process number ', My_Id else print *, ' This is from MPI processes other than 0 ', My_Id end if call MPI_FINALIZE ( ierr ) ! bad things happen if you forget ierr stop end

Simple MPI C Example #include <stdio. h> #include <mpi. h> int main(int argc, char * argv[]) { int taskid, ntasks; MPI_Init(&argc, &argv); MPI_Comm_rank(MPI_COMM_WORLD, &taskid); MPI_Comm_size(MPI_COMM_WORLD, &ntasks); printf("Hello from task %d. n", taskid); MPI_Finalize(); return(0); }

Matrix Multiply Example A B X C =

Matrix Multiply Example Intialize matrices A & B time 1=timef()/1000 call jikloop time 2=timef()/1000 print *, time 2 -time 1 subroutine jikloop integer : : matdim, ncols real(8), dimension (: , : ) : : a, b, c real(8) : : cc do j = 1, matdim do i = 1, matdim cc = 0. 0 d 0 do k = 1, matdim cc = cc + a(i, k)*b(k, j) end do c(i, j) = cc end do end subroutine jikloop

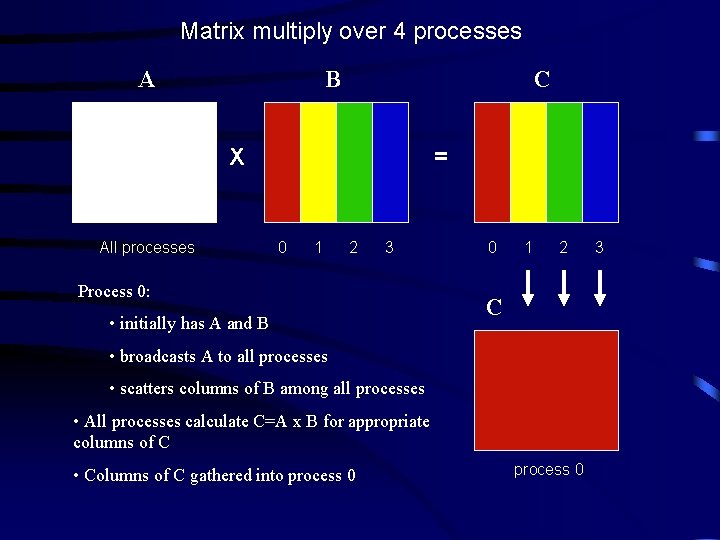
Matrix multiply over 4 processes A B C X All processes = 0 1 2 3 Process 0: • initially has A and B 0 1 2 C • broadcasts A to all processes • scatters columns of B among all processes • All processes calculate C=A x B for appropriate columns of C • Columns of C gathered into process 0 3

MPI Matrix Multiply real a(dim, dim), b(dim, dim), c(dim, dim) ncols = dim/numprocs if( myid. eq. master ) then ! Intialize matrices A & B time 1=timef()/1000 call Broadcast(a to all) do i=1, numprocs-1 call Send(ncols columns of b to i) end do call jikloop ! c(1 st ncols) = a x b(1 st ncols) do i=1, numprocs-1 call Receive(ncols columns of c from i) end do time 2=timef()/1000 print *, time 2 -time 1 else ! Processors other than master allocate ( blocal(dim, ncols), clocal(dim, ncols) ) call Broadcast(a to all) call Receive(blocal from master) call jikloop ! clocal=a*blocal call Send(clocal to master) endif

MPI Send call Send(ncols columns of b to i): call MPI_SEND( b(1, i*ncols+1), ncols*matdim, & MPI_DOUBLE_PRECISION, i, tag & MPI_COMM_WORLD, ierr ) • b(1, i*ncols+1 ): address where the data start. • ncols*matdim : The number of elements (items) of data in the message • MPI_DOUBLE_PRECISION: type of data to be transmitted • i: message is sent to process i • tag: message tag, an integer to help distinguish among messages

MPI Receive call Receive(ncols columns of c from i) : call MPI_RECV( c(1, i*ncols+1), ncols*matdim, & MPI_DOUBLE_PRECISION, i, tag & MPI_COMM_WORLD, status, ierr) • status: integer array of size MPI_STATUS_SIZE of information that is returned. For example, if you specify a wildcard (MPI_ANY_SOUCE or MPI_ANY_TAG) for source or tag, status will tell you the actual rank (status(MPI_SOURCE)) or tag (status(MPI_TAG)) for the message received.

Collective Communications • allows many nodes to communicate with each other • MPI defines subroutines/functions that implement common collective modes of communication. • relieves the user of having to develop his/her own out of send/recv primitives. • Good MPI implementations should have these collective operations already optimized for the target hardware.

Some Fundamental Modes of Collective Communication • broadcast • reduce • barrier • scatter • gather Send something from one processor to everybody Send something from everybody and combine it together on one processor Pause until everybody has encountered this barrier Take multiple pieces of data from one process and send individual pieces of it to individual processes Gather individual pieces of data from individual processes and create multiple pieces of data on a single process.

The Broadcast Operation: MPI_BCAST Useful when one processor has data that is needed by everyone.

Using MPI_BCAST Processor 0 Processors 1, 2, 3, . . . , n pi = 3. 14159 pi = uninitialized pi = 3. 14159 MPI_BCAST pi = uninitialized MPI_BCAST C This runs on processor 0. real*8 pi integer ierr if (my_rank. eq. 0) pi = 3. 14159 call mpi_bcast(pi, 1, MPI_DOUBLE_PRECISION, 0, MPI_COMM_WORLD, ierr) pi = 3. 14159 C This runs on processor 1, 2, 3, . . . , n C It's the same code that runs on proc 0! real*8 pi integer ierr if (my_rank. eq. 0) pi = 3. 14159 call mpi_bcast(pi, 1, MPI_DOUBLE_PRECISION, 0, MPI_COMM_WORLD, ierr)

MPI Broadcast call Broadcast(a to all): call MPI_BCAST( a, matdimsq, MPI_DOUBLE_PRECISION, master, MPI_COMM_WORLD, ierr ) • master: message is broadcast from master process (myid=0)

Better MPI Matrix Multiply if( myid. eq. master ) then ! Intialize matrices A & B time 1=timef()/1000 endif call Broadcast ( a, enveloppe) call Scatter (b, blocal, enveloppe) call jikloop ! clocal = a * blocal call Gather (clocal, c, enveloppe) if( myid. eq. Master) then time 2=timef()/1000 print *, time 2 -time 1 endif

MPI_SCATTER The diagram is a little deceptive. Why?

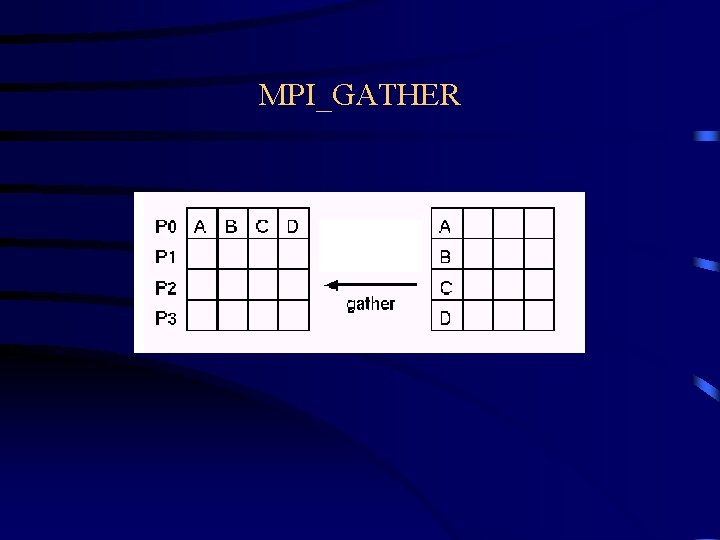
MPI_GATHER

MPI Scatter 100 100 blocal All processes 100 b 100 Master call MPI_SCATTER( b, 100, MPI_DOUBLE_PRECISION, & blocal, 100, MPI_DOUBLE_PRECISION, master, & MPI_COMM_WORLD, ierr)

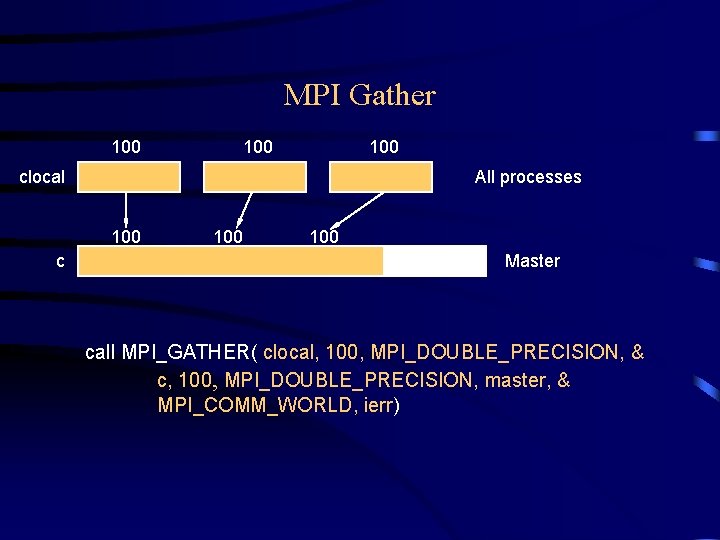
MPI Gather 100 100 clocal All processes 100 c 100 Master call MPI_GATHER( clocal, 100, MPI_DOUBLE_PRECISION, & c, 100, MPI_DOUBLE_PRECISION, master, & MPI_COMM_WORLD, ierr)

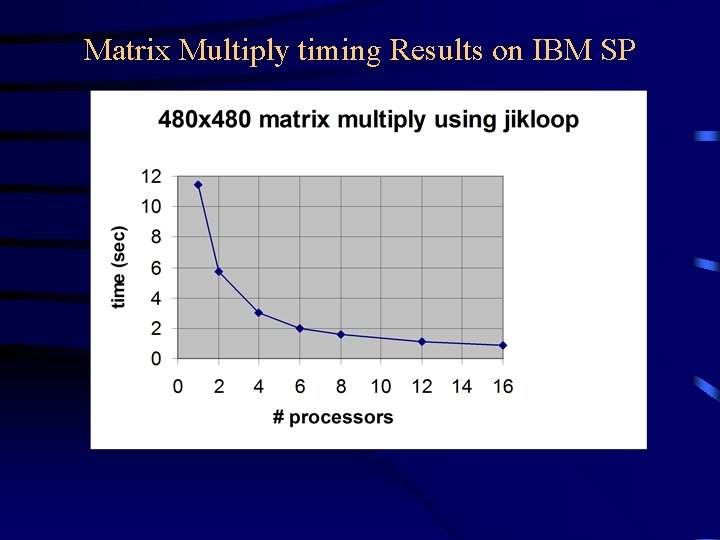
Matrix Multiply timing Results on IBM SP

Measuring Performance Assume we time only parallelized region: Ideally

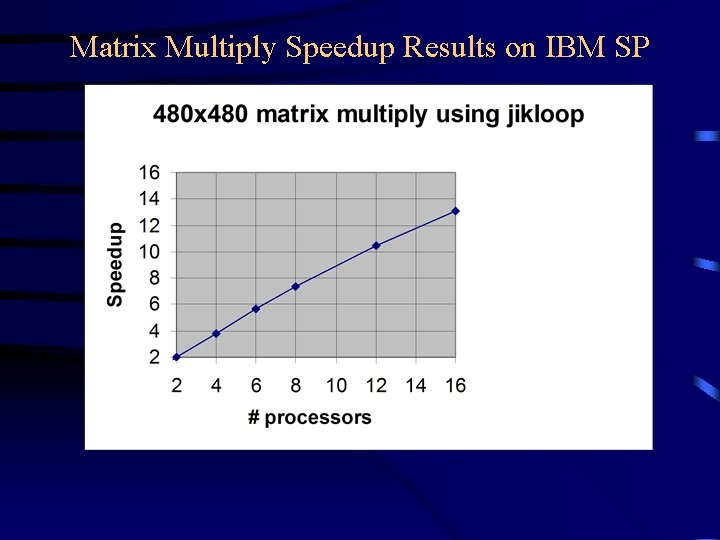
Matrix Multiply Speedup Results on IBM SP

A Closer look at MPI Send/Recv MPI_SEND • MPI_SEND returns after the user send buffer has been copied by the system. • After MPI_SEND returns, the user is free to change the contents of the buffer without affecting the message being sent (i. e. it is guaranteed to already be in some stage of its journey -- and can't be recalled!) • MPI_SEND blocks until the system is finished copying the user buffer. MPI_RECV • MPI_RECV returns after the message has been received and has been copied into the user buffer at the destination. • MPI_RECV blocks until this happened.

What Will Happen? /* Processor 0 */. . . MPI_Send(sendbuf, bufsize, MPI_CHAR, partner, tag, MPI_COMM_WORLD); printf("Posting receive now. . . n"); MPI_Recv(recvbuf, bufsize, MPI_CHAR, partner, tag, MPI_COMM_WORLD, status); /* Processor 1 */. . . MPI_Send(sendbuf, bufsize, MPI_CHAR, partner, tag, MPI_COMM_WORLD); printf("Posting receive now. . . n"); MPI_Recv(recvbuf, bufsize, MPI_CHAR, partner, tag, MPI_COMM_WORLD, status);

Deadlock? #include <stdio. h> #include <mpi. h> #define DIM 2000 int main(int argc, char *argv[]) { int i, taskid, otherid, ntasks; float a[DIM], b[DIM]; MPI_Status status; MPI_Init(&argc, &argv); MPI_Comm_rank(MPI_COMM_WORLD, &taskid); MPI_Comm_size(MPI_COMM_WORLD, &ntasks); for(i=0; i<DIM; i++) a[i]=taskid; otherid=(taskid+1)%2; MPI_Send( &a, DIM, MPI_REAL, otherid, taskid, MPI_COMM_WORLD); MPI_Recv( &b, DIM, MPI_REAL, otherid, MPI_COMM_WORLD, &status); printf("Process %d received array from process %d. n", taskid, otherid); MPI_Finalize(); return(0); }

No Deadlock #include <stdio. h> #include <mpi. h> #define DIM 2000 int main(int argc, char *argv[]) { int i, taskid, otherid, ntasks; float a[DIM], b[DIM]; MPI_Status status; MPI_Request request; MPI_Init(&argc, &argv); MPI_Comm_rank(MPI_COMM_WORLD, &taskid); MPI_Comm_size(MPI_COMM_WORLD, &ntasks); for(i=0; i<DIM; i++) a[i]=taskid; otherid=(taskid+1)%2; MPI_Isend( &a, DIM, MPI_REAL, otherid, taskid, MPI_COMM_WORLD, &request); MPI_Recv( &b, DIM, MPI_REAL, otherid, MPI_COMM_WORLD, &status); printf("Process %d received array from process %d. n", taskid, otherid); MPI_Finalize(); return(0); }

MPI_ISEND call MPI_ISEND ( buf, count, datatype, dest, tag, comm, request, ierror) • request is a handle returned by the subroutines so that MPI_WAIT knows what to wait for – type integer in Fortran and MPI_REQUEST in C • MPI_ISEND returns immediately. • send buffer can be reused once MPI_WAIT returns • unlike, MPI_WAIT, the subroutine MPI_TEST is nonblocking and can be used to determine (repeatedly, if desired) whether the send completed.

Use of non-blocking communication • Where possible, use MPI's features to help overlap computation and communication. • don't wait for a message if there is something else useful to do! • it is always possible to improve performance by overlapping computation and the waiting for a message

= -6 (detail)

imag(c) • = 2 gives mandelbrot set • Colours represent points c in the complex plane, and are mapped to the number of iterations required to diverge • Points that don't diverge are black real(c)

Fractal Example do i=0, pic-1 cx=ax*i+xmin do j=0, pic-1 cy=ymax-ax*j c=dcmplx(cx, cy) ! Initialize z to (0, 0) or (1, 1) do k=1, niter if(abs(z). lt. lim) then ! Z hasn’t diverged yet z=z**alpha+c kount(j, i)=k else exit endif end do

Master-Slave Parallelization: static balancing Slave 1 Slave 2 Slave 3

MPI Fractal: static balancing lblock=pic/(numprocs-1) allocate( kount(0: pic-1, 0: lblock) ) if( myid. eq. master ) then read(*, *) alpha time 1=timef()/1000 call Broadcast(alpha to all) do i=1, numprocs-1 call Receive(kount from i) print *, kount end do time 2=timef()/1000 print *, time 2 -time 1 else ! slaves call Broadcast(alpha to all) call DECOMP_SLAVE(ia, ib) do i=ia, ib …. . kount(j, i-ia)=k …. . end do call Send(kount to master) endif

Master-Slave Parallelization: dynamic balancing

MPI Fractal: dynamic balancing nb=40 allocate( kount(0: pic-1, 0: nb-1), kountal(0: pic-1, 0: pic-1) ) if( myid. eq. master ) then read(*, *) alpha; time 1=timef()/1000 call Broadcast(alpha to all) blocks_done=0; nblocks=pic/nb col_start=(numprocs-1)*nb-nb+1 do while (blocks_done. lt. nblocks) call Receive(kount, any slave) islave=source_of_message call Store_kount_in_kountall blocks_done= blocks_done +1 col_start=col_start+nb call Send(col_start to islave) end do time 2=timef()/1000 print *, time 2 -time 1 else ! slaves call Broadcast(alpha to all) col_start=nb*myid-nb+1 cols_last=pic-nb+1 do while (col_start. le. cols_last) do i=0, nb-1 cx=ax*(i+col_start-1)+xmin …. . Calculate fractal end do call Send(kount to master) call Receive(col_start from master) end do endif

Dynamic Balancing: Detail Master: do while (numdone. lt. nbsize) call MPI_RECV(kount, lkount, MPI_INTEGER, MPI_ANY_SOURCE, & MPI_ANY_TAG, MPI_COMM_WORLD, status, ierr) ncolumn=status(MPI_TAG)-1 islave=status(MPI_SOURCE) Slaves: call MPI_SEND(kount, lkount, MPI_INTEGER, master, col_start, & MPI_COMM_WORLD, ierr)

Common Errors and Misconceptions 1. Forgetting ierr in Fortran (compiler won't always catch this for you) – especially MPI_FINALIZE(ierr) 2. Misdeclaring status in Fortran (must be an array of integers of size MPI_STATUS_SIZE) 3. (For C programmers) Expecting argv and argc to be propagated to all processes. – May or may not happen on all MPI implementations 4. Doing things before MPI_INIT or after MPI_FINALIZE. 5. Matching MPI_BCAST with MPI_Recv

Conclusions Some general principles for good parallel performance: • Balance the computational load • Make the program scalable so that adding nodes makes the program run faster in a predictable way – Parallelize the whole problem • How a problem is decomposed up for parallel execution should depend on the nature of the problem, not the nature of the computer on which it is running • Choice of decomposition determines success of your effort • As in single-processor applications, tuning can yield significant performance gains – Don’t forget single-processor optimization!

Amdahl’s law revisited Horoi & Enbody, J. HPC Applications, 15, no. 1 (2001), p. 75

References • Is Parallelism for You? , by Sheri Pancake, Computational Science and Engineering, Vol. 3, No. 2 (Summer, 1996), pp. 18 -37 • Using MPI, by Gropp, Lusk, and Skjellum (MIT) • Using MPI-2, by same • MPI Website: www-unix. mcs. anl. gov/mpi/ • Matrix multiply programs: www. cs. unb. ca/acrl_workshop/ • Parallel programming with generalized fractals: www. cs. unb. ca/staff/aubanel_fractals. html