Introduction to Morphological Operators About this lecture In

Introduction to Morphological Operators

About this lecture • In this lecture we introduce INFORMALLY the most important operations based on morphology, just to give you the intuitive feeling. • In next lectures we will introduce more formalism and more examples.

Binary Morphological Processing • Non-linear image processing technique – Order of sequence of operations is important • Linear: (3+2)*3 = (5)*3=15 3*3+2*3=9+6=15 • Non-linear: (3+2)2 + (5)2 =25 [sum, then square] (3)2 + (2)2 =9+4=13 [square, then sum] • Based on geometric structure • Used for edge detection, noise removal and feature extraction Used to ‘understand’ the shape/form of a binary image

Introduction • • Structuring Element Erosion Dilation Opening Closing Hit-and-miss Thinning Thickening

1 D Morphological Operations

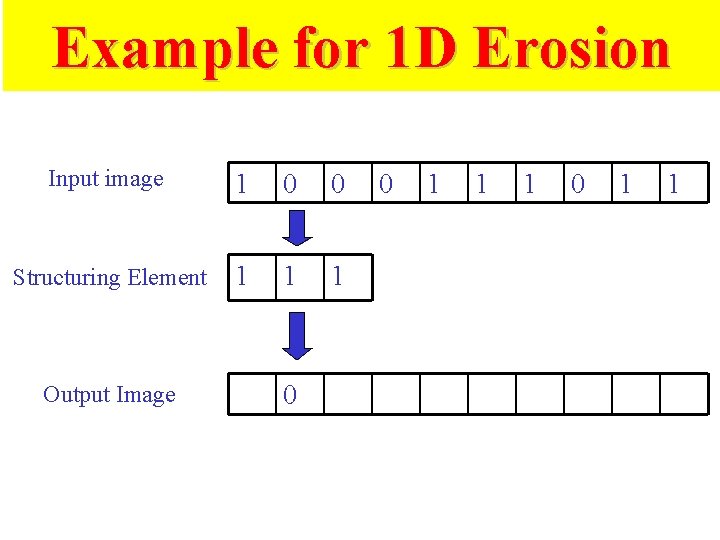
Example for 1 D Erosion Input image 1 0 0 Structuring Element 1 1 1 Output Image 0 0 1 1 1 0 1 1

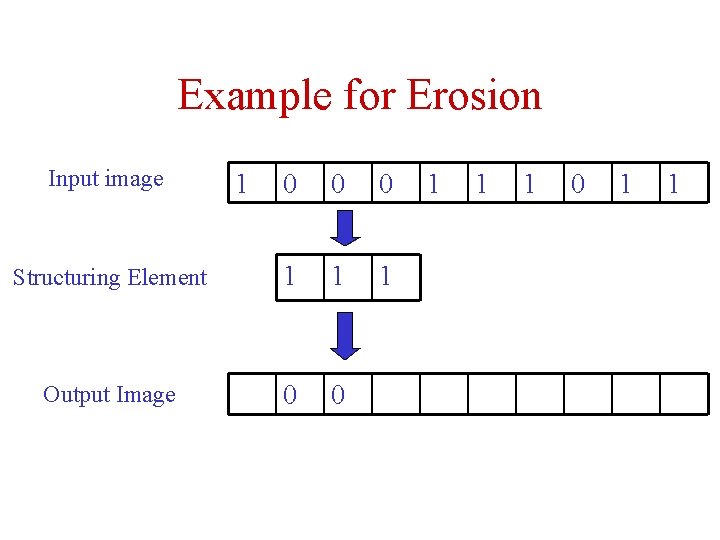
Example for Erosion Input image 1 0 0 0 Structuring Element 1 1 1 Output Image 0 0 1 1 1 0 1 1

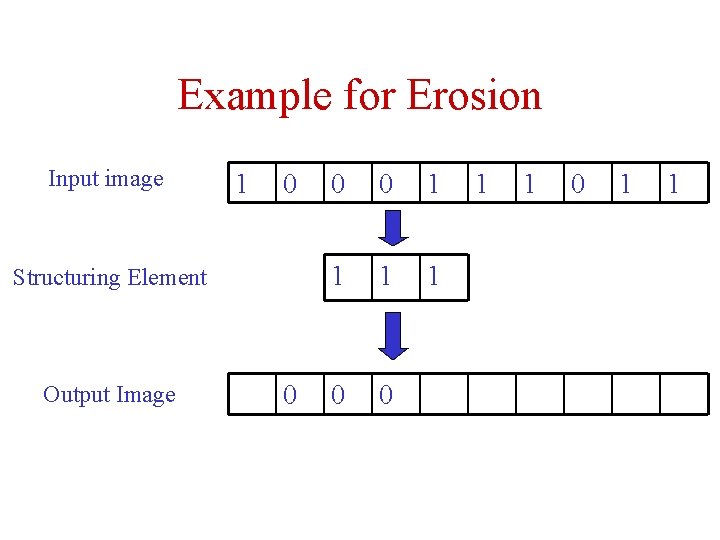
Example for Erosion Input image 1 0 Structuring Element Output Image 0 0 0 1 1

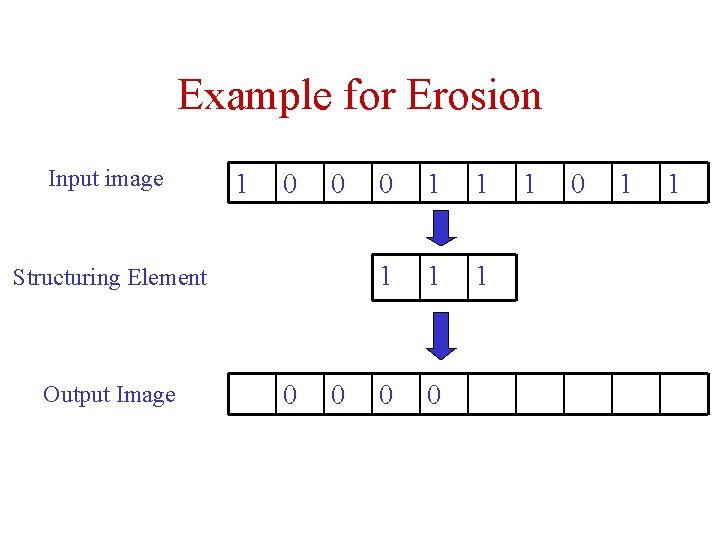
Example for Erosion Input image 1 0 0 Structuring Element Output Image 0 0 0 1 1 1 0 0 1 1

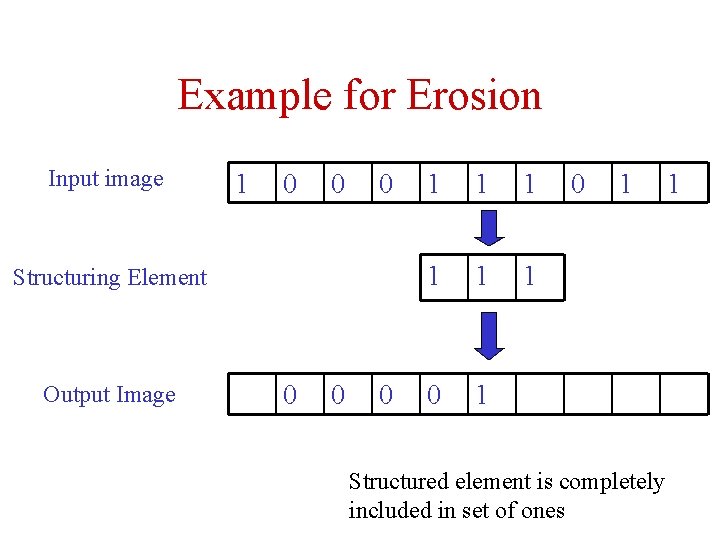
Example for Erosion Input image 1 0 0 0 Structuring Element Output Image 0 0 0 1 1 1 0 1 Structured element is completely included in set of ones 1

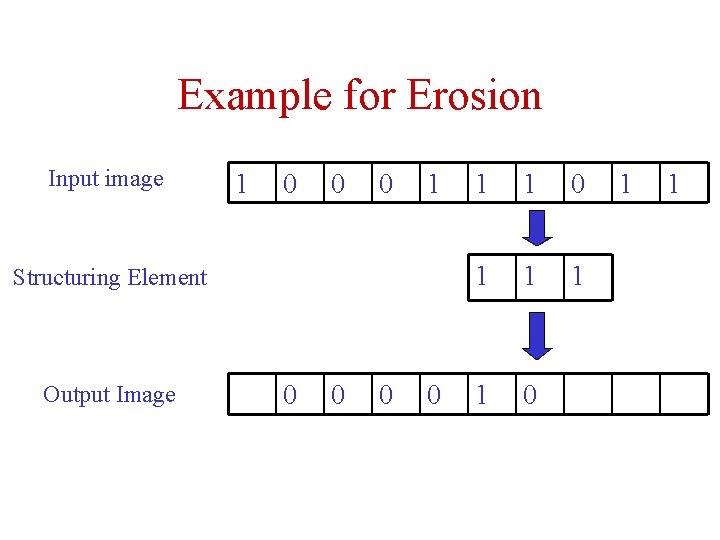
Example for Erosion Input image 1 0 0 0 1 Structuring Element Output Image 0 0 1 1

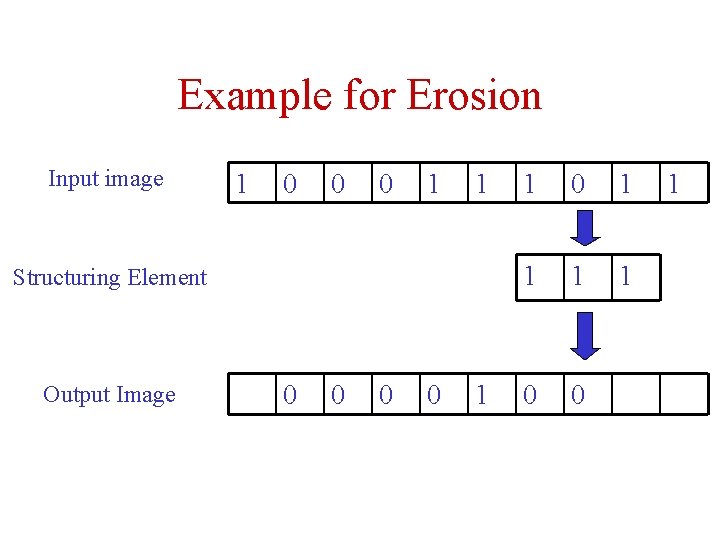
Example for Erosion Input image 1 0 0 0 1 1 Structuring Element Output Image 0 0 1 1 0 0 1

Example for Erosion Input image 1 0 0 0 1 1 1 Structuring Element Output Image 0 0 1 1 1 0 0

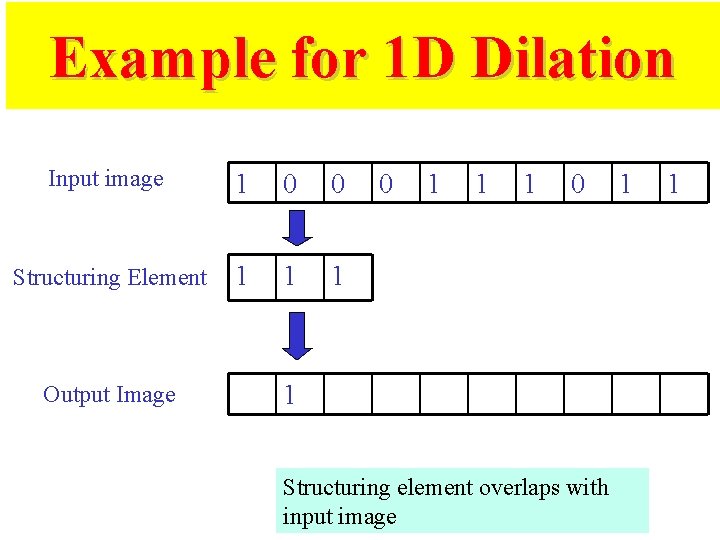
Example for 1 D Dilation Input image 1 0 0 Structuring Element 1 1 1 Output Image 0 1 1 1 0 1 Structuring element overlaps with input image 1 1

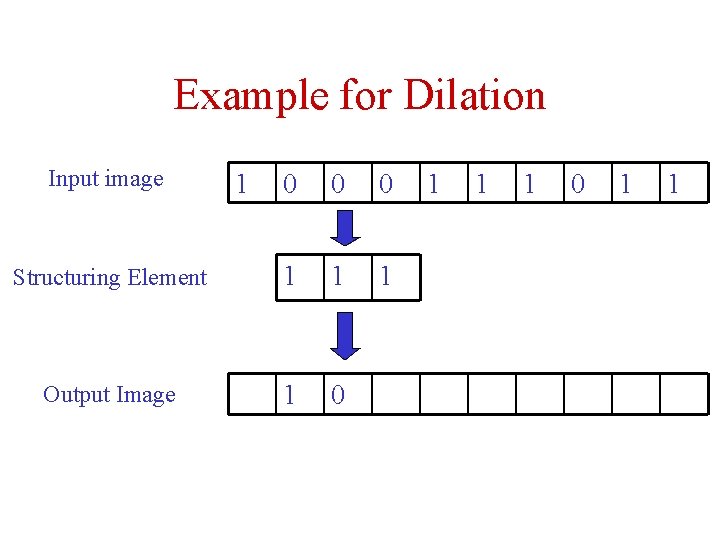
Example for Dilation Input image 1 0 0 0 Structuring Element 1 1 1 Output Image 1 0 1 1

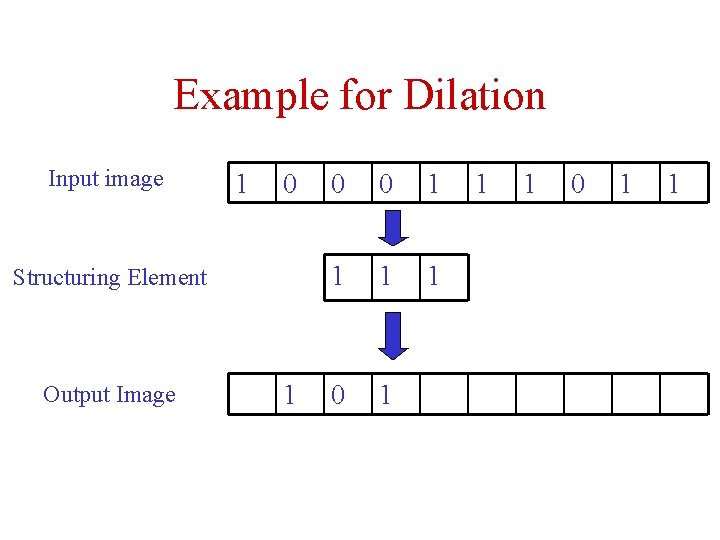
Example for Dilation Input image 1 0 Structuring Element Output Image 1 0 0 1 1 1 0 1 1

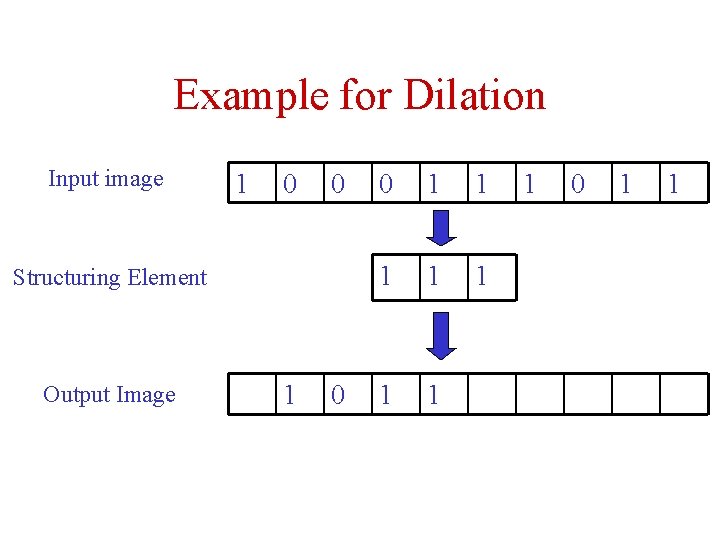
Example for Dilation Input image 1 0 0 Structuring Element Output Image 1 0 0 1 1 1 1 0 1 1

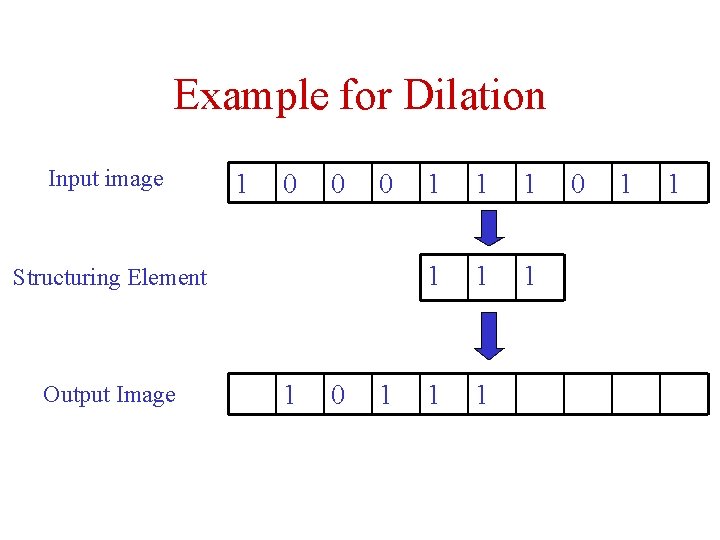
Example for Dilation Input image 1 0 0 0 Structuring Element Output Image 1 0 1 1 1 1 1 0 1 1

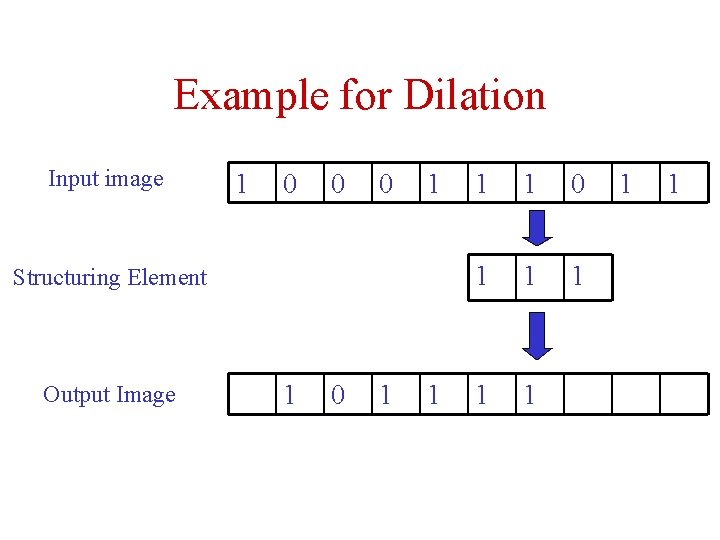
Example for Dilation Input image 1 0 0 0 1 Structuring Element Output Image 1 0 1 1 1 1 1

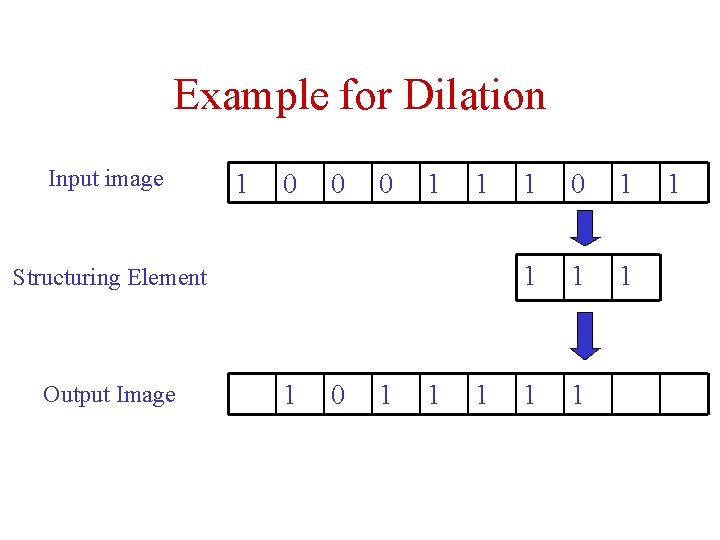
Example for Dilation Input image 1 0 0 0 1 1 Structuring Element Output Image 1 0 1 1 1 1 1

Example for Dilation Input image 1 0 0 0 1 1 1 Structuring Element Output Image 1 0 1 1 1 1 1

2 D Morphological Operations

Binary Morphological Processing • Non-linear image processing technique – Order of sequence of operations is important • Linear: (3+2)*3 = (5)*3=15 3*3+2*3=9+6=15 • Non-linear: (3+2)2 + (5)2 =25 [sum, then square] (3)2 + (2)2 =9+4=13 [square, then sum] • Based on geometric structure • Used for edge detection, noise removal and feature extraction • Used to ‘understand’ the shape/form of a binary image Roger S. Gaborski 23

Image – Set of Pixels • Basic idea is to treat an object within an image as a set of pixels (or coordinates of pixels) • In binary images, pixels that are ‘off’, set to 0, are background appear black. • Foreground pixels (objects) are 1 and appear white

Neighborhood • Set of pixels defined by their location relation to the pixel of interest – Defined by structuring element – Specified by connectivity • Connectivity– ‘ 4 -connected’ – ‘ 8 -connected’

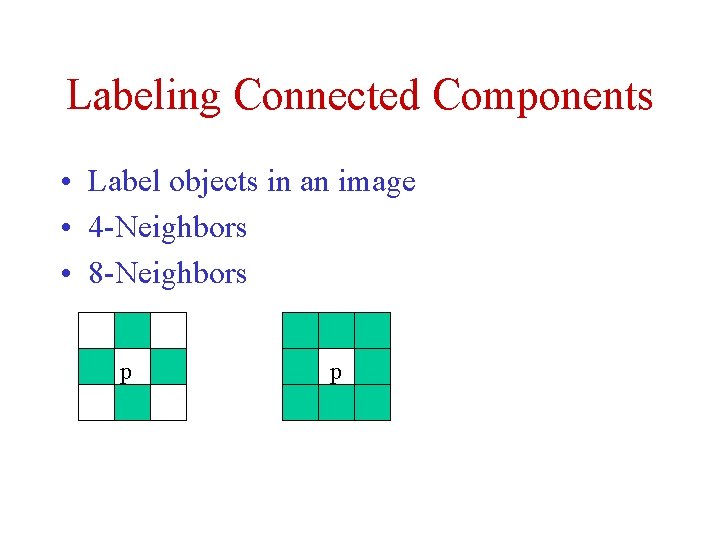
Labeling Connected Components • Label objects in an image • 4 -Neighbors • 8 -Neighbors p p

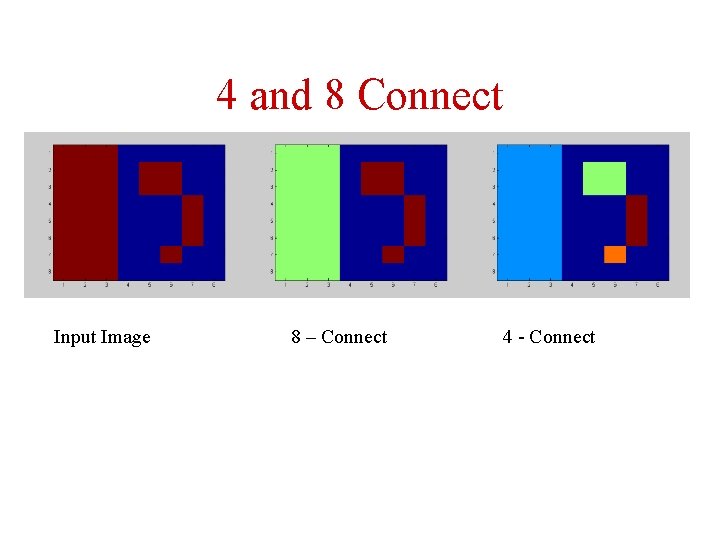
4 and 8 Connect Input Image 8 – Connect 4 - Connect

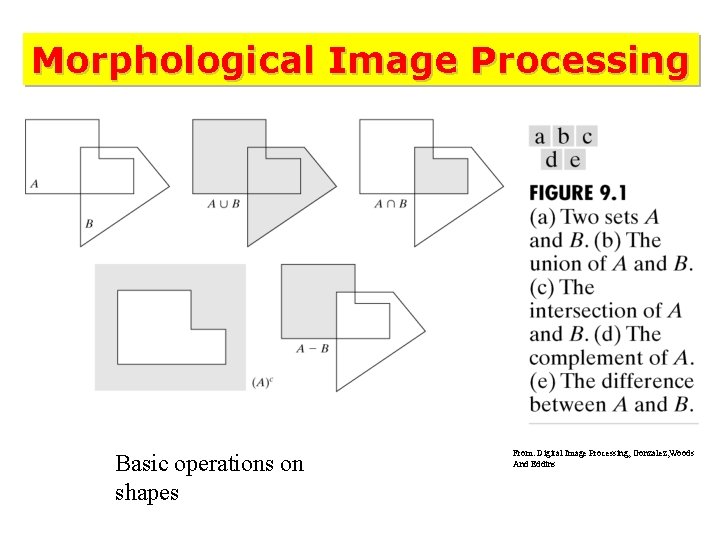
Morphological Image Processing Basic operations on shapes From: Digital Image Processing, Gonzalez, Woods And Eddins

Morphological Image Processing From: Digital Image Processing, Gonzalez, Woods And Eddins

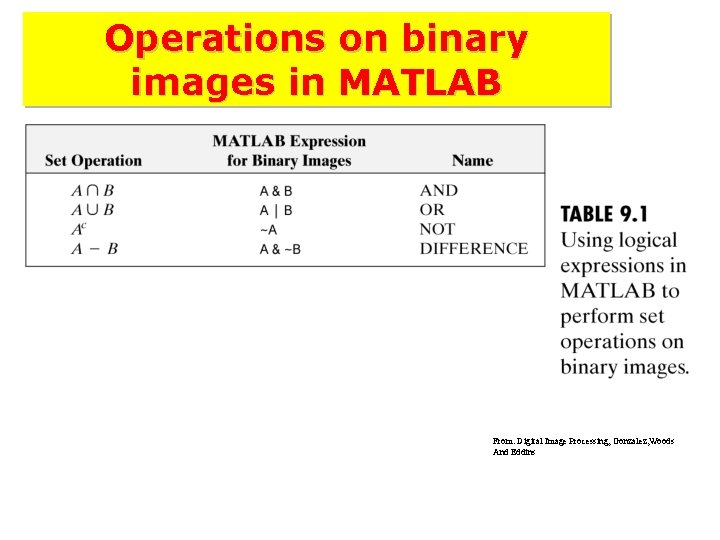
Operations on binary images in MATLAB From: Digital Image Processing, Gonzalez, Woods And Eddins

Translation of Object A by vector b • Define Translation ob object A by vector b: At = { t I 2 : t = a+b, a A } Where I 2 is the two dimensional image space that contains the image • Definition of DILATION is the UNION of all the translations: A B = { t I 2 : t = a+b, a A } for all b’s in B

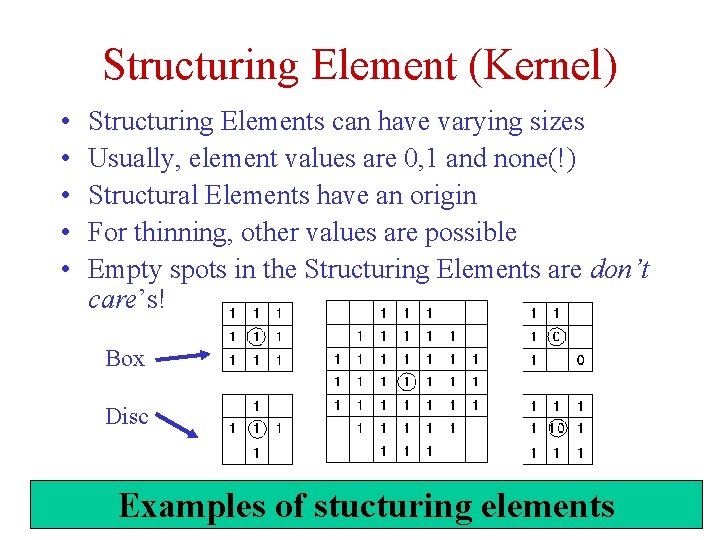
Structuring Element (Kernel) • • • Structuring Elements can have varying sizes Usually, element values are 0, 1 and none(!) Structural Elements have an origin For thinning, other values are possible Empty spots in the Structuring Elements are don’t care’s! Box Disc Examples of stucturing elements 05 -Dec-20 32

Reflection of the structuring element From: Digital Image Processing, Gonzalez, Woods And Eddins

Idea of DILATION versus TRANSLATION A Object B is one point located at (a, 0) A 1: Object A is translated by object B Since dilation is the union of all the translations, A B = At where the set union is for all the b’s in B, the dilation of rectangle A in the positive x direction by a results in rectangle A 1 (same size as A, just translated to the right)

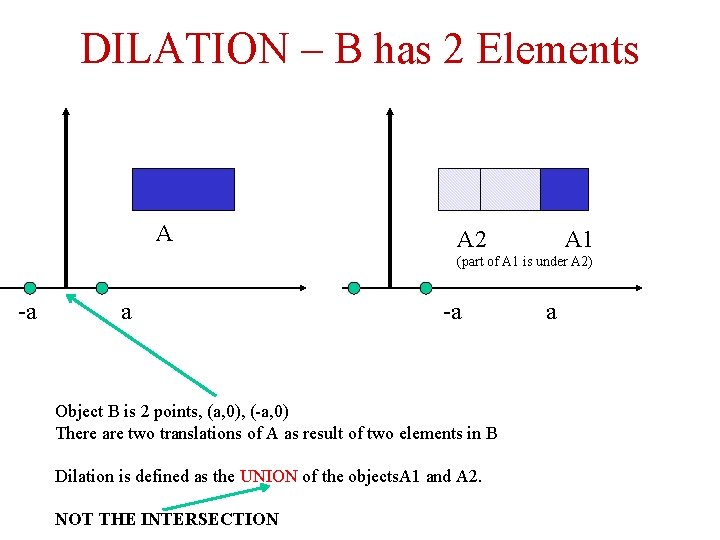
DILATION – B has 2 Elements A A 2 A 1 (part of A 1 is under A 2) -a a -a Object B is 2 points, (a, 0), (-a, 0) There are two translations of A as result of two elements in B Dilation is defined as the UNION of the objects. A 1 and A 2. NOT THE INTERSECTION a

2 D DILATION

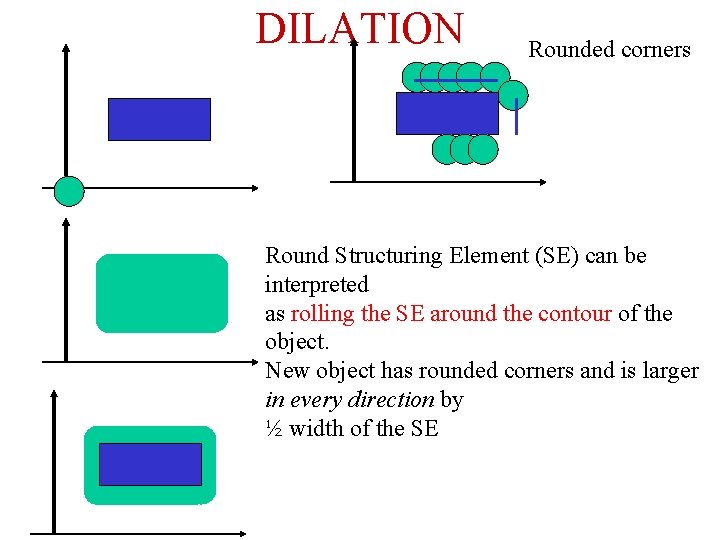
DILATION Rounded corners Round Structuring Element (SE) can be interpreted as rolling the SE around the contour of the object. New object has rounded corners and is larger in every direction by ½ width of the SE

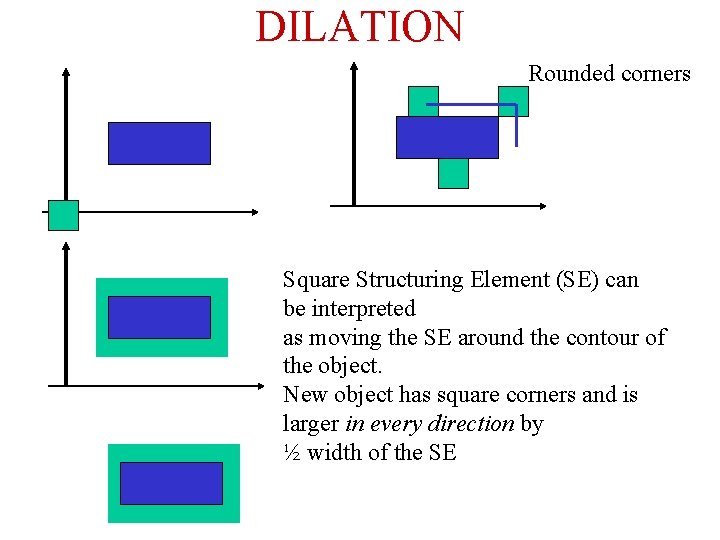
DILATION Rounded corners Square Structuring Element (SE) can be interpreted as moving the SE around the contour of the object. New object has square corners and is larger in every direction by ½ width of the SE

DILATION • The shape of B determines the final shape of the dilated object. • B acts as a geometric filter that changes the geometric structure of A

2 D EROSION

Another important operator • Introduction to Morphological Operators – Used generally on binary images, e. g. , background subtraction results! – Used on gray value images, if viewed as a stack to binary images. • Good for, e. g. , – Noise removal in background – Removal of holes in foreground / background • Check: www. cee. hw. ac. uk/hipr

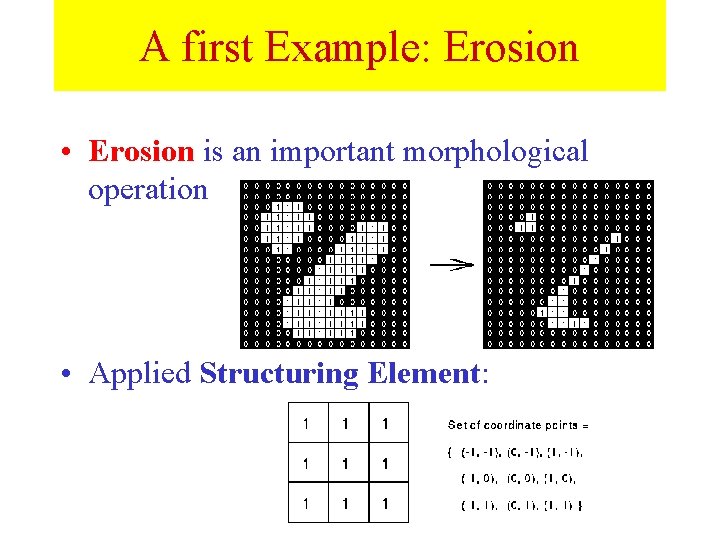
A first Example: Erosion • Erosion is an important morphological operation • Applied Structuring Element:

Dilation versus Erosion • Basic operations • Are dual to each other: – Erosion shrinks foreground, enlarges Background – Dilation enlarges foreground, shrinks background

Erosion • Erosion is the set of all points in the image, where the structuring element “fits into”. • Consider each foreground pixel in the input image – If the structuring element fits in, write a “ 1” at the origin of the structuring element! • Simple application of pattern matching • Input: – Binary Image (Gray value) – Structuring Element, containing only 1 s!

Another example of erosion • White = 0, black = 1, dual property, image as a result of erosion gets darker

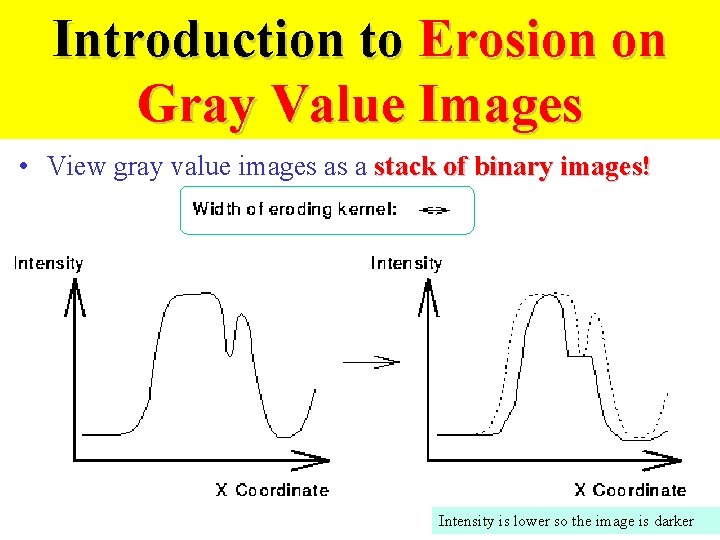
Introduction to Erosion on Gray Value Images • View gray value images as a stack of binary images! Intensity is lower so the image is darker

Erosion on Gray Value Images • Images get darker!

Example: Counting Coins • Counting coins is difficult because they touch each other! • Solution: Binarization and Erosion separates them!

DILATION more details

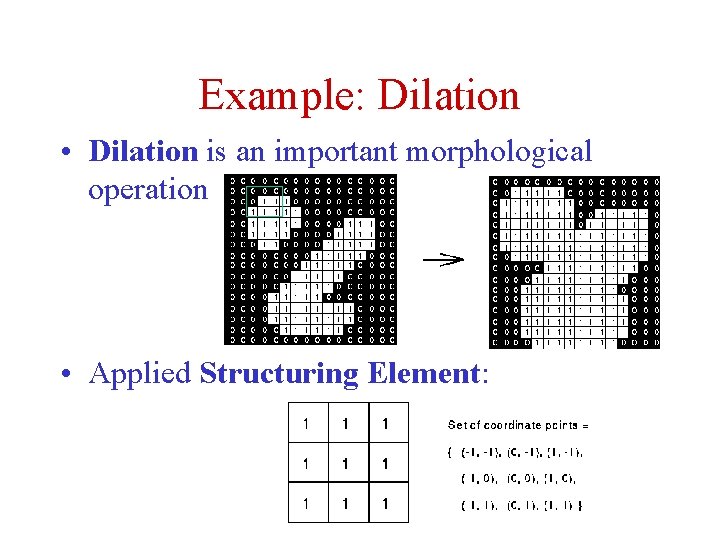
Example: Dilation • Dilation is an important morphological operation • Applied Structuring Element:

Dilation • Dilation is the set of all points in the image, where the structuring element “touches” the foreground. • Consider each pixel in the input image – If the structuring element touches the foreground image, write a “ 1” at the origin of the structuring element! • Input: – Binary Image – Structuring Element, containing only 1 s!!

Another Dilation Example • Image get lighter, more uniform intensity

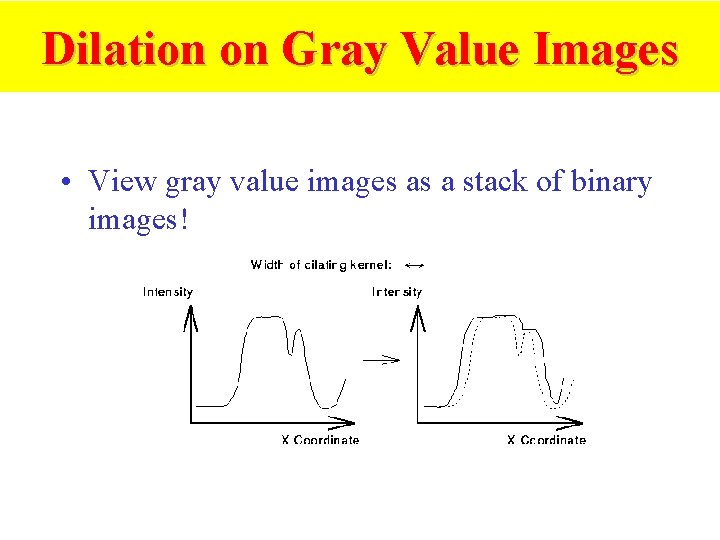
Dilation on Gray Value Images • View gray value images as a stack of binary images!

Dilation on Gray Value Images • More uniform intensity

Edge Detection • 1. 2. 3. Edge Detection Dilate input image Subtract input image from dilated image Edges remain!

From: Digital Image Processing, Gonzalez, Woods And Eddins Illustration of dilation

imdilate IM 2 = IMDILATE(IM, NHOOD) dilates the image IM, where NHOO matrix of 0 s and 1 s that specifies the structuring element neighborhood. This is equivalent to the syntax IIMDILATE(IM STREL(NHOOD)). IMDILATE determines the center element neighborhood by FLOOR((SIZE(NHOOD) + 1)/2). >> se = imrotate(eye(3), 90) se = 0 0 1 0 1 0 0 Roger S. Gaborski 57

Example of Dilation in Matlab >> I = zeros([13 19]); >> I(6, 6: 8)=1; >> I 2 = imdilate(I, se);

Imdilate function in MATLAB IM 2 = IMDILATE(IM, NHOOD) dilates the image IM, where NHOOD is a matrix of 0 s and 1 s that specifies the structuring element neighborhood. This is equivalent to the syntax IIMDILATE(IM, STREL(NHOOD)). IMDILATE determines the center element of the neighborhood by FLOOR((SIZE(NHOOD) + 1)/2). >> se = imrotate(eye(3), 90) se = 0 0 1 0 1 0 0 >> ctr=floor(size(se)+1)/2 ctr = 2 2

MATLAB Dilation Example >> I = zeros([13 19]); >> I(6, 6: 12)=1; >> SE = imrotate(eye(5), 90); >> I 2=imdilate(I, SE); >> figure, imagesc(I) >> figure, imagesc(SE) >> figure, imagesc(I 2)

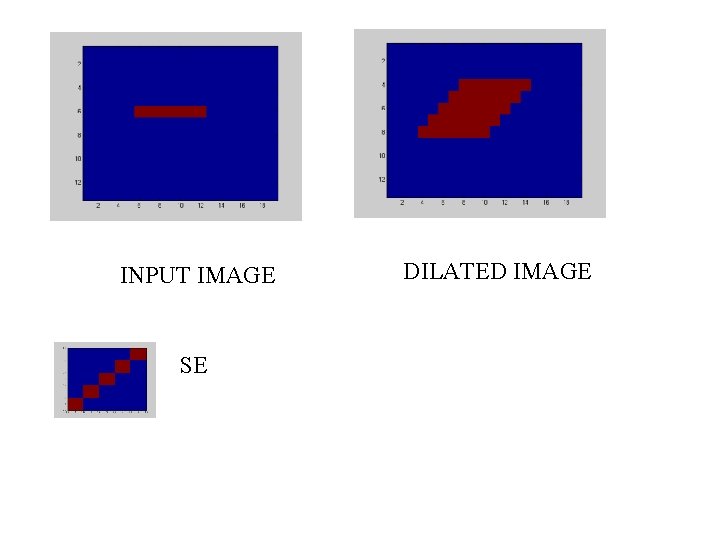
INPUT IMAGE SE DILATED IMAGE

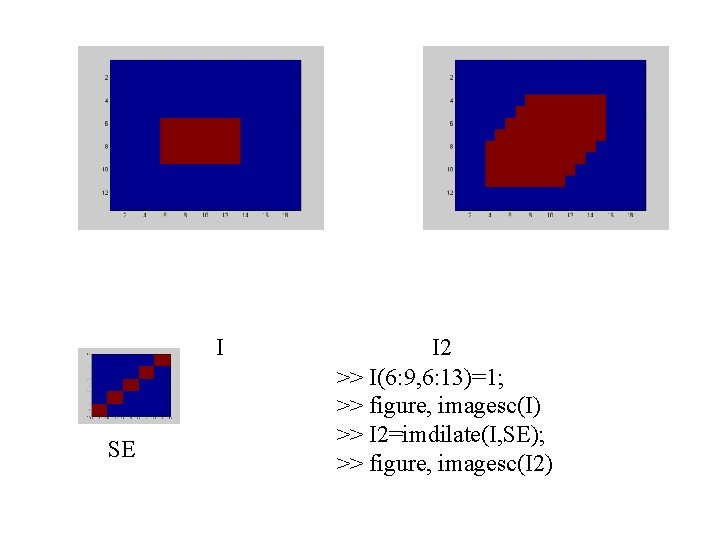
I SE I 2 >> I(6: 9, 6: 13)=1; >> figure, imagesc(I) >> I 2=imdilate(I, SE); >> figure, imagesc(I 2)

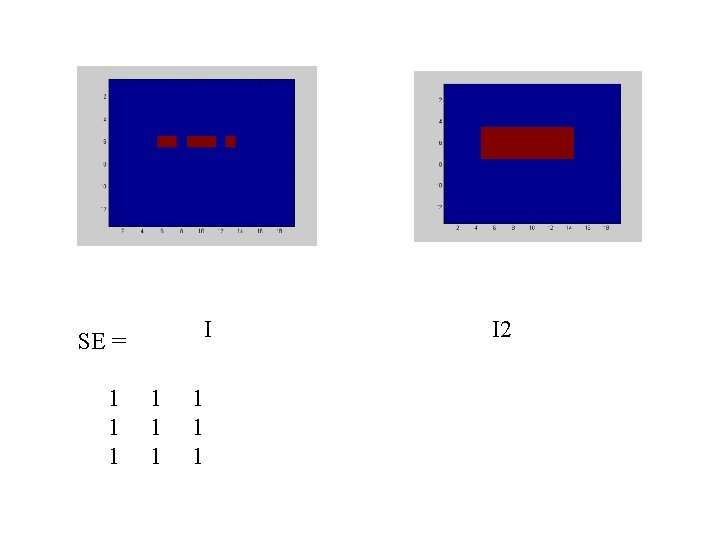
I SE = 1 1 1 1 1 I 2

Dilation and Erosion

Dilation and Erosion • DILATION: Adds pixels to the boundary of an object • EROSIN: Removes pixels from the boundary of an object • Number of pixels added or removed depends on size and shape of structuring element

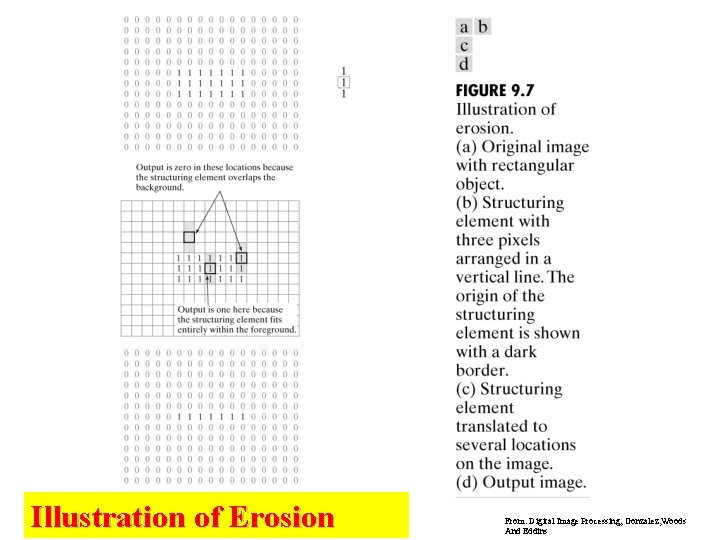
Illustration of Erosion From: Digital Image Processing, Gonzalez, Woods And Eddins

MATLAB Erosion Example 2 pixel wide SE = 3 x 3 I 3=imerode(I 2, SE);

Illustration of erosion From: Digital Image Processing, Gonzalez, Woods And Eddins

Combinations • In most morphological applications dilation and erosion are used in combination • May use same or different structuring elements

Opening & Closing • Important operations • Derived from the fundamental operations – Dilatation – Erosion • Usually applied to binary images, but gray value images are also possible • Opening and closing are dual operations

OPENING

Opening • Similar to Erosion – Spot and noise removal – Less destructive • Erosion next dilation • the same structuring element for both operations. • Input: – Binary Image – Structuring Element, containing only 1 s!

Opening • Take the structuring element (SE) and slide it around inside each foreground region. – All pixels which can be covered by the SE with the SE being entirely within the foreground region will be preserved. – All foreground pixels which can not be reached by the structuring element without lapping over the edge of the foreground object will be eroded away! • Opening is idempotent: Repeated application has no further effects!

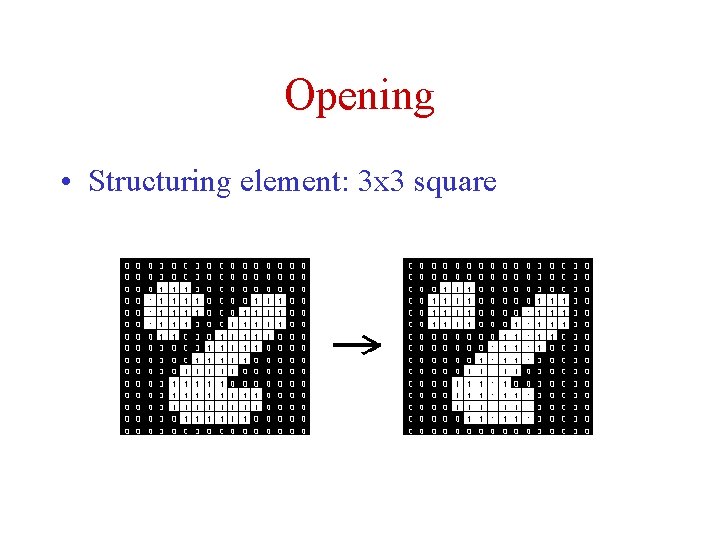
Opening • Structuring element: 3 x 3 square

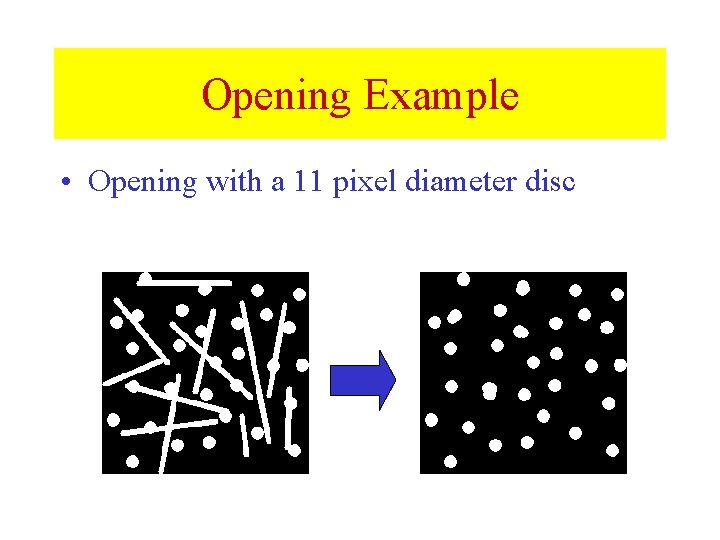
Opening Example • Opening with a 11 pixel diameter disc

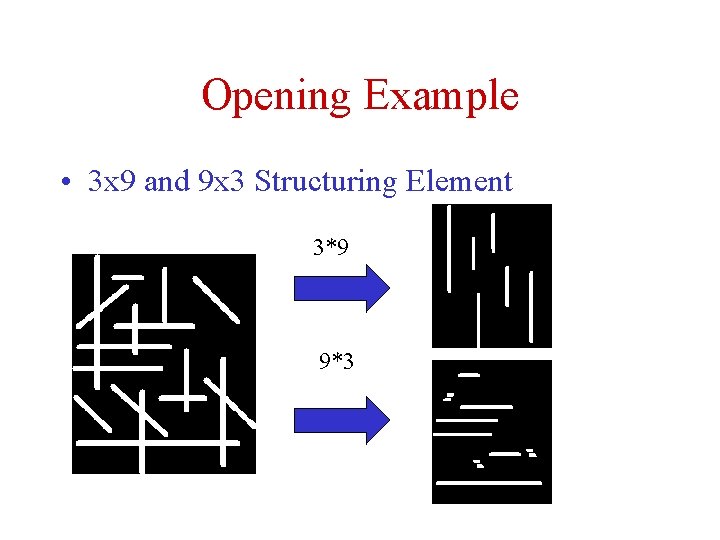
Opening Example • 3 x 9 and 9 x 3 Structuring Element 3*9 9*3

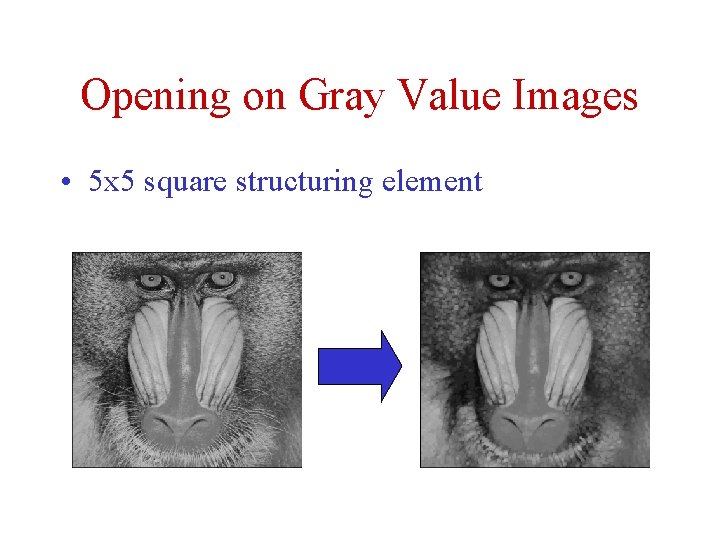
Opening on Gray Value Images • 5 x 5 square structuring element

Use Opening for Separating Blobs • Use large structuring element that fits into the big blobs • Structuring Element: 11 pixel disc

CLOSING

Closing • Similar to Dilation – Removal of holes – Tends to enlarge regions, shrink background • Closing is defined as a Dilatation, followed by an Erosion using the same structuring element for both operations. • Dilation next erosion! • Input: – Binary Image – Structuring Element, containing only 1 s!

Closing • Take the structuring element (SE) and slide it around outside each foreground region. – All background pixels which can be covered by the SE with the SE being entirely within the background region will be preserved. – All background pixels which can not be reached by the structuring element without lapping over the edge of the foreground object will be turned into a foreground. • Opening is idempotent: Repeated application has no further effects!

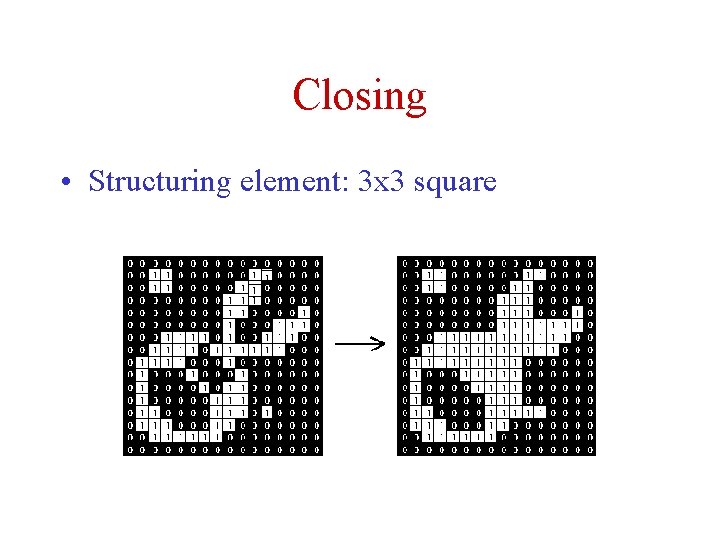
Closing • Structuring element: 3 x 3 square

Closing Example • Closing operation with a 22 pixel disc • Closes small holes in the foreground

Closing Example 1 1. Threshold 2. Closing with disc of size 20 Thresholded closed

Closing Example 2 • Good for further processing: E. g. Skeleton operation looks better for closed image! skeleton of Thresholded and next closed

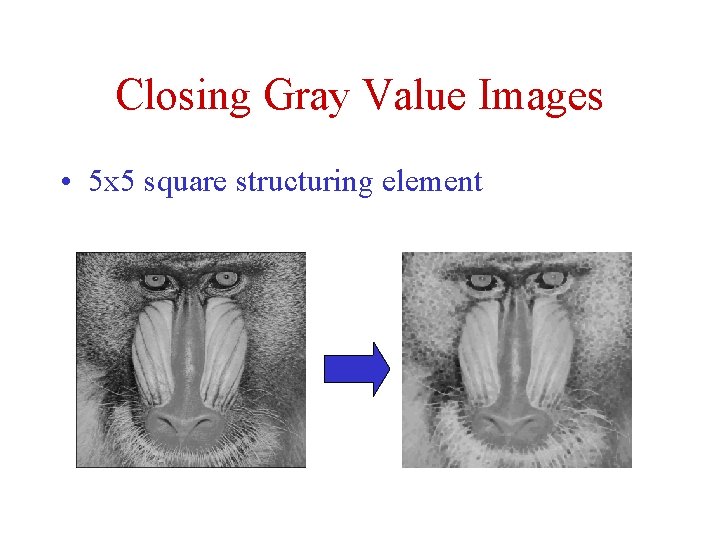
Closing Gray Value Images • 5 x 5 square structuring element

Opening & Closing • Opening is the dual of closing • i. e. opening the foreground pixels with a particular structuring element • is equivalent to closing the background pixels with the same element.

Morphological Opening and Closing • Opening of A by B A B Erosion of A by B, followed by the dilation of the result by B Closing of A by B A B Dilation of A by B, followed by the erosion of the result by B MATLAB: imopen(A, B) imclose(A, B)

MATLAB Function strel • strel constructs structuring elements with various shapes and sizes • Syntax: se = strel(shape, parameters) • Example: – se = strel(‘octagon’, R); – R is the dimension – see help function

• Opening of A by B A B Erosion of A by B, followed by the dilation of the result by B Erosion- if any element of structuring element overlaps with background output is zero FIRST - EROSION >> se = strel('square', 20); fe = imerode(f, se); figure, imagesc(fe), title('fe')

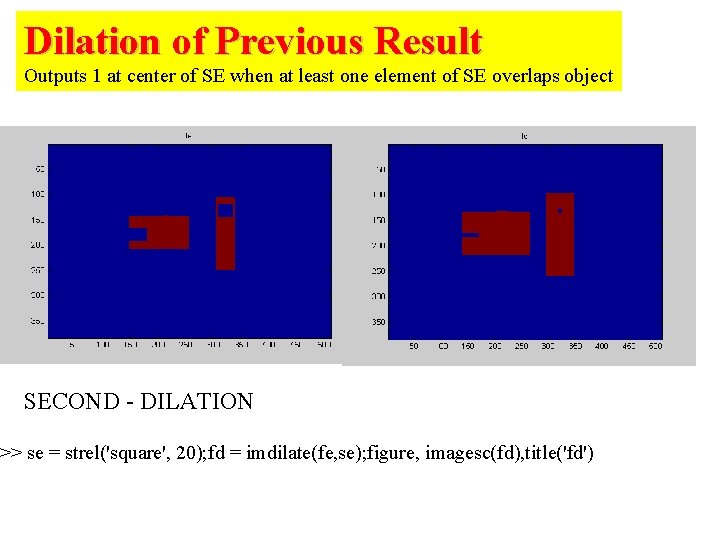
Dilation of Previous Result Outputs 1 at center of SE when at least one element of SE overlaps object SECOND - DILATION >> se = strel('square', 20); fd = imdilate(fe, se); figure, imagesc(fd), title('fd')

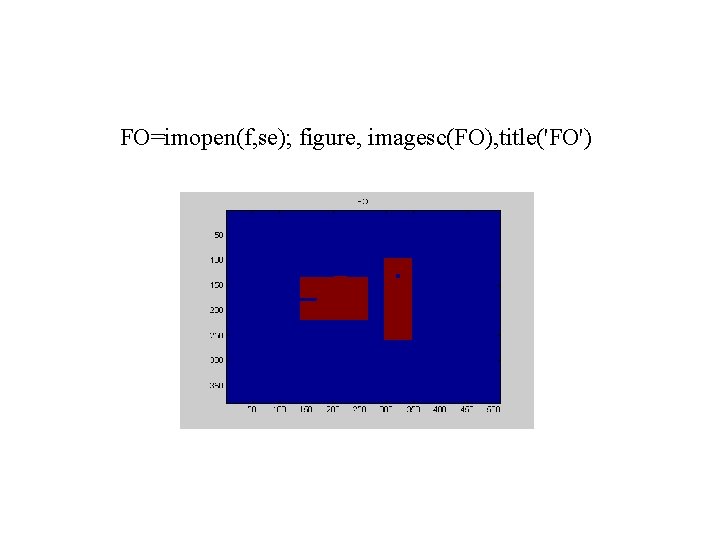
FO=imopen(f, se); figure, imagesc(FO), title('FO')

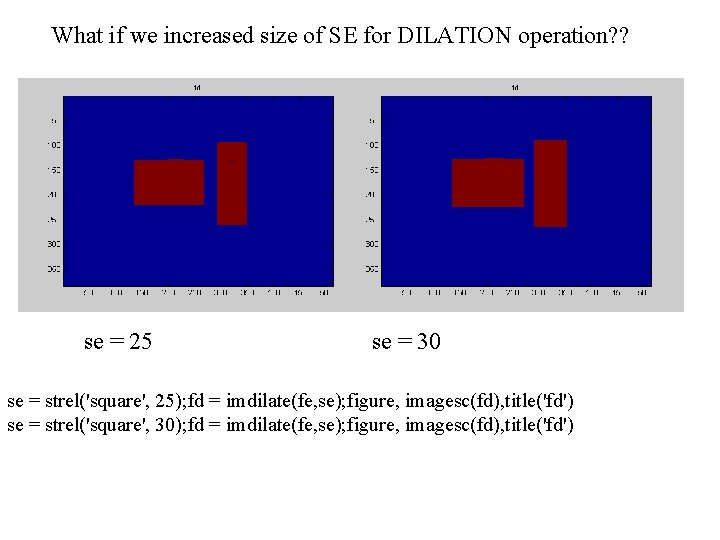
What if we increased size of SE for DILATION operation? ? se = 25 se = 30 se = strel('square', 25); fd = imdilate(fe, se); figure, imagesc(fd), title('fd') se = strel('square', 30); fd = imdilate(fe, se); figure, imagesc(fd), title('fd')

Closing of A by B A B Dilation of A by B Outputs 1 at center of SE when at least one element of SE overlaps object se = strel('square', 20); fd = imdilate(f, se); figure, imagesc(fd), title('fd')

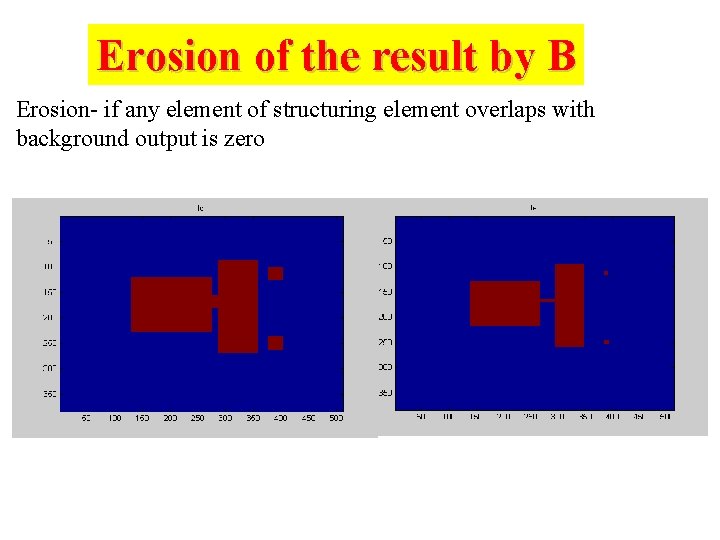
Erosion of the result by B Erosion- if any element of structuring element overlaps with background output is zero

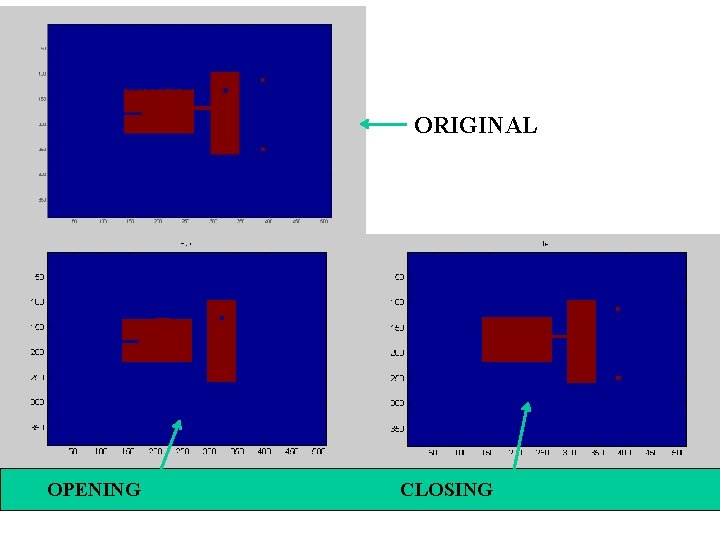
ORIGINAL OPENING CLOSING

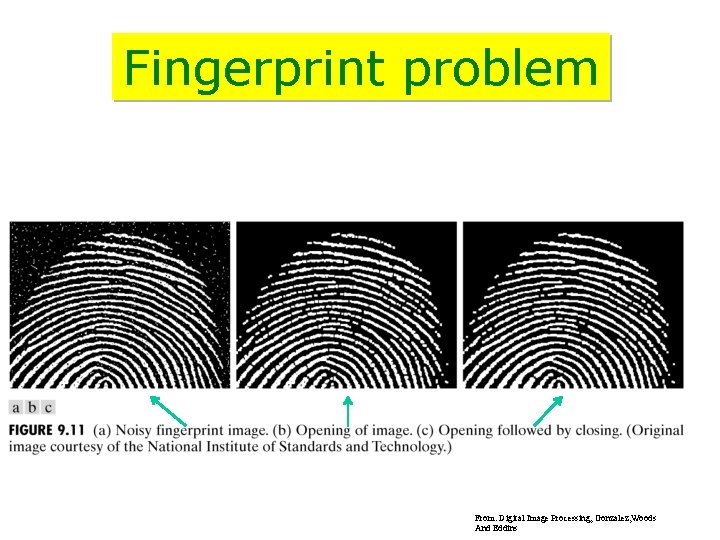
Fingerprint problem From: Digital Image Processing, Gonzalez, Woods And Eddins

Sources Used 1. Volker Krüger 2. Rune Andersen 3. . Roger S. Gaborski