Introduction to Modelling 1 Features of a Model

Introduction to Modelling 1

Features of a Model A model according to Stachowiak exhibits the following features: Mapping feature A model is based on an original (there is a subject). Reduction feature A model only reflects a (relevant) selection of an original's properties. Pragmatic feature A model needs to be usable in place of an original with respect to some purpose. Most models found in software engineering are specification models (prescriptive models) and typically the "original" does not exist when the model is created. This is not always the case, doing data analysis can be understood as making a model given a subject (the data being analyzed). 2

Two basic model roles • Being a model is not an intrinsic property but a role played in relation to what is being modeled. • Two basic model roles are defined by Thomas Kϋhne [1]: token and type. 3

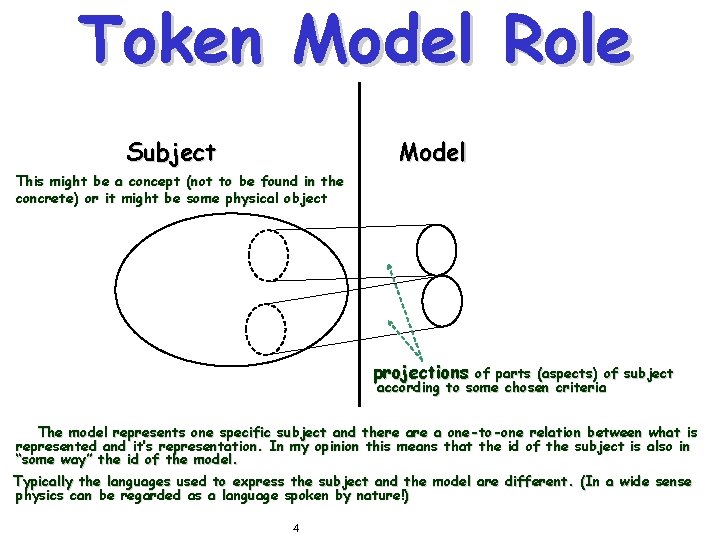
Token Model Role Subject Model This might be a concept (not to be found in the concrete) or it might be some physical object projections of parts (aspects) of subject according to some chosen criteria The model represents one specific subject and there a one-to-one relation between what is represented and it’s representation. In my opinion this means that the id of the subject is also in “some way” the id of the model. Typically the languages used to express the subject and the model are different. (In a wide sense physics can be regarded as a language spoken by nature!) 4

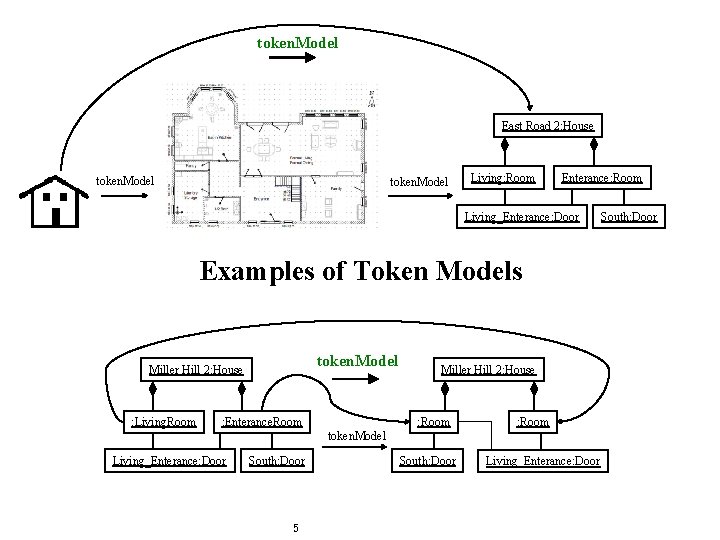
token. Model East Road 2: House token. Model Living: Room Enterance: Room Living_Enterance: Door Examples of Token Models token. Model Miller Hill 2: House : Living. Room : Enterance. Room Miller Hill 2: House : Room token. Model Living_Enterance: Door South: Door 5 South: Door Living_Enterance: Door South: Door

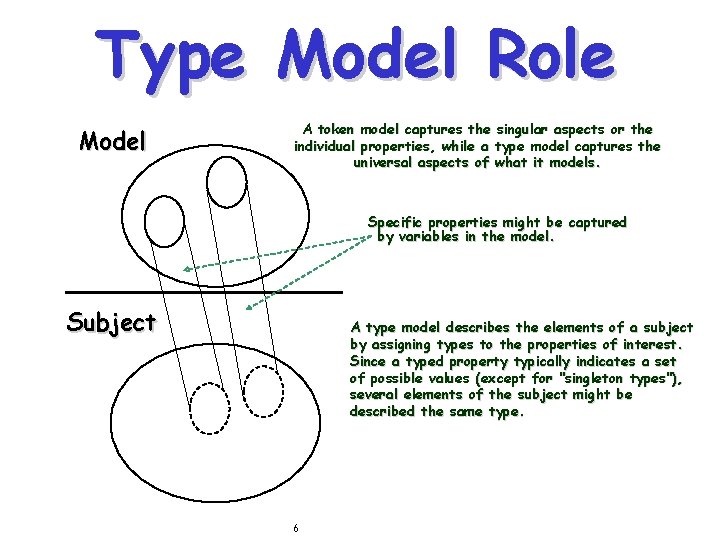
Type Model Role Model A token model captures the singular aspects or the individual properties, while a type model captures the universal aspects of what it models. Specific properties might be captured by variables in the model. Subject A type model describes the elements of a subject by assigning types to the properties of interest. Since a typed property typically indicates a set of possible values (except for "singleton types"), several elements of the subject might be described the same type. 6

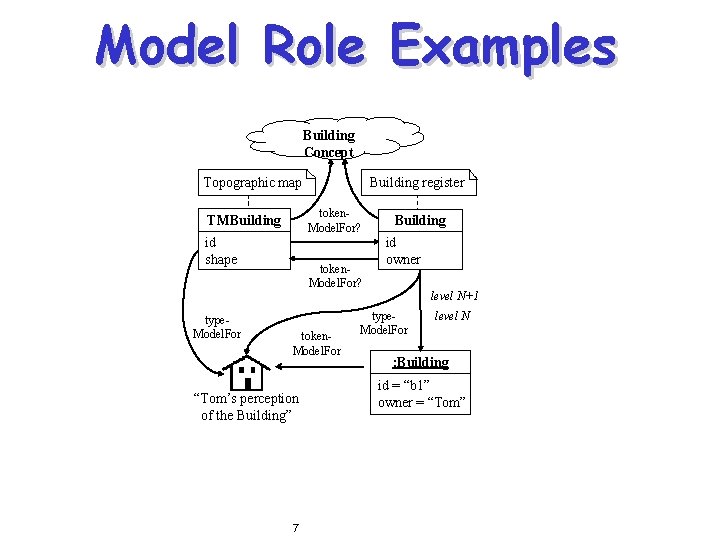
Model Role Examples Building Concept Building register Topographic map token. Model. For? TMBuilding id shape type. Model. For token. Model. For? token. Model. For “Tom’s perception of the Building” 7 Building id owner level N+1 type. Model. For level N : Building id = “b 1” owner = “Tom”

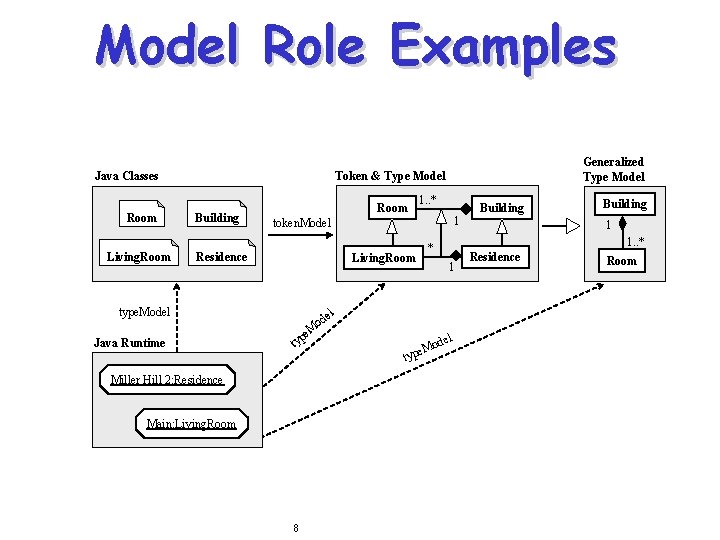
Model Role Examples Java Classes Room Living. Room Generalized Type Model Token & Type Model Building 1 token. Model Residence Living. Room type. Model Java Runtime 1. . * Room 1 od M de Mo e p y t Miller Hill 2: Residence Main: Living. Room 8 1 1. . * * el e typ Building l Residence Room

Why Do We Model? • Models give us a template that guides us in constructing a system. • If you want to make a building you first make a blueprint of the building to make, in the same way you should make a model of the system you want to make. As the complexity of systems increases, so does the importance of good modeling techniques. • Models help us visualize a system at different levels of abstraction, this makes it easier to manage complexity and to understand the system. 9

More Arguments Why Do We Model? • It is not expensive to experiment with multiple solutions when you operate on a high level of abstraction. • Models document the decisions we have made. • Models help for communication between different stakeholders. 10

References [1] Thomas Kϋhne. Matters of (meta-) modeling. Software and Systems Modeling (So. Sy. M), pages: 369 -385, December 2006. 11