Introduction to Matlab Programming Mfiles Scripts and function

Introduction to Matlab Programming

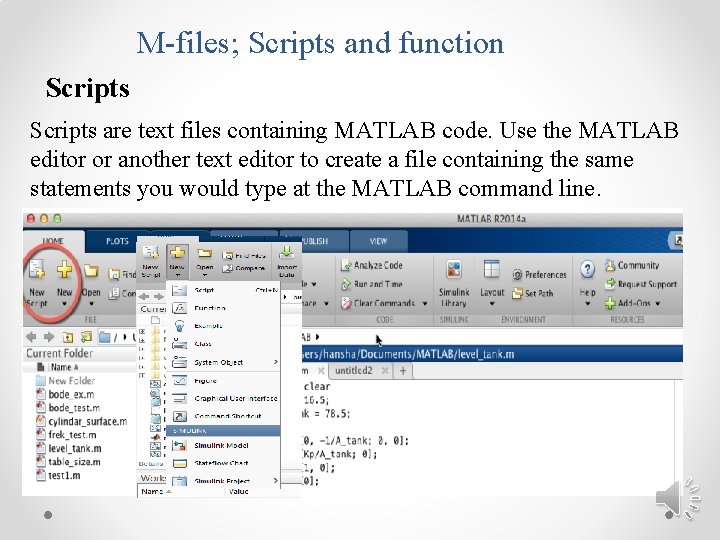
M-files; Scripts and function Scripts are text files containing MATLAB code. Use the MATLAB editor or another text editor to create a file containing the same statements you would type at the MATLAB command line.

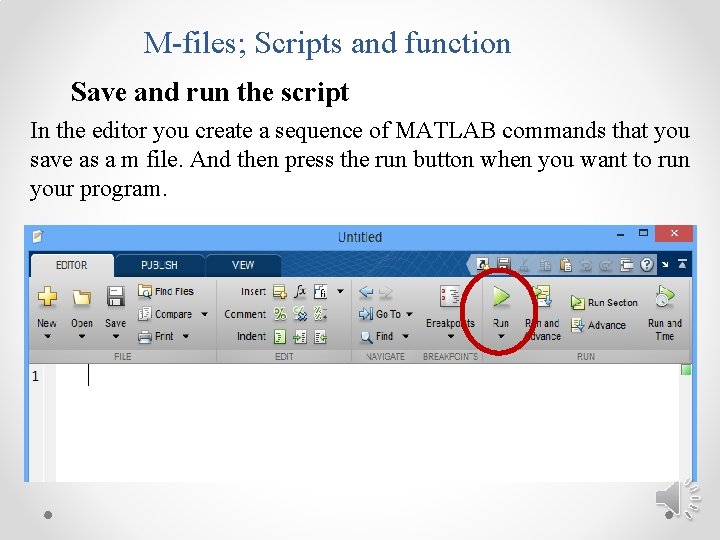
M-files; Scripts and function Save and run the script In the editor you create a sequence of MATLAB commands that you save as a m file. And then press the run button when you want to run your program.

M-files; Scripts and function Scripts A script is a collection of MATLAB commands and functions that is bundled together in a m file. When run the script, all the commands are executed sequentially

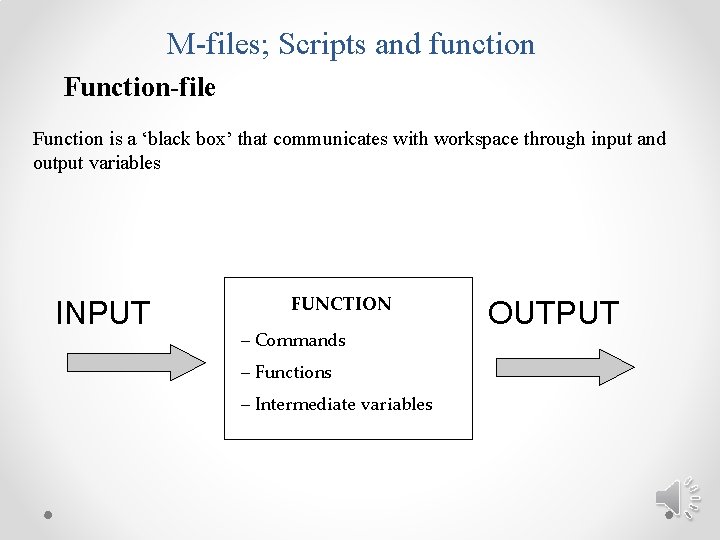
M-files; Scripts and function Function-file Function is a ‘black box’ that communicates with workspace through input and output variables INPUT FUNCTION – Commands – Functions – Intermediate variables OUTPUT

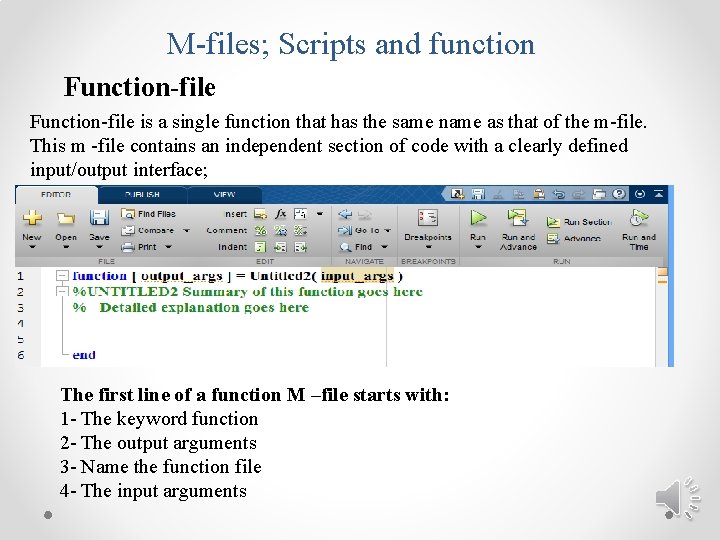
M-files; Scripts and function Function-file is a single function that has the same name as that of the m-file. This m -file contains an independent section of code with a clearly defined input/output interface; The first line of a function M –file starts with: 1 - The keyword function 2 - The output arguments 3 - Name the function file 4 - The input arguments

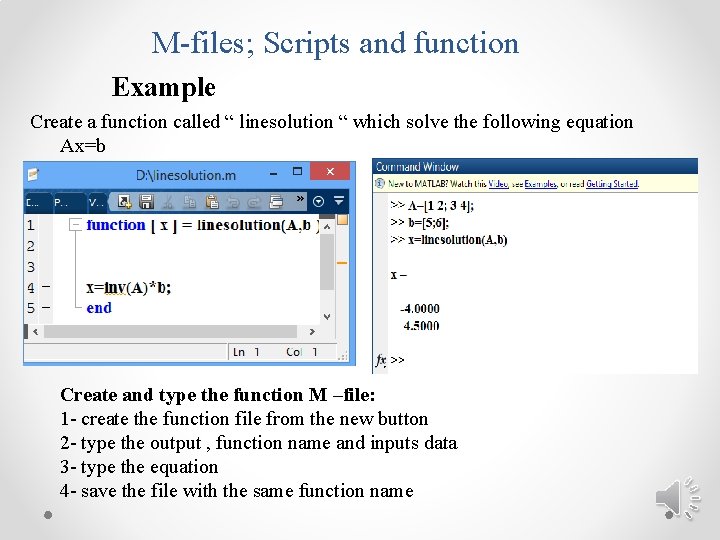
M-files; Scripts and function Example Create a function called “ linesolution “ which solve the following equation Ax=b Create and type the function M –file: 1 - create the function file from the new button 2 - type the output , function name and inputs data 3 - type the equation 4 - save the file with the same function name

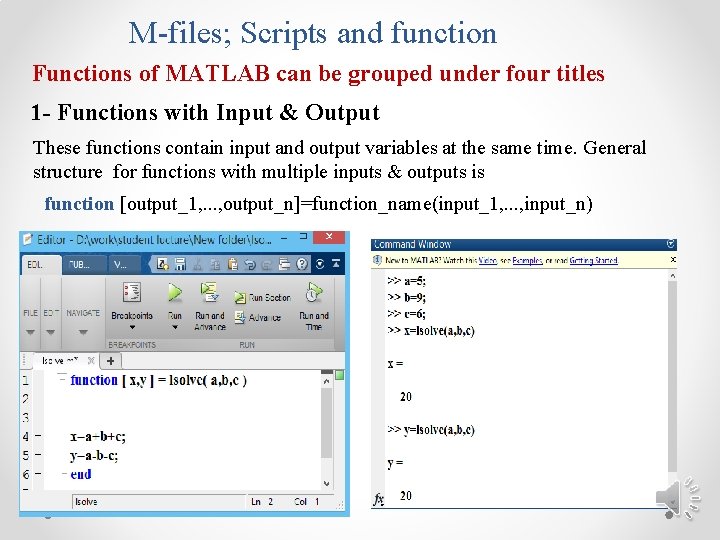
M-files; Scripts and function Functions of MATLAB can be grouped under four titles 1 - Functions with Input & Output These functions contain input and output variables at the same time. General structure for functions with multiple inputs & outputs is function [output_1, . . . , output_n]=function_name(input_1, . . . , input_n)

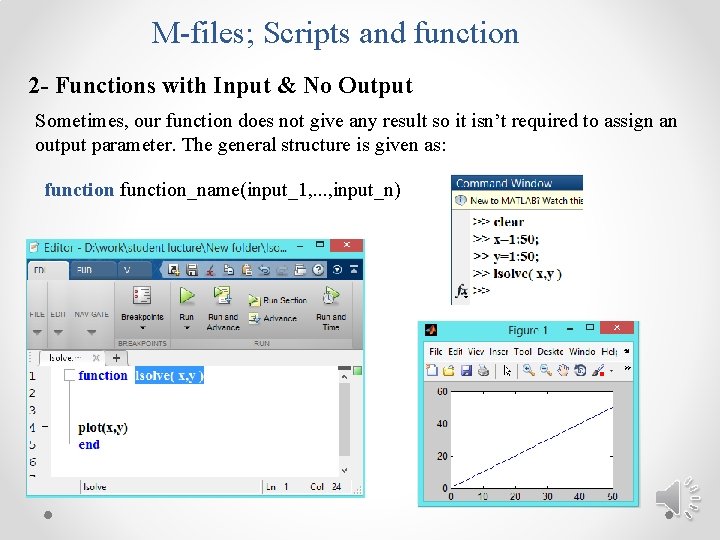
M-files; Scripts and function 2 - Functions with Input & No Output Sometimes, our function does not give any result so it isn’t required to assign an output parameter. The general structure is given as: function_name(input_1, . . . , input_n)

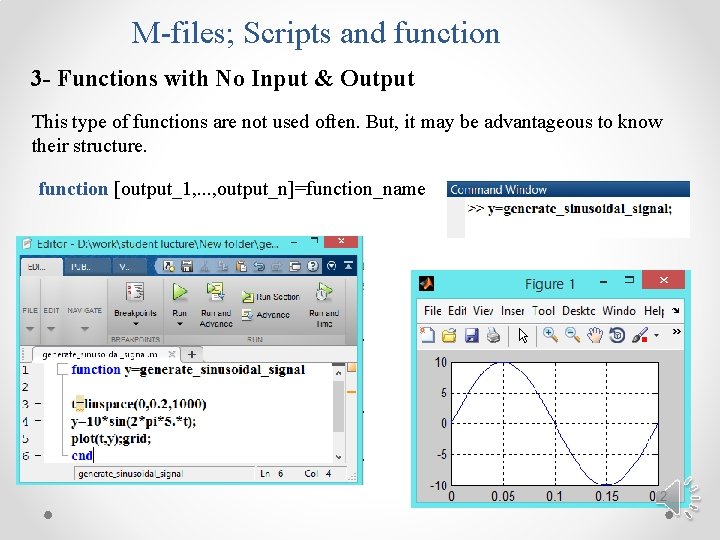
M-files; Scripts and function 3 - Functions with No Input & Output This type of functions are not used often. But, it may be advantageous to know their structure. function [output_1, . . . , output_n]=function_name

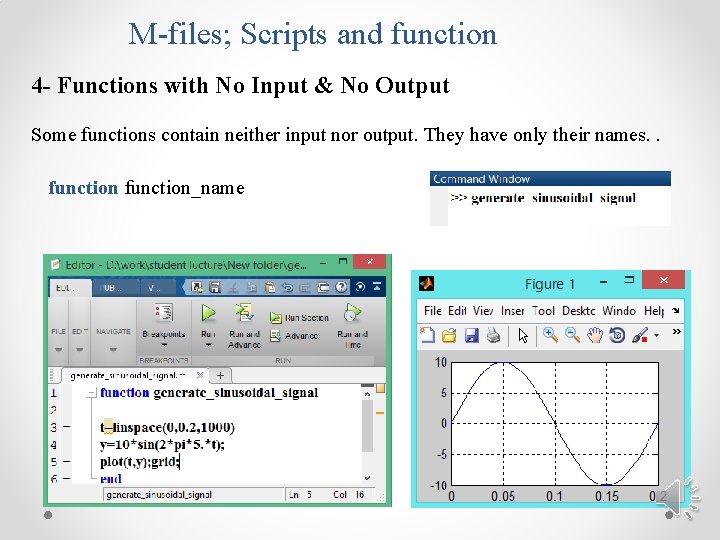
M-files; Scripts and function 4 - Functions with No Input & No Output Some functions contain neither input nor output. They have only their names. . function_name

M-files; Scripts and function The important difference between a script file and function file Script 1 - A collection of commands that you would execute in the command window 3 - Do not accept input arguments or return output arguments 2 - Used for automate repetitive tasks Function 1 - Operate on information ( input) fed into them and return outputs 2 - Have a separate workspace and internal variables that is only valid inside the function 3 - Defined functions work the same way as the built-in functions 4 - Useful for extending the M ATLAB language for your application

M-files; Scripts and function Type of function 1 - The primary function: The primary function is the first function in an M- file and typically contains the main program. primary function is the only function in an M- file that you can call from the MATLAB command line or from another Mfile function. 2 - Anonymous functions: enable to create a simple function without needing to create an M- file for it. Anonymous function can be construct either at the MATLAB command line or from within another function or script. Thus, anonymous functions provide a quick way of making a function from any MATLAB expression without the need to create, name, and save a file. 3 - Sub functions: are placed in the primary function and are called by the primary function. You can use multiple functions within a single primary function M- file.

M-files; Scripts and function Function-file 4 - Nested functions are functions defined within another function. They can help to improve the readability of your program and also give you more exible access to variables in the M- le. The difference between nested functions and sub functions is that sub functions normally cannot be accessed outside of their primary function file. 5 - Overloaded functions are functions that respond differently to different types of input arguments. They are similar to overloaded functions in any objectoriented language. For example, an overloaded function can be created to treat integer inputs differently than inputs of class double. 6 - Private functions enable you to restrict access to a function. They can be called only from an M- le function in the parent directory.

M-files; Scripts and function 2 - Anonymous functions: enable to create a simple function without needing to create an M- file for it. Anonymous function can be construct either at the MATLAB command line or from within another function or script. Thus, anonymous functions provide a quick way of making a function from any MATLAB expression without the need to create, name, and save a file. function handle Variable name fhandle = @ (var) (fun) arglist expression

M-files; Scripts and function Example Single -Input Arguments: Create anonymous function having one input. For example to create a simple function called sq to calculate the square of a number, type sq = @ (x) (x. ^2); To execute the function, type the name of the function handle, followed by any input arguments enclosed in parentheses. >> sq(5) >> sq([5, 7]) ans = 25 49

M-files; Scripts and function Multiple-Input Arguments: Create anonymous functions having more than one input. For example, to define the function (sqrt (x^2 + y^2)) , type >> sqrtsum = @(x, y) sqrt(x. ^2 + y. ^2); To execute the function. >> sqrtsum(3, 4) ans = 5 Example, consider the function z = Ax + By , defining a plane. The scalar variables A and B must be assigned values before create the function handle. >> A = 6; B = 4: >> plane = @(x, y) A*x + B*y; >> z = plane(2, 8) z = 44

M-files; Scripts and function No-Input Arguments: To construct a handle for an anonymous function that has no input arguments, use empty parentheses for the input argument list, as shown by the following: d = @() date; >>d( ) 11 -Mar-2019 Calling One Function within Another: One anonymous function call another to implement function composition. : Example, Consider the function 5*sin(x^3). It is composed of the functions g(y) = 5* sin(y) and f (x) =x^3. >>f = @(x) x. ^3; >>g = @(x) 5*sin(x); >>h = @(x) g(f(x)); >>h(2) ans = 4. 9468

M-files; Scripts and function 3 - Subfunctions are placed in the primary function and are called by the primary function. You can use multiple functions within a single primary function M- file. The next example shows how the MATLAB M-function mean can be superceded by our own definition of the mean, one which gives the root-mean-square value. function y = subfun_demo(a) y = a - mean(a); function w = mean(x) w = sqrt(sum(x. ^2))/length(x); end y = subfn_demo([4, -4]) y = 1. 1716 -6. 8284 >>a=[4, -4]; >>b = a - mean(a) B = 4 -4

Input and output Input statements Fixed values Used to create constant data , vector or matrix A=5 B=7 A=(1 2 3 4) A=[1 2 3; 3 4 5; 9 5 4] Used function “ input” The input function is used in an assignment statement. To call it, a string is passed, which is the prompt that will appear on the screen, and whatever the user types will be stored in the variable named on the left of the assignment statement. If number input is desired: speed= input('Enter the speed: ') Enter the speed : 1000 speed = 1000

Input and output num = input('Enter a number: ') Enter a number: k Error using input Undefined function or variable ‘k'. Enter a number: 100 number = 100 If letter input is desired: letter= input('Enter the letter: ', 's') Enter the letter: k Enter the letter: 100 letter= k letter= 100

Input and output Output statements Display function “disp” The simplest output function in MATLAB is (disp) , which is used to display the result of an expression or a string without assigning any value to the default variable ans. disp ('variable') disp(4^3) variable 64 disp(['The value of x =', num 2 str(x)]); The value of x =

Input and output Output statements Print function “fprintf” fprintf (' The value of x = %fn', x); The value of x = To print two or more values fprintf('The value of x = %3 d and y = %3 dn', x, y) The value of x = 5 and y = 9 Component of a format specifier % + 3 d n % A single % character always marks the beginning of a format + Format Flags d Format Conversion Specifiers n Escape Characters in Format Strings

Input and output Output statements Format Conversion Specifiers Displaying Decimal Data Decimal (integer) data is displayed with the x=5. 125487 %d format conversion specified. fprintf('The value of x = %dn', x) The value of x = 5. 125487 e+00 Numbers of Decimal Data fprintf('The value of x = %. 2 dn', x) The value of x = 5. 13 e+00 fprintf('The value of x = %. 5 dn', z) The value of x = 5. 12549 e+00

Input and output Output statements Format Conversion Specifiers Displaying Floating-Point Data Floating-point data can be displayed with the %f, or specifiers. x=5. 125487 fprintf('The value of x %g format conversion = %fn', x) The value of x = 5. 125487 Displaying Character Data Character data may be displayed with the %c or %s format conversion specifiers. fprintf('The value of x = %cn', ‘H') The value of x = H fprintf('The value of x = %sn', 'string') The value of x = string

Input and output Output statements Format Conversion Specifiers Add spacing before the numbers fprintf('The value of x = %fn', x) The value of x = 5. 125487 fprintf('The value of x = %20 fn', x) The value of x = fprintf('The value of x = 20%fn', x) 5. 125487 The value of x = 205. 125487 Escape Characters in Format Strings n New line. >> fprintf('The value of x = %fn', x) The value of x = 5. 125487 >> t Horizontal tab. >> fprintf('The value of x = %ft', x) The value of x = 5. 125487 >>

Input and output How Format Strings Are Used 1 - The fprintf function contains a format string followed by zero or more values to print out. 2 - When the fprintf function is executed, the list of output values associated with the fprintf function is processed together with the format string. 3 - The function begins at the left end of the variable list and the left end of the format string, and scans from left to right, associating the first value in the output list with the first format descriptor in the format string, and so forth. 4 - The variables in the output list must be of the same type and in the same order as the format descriptors in the format, or unexpected results may be produced.

Input and output Format strings are scanned according to the following rules: 1 - Format strings are scanned in order from left to right. a = 10; b = pi; fprintf('Output: %d c = 'Hello'; %f %sn', a, b, c); Output: 10 3. 141593 Hello 2 - If the scan reaches the end of the format string before the fprintf function runs out of values, the program starts over at the beginning of the format string. a = 10; b= 20; c= 30; d=40; fprintf('Output = %4 dn', a, b, c, d); Output = 10 20 30 40

Input and output fprintf('Output = %4 dn', a, b, c, d); Output = 10 20 Output = 30 40 3 - If the fprintf function runs out of variables before the end of the format string, the use of the format string stops at the first format conversion specifier without a corresponding variable, or at the end of the format string, whichever comes first. a=10; b=15; c=20; fprintf('Output = %4 dn Output = %4. 1 fn', a, b, c); Output = 10 Output = 15. 0 Output = 20 Output = >>

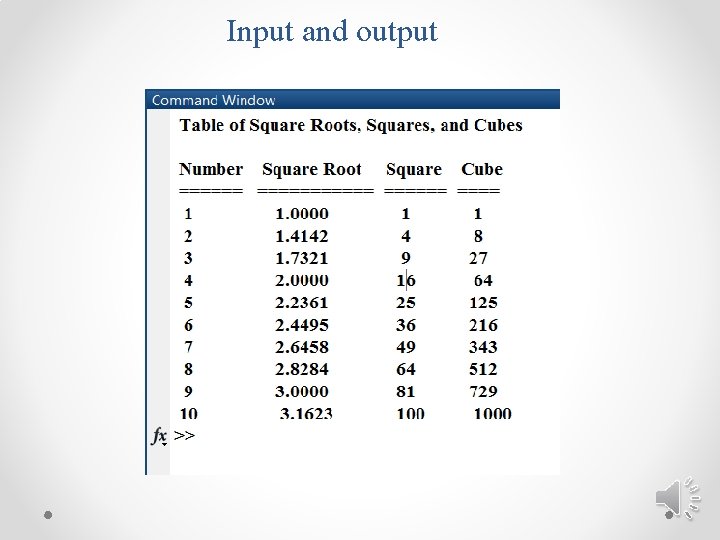
Input and output Example Generates the square roots, squares, and cubes of all integers between 1 and 10 and presents the data in a table with appropriate headings. % Print the title of the table. fprintf(' Table of Square Roots, Squares, and Cubesnn'); % Print column headings fprintf(' Number Square Root Square Cuben'); fprintf(' ===========n'); % Generate the required data ii = 1: 10; square_root = sqrt(ii); square = ii. ^2; cube = ii. ^3; % Create the output array out = [ii' square_root' square' cube']; % Print the data for ii = 1: 10 fprintf (' %2 d %11. 4 f %6 d %8 dn', out(ii, : )); end

Input and output

Input and output Insert data from file The textread Function The textread function reads ASCII files that are formatted into columns of data where each column can be of a different type, and stores the contents of each column in a separate output array. [output data ] = textread(filename, format, n) Output data - is the number of output data Filename - is the name of the file to open Format - is a string containing a description of the type of data in each column n- is the number of lines to read

Input and output Insert data from file Example 1 suppose that file mydata. dat contains the following data: [output data ] = textread(filename, format, n) [x , y , z ] = textread('mydata. dat', '%f, %f ', 1) x= 318 y= 0. 7881 z= 14. 3924

Input and output Insert data from file [x , y , z ] = textread('maydata. dat', '%f, %f ')

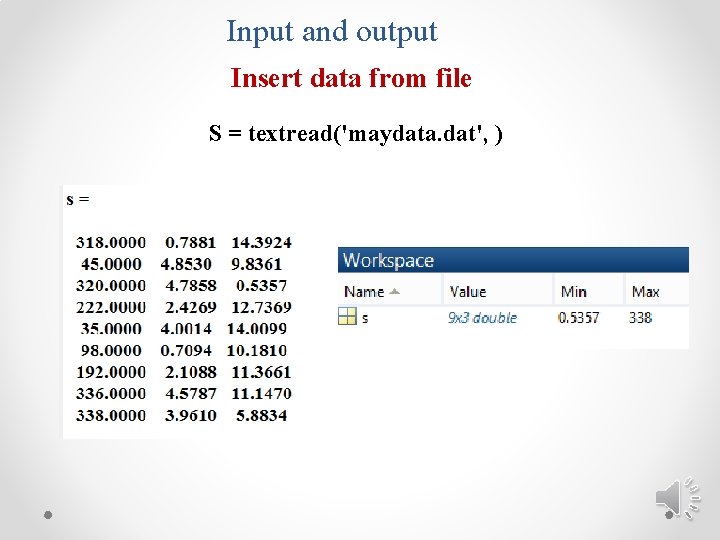
Input and output Insert data from file S = textread('maydata. dat', )

Input and output Insert data from file Example 2 suppose that file maydata. dat contains the following data: Ahmed Ali 80 85 72 90 khaled jalal 80 85 72 90 [output data ] = textread(filename, format, n) [first , last , A , B, C, D ] = textread('maydata. dat', '%s %s %d %d ', 1) first = 'Ahmed' last = ' Ali ' A= 80 B= 85 C= 72 D= 90

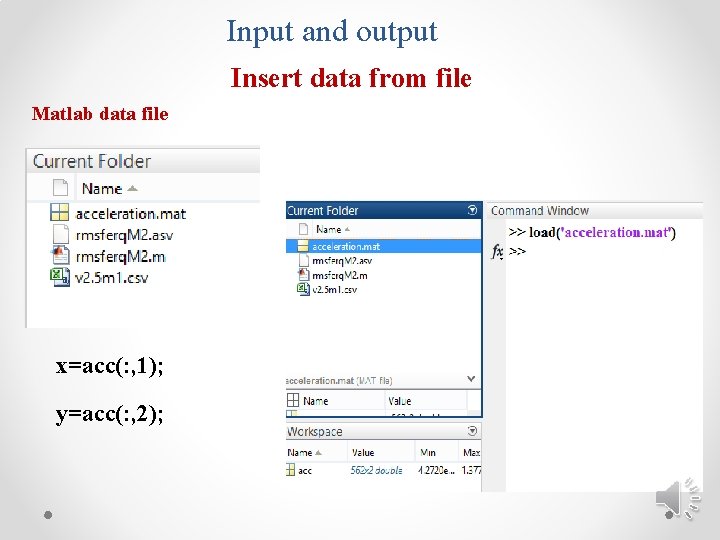
Input and output Insert data from file Matlab data file x=acc(: , 1); y=acc(: , 2);

Input and output Insert data from file Matlab data file x=acc(2: 15, 1); y=acc(2: 15, 2);

Input and output Excel sheet file

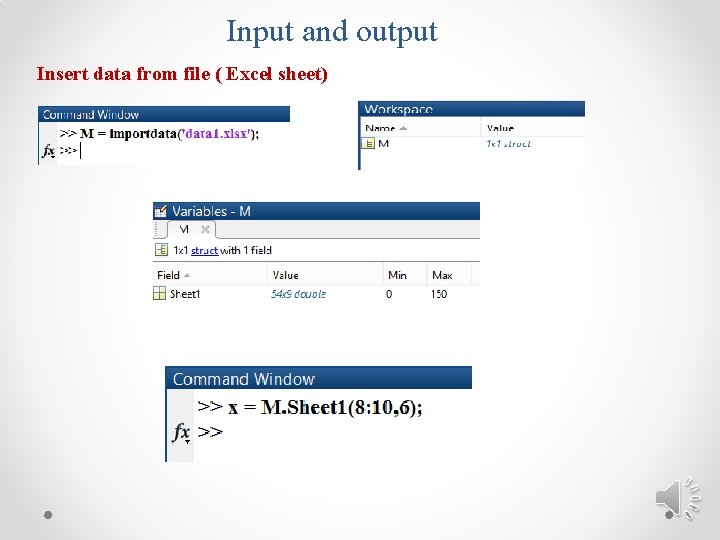
Input and output Insert data from file ( Excel sheet)

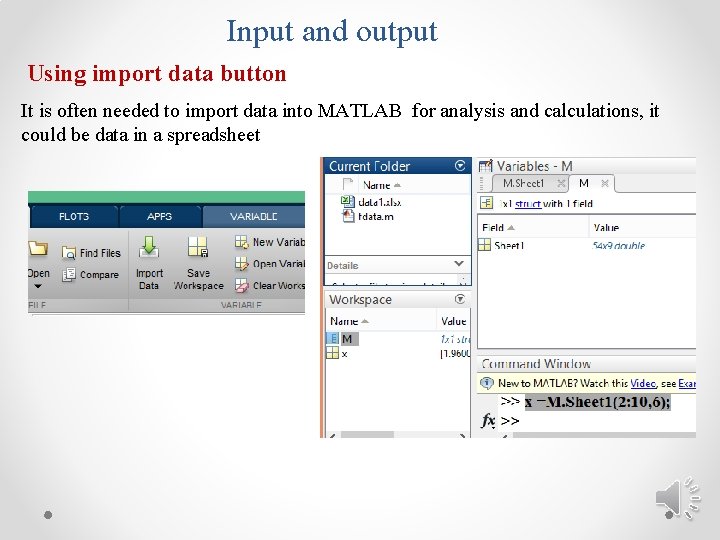
Input and output Using import data button It is often needed to import data into MATLAB for analysis and calculations, it could be data in a spreadsheet