Introduction to Matlab Matlab Basics Matrix Operations S

Introduction to Matlab: Matlab Basics Matrix Operations S. Awad, Ph. D. M. Corless, M. S. E. E. E. C. E. Department University of Michigan-Dearborn

» MATLAB Basics: Matrix Operations Introduction to MATLAB and its Toolboxes U of M-Dearborn ECE Department Matrix Operations Transpose n Addition n Subtraction n Multiplication n Matrix Powers n 2

» MATLAB Basics: Matrix Operations Introduction to MATLAB and its Toolboxes U of M-Dearborn ECE Department Transpose of a Matrix » a = [ 1 2 3; 4 5 6; 7 8 9]; » b = a’; 3

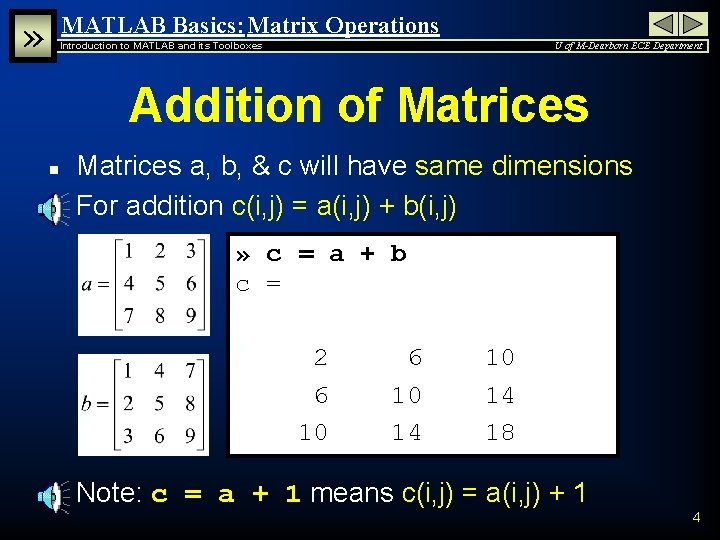
» MATLAB Basics: Matrix Operations Introduction to MATLAB and its Toolboxes U of M-Dearborn ECE Department Addition of Matrices n n Matrices a, b, & c will have same dimensions For addition c(i, j) = a(i, j) + b(i, j) » c = a + b c = 2 6 10 n 6 10 14 18 Note: c = a + 1 means c(i, j) = a(i, j) + 1 4

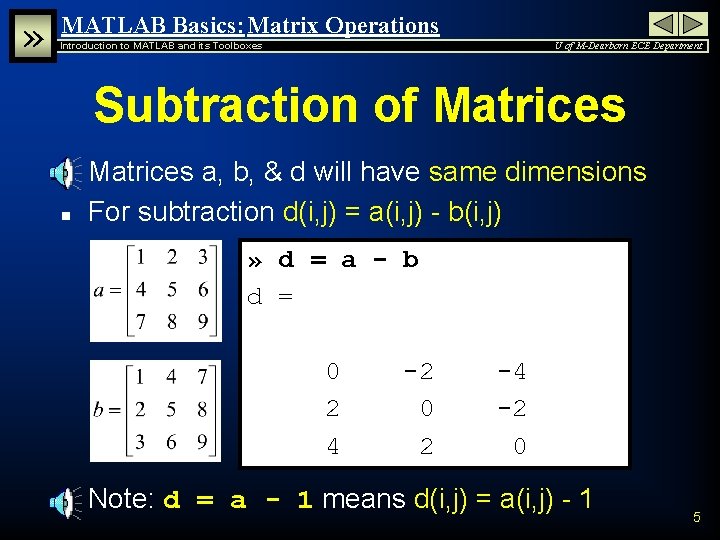
» MATLAB Basics: Matrix Operations Introduction to MATLAB and its Toolboxes U of M-Dearborn ECE Department Subtraction of Matrices n n Matrices a, b, & d will have same dimensions For subtraction d(i, j) = a(i, j) - b(i, j) » d = a - b d = 0 2 4 n -2 0 2 -4 -2 0 Note: d = a - 1 means d(i, j) = a(i, j) - 1 5

» MATLAB Basics: Matrix Operations Introduction to MATLAB and its Toolboxes U of M-Dearborn ECE Department Multiplication of Matrices n n Suppose: a is n x m (n by m) & b is m x l for c = a * b, c must be n x l » a = [ 1 1 1]; » c = a * a’; c = 3 % c = 1 + 1 6

» MATLAB Basics: Matrix Operations Introduction to MATLAB and its Toolboxes U of M-Dearborn ECE Department Matrix Powers n Assume that a is a square matrix, then = a^2 means b = a* a u c = a^5 means a*a*a ub n In general ud n In case p is not an integer (i. e. p = 1/2) ue n = a^p = a*a*a*. . . *a (for p times) = a^0. 5 means a = e*e Note: a^-1 º inv(a) 7