Introduction to Mass Transfer Introduction n i iii

Introduction to Mass Transfer

Introduction n i) iii) Three fundamental transfer processes: Momentum transfer Heat transfer Mass transfer

n n n Mass transfer may occur in a gas mixture, a liquid solution or solid. Mass transfer occurs whenever there is a gradient in the concentration of a species. The basic mechanisms are the same whether the phase is a gas, liquid, or solid.

Definition of Concentration i) Number of molecules of each species present per unit volume (molecules/m 3) ii) Molar concentration of species i = Number of moles of i per unit volume (kmol/m 3) iii) Mass concentration = Mass of i per unit volume (kg/m 3)

Diffusion phenomena n n n Fick’s law: linear relation between the rate of diffusion of chemical species and the concentration gradient of that species. Thermal diffusion: Diffusion due to a temperature gradient. Usually negligible unless the temperature gradient is very large. Pressure diffusion: Diffusion due to a pressure gradient. Usually negligible unless the pressure gradient is very large.

n n Forced diffusion: Diffusion due to external force field acting on a molecule. Forced diffusion occurs when an electrical field is imposed on an electrolyte ( for example, in charging an automobile battery) Knudsen diffusion: Diffusion phenomena occur in porous solids.

n Whenever there is concentration difference in a medium, nature tends to equalize things by forcing a flow from the high to the low concentration region. Before n After The molecular transport process of mass is characterized by the general equation: Rate of transfer process = driving force resistance

Example of Mass Transfer Processes n n Consider a tank that is divided into two equal parts by a partition. Initially, the left half of the tank contains nitrogen N 2 gas while the right half contains O 2 at the same temperature and pressure. When the partition is removed the N 2 molecules will start diffusing into the air while the O 2 molecules diffuse into the N 2. If we wait long enough, we will have a homogeneous mixture of N 2 and O 2 in the tank.

n n Liquid in open pail of water evaporates into air because of the difference in concentration of water vapor at the water surface and the surrounding air. A drop of blue liquid dye is added to a cup of water. The dye molecules will diffuse slowly by molecular diffusion to all parts of the water.

Molecular Diffusion Equation n Fick’s Law z is the molar flux of component A in the direction in kg mol A/s. m 2. is the molecular diffusivity of the molecule A in B in m 2/s is the concentration of A in kg mol/m 3. z is the distance of diffusion in m

Fick’s Law of Diffusion n Molecular diffusion or molecular transport can be defined as the transfer or movement of individual molecules through a fluid by mean of the random, individual movements of the molecules. (2) A B B B B (1) n n B B A Figure 3: Schematic diagram of molecular diffusion process If there are greater number of A molecules near point (1) than at (2), then since molecules diffuse randomly in both direction, more A molecules will diffuse from (1) to (2) than from (2) to (1). The net diffusion of A is from high to low concentration regions.

n - The two modes of mass transfer: Molecular diffusion Convective mass transfer

Molecular diffusion The diffusion of molecules when the whole bulk fluid is not moving but stationary. Diffusion of molecules is due to a concentration gradient. The general Fick’s Law Equation for binary mixture of A and B c = total concentration of A and B [kgmol (A + B)/m 3] x. A= mole fraction of A in the mixture of A and B

Example A mixture of He and N 2 gas is contained in a pipe at 298 K and 1 atm total pressure which is constant throughout. At one end of the pipe at point 1 the partial pressure p. A 1 of He is 0. 6 atm and at the other end 0. 2 m p. A 2 = 0. 2 atm. Calculate the flux of He at steady state if DAB of the He-N 2 mixture is 0. 687 x 10 -4 m 2/s.

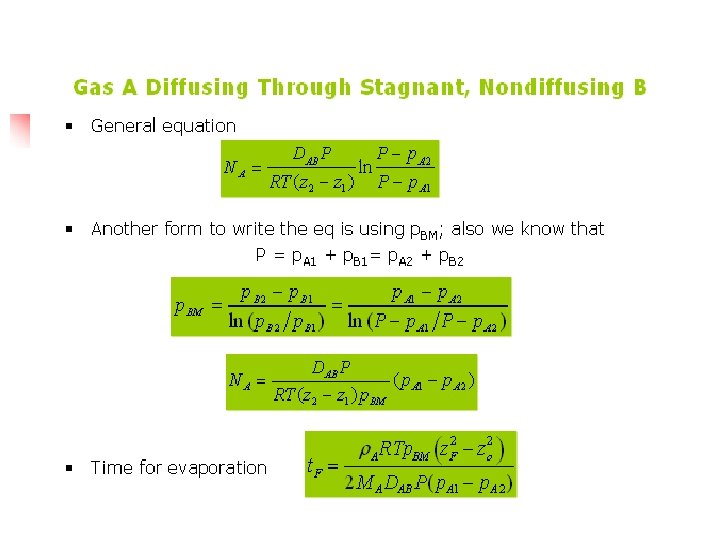
Solution n Since a total pressure P is constant, the c is constant, where c is as follows for a gas according to the perfect gas law: Where n is kg mol A plus B, V is volume in m 3, T is temperature in K, R is 8314. 3 m 3. Pa/kg mol. K or R is 82. 057 x 10 -3 cm 3. atm/g. mol. K, and c is kg mol A plus B/m 3. For steady state the flux J*Az in Eq. (6. 1 -3) is constant. Also DAB for gas is constant. Rearranging Eq. (6. 1 -3) and integrating. (6. 1 -11)

n Also, from the perfect gas law, p. AV=n. ART, and n Substituting Eq. (6. 1 -12) into (6. 1 -11), (6. 1 -13) n This is the final equation to use, which is in a form eqsily used for gases. Partial pressures are p. A 1 = 0. 6 atm = 0. 6 x 1. 01325 x 105 = 6. 04 x 104 Pa and p. A 2 = 0. 2 atm = 0. 2 x 1. 01325 x 105 = 2. 027 x 104 Pa. Then, using SI units,

n n If pressures in atm are used with SI unit, Other driving forces (besides concentration differences) for diffusion also occur because of temperature, pressure, electrical potential, and other gradients.

Convection Mass Transfer n When a fluid flowing outside a solid surface in forced convection motion, rate of convective mass transfer is given by: kc c. L 1 c. Li n - mass transfer coefficient (m/s) - bulk fluid conc. - conc of fluid near the solid surface Kc depend on: 1. 2. 3. system geometry Fluid properties Flow velocity

Principles of Mass Transfer Molecular Diffusion in Gases

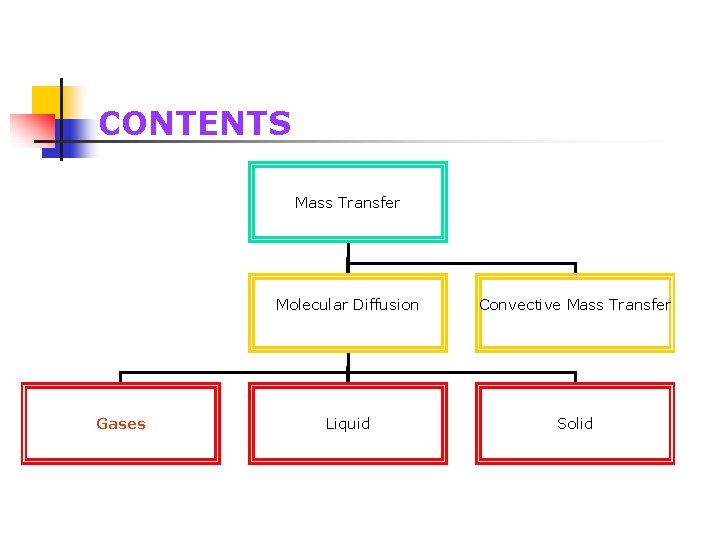
CONTENTS Mass Transfer Gases Molecular Diffusion Convective Mass Transfer Liquid Solid

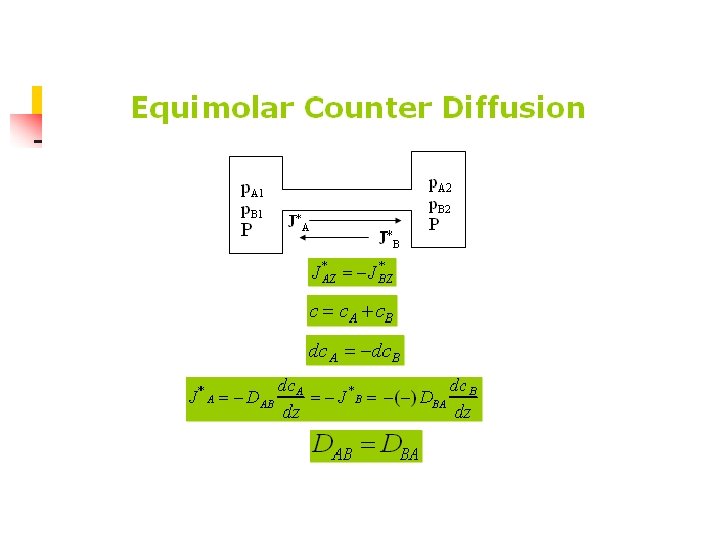
Molecular Diffusion in Gases n Equimolar Counterdiffussion in Gases

n For a binary gas mixture of A and B, the diffusivity coefficient DAB=DBA

Example 6. 2 -1 Ammonia gas (A) is diffusing through a uniform tube 0. 10 m long containing N 2 gas (B) at 1. 0132 x 105 Pa pressure and 298 K. The diagram is similar to Fig. 6. 21. At point 1, p. A 1 = 1. 013 x 104 Pa and at point 2, p. A 2 = 0. 507 x 104 Pa. The diffusivity DAB = 0. 230 x 10 -4 m 2/s. (a) Calculate the flux J*A at steady state (b) Repeat for J*B

Solution n Equation (6. 1 -13) can be used, where P = 1. 0132 x 105 Pa, z 2 -z 1 = 0. 10 m, and T = 298 K. Substituting into Eq. (6. 1 -13) for part (a), Rewriting Eq. (6. 1 -13) for component B for part (b) and noting that p. B 1 = P – p. A 1 = 1. 01325 x 105 – 1. 013 x 104 = 9. 119 x 104 Pa and p. B 2 = P – p. A 2 = 1. 01325 x 105 – 0. 507 x 104 = 9. 625 x 104 Pa. The negative for J*B means the flux goes from point 2 to point 1.

Diffusion of Gases A and B Plus Convection

For equimolar counterdiffussion, NA=-NB , then NA=J*A=-NB=-J*B

Example 6. 2 -2 Water in the bottom of a narrow metal tube is held at a constant temperature of 293 K. The total pressure of air (assumed dry) is 1. 01325 x 105 Pa (1. 0 atm) and the temperature is 293 K (20 °C). Water evaporates and diffuses through the air in the tube, and the diffusion path z 2 -z 1 is 0. 1524 m (0. 5 ft) long. The diagram is similar to Fig. 6. 2 -2 a. Calculate the rate of evaporation at steady state in lb mol/h. ft 2 and kg mol/s. m 2. The diffusivity of water vapor at 293 K and 1 am pressure is 0. 250 x 10 -4 m 2/s. Assume that the system is isothermal. Use SI and English units.

Solution n n The diffusivity is converted to ft 2/h by using the conversion factor: From Appendix A. 2 the vapor pressure of water at 20 °C is 17. 54 mm, or p. A 1 = 17. 54/760 = 0. 0231 atm = 0. 0231(1. 01325 x 105) = 2. 341 x 103 Pa, p. A 2 = 0 (pure air). Since the temperature is 20 °C (68 °F), T = 460 + 68 °R = 293 K. From Appendix A. 1, R = 0. 730 ft 3. atm/lb mol. °R. To calculate the value of p. BM from Eq. (6. 2 -21)

n n Since p. B 1 is close to p. B 2, the linear mean (p. B 1+p. B 2)/2 could be used and would be very close to p. BM. Substituting into Eq. (6. 2 -22) with z 2 -z 1 = 0. 5 ft (0. 1524 m),

Example 6. 2 -4 A sphere of naphthalene having a radius of 2. 0 mm is suspended in a large volume of still air at 318 K and 1. 101325 x 105 Pa (1 atm). The diffusivity of the naphthalene at 318 K is 6. 92 x 10 -6 m 2/s. Calculate the rate of evaporation of naphthalene from the surface.

Solution n n The flow diagram is similar to Fig. 6. 2 -3 a. DAB = 6. 92 x 10 -6 m 2/s, p. A 1 = (0. 555/760)(1. 01325 x 105) = 74. 0 Pa, p. A 2 = 0, r 1 = 2/1000 m, R = 8314 m 3. Pa/kg mol. K, p. B 1 = P-p. A 1 = 1. 01325 x 105 – 74. 0 = 1. 01251 x 105 Pa, p. B 2 = 1. 01325 x 105 – 0. since the values of p. B 1 and p. B 2 are close to each other, Substituting into Eq. (6. 2 -32),

Example 6. 2 -5 Normal butanol (A) is diffusing through air (B) at 1 atm abs. Using the Fuller et al. method, estimate the diffusivity DAB for the following temperatures with the experimental data: (a) For 0 °C. (b) For 25. 9 °C. (c) For 0 °C and 2. 0 atm abs.

Solution n For part (a), P = 1. 00 atm, T = 273 + 0 = 273 K, MA (butanol) = 74. 1, MB (air) = 29. From Table 6. 2 -2, Substituting into Eq. (6. 2 -45), This values deviates +10% from the experimental values of 7. 03 x 10 -6 m 2/s from Table 6. 2 -1

n n For part (b), T = 273 + 25. 9 = 298. 9. Substituting into Eq. (6. 245), DAB= 9. 05 x 10 -6 m 2/s. This values deviates by +4% from the experimental value of 8. 70 x 10 -6 m 2/s For part (c), the total pressure P = 2. 0 atm. Using the value predicted in part (a) and correcting for pressure, DAB = 7. 73 x 10 -6(1. 0/2. 0) = 3. 865 x 10 -6 m 2/s