Introduction to Management Science 8 th Edition by

Introduction to Management Science 8 th Edition by Bernard W. Taylor III Chapter 12 Decision Analysis Chapter 12 - Decision Analysis 1

Chapter Topics Components of Decision Making without Probabilities Decision Making with Probabilities Decision Analysis with Additional Information Utility Chapter 12 - Decision Analysis 2

Decision Analysis Components of Decision Making A state of nature is an actual event that may occur in the future. A payoff table is a means of organizing a decision situation, presenting the payoffs from different decisions given the various states of nature. Table 12. 1 Payoff Table Chapter 12 - Decision Analysis 3

Decision Analysis Decision Making without Probabilities Decision situation: Table 12. 2 Payoff Table for the Real Estate Investments • Decision-Making Criteria: maximax, maximin, minimax regret, Hurwicz, and equal likelihood Chapter 12 - Decision Analysis 4

Decision Making without Probabilities Maximax Criterion In the maximax criterion the decision maker selects the decision that will result in the maximum of maximum payoffs; an optimistic criterion. Table 12. 3 Payoff Table Illustrating a Maximax Decision Chapter 12 - Decision Analysis 5

Decision Making without Probabilities Maximin Criterion In the maximin criterion the decision maker selects the decision that will reflect the maximum of the minimum payoffs; a pessimistic criterion. Table 12. 4 Payoff Table Illustrating a Maximin Decision Chapter 12 - Decision Analysis 6

Decision Making without Probabilities Minimax Regret Criterion Regret is the difference between the payoff from the best decision and all other decision payoffs. The decision maker attempts to avoid regret by selecting the decision alternative that minimizes the maximum regret. Table 12. 6 Regret Table Illustrating the Minimax Regret Decision Chapter 12 - Decision Analysis 7

Decision Making without Probabilities Hurwicz Criterion The Hurwicz criterion is a compromise between the maximax and maximin criterion. A coefficient of optimism, , is a measure of the decision maker’s optimism. The Hurwicz criterion multiplies the best payoff by and the worst payoff by 1 - . , for each decision, and the best result is selected. Decision Apartment building Office building Warehouse Chapter 12 - Decision Analysis Values $50, 000(. 4) + 30, 000(. 6) = 38, 000 $100, 000(. 4) - 40, 000(. 6) = 16, 000 $30, 000(. 4) + 10, 000(. 6) = 18, 000 8

Decision Making without Probabilities Equal Likelihood Criterion The equal likelihood ( or Laplace) criterion multiplies the decision payoff for each state of nature by an equal weight, thus assuming that the states of nature are equally likely to occur. Decision Apartment building Office building Warehouse Chapter 12 - Decision Analysis Values $50, 000(. 5) + 30, 000(. 5) = 40, 000 $100, 000(. 5) - 40, 000(. 5) = 30, 000 $30, 000(. 5) + 10, 000(. 5) = 20, 000 9

Decision Making without Probabilities Summary of Criteria Results A dominant decision is one that has a better payoff than another decision under each state of nature. The appropriate criterion is dependent on the “risk” personality and philosophy of the decision maker. Criterion Decision (Purchase) Maximax Office building Maximin Apartment building Minimax regret Apartment building Hurwicz Apartment building Equal likelihood Apartment building Chapter 12 - Decision Analysis 10

Decision Making without Probabilities Solution with QM for Windows (1 of 3) Exhibit 12. 1 Chapter 12 - Decision Analysis 11

Decision Making without Probabilities Solution with QM for Windows (2 of 3) Exhibit 12. 2 Chapter 12 - Decision Analysis 12

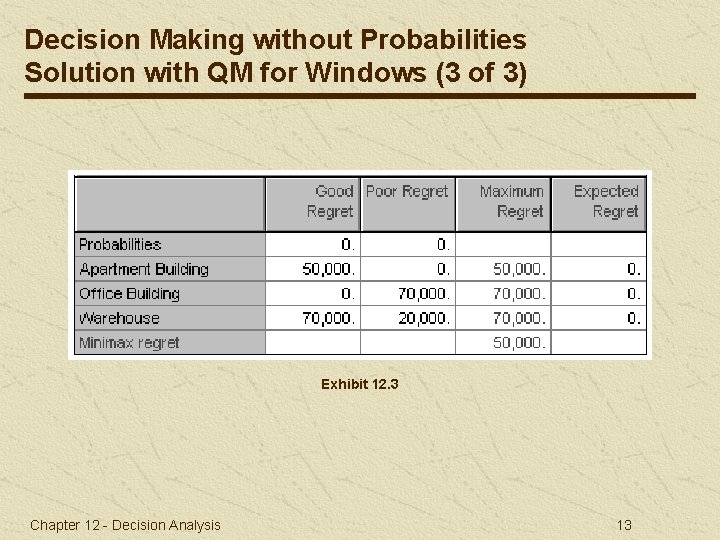
Decision Making without Probabilities Solution with QM for Windows (3 of 3) Exhibit 12. 3 Chapter 12 - Decision Analysis 13

Decision Making with Probabilities Expected Value Expected value is computed by multiplying each decision outcome under each state of nature by the probability of its occurrence. Table 12. 7 Payoff table with Probabilities for States of Nature EV(Apartment) = $50, 000(. 6) + 30, 000(. 4) = 42, 000 EV(Office) = $100, 000(. 6) - 40, 000(. 4) = 44, 000 EV(Warehouse) = $30, 000(. 6) + 10, 000(. 4) = 22, 000 Chapter 12 - Decision Analysis 14

Decision Making with Probabilities Expected Opportunity Loss The expected opportunity loss is the expected value of the regret for each decision. The expected value and expected opportunity loss criterion result in the same decision. Table 12. 8 Regret (Opportunity Loss) Table with Probabilities for States of Nature EOL(Apartment) = $50, 000(. 6) + 0(. 4) = 30, 000 EOL(Office) = $0(. 6) + 70, 000(. 4) = 28, 000 EOL(Warehouse) = $70, 000(. 6) + 20, 000(. 4) = 50, 000 Chapter 12 - Decision Analysis 15

Expected Value Problems Solution with QM for Windows Exhibit 12. 4 Chapter 12 - Decision Analysis 16

Expected Value Problems Solution with Excel and Excel QM (1 of 2) Exhibit 12. 5 Chapter 12 - Decision Analysis 17

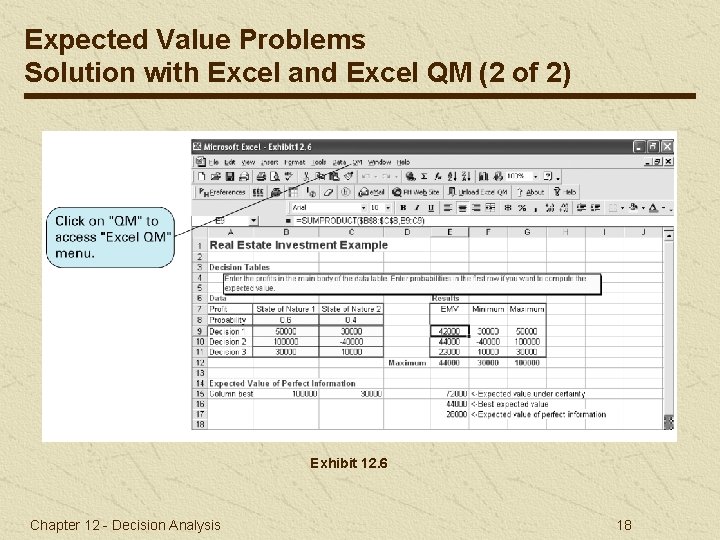
Expected Value Problems Solution with Excel and Excel QM (2 of 2) Exhibit 12. 6 Chapter 12 - Decision Analysis 18

Decision Making with Probabilities Expected Value of Perfect Information The expected value of perfect information (EVPI) is the maximum amount a decision maker would pay for additional information. EVPI equals the expected value given perfect information minus the expected value without perfect information. EVPI equals the expected opportunity loss (EOL) for the best decision. Chapter 12 - Decision Analysis 19

Decision Making with Probabilities EVPI Example (1 of 2) Table 12. 9 Payoff Table with Decisions, Given Perfect Information Chapter 12 - Decision Analysis 20

Decision Making with Probabilities EVPI Example (2 of 2) Decision with perfect information: $100, 000(. 60) + 30, 000(. 40) = $72, 000 Decision without perfect information: EV(office) = $100, 000(. 60) - 40, 000(. 40) = $44, 000 EVPI = $72, 000 - 44, 000 = $28, 000 EOL(office) = $0(. 60) + 70, 000(. 4) = $28, 000 Chapter 12 - Decision Analysis 21

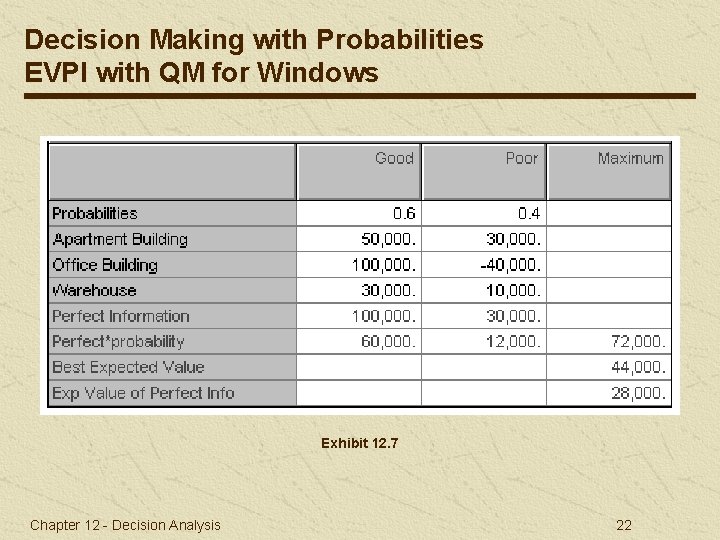
Decision Making with Probabilities EVPI with QM for Windows Exhibit 12. 7 Chapter 12 - Decision Analysis 22

Decision Making with Probabilities Decision Trees (1 of 4) A decision tree is a diagram consisting of decision nodes (represented as squares), probability nodes (circles), and decision alternatives (branches). Table 12. 10 Payoff Table for Real Estate Investment Example Chapter 12 - Decision Analysis 23

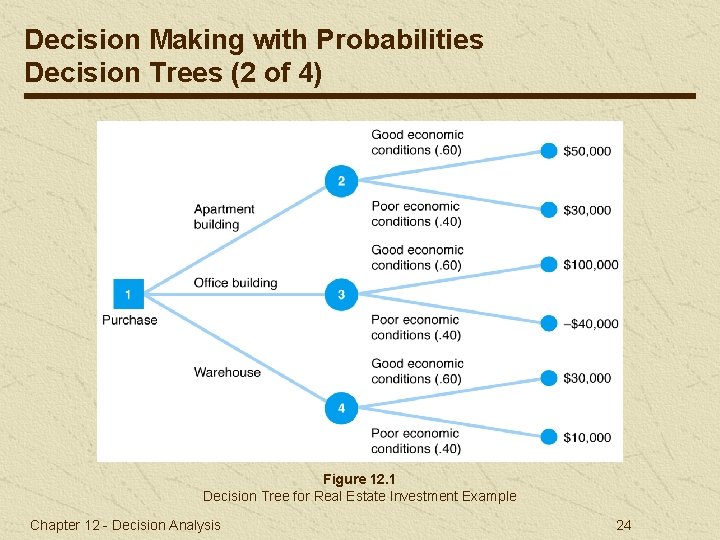
Decision Making with Probabilities Decision Trees (2 of 4) Figure 12. 1 Decision Tree for Real Estate Investment Example Chapter 12 - Decision Analysis 24

Decision Making with Probabilities Decision Trees (3 of 4) The expected value is computed at each probability node: EV(node 2) =. 60($50, 000) +. 40(30, 000) = $42, 000 EV(node 3) =. 60($100, 000) +. 40(-40, 000) = $44, 000 EV(node 4) =. 60($30, 000) +. 40(10, 000) = $22, 000 Branches with the greatest expected value are selected. Chapter 12 - Decision Analysis 25

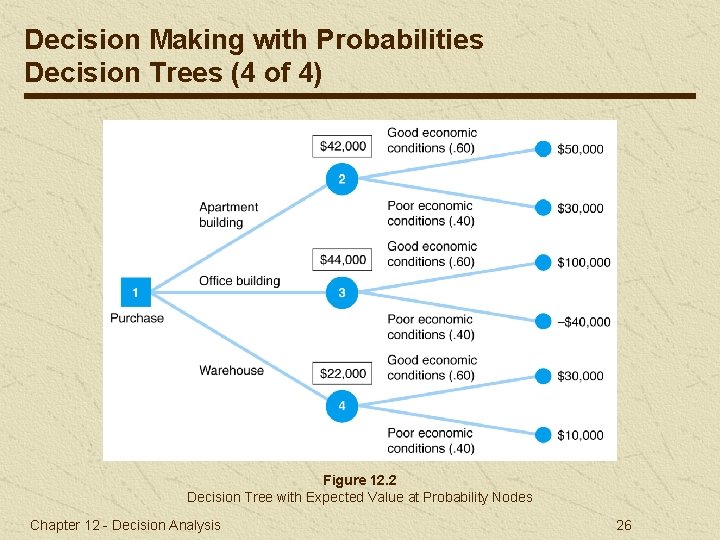
Decision Making with Probabilities Decision Trees (4 of 4) Figure 12. 2 Decision Tree with Expected Value at Probability Nodes Chapter 12 - Decision Analysis 26

Decision Making with Probabilities Decision Trees with QM for Windows Exhibit 12. 8 Chapter 12 - Decision Analysis 27

Decision Making with Probabilities Decision Trees with Excel and Tree. Plan (1 of 4) Exhibit 12. 9 Chapter 12 - Decision Analysis 28

Decision Making with Probabilities Decision Trees with Excel and Tree. Plan (2 of 4) Exhibit 12. 10 Chapter 12 - Decision Analysis 29

Decision Making with Probabilities Decision Trees with Excel and Tree. Plan (3 of 4) Exhibit 12. 11 Chapter 12 - Decision Analysis 30

Decision Making with Probabilities Decision Trees with Excel and Tree. Plan (4 of 4) Exhibit 12. 12 Chapter 12 - Decision Analysis 31

Decision Making with Probabilities Sequential Decision Trees (1 of 4) A sequential decision tree is used to illustrate a situation requiring a series of decisions. Used where a payoff table, limited to a single decision, cannot be used. Real estate investment example modified to encompass a ten -year period in which several decisions must be made: Chapter 12 - Decision Analysis 32

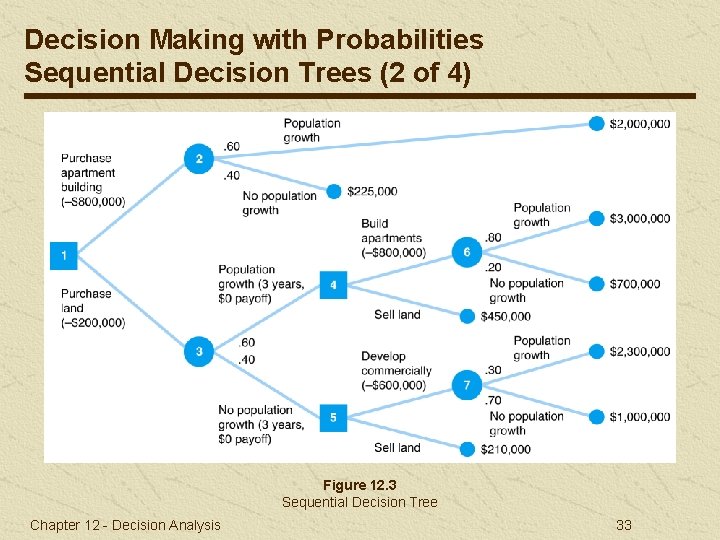
Decision Making with Probabilities Sequential Decision Trees (2 of 4) Figure 12. 3 Sequential Decision Tree Chapter 12 - Decision Analysis 33

Decision Making with Probabilities Sequential Decision Trees (3 of 4) Decision is to purchase land; highest net expected value ($1, 160, 000). Payoff of the decision is $1, 160, 000. Chapter 12 - Decision Analysis 34

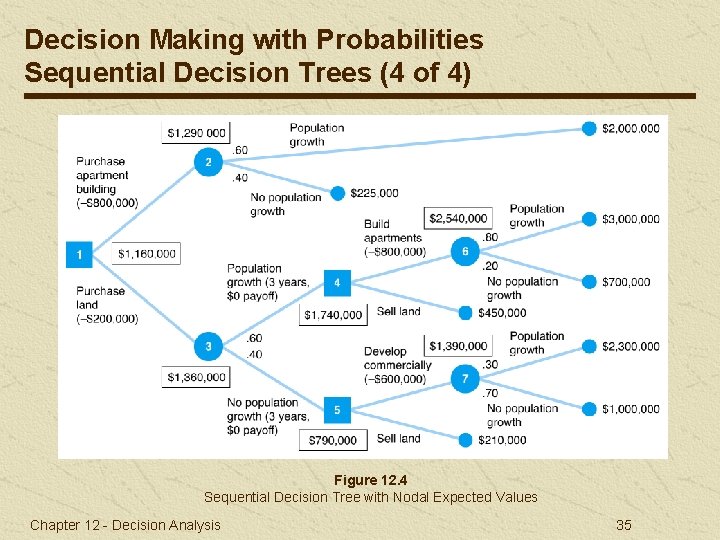
Decision Making with Probabilities Sequential Decision Trees (4 of 4) Figure 12. 4 Sequential Decision Tree with Nodal Expected Values Chapter 12 - Decision Analysis 35

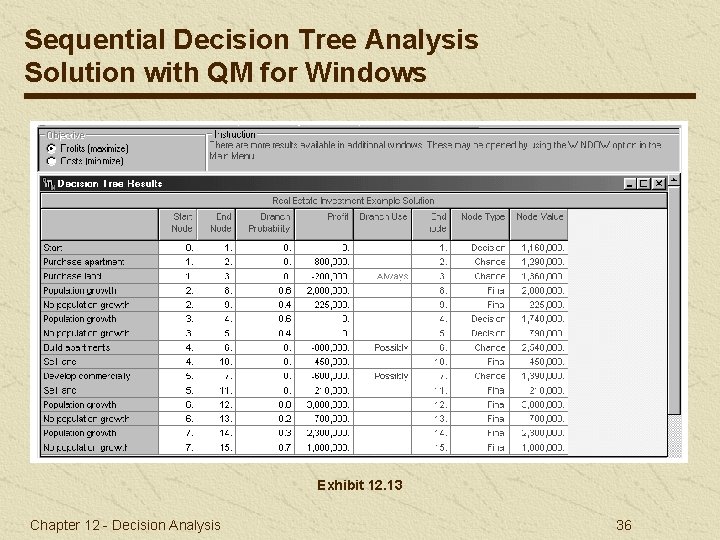
Sequential Decision Tree Analysis Solution with QM for Windows Exhibit 12. 13 Chapter 12 - Decision Analysis 36

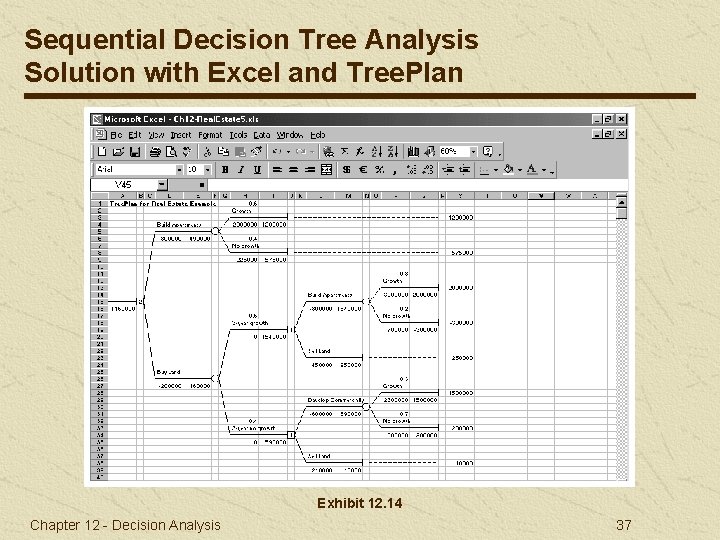
Sequential Decision Tree Analysis Solution with Excel and Tree. Plan Exhibit 12. 14 Chapter 12 - Decision Analysis 37

Decision Analysis with Additional Information Bayesian Analysis (1 of 3) Bayesian analysis uses additional information to alter the marginal probability of the occurrence of an event. In real estate investment example, using expected value criterion, best decision was to purchase office building with expected value of $444, 000, and EVPI of $28, 000. Table 12. 11 Payoff Table for the Real Estate Investment Example Chapter 12 - Decision Analysis 38

Decision Analysis with Additional Information Bayesian Analysis (2 of 3) A conditional probability is the probability that an event will occur given that another event has already occurred. Economic analyst provides additional information for real estate investment decision, forming conditional probabilities: g = good economic conditions p = poor economic conditions P = positive economic report N = negative economic report P(P g) =. 80 P(N G) =. 20 P(P p) =. 10 P(N p) =. 90 Chapter 12 - Decision Analysis 39

Decision Analysis with Additional Information Bayesian Analysis (3 of 3) A posteria probability is the altered marginal probability of an event based on additional information. Prior probabilities for good or poor economic conditions in real estate decision: P(g) =. 60; P(p) =. 40 Posteria probabilities by Bayes’ rule: (g P) = P(P G)P(g)/[P(P g)P(g) + P(P p)P(p)] = (. 80)(. 60)/[(. 80)(. 60) + (. 10)(. 40)] =. 923 Posteria (revised) probabilities for decision: P(g N) =. 250 Chapter 12 - Decision Analysis P(p P) =. 077 P(p N) =. 750 40

Decision Analysis with Additional Information Decision Trees with Posterior Probabilities (1 of 4) Decision tree with posterior probabilities differ from earlier versions in that: Two new branches at beginning of tree represent report outcomes. Probabilities of each state of nature are posterior probabilities from Bayes’ rule. Chapter 12 - Decision Analysis 41

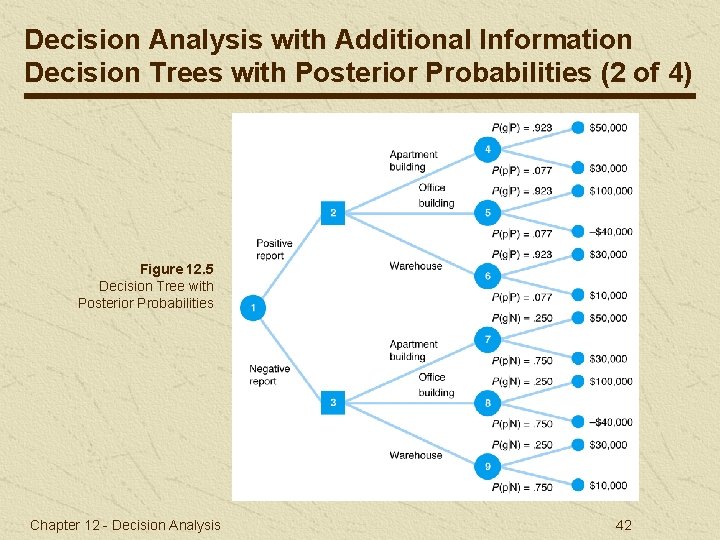
Decision Analysis with Additional Information Decision Trees with Posterior Probabilities (2 of 4) Figure 12. 5 Decision Tree with Posterior Probabilities Chapter 12 - Decision Analysis 42

Decision Analysis with Additional Information Decision Trees with Posterior Probabilities (3 of 4) EV (apartment building) = $50, 000(. 923) + 30, 000(. 077) = $48, 460 EV (strategy) = $89, 220(. 52) + 35, 000(. 48) = $63, 194 Chapter 12 - Decision Analysis 43

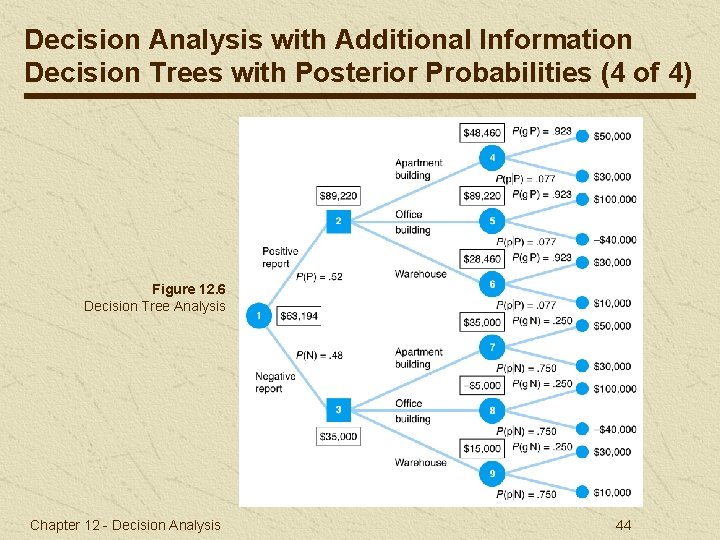
Decision Analysis with Additional Information Decision Trees with Posterior Probabilities (4 of 4) Figure 12. 6 Decision Tree Analysis Chapter 12 - Decision Analysis 44

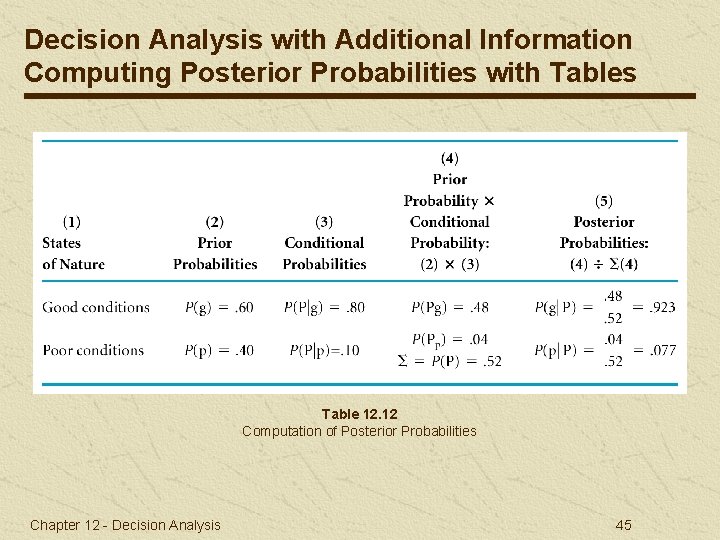
Decision Analysis with Additional Information Computing Posterior Probabilities with Tables Table 12. 12 Computation of Posterior Probabilities Chapter 12 - Decision Analysis 45

Decision Analysis with Additional Information Expected Value of Sample Information The expected value of sample information (EVSI) is the difference between the expected value with and without information: For example problem, EVSI = $63, 194 - 44, 000 = $19, 194 The efficiency of sample information is the ratio of the expected value of sample information to the expected value of perfect information: efficiency = EVSI /EVPI = $19, 194/ 28, 000 =. 68 Chapter 12 - Decision Analysis 46

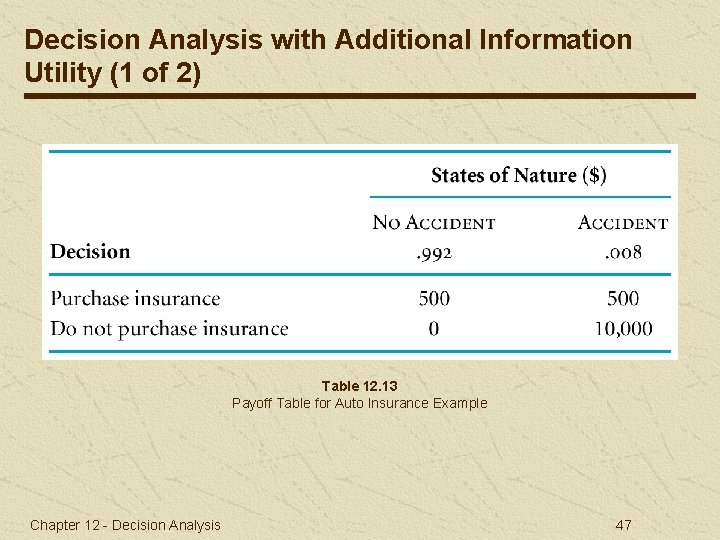
Decision Analysis with Additional Information Utility (1 of 2) Table 12. 13 Payoff Table for Auto Insurance Example Chapter 12 - Decision Analysis 47

Decision Analysis with Additional Information Utility (2 of 2) Expected Cost (insurance) =. 992($500) +. 008(500) = $500 Expected Cost (no insurance) =. 992($0) +. 008(10, 000) = $80 Decision should be do not purchase insurance, but people almost always do purchase insurance. Utility is a measure of personal satisfaction derived from money. Utiles are units of subjective measures of utility. Risk averters forgo a high expected value to avoid a lowprobability disaster. Risk takers take a chance for a bonanza on a very lowprobability event in lieu of a sure thing. Chapter 12 - Decision Analysis 48

Decision Analysis Example Problem Solution (1 of 9) Chapter 12 - Decision Analysis 49

Decision Analysis Example Problem Solution (2 of 9) a. Determine the best decision without probabilities using the 5 criteria of the chapter. b. Determine best decision with probabilities assuming. 70 probability of good conditions, . 30 of poor conditions. Use expected value and expected opportunity loss criteria. c. Compute expected value of perfect information. d. Develop a decision tree with expected value at the nodes. e. Given following, P(P g) =. 70, P(N g) =. 30, P(P p) = 20, P(N p) =. 80, determine posteria probabilities using Bayes’ rule. f. Perform a decision tree analysis using the posterior probability obtained in part e. Chapter 12 - Decision Analysis 50

Decision Analysis Example Problem Solution (3 of 9) Step 1 (part a): Determine decisions without probabilities. Maximax Decision: Maintain status quo Decisions Maximum Payoffs Expand Status quo Sell $800, 000 1, 300, 000 (maximum) 320, 000 Maximin Decision: Expand Decisions Minimum Payoffs Expand Status quo Sell $500, 000 (maximum) -150, 000 320, 000 Chapter 12 - Decision Analysis 51

Decision Analysis Example Problem Solution (4 of 9) Minimax Regret Decision: Expand Decisions Maximum Regrets Expand $500, 000 (minimum) Status quo 650, 000 Sell 980, 000 Hurwicz ( =. 3) Decision: Expand $800, 000(. 3) + 500, 000(. 7) = $590, 000 Status quo $1, 300, 000(. 3) - 150, 000(. 7) = $285, 000 Sell $320, 000(. 3) + 320, 000(. 7) = $320, 000 Chapter 12 - Decision Analysis 52

Decision Analysis Example Problem Solution (5 of 9) Equal Likelihood Decision: Expand Status quo $800, 000(. 5) + 500, 000(. 5) = $650, 000 $1, 300, 000(. 5) - 150, 000(. 5) = $575, 000 Sell $320, 000(. 5) + 320, 000(. 5) = $320, 000 Step 2 (part b): Determine Decisions with EV and EOL. Expected value decision: Maintain status quo Expand Status quo $800, 000(. 7) + 500, 000(. 3) = $710, 000 $1, 300, 000(. 7) - 150, 000(. 3) = $865, 000 Sell Chapter 12 - Decision Analysis $320, 000(. 7) + 320, 000(. 3) = $320, 000 53

Decision Analysis Example Problem Solution (6 of 9) Expected opportunity loss decision: Maintain status quo Expand Status quo Sell $500, 000(. 7) + 0(. 3) = $350, 000 0(. 7) + 650, 000(. 3) = $195, 000 $980, 000(. 7) + 180, 000(. 3) = $740, 000 Step 3 (part c): Compute EVPI. EV given perfect information = 1, 300, 000(. 7) + 500, 000(. 3) = $1, 060, 000 EV without perfect information = $1, 300, 000(. 7) 150, 000(. 3) = $865, 000 EVPI = $1. 060, 000 - 865, 000 = $195, 000 Chapter 12 - Decision Analysis 54

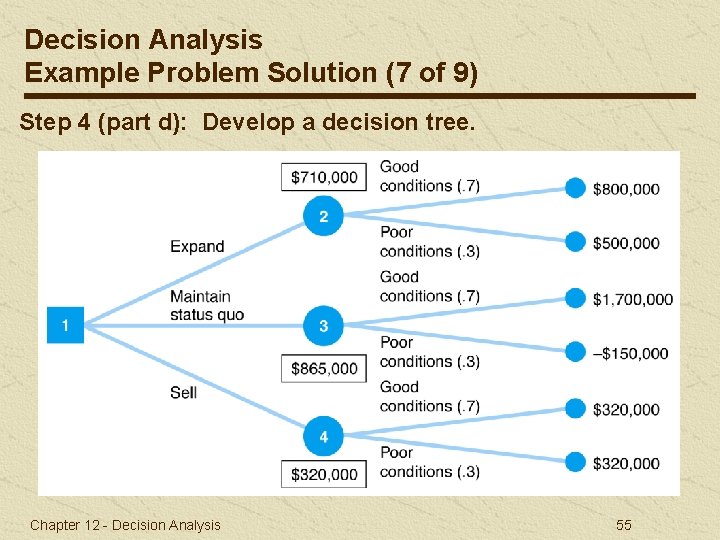
Decision Analysis Example Problem Solution (7 of 9) Step 4 (part d): Develop a decision tree. Chapter 12 - Decision Analysis 55

Decision Analysis Example Problem Solution (8 of 9) Step 5 (part e): Determine posterior probabilities. P(g P) = P(P G)P(g)/[P(P g)P(g) + P(P p)P(p)] = (. 70)/[(. 70) + (. 20)(. 30)] =. 891 P(p P) =. 109 P(g N) = P(N G)P(g)/[P(N g)P(g) + P(N p)P(p)] = (. 30)(. 70)/[(. 30)(. 70) + (. 80)(. 30)] =. 467 P(p N) =. 533 Chapter 12 - Decision Analysis 56

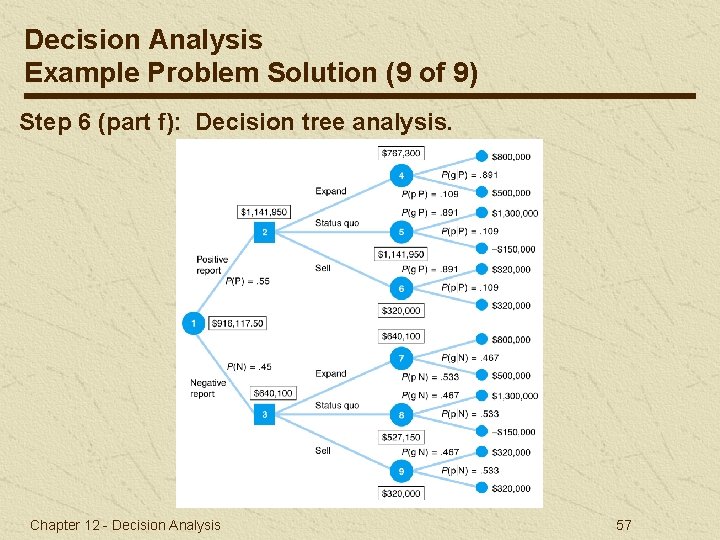
Decision Analysis Example Problem Solution (9 of 9) Step 6 (part f): Decision tree analysis. Chapter 12 - Decision Analysis 57