Introduction to Management Science 8 th Edition by

Introduction to Management Science 8 th Edition by Bernard W. Taylor III Chapter 6 Linear Programming: Model Formulation and Graphical Solution Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 1

Chapter Topics Model Formulation A Maximization Model Example Graphical Solutions of Linear Programming Models A Minimization Model Example Irregular Types of Linear Programming Models Characteristics of Linear Programming Problems Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 2

Linear Programming An Overview Objectives of business firms frequently include maximizing profit or minimizing costs. Linear programming is an analysis technique in which linear algebraic relationships represent a firm’s decisions given a business objective and resource constraints. Steps in application: Identify problem as solvable by linear programming. Formulate a mathematical model of the unstructured problem. Solve the model. Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 3

Model Components and Formulation Decision variables - mathematical symbols representing levels of activity of a firm. Objective function - a linear mathematical relationship describing an objective of the firm, in terms of decision variables, that is maximized or minimized Constraints - restrictions placed on the firm by the operating environment stated in linear relationships of the decision variables. Parameters - numerical coefficients and constants used in the objective function and constraint equations. Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 4

Problem Definition A Maximization Model Example (1 of 2) Product mix problem - Beaver Creek Pottery Company How many bowls and mugs should be produced to maximize profits given labor and materials constraints? Product resource requirements and unit profit: Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 5

Problem Definition A Maximization Model Example (2 of 3) Resource Availability: 40 hrs of labor per day 120 lbs of clay Decision Variables: x 1 = number of bowls to produce per day x 2 = number of mugs to produce per day Objective Function: Maximize Z = $40 x 1 + $50 x 2 Where Z = profit per day Resource Constraints: 1 x 1 + 2 x 2 40 hours of labor 4 x 1 + 3 x 2 120 pounds of clay Non-Negativity Constraints: x 1 0; x 2 0 Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 6

Problem Definition A Maximization Model Example (3 of 3) Complete Linear Programming Model: Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 7

Feasible Solutions A feasible solution does not violate any of the constraints: Example x 1 = 5 bowls x 2 = 10 mugs Z = $40 x 1 + $50 x 2 = $700 Labor constraint check: 1(5) + 2(10) = 25 < 40 hours, within constraint Clay constraint check: 4(5) + 3(10) = 50 < 120 pounds, within constraint Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 8

Infeasible Solutions An infeasible solution violates at least one of the constraints: Example x 1 = 10 bowls x 2 = 20 mugs Z = $1400 Labor constraint check: 1(10) + 2(20) = 50 > 40 hours, violates constraint Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 9

Graphical Solution of Linear Programming Models Graphical solution is limited to linear programming models containing only two decision variables (can be used with three variables but only with great difficulty). Graphical methods provide visualization of how a solution for a linear programming problem is obtained. Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 10

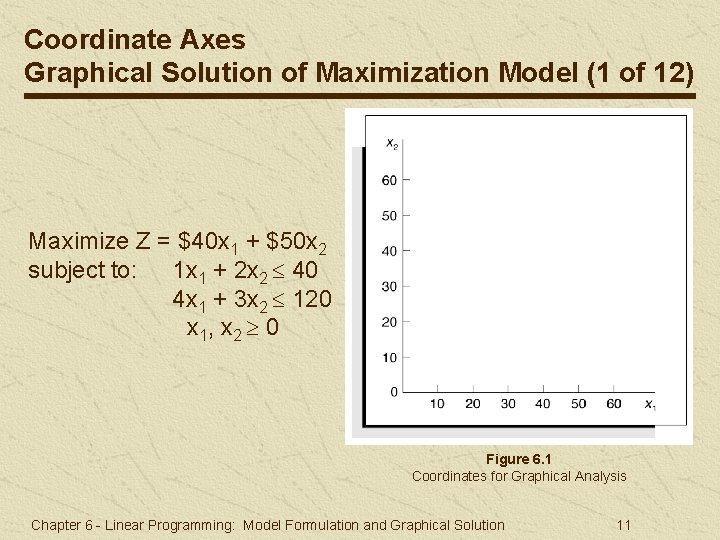
Coordinate Axes Graphical Solution of Maximization Model (1 of 12) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Figure 6. 1 Coordinates for Graphical Analysis Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 11

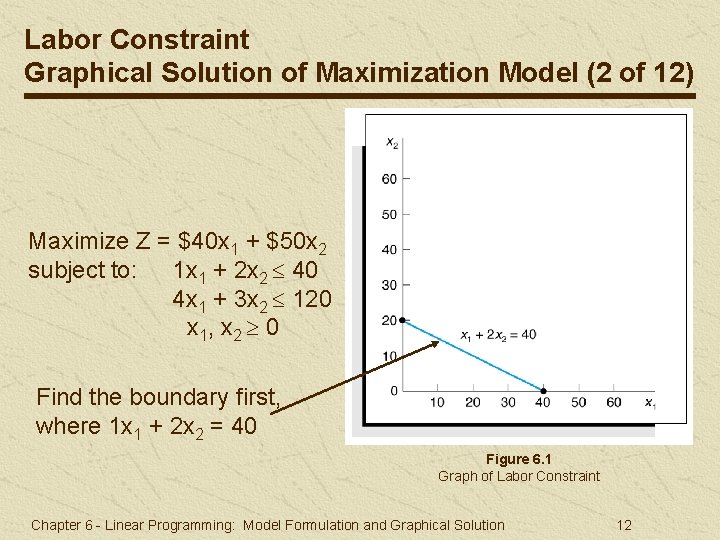
Labor Constraint Graphical Solution of Maximization Model (2 of 12) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Find the boundary first, where 1 x 1 + 2 x 2 = 40 Figure 6. 1 Graph of Labor Constraint Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 12

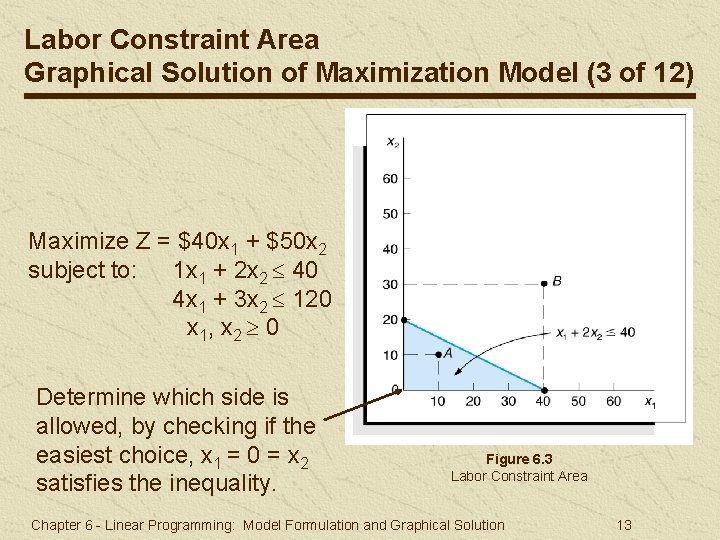
Labor Constraint Area Graphical Solution of Maximization Model (3 of 12) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Determine which side is allowed, by checking if the easiest choice, x 1 = 0 = x 2 satisfies the inequality. Figure 6. 3 Labor Constraint Area Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 13

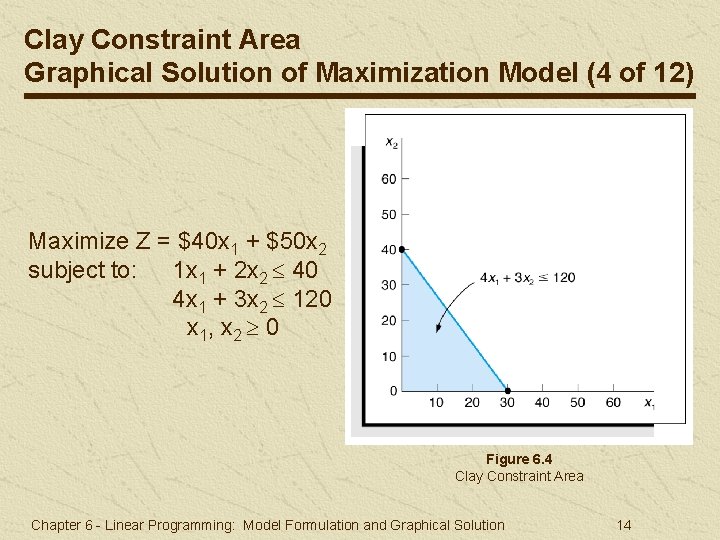
Clay Constraint Area Graphical Solution of Maximization Model (4 of 12) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Figure 6. 4 Clay Constraint Area Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 14

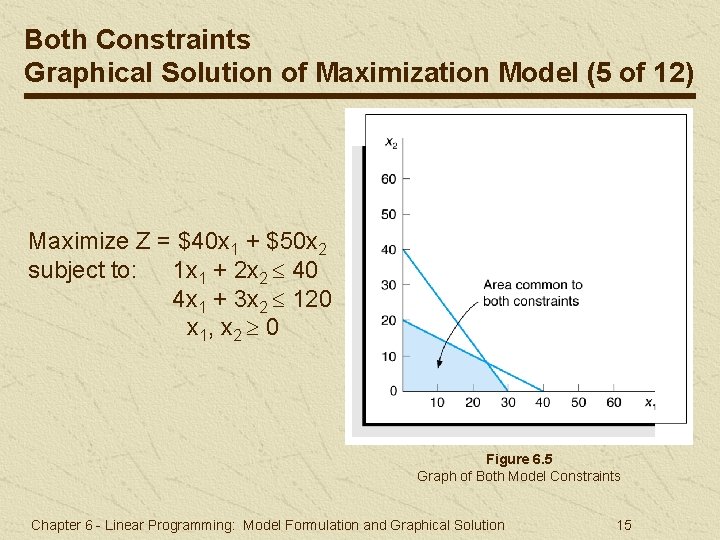
Both Constraints Graphical Solution of Maximization Model (5 of 12) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Figure 6. 5 Graph of Both Model Constraints Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 15

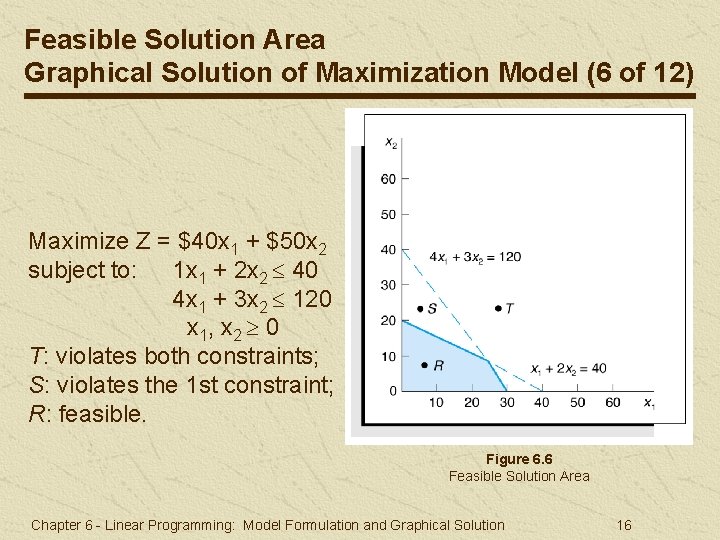
Feasible Solution Area Graphical Solution of Maximization Model (6 of 12) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 T: violates both constraints; S: violates the 1 st constraint; R: feasible. Figure 6. 6 Feasible Solution Area Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 16

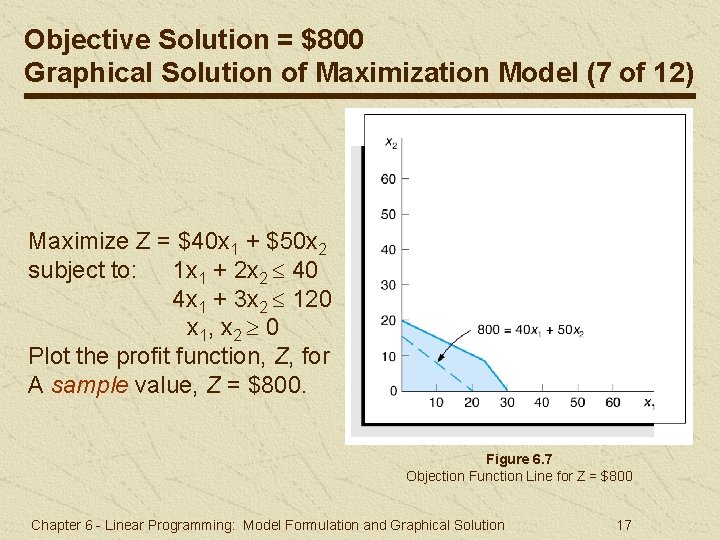
Objective Solution = $800 Graphical Solution of Maximization Model (7 of 12) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Plot the profit function, Z, for A sample value, Z = $800. Figure 6. 7 Objection Function Line for Z = $800 Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 17

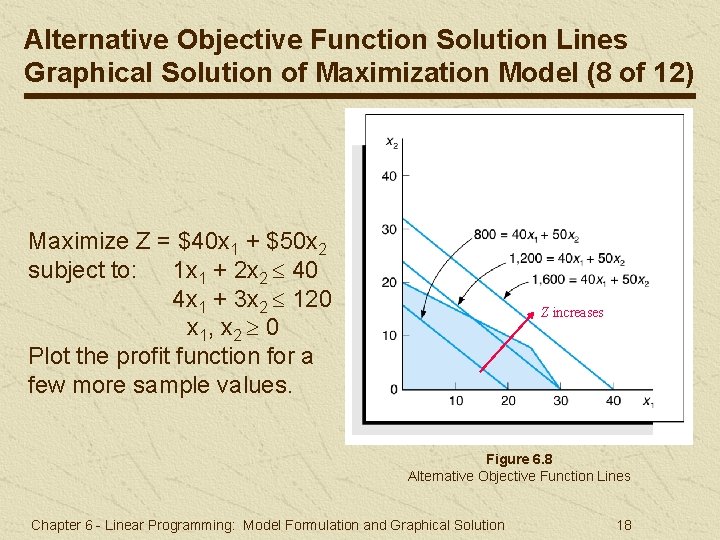
Alternative Objective Function Solution Lines Graphical Solution of Maximization Model (8 of 12) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Plot the profit function for a few more sample values. Z increases Figure 6. 8 Alternative Objective Function Lines Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 18

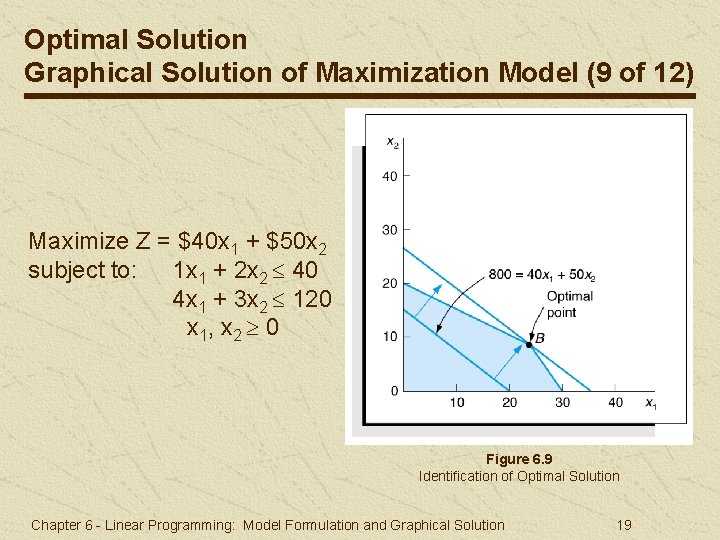
Optimal Solution Graphical Solution of Maximization Model (9 of 12) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Figure 6. 9 Identification of Optimal Solution Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 19

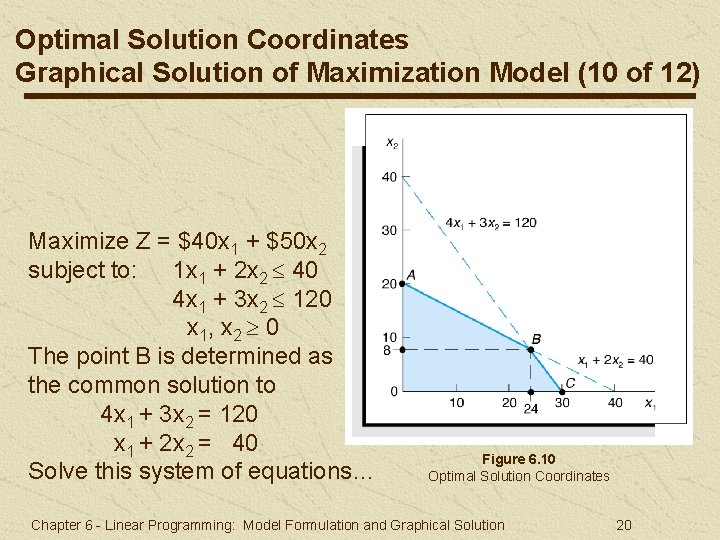
Optimal Solution Coordinates Graphical Solution of Maximization Model (10 of 12) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 The point B is determined as the common solution to 4 x 1 + 3 x 2 = 120 x 1 + 2 x 2 = 40 Solve this system of equations… Figure 6. 10 Optimal Solution Coordinates Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 20

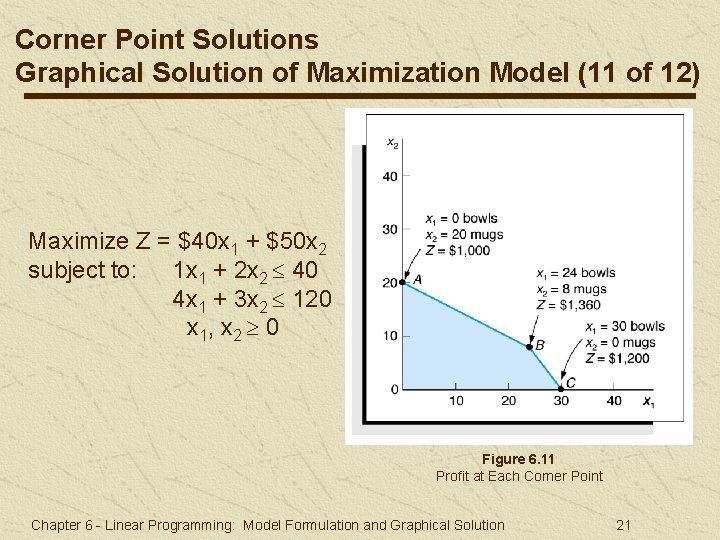
Corner Point Solutions Graphical Solution of Maximization Model (11 of 12) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Figure 6. 11 Profit at Each Corner Point Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 21

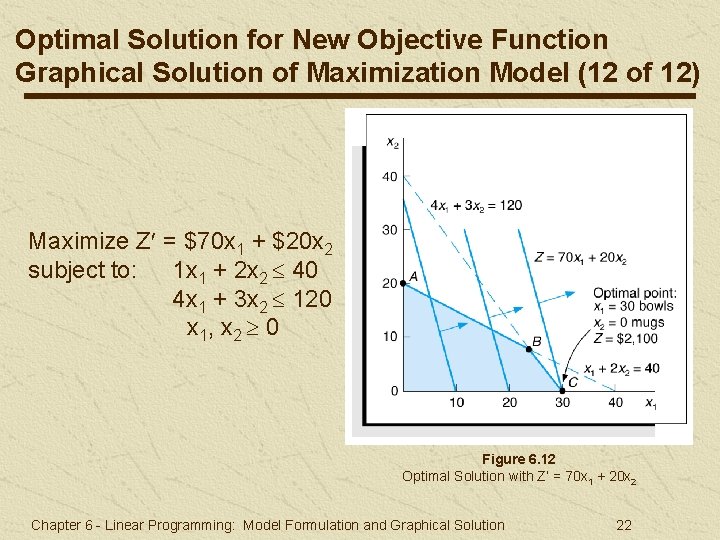
Optimal Solution for New Objective Function Graphical Solution of Maximization Model (12 of 12) Maximize Z = $70 x 1 + $20 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Figure 6. 12 Optimal Solution with Z’ = 70 x 1 + 20 x 2 Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 22

Slack Variables Standard form requires that all constraints be in the form of equations. A slack variable is added to an inequality (≤ or ≥) constraint to convert it to an equation (=). A slack variable represents unused resources. A slack variable contributes nothing to the objective function (total profit, cost, etc. ) value. Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 23

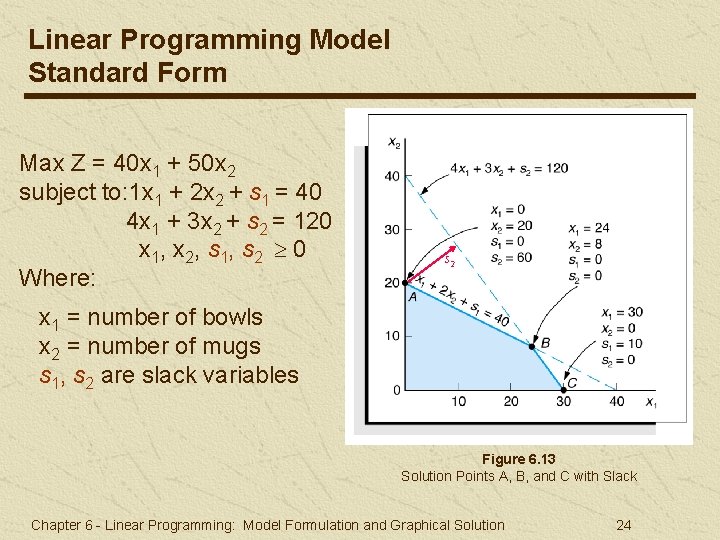
Linear Programming Model Standard Form Max Z = 40 x 1 + 50 x 2 subject to: 1 x 1 + 2 x 2 + s 1 = 40 4 x 1 + 3 x 2 + s 2 = 120 x 1, x 2, s 1, s 2 0 Where: s 2 x 1 = number of bowls x 2 = number of mugs s 1, s 2 are slack variables Figure 6. 13 Solution Points A, B, and C with Slack Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 24

Problem Definition A Minimization Model Example (1 of 7) Two brands of fertilizer available - Super-Gro, Crop-Quick. Field requires at least 16 pounds of nitrogen and 24 pounds of phosphate. Super-Gro costs $6 per bag, Crop-Quick $3 per bag. Problem: How much of each brand to purchase to minimize total cost of fertilizer given following data ? Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 25

Problem Definition A Minimization Model Example (2 of 7) Decision Variables: x 1 = bags of Super-Gro x 2 = bags of Crop-Quick The Objective Function: Minimize Z = $6 x 1 + 3 x 2 Where: $6 x 1 = cost of bags of Super-Gro $3 x 2 = cost of bags of Crop-Quick Model Constraints: 2 x 1 + 4 x 2 16 lb (nitrogen constraint) 4 x 1 + 3 x 2 24 lb (phosphate constraint) x 1, x 2 0 (non-negativity constraint) Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 26

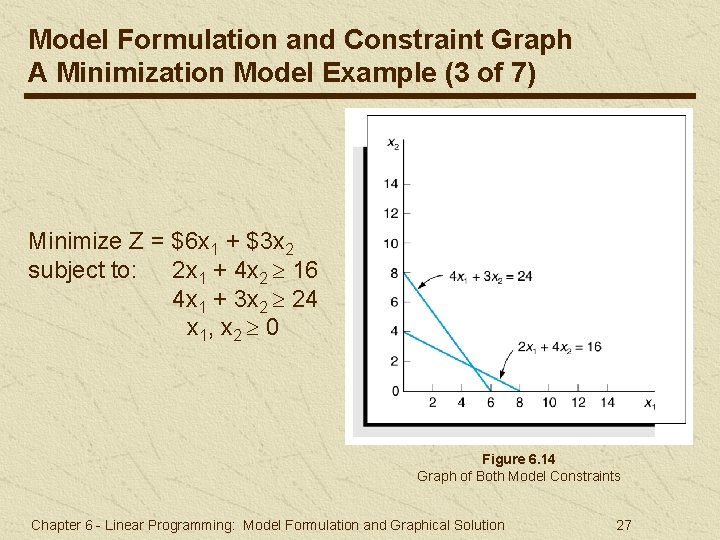
Model Formulation and Constraint Graph A Minimization Model Example (3 of 7) Minimize Z = $6 x 1 + $3 x 2 subject to: 2 x 1 + 4 x 2 16 4 x 1 + 3 x 2 24 x 1, x 2 0 Figure 6. 14 Graph of Both Model Constraints Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 27

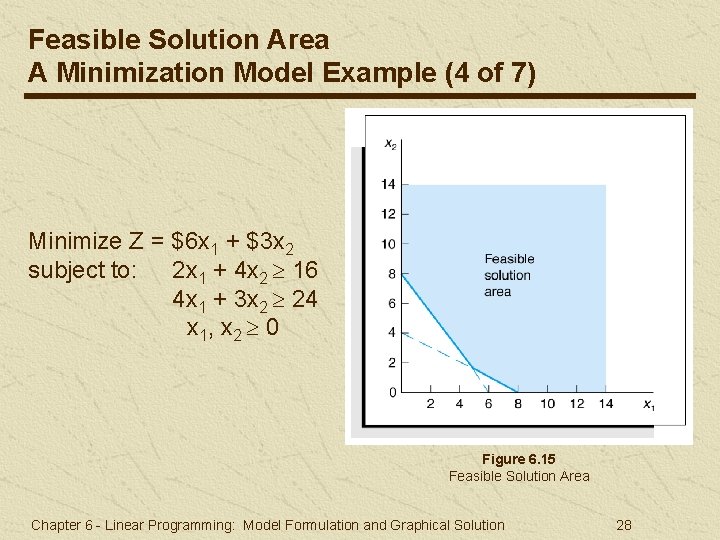
Feasible Solution Area A Minimization Model Example (4 of 7) Minimize Z = $6 x 1 + $3 x 2 subject to: 2 x 1 + 4 x 2 16 4 x 1 + 3 x 2 24 x 1, x 2 0 Figure 6. 15 Feasible Solution Area Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 28

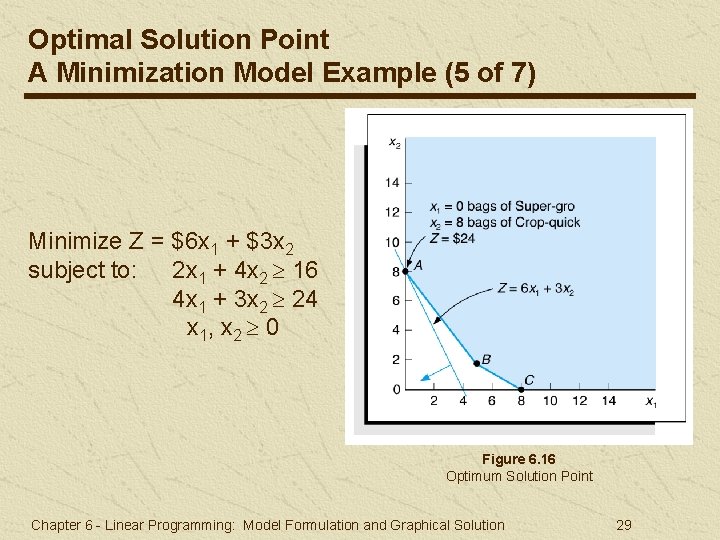
Optimal Solution Point A Minimization Model Example (5 of 7) Minimize Z = $6 x 1 + $3 x 2 subject to: 2 x 1 + 4 x 2 16 4 x 1 + 3 x 2 24 x 1, x 2 0 Figure 6. 16 Optimum Solution Point Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 29

Surplus Variables A Minimization Model Example (6 of 7) A surplus variable is subtracted from an inequality (≥ or ≤) constraint to convert it to an equation (=). A surplus variable represents an excess above a constraint requirement level. Surplus variables contribute nothing to the calculated value of the objective function. Subtracting slack variables in the farmer problem constraints: 2 x 1 + 4 x 2 - s 1 = 16 (nitrogen) 4 x 1 + 3 x 2 - s 2 = 24 (phosphate) Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 30

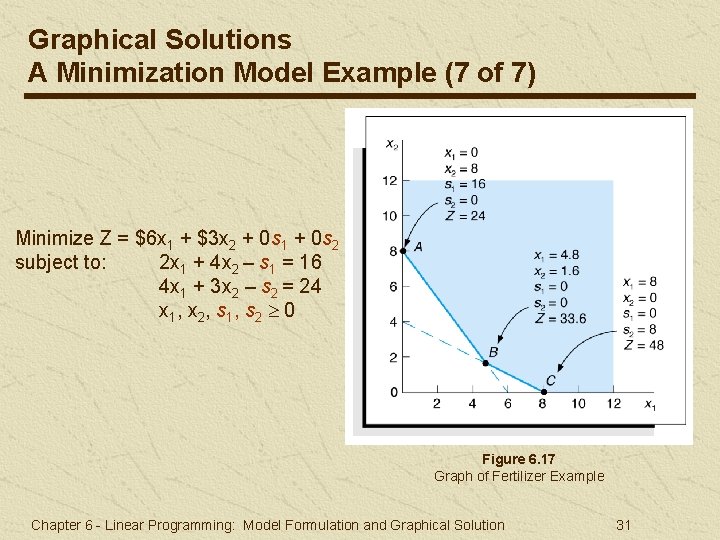
Graphical Solutions A Minimization Model Example (7 of 7) Minimize Z = $6 x 1 + $3 x 2 + 0 s 1 + 0 s 2 subject to: 2 x 1 + 4 x 2 – s 1 = 16 4 x 1 + 3 x 2 – s 2 = 24 x 1, x 2, s 1, s 2 0 Figure 6. 17 Graph of Fertilizer Example Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 31

Irregular Types of Linear Programming Problems For some linear programming models, the general rules do not apply. Special types of problems include those with: Multiple optimal solutions Infeasible solutions Unbounded solutions Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 32

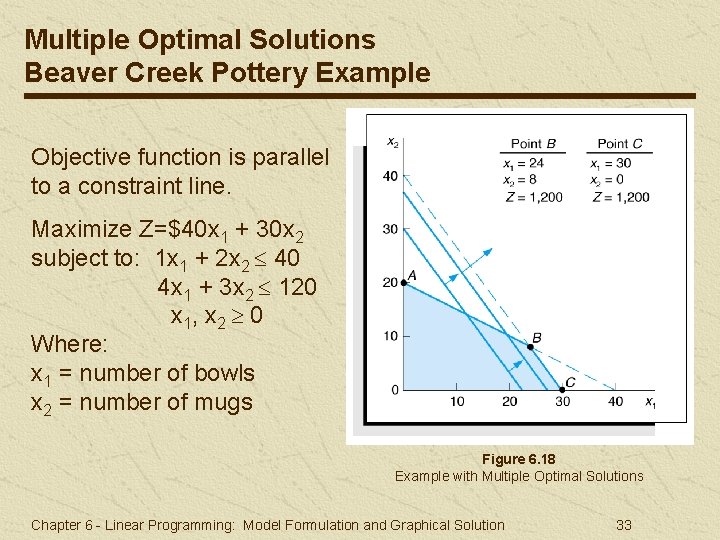
Multiple Optimal Solutions Beaver Creek Pottery Example Objective function is parallel to a constraint line. Maximize Z=$40 x 1 + 30 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Where: x 1 = number of bowls x 2 = number of mugs Figure 6. 18 Example with Multiple Optimal Solutions Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 33

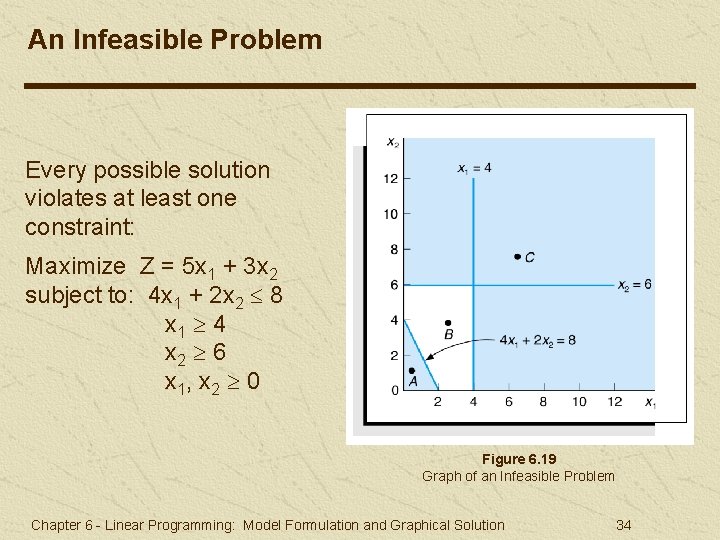
An Infeasible Problem Every possible solution violates at least one constraint: Maximize Z = 5 x 1 + 3 x 2 subject to: 4 x 1 + 2 x 2 8 x 1 4 x 2 6 x 1, x 2 0 Figure 6. 19 Graph of an Infeasible Problem Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 34

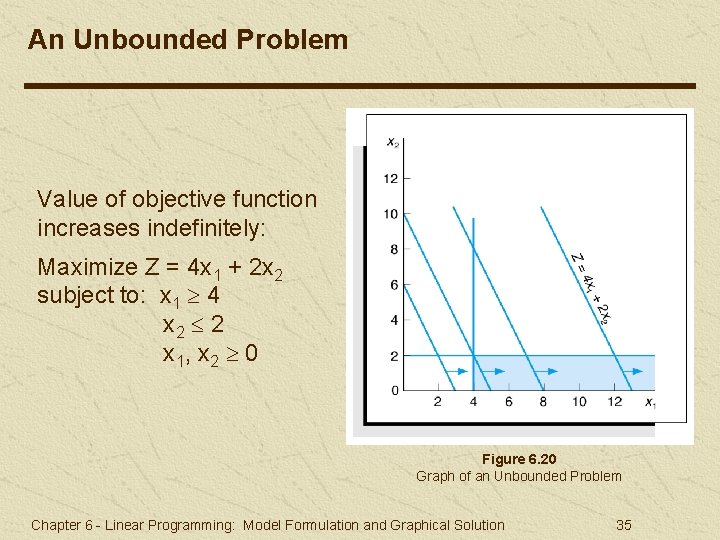
An Unbounded Problem Value of objective function increases indefinitely: Maximize Z = 4 x 1 + 2 x 2 subject to: x 1 4 x 2 2 x 1, x 2 0 Figure 6. 20 Graph of an Unbounded Problem Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 35

Characteristics of Linear Programming Problems A linear programming problem requires a decision—a choice amongst alternative courses of action. The decision is represented in the model by decision variables, of which any mix represents a choice. The problem encompasses a goal, expressed as an objective function, that the decision maker wants to achieve (optimize = minimize or maximize, as appropriate). Constraints exist that limit the extent of achievement of the objective. The objective and constraints must be definable by linear mathematical functional relationships. Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 36

Properties of Linear Programming Models Proportionality - The rate of change (slope) of the objective function and constraint equations is constant. Additivity - Terms in the objective function and constraint equations must be additive. Divisibility -Decision variables can take on any fractional value and are therefore continuous as opposed to integer in nature. Certainty - Values of all the model parameters are assumed to be known with certainty (non-probabilistic). Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 37

Problem Statement Example Problem No. 1 (1 of 4) Hot dog mixture in 1000 -pound batches. Two ingredients, chicken ($3/lb) and beef ($5/lb). Recipe requirements: at least 500 pounds of chicken at least 200 pounds of beef Ratio of chicken to beef must be at least 2 to 1. Determine optimal mixture of ingredients that will minimize costs. Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 38

Solution Example Problem No. 1 (2 of 4) Step 1: Identify decision variables. x 1 = lb of chicken x 2 = lb of beef Step 2: Formulate the objective function. Minimize Z = $3 x 1 + $5 x 2 where Z = cost per 1, 000 -lb batch $3 x 1 = cost of chicken $5 x 2 = cost of beef Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 39

Solution Example Problem No. 1 (3 of 4) Step 3: Establish Model Constraints x 1 + x 2 = 1, 000 lb x 1 500 lb of chicken x 2 200 lb of beef x 1/x 2 2/1, or x 1 2 x 2, or x 1 - 2 x 2 0 x 1, x 2 0 The Model: Minimize Z = $3 x 1 + 5 x 2 subject to: x 1 + x 2 = 1, 000 lb x 1 500 x 2 200 x 1 - 2 x 2 0 x 1, x 2 0 Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 40

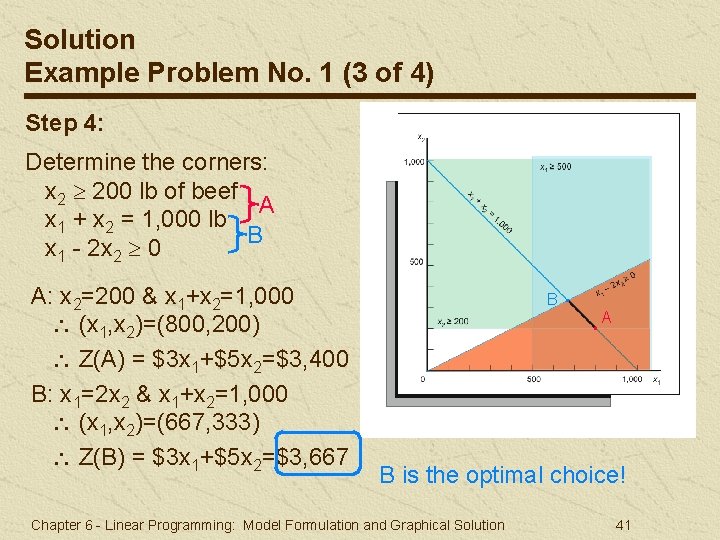
Solution Example Problem No. 1 (3 of 4) Step 4: Determine the corners: x 2 200 lb of beef A x 1 + x 2 = 1, 000 lb B x 1 - 2 x 2 0 A: x 2=200 & x 1+x 2=1, 000 (x 1, x 2)=(800, 200) Z(A) = $3 x 1+$5 x 2=$3, 400 B: x 1=2 x 2 & x 1+x 2=1, 000 (x 1, x 2)=(667, 333) Z(B) = $3 x 1+$5 x 2=$3, 667 B . . A B is the optimal choice! Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 41

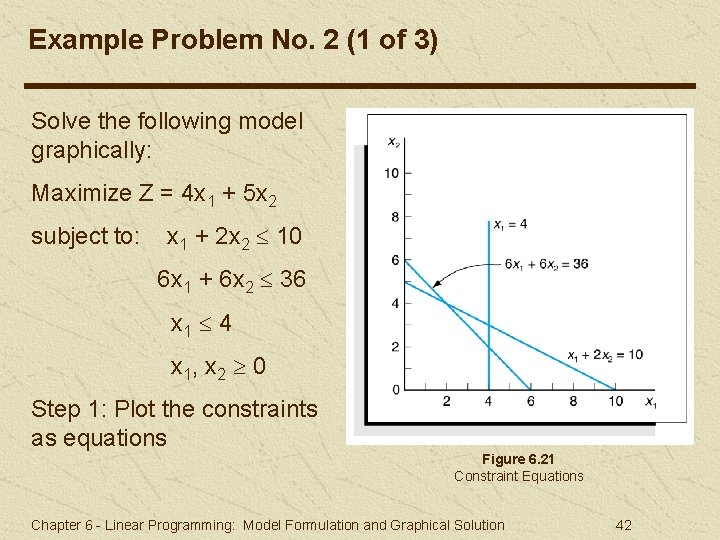
Example Problem No. 2 (1 of 3) Solve the following model graphically: Maximize Z = 4 x 1 + 5 x 2 subject to: x 1 + 2 x 2 10 6 x 1 + 6 x 2 36 x 1 4 x 1, x 2 0 Step 1: Plot the constraints as equations Figure 6. 21 Constraint Equations Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 42

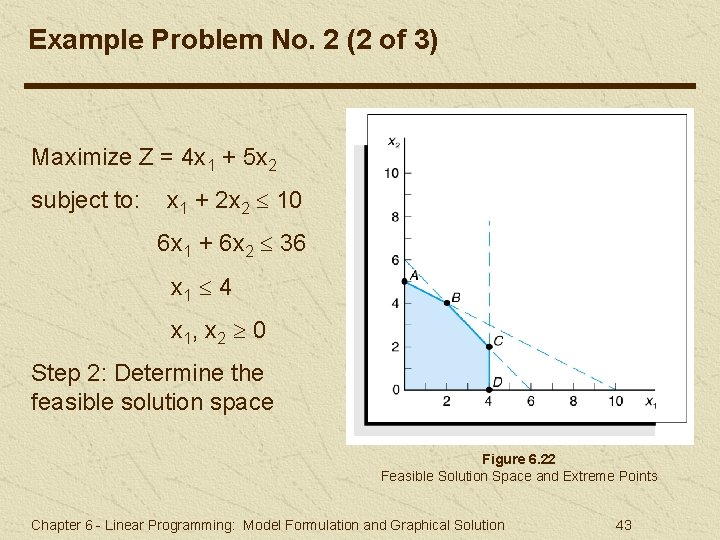
Example Problem No. 2 (2 of 3) Maximize Z = 4 x 1 + 5 x 2 subject to: x 1 + 2 x 2 10 6 x 1 + 6 x 2 36 x 1 4 x 1, x 2 0 Step 2: Determine the feasible solution space Figure 6. 22 Feasible Solution Space and Extreme Points Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 43

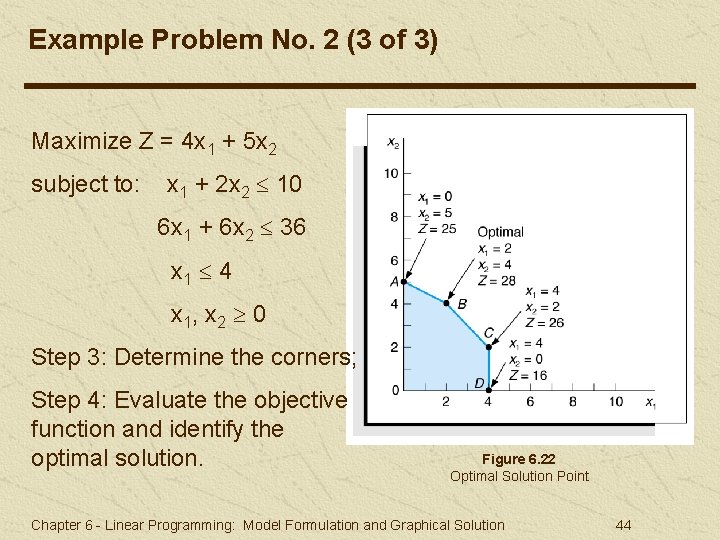
Example Problem No. 2 (3 of 3) Maximize Z = 4 x 1 + 5 x 2 subject to: x 1 + 2 x 2 10 6 x 1 + 6 x 2 36 x 1 4 x 1, x 2 0 Step 3: Determine the corners; Step 4: Evaluate the objective function and identify the optimal solution. Figure 6. 22 Optimal Solution Point Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 44

Chapter 6 - Linear Programming: Model Formulation and Graphical Solution 45