INTRODUCTION TO MANAGEMENT SCIENCE 13 e Anderson Sweeney

INTRODUCTION TO MANAGEMENT SCIENCE, 13 e Anderson Sweeney Williams Martin © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slides by JOHN LOUCKS St. Edward’s University Slide 1

Chapter 11 Waiting Line Models n n n Structure of a Waiting Line System Queuing Systems Queuing System Input Characteristics Queuing System Operating Characteristics Analytical Formulas Single-Channel Waiting Line Model with Poisson Arrivals and Exponential Service Times Multiple-Channel Waiting Line Model with Poisson Arrivals and Exponential Service Times Economic Analysis of Waiting Lines Single-Channel Waiting Line Model with Poisson Arrivals and Arbitrary Service Times Multiple-Channel Waiting Line Model with Poisson Arrivals, Arbitrary Service Times, and No Waiting Lines with Finite Calling Populations © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 2

Structure of a Waiting Line System n n Queuing theory is the study of waiting lines. Four characteristics of a queuing system are: • the manner in which customers arrive • the time required for service • the priority determining the order of service • the number and configuration of servers in the system. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 3

Structure of a Waiting Line System n n Distribution of Arrivals • Generally, the arrival of customers into the system is a random event. • Frequently the arrival pattern is modeled as a Poisson process. Distribution of Service Times • Service time is also usually a random variable. • A distribution commonly used to describe service time is the exponential distribution. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 4

Structure of a Waiting Line System n Queue Discipline • Most common queue discipline is first come, first served (FCFS). • An elevator is an example of last come, first served (LCFS) queue discipline. • Other disciplines assign priorities to the waiting units and then serve the unit with the highest priority first. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 5

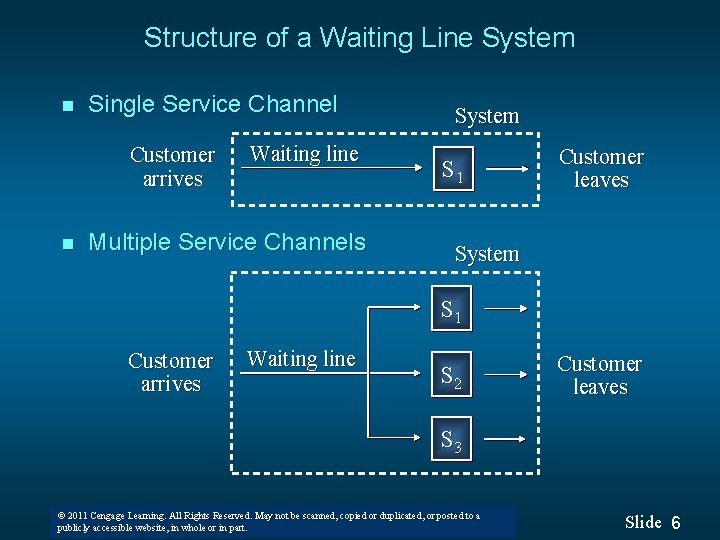
Structure of a Waiting Line System n Single Service Channel Customer arrives n Waiting line Multiple Service Channels System S 1 Customer leaves System S 1 Customer arrives Waiting line S 2 Customer leaves S 3 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 6

Queuing Systems n n A three part code of the form A/B/k is used to describe various queuing systems. A identifies the arrival distribution, B the service (departure) distribution and k the number of channels for the system. Symbols used for the arrival and service processes are: M - Markov distributions (Poisson/exponential), D Deterministic (constant) and G - General distribution (with a known mean and variance). For example, M/M/k refers to a system in which arrivals occur according to a Poisson distribution, service times follow an exponential distribution and there are k servers working at identical service rates. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 7

Queuing System Input Characteristics = the average arrival rate 1/ = the average time between arrivals µ = the average service rate for each server 1/µ = the average service time = the standard deviation of the service time © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 8

Queuing System Operating Characteristics P 0 Pn Pw Lq L Wq W = = = probability the service facility is idle probability of n units in the system probability an arriving unit must wait for service = average number of units in the queue awaiting service = average number of units in the system = average time a unit spends in the queue awaiting service = average time a unit spends in the system © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 9

Analytical Formulas n n For nearly all queuing systems, there is a relationship between the average time a unit spends in the system or queue and the average number of units in the system or queue. These relationships, known as Little's flow equations are: L = W and Lq = Wq © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 10

Analytical Formulas n n When the queue discipline is FCFS, analytical formulas have been derived for several different queuing models including the following: • M/M/1 • M / M/ k • M/G/1 • M/G/k with blocked customers cleared • M/M/1 with a finite calling population Analytical formulas are not available for all possible queuing systems. In this event, insights may be gained through a simulation of the system. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 11

M/M/1 Queuing System n n n Single channel Poisson arrival-rate distribution Exponential service-time distribution Unlimited maximum queue length Infinite calling population Examples: • Single-window theatre ticket sales booth • Single-scanner airport security station © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 12

Example: SJJT, Inc. (A) n M/M/1 Queuing System Joe Ferris is a stock trader on the floor of the New York Stock Exchange for the firm of Smith, Jones, Johnson, and Thomas, Inc. Stock transactions arrive at a mean rate of 20 per hour. Each order received by Joe requires an average of two minutes to process. Orders arrive at a mean rate of 20 per hour or one order every 3 minutes. Therefore, in a 15 minute interval the average number of orders arriving will be = 15/3 = 5. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 13

Example: SJJT, Inc. (A) n Arrival Rate Distribution Question What is the probability that no orders are received within a 15 -minute period? Answer P (x = 0) = (50 e -5)/0! = e -5 = . 0067 Question What is the probability that exactly 3 orders are received within a 15 -minute period? Answer P (x = 3) = (53 e -5)/3! = 125(. 0067)/6 = © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. . 1396 Slide 14

Example: SJJT, Inc. (A) n Arrival Rate Distribution Question What is the probability that more than 6 orders arrive within a 15 -minute period? Answer P (x > 6) = 1 - P (x = 0) - P (x = 1) - P (x = 2) - P (x = 3) - P (x = 4) - P (x = 5) - P (x = 6) = 1 -. 762 =. 238 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 15

Example: SJJT, Inc. (A) n Service Rate Distribution Question What is the mean service rate per hour? Answer Since Joe Ferris can process an order in an average time of 2 minutes (= 2/60 hr. ), then the mean service rate, µ, is µ = 1/(mean service time), or 60/2. = 30/hr. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 16

Example: SJJT, Inc. (A) n Service Time Distribution Question What percentage of the orders will take less than one minute to process? Answer Since the units are expressed in hours, P (T < 1 minute) = P (T < 1/60 hour). Using the exponential distribution, P (T < t ) = 1 - e-µt. Hence, P (T < 1/60) = 1 - e-30(1/60) = 1 -. 6065 =. 3935 = 39. 35% © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 17

Example: SJJT, Inc. (A) n Service Time Distribution Question What percentage of the orders will be processed in exactly 3 minutes? Answer Since the exponential distribution is a continuous distribution, the probability a service time exactly equals any specific value is 0. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 18

Example: SJJT, Inc. (A) n Service Time Distribution Question What percentage of the orders will require more than 3 minutes to process? Answer The percentage of orders requiring more than 3 minutes to process is: P (T > 3/60) = e-30(3/60) = e -1. 5 =. 2231 = 22. 31% © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 19

Example: SJJT, Inc. (A) n Average Time in the System Question What is the average time an order must wait from the time Joe receives the order until it is finished being processed (i. e. its turnaround time)? Answer This is an M/M/1 queue with = 20 per hour and = 30 per hour. The average time an order waits in the system is: W = 1/(µ - ) = 1/(30 - 20) = 1/10 hour or 6 minutes © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 20

Example: SJJT, Inc. (A) n Average Length of Queue Question What is the average number of orders Joe has waiting to be processed? Answer Average number of orders waiting in the queue is: Lq = 2/[µ(µ - )] = (20)2/[(30)(30 -20)] = 400/300 = 4/3 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 21

Example: SJJT, Inc. (A) n Utilization Factor Question What percentage of the time is Joe processing orders? Answer The percentage of time Joe is processing orders is equivalent to the utilization factor, /. Thus, the percentage of time he is processing orders is: / = 20/30 = 2/3 or 66. 67% © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 22

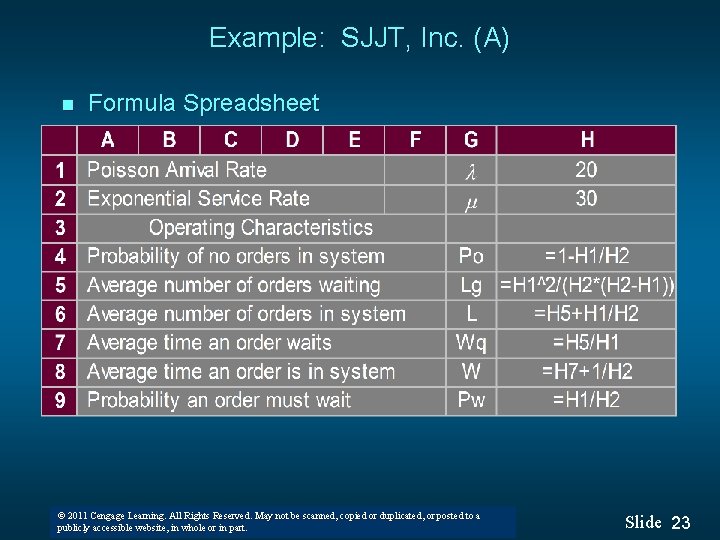
Example: SJJT, Inc. (A) n Formula Spreadsheet © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 23

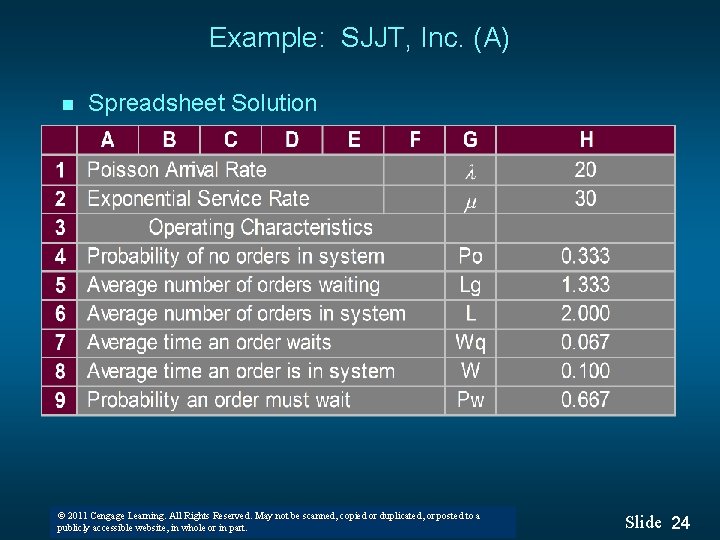
Example: SJJT, Inc. (A) n Spreadsheet Solution © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 24

M/M/k Queuing System n n n Multiple channels (with one central waiting line) Poisson arrival-rate distribution Exponential service-time distribution Unlimited maximum queue length Infinite calling population Examples: • Four-teller transaction counter in bank • Two-clerk returns counter in retail store © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 25

Example: SJJT, Inc. (B) n M/M/2 Queuing System Smith, Jones, Johnson, and Thomas, Inc. has begun a major advertising campaign which it believes will increase its business 50%. To handle the increased volume, the company has hired an additional floor trader, Fred Hanson, who works at the same speed as Joe Ferris. Note that the new arrival rate of orders, , is 50% higher than that of problem (A). Thus, = 1. 5(20) = 30 per hour. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 26

Example: SJJT, Inc. (B) n Sufficient Service Rate Question Why will Joe Ferris alone not be able to handle the increase in orders? Answer Since Joe Ferris processes orders at a mean rate of µ = 30 per hour, then = µ = 30 and the utilization factor is 1. This implies the queue of orders will grow infinitely large. Hence, Joe alone cannot handle this increase in demand. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 27

Example: SJJT, Inc. (B) n Probability of n Units in System Question What is the probability that neither Joe nor Fred will be working on an order at any point in time? Answer Given that = 30, µ = 30, k = 2 and ( /µ) = 1, the probability that neither Joe nor Fred will be working is: = 1/[(1 + (1/1!)(30/30)1] + [(1/2!)(1)2][2(30)/(2(30)-30)] = 1/(1 + 1) = 1/3 = . 333 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 28

Example: SJJT, Inc. (B) n Average Time in System Question What is the average turnaround time for an order with both Joe and Fred working? Answer The average turnaround time is the average waiting time in the system, W. L = Lq + ( /µ) = 1/3 + (30/30) = 4/3 W = L/ (4/3)/30 = 4/90 hr. = © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. 2. 67 min. Slide 29

Example: SJJT, Inc. (B) n Average Length of Queue Question What is the average number of orders waiting to be filled with both Joe and Fred working? Answer The average number of orders waiting to be filled is Lq. This was calculated earlier as 1/3. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 30

Example: SJJT, Inc. (B) n Formula Spreadsheet © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 31

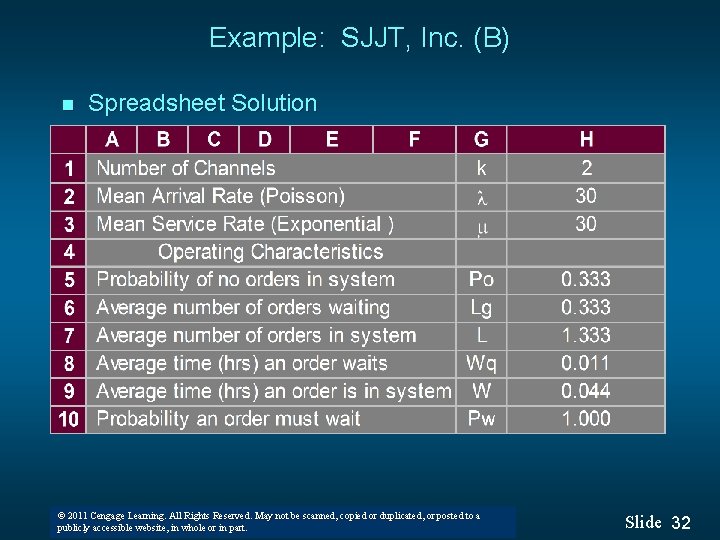
Example: SJJT, Inc. (B) n Spreadsheet Solution © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 32

Example: SJJT, Inc. (B) n Creating Special Excel Function to Compute P 0 Select the Tools pull-down menu Select the Macro option Choose the Visual Basic Editor When the Visual Basic Editor appears Select the Insert pull-down menu Choose the Module option When the Module sheet appears Enter Function Po (k, lamda, mu) Enter Visual Basic program (on next slide) Select the File pull-down menu Choose the Close and Return to MS Excel option © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 33

Example: SJJT, Inc. (B) n Visual Basic Module for P 0 Function Po(k, lamda, mu) Sum = 0 For n = 0 to k - 1 Sum = Sum + (lamda/mu) ^ n / Application. Fact(n) Next Po = 1/(Sum+(lamda/mu)^k/Application. Fact(k))* (k*mu/(k*mu-lamda))) End Function © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 34

Example: SJJT, Inc. (C) n Economic Analysis of Queuing Systems The advertising campaign of Smith, Jones, Johnson and Thomas, Inc. (see problems (A) and (B)) was so successful that business actually doubled. The mean rate of stock orders arriving at the exchange is now 40 per hour and the company must decide how many floor traders to employ. Each floor trader hired can process an order in an average time of 2 minutes. Based on a number of factors the brokerage firm has determined the average waiting cost per minute for an order to be $. 50. Floor traders hired will earn $20 per hour in wages and benefits. Using this information compare the total hourly cost of hiring 2 traders with that of hiring 3 traders. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 35

Example: SJJT, Inc. (C) n Economic Analysis of Waiting Lines Total Hourly Cost = (Total salary cost per hour) + (Total hourly cost for orders in the system) = ($20 per trader per hour) x (Number of traders) + ($30 waiting cost per hour) x (Average number of orders in the system) = 20 k + 30 L. Thus, L must be determined for k = 2 traders and for k = 3 traders with = 40/hr. and = 30/hr. (since the average service time is 2 minutes (1/30 hr. ). © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 36

Example: SJJT, Inc. (C) n Cost of Two Servers P 0 = 1 / [1+(1/1!)(40/30)]+[(1/2!)(40/30)2(60/(60 -40))] = 1 / [1 + (4/3) + (8/3)] = 1/5 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 37

Example: SJJT, Inc. (C) n Cost of Two Servers (continued) Thus, L = Lq + ( /µ) = 16/15 + 4/3 = 2. 40 Total Cost = (20)(2) + 30(2. 40) = hour © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. $112. 00 per Slide 38

Example: SJJT, Inc. (C) n Cost of Three Servers P 0 = 1/[[1+(1/1!)(40/30)+(1/2!)(40/30)2]+ [(1/3!)(40/30)3(90/(90 -40))] ] = 1 / [1 + 4/3 + 8/9 + 32/45] = 15/59 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 39

Example: SJJT, Inc. (C) n Cost of Three Servers (continued) Thus, L =. 1446 + 40/30 = 1. 4780 Total Cost = (20)(3) + 30(1. 4780) = $104. 35 per hour © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 40

Example: SJJT, Inc. (C) n System Cost Comparison 2 Traders 3 Traders Wage Cost/Hr $40. 00 60. 00 Waiting Cost/Hr $82. 00 44. 35 Total Cost/Hr $112. 00 104. 35 Thus, the cost of having 3 traders is less than that of 2 traders. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 41

M/D/1 Queuing System n n n Single channel Poisson arrival-rate distribution Constant service time Unlimited maximum queue length Infinite calling population Examples: • Single-booth automatic car wash • Coffee vending machine © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 42

Example: Ride ‘Em Cowboy! n M/D/1 Queuing System The mechanical pony ride machine at the entrance to a very popular J-Mart store provides 2 minutes of riding for $. 50. Children wanting to ride the pony arrive (accompanied of course) according to a Poisson distribution with a mean rate of 15 per hour. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 43

Example: Ride ‘Em Cowboy! n What fraction of the time is the pony idle? = 15 per hour = 60/2 = 30 per hour Utilization = / = 15/30 =. 5 Idle fraction = 1 – Utilization = 1 -. 5 = © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. . 5 Slide 44

Example: Ride ‘Em Cowboy! n What is the average number of children waiting to ride the pony? n What is the average time a child waits for a ride? (or 1 minute) © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 45

M/G/k Queuing System n n n Multiple channels Poisson arrival-rate distribution Arbitrary service times No waiting line Infinite calling population Example: • Telephone system with k lines. (When all k lines are being used, additional callers get a busy signal. ) © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 46

Example: Allen-Booth n M/G/k Queuing System Allen-Booth (A-B) is an OTC market maker. A broker wishing to trade a particular stock for a client will call on a firm like Allen-Booth to execute the order. If the market maker's phone line is busy, a broker will immediately try calling another market maker to transact the order. A-B estimates that on the average, a broker will try to call to execute a stock transaction every two minutes. The time required to complete the transaction averages 75 seconds. A-B has four traders staffing its phones. Assume calls arrive according to a Poisson distribution. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 47

Example: Allen-Booth This problem can be modeled as an M/G/k system with block customers cleared with: 1/ = 2 minutes = 2/60 hour = 60/2 = 30 per hour 1/µ = 75 sec. = 75/60 min. = 75/3600 hr. µ = 3600/75 = 48 per hour © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 48

Example: Allen-Booth n % of A-B’s Customers Lost Due to Busy Line First, we must solve for P 0 where k = 4 P 0 = 1 1 + (30/48)2/2! + (30/48)3/3! + (30/48)4/4! P 0 =. 536 continued © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 49

Example: Allen-Booth n % of A-B’s Customers Lost Due to Busy Line Now, Thus, with four traders 0. 3% of the potential customers are lost. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 50

Single-Channel Waiting Line Model with Poisson Arrivals and Arbitrary Service Times The Cutler University Student Union has one self service copying machine. On the average, 12 customers per hour arrive to make copies. (The arrival process follows a Poisson distribution. ) The time to copy documents follows approximately a normal distribution with a mean of 2. 5 minutes and a standard deviation of 30 seconds. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 51

Single-Channel Waiting Line Model with Poisson Arrivals and Arbitrary Service Times The Union manager has received several complaints from students regarding the long lines at the copier. Based of this information, determine: 1) the average number of customers waiting or using the copier. 2) the probability an arriving customer must wait in line. 3) the proportion of time the copier is idle. 4) the average time a customer must wait in line before using the copier. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 52

Single-Channel Waiting Line Model with Poisson Arrivals and Arbitrary Service Times This situation can be modeled as an M/G/1 system with: = 12 per hour = 12/60 =. 2/minute 1/µ = 2. 5 minutes µ = 1/(2. 5) =. 4 per minute s = 30 seconds =. 5 minutes © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 53

Single-Channel Waiting Line Model with Poisson Arrivals and Arbitrary Service Times n Average number of customers waiting or using the copier where Substituting the appropriate values gives: Thus L =. 26 + (. 2/. 4) =. 76 customers © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 54

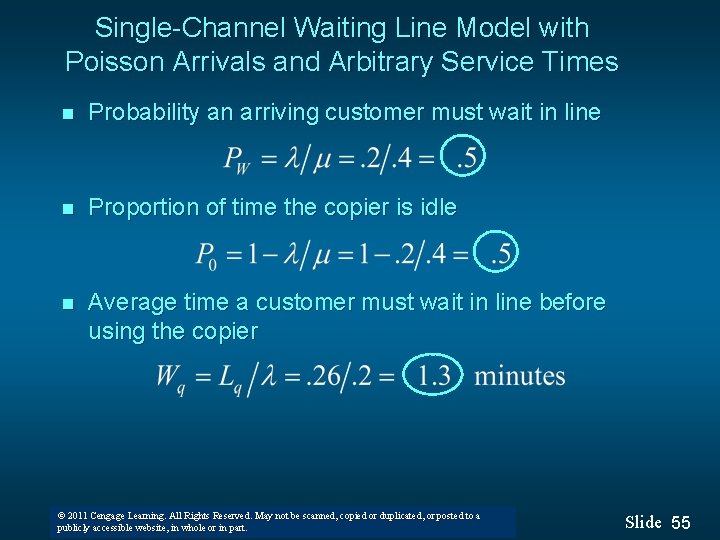
Single-Channel Waiting Line Model with Poisson Arrivals and Arbitrary Service Times n Probability an arriving customer must wait in line n Proportion of time the copier is idle n Average time a customer must wait in line before using the copier © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 55

Multiple-Channel Waiting Line Model with Poisson Arrivals, Arbitrary Service Times, and No Waiting Line Several firms are over-the-counter (OTC) market makers of Mega. Tech stock. A broker wishing to trade this stock for a client will call on these firms to execute the order. If the market maker's phone line is busy, a broker will immediately try calling another market maker to transact the order. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 56

Multiple-Channel Waiting Line Model with Poisson Arrivals, Arbitrary Service Times, and No Waiting Line Richardson and Company is one such OTC market maker. It estimates that on the average, a broker will try to call to execute a stock transaction every two minutes. The time required to complete the transaction averages 75 seconds. The firm has four traders staffing its phones. Assume calls arrive according to a Poisson distribution. What percentage of its potential business will be lost by Richardson? What percentage of its potential business would be lost if only three traders staffed its phones? © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 57

Multiple-Channel Waiting Line Model with Poisson Arrivals, Arbitrary Service Times, and No Waiting Line This problem can be modeled as an M/G/k system with block customers cleared with: 1/ = 2 minutes = 2/60 hour = 60/2 = 30 per hour 1/µ = 75 seconds = 75/60 minutes = 75/3600 hours µ = 3600/75 = 48 per hour © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 58

Multiple-Channel Waiting Line Model with Poisson Arrivals, Arbitrary Service Times, and No Waiting Line n Percentage of potential business that be lost when using 4 traders (k = 4) The system will be blocked when there are four customers in the system. Hence, the answer is P 4. continued © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 59

Multiple-Channel Waiting Line Model with Poisson Arrivals, Arbitrary Service Times, and No Waiting Line n Percentage of potential business that be lost when using 4 traders (k = 4) Now, Thus, with four traders 0. 3% of the potential customers are lost. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 60

Multiple-Channel Waiting Line Model with Poisson Arrivals, Arbitrary Service Times, and No Waiting Line n Percentage of potential business that be lost when using 3 traders (k = 3) The system will be blocked when there are three customers in the system. Hence, the answer is P 3. Thus, with three traders 2. 2% of the potential customers are lost. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 61

Waiting Lines with Finite Calling Populations Biff Smith is in charge of maintenance for four of the rides at the Rollerama Amusement Park. On the average, each ride operates four hours before needing repair. When repair is needed, the average repair time is 10 minutes. Assuming the time between machine repairs as well as the service times follow exponential distributions, determine: 1) the proportion of time Biff is idle, and 2) the average time a ride is "down" for repairs. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 62

Waiting Lines with Finite Calling Populations This problem can be modeled as an M/M/1 queue with a finite calling population of size N = 4 (rides). = 1/(4 hours) =. 25 per hour µ = 60/(10 minutes) = 6 per hour / =. 25/6 = 1/24 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 63

Waiting Lines with Finite Calling Populations n Proportion of time Biff is idle Hence, Biff is idle approximately 84% of the time. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 64

Waiting Lines with Finite Calling Populations n Average time a ride is "down" for repairs where Substituting the appropriate values gives: Lq = 4 - ((. 25+6)/. 25)(1 -. 840825) =. 020625 L =. 020625 + (1 -. 840825) =. 1798 Wq =. 020625/((4 -. 1798). 25) =. 021596 W =. 021596 + 1/6 =. 18826 hours or 11. 3 minutes © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 65

End of Chapter 11 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a © 2008 Thomson South-Western. All Rights Reserved publicly accessible website, in whole or in part. Slide 66