Introduction to logistic regression and Generalized Linear Models

Introduction to logistic regression and Generalized Linear Models Karen Bandeen-Roche, Ph. D Department of Biostatistics Johns Hopkins University July 14, 2011 Introduction to Statistical Measurement and Modeling

Data motivation v Osteoporosis data v Scientific question: Can we detect osteoporosis earlier and more safely? v Some related statistical questions: v How does the risk of osteoporosis vary as a function of measures commonly used to screen for osteoporosis? v Does age confound the relationship of screening measures with osteoporosis risk? v Do ultrasound and DPA measurements discriminate osteoporosis risk independently of each other?

Outline v Why we need to generalize linear models v Generalized Linear Model specification v Systematic, random model components v Maximum likelihood estimation v Logistic regression as a special case of GLM v Systematic model / interpretation v Inference v Example

v Regression for categorical outcomes Why not just apply linear regression to categorical Y’s? v Linear model (A 1) will often be unreasonable. v Assumption of equal variances (A 3) will nearly always be unreasonable. v Assumption of normality will never be reasonable

Introduction: Regression for binary outcomes v Yi = 1{event occurs for sampling unit i} = 1 if the event occurs = 0 otherwise. v pi = probability that the event occurs for sampling unit i : = Pr{Yi = 1} v Begin by generalizing random model (A 5): v Probability mass function: Bernoulli Pr{Yi = 1} = pi; Pr{Yi = 0} = 1 -pi all other yi occur with 0 probability

Binary regression v By assuming Bernoulli: (A 3) is definitely not reasonable v Var(Yi ) = pi(1 -pi) v Variance is not constant: rather a function of the mean v Systematic model v Goal remains to describe E[Yi|xi] v Expectation of Bernoulli Yi = pi v To achieve a reasonable linear model (A 1): describe some function of E[Yi|xi] as a linear function of covariates v g(E[Yi|xi]) = xi’β v Some common g: log, log{p/(1 -p)}, probit

General framework: Generalized Linear Models v Random model v Y~a density or mass function, f. Y, not necessarily normal v Technical aside: f. Y within the “exponential family” v Systematic model v g(E[Yi|xi]) = xi’β = ηi v “g” = “link function”; “xi’β” = “linear predictor” v Reference: Nelder JA, Wedderburn RWM, Generalized linear models, JRSSA 1972; 135: 370 -384.

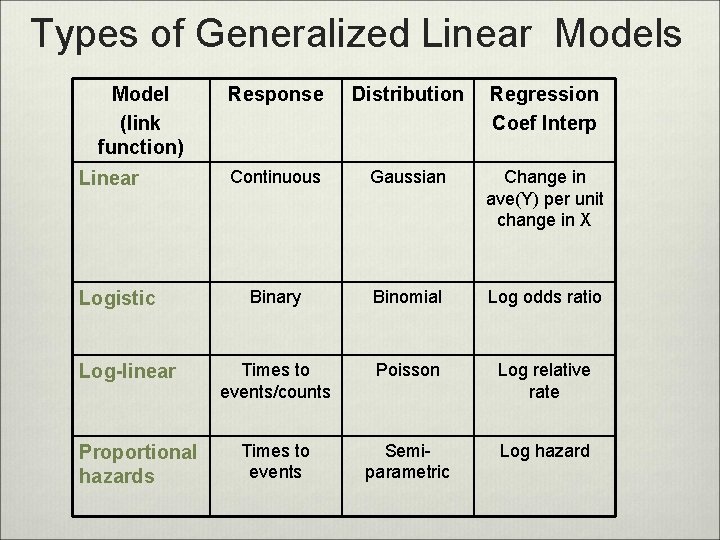
Types of Generalized Linear Models Model (link function) Linear Logistic Log-linear Proportional hazards Response Distribution Regression Coef Interp Continuous Gaussian Change in ave(Y) per unit change in X Binary Binomial Log odds ratio Times to events/counts Poisson Log relative rate Times to events Semiparametric Log hazard

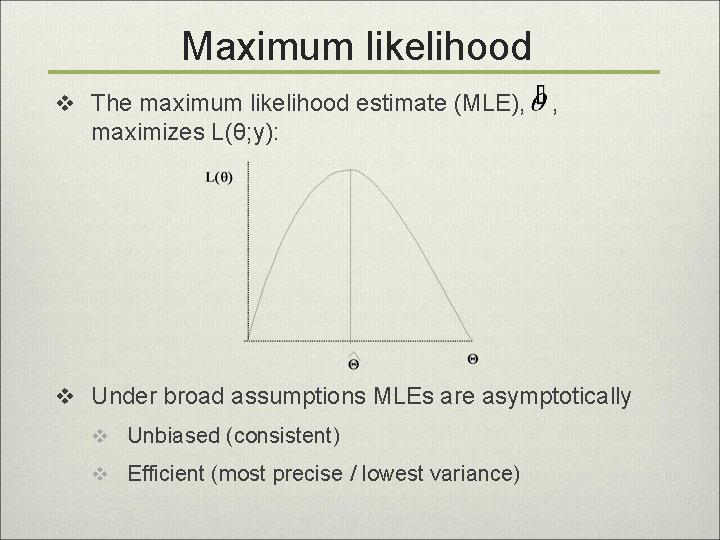
Estimation v Estimation: maximizes L(β, a; y, X) = v General method: Maximum likelihood (Fisher) v Given {Y 1, . . . , Yn} distributed with joint density or mass function f. Y(y; θ), a likelihood function L(θ; y) is any function (of θ) that is proportional to f. Y(y; θ). v If sampling is random, {Y 1, . . . , Yn} are statistically independent, and L(θ; y) α product of individual f.

Maximum likelihood v The maximum likelihood estimate (MLE), , maximizes L(θ; y): v Under broad assumptions MLEs are asymptotically v Unbiased (consistent) v Efficient (most precise / lowest variance)

Logistic regression v Yi binary with pi = Pr{Yi = 1} v Example: Yi = 1{person i diagnosed with heart disease} v Simple logistic regression (1 covariate) v Random Model: Bernoulli / Binomial v Systematic Model: log{pi/(1 - pi)}= β 0 + β 1 xi v log odds; logit(pi) v Parameter interpretation v β 0 = log(heart disease odds) in subpopulation with x=0 v β 1 = log{px+1/(1 -px+1)}- log{px/(1 -px)}

Logistic regression Interpretation notes v β 1 = log{px+1/(1 -px+1)}- log{px/(1 -px)} = v exp(β 1) = = odds ratio for association of prevalent heart disease with each (say) one year increment in age = factor by which odds of heart disease increases / decreases with each 1 -year cohort of age

Multiple logistic regression v Systematic Model: log{pi/(1 - pi)}= β 0 + β 1 xi 1 + … + βpxip v Parameter interpretation v β 0 = log(heart disease odds) in subpopulation with all x=0 v βj = difference in log outcome odds comparing subpopulations who differ by 1 on xj, and whose values on all other covariates are the same v “Adjusting for, ” “Controlling for” the other covariates v One can define variables contrasting outcome odds differences between groups, nonlinear relationships, interactions, etc. , just as in linear regression

Logistic regression - prediction v Translation from ηi to pi v log{pi/(1 - pi)}= β 0 + β 1 xi 1 + … + βpxip v Then = logistic function of ηi v Graph of pi versus ηi has a sigmoid shape

GLMs - Inference v The negative inverse Hessian matrix of the log likelihood function characterizes Var( ) (adjunct) v SE( ) obtained as square root of the jth diagonal entry v Typically, substituting for β v “Wald” inference applies the paradigm from Lecture 2 v Z= β 0 j is asympotically ~ N(0, 1) under H 0: βj= v Z provides a test statistic for H 0: βj= β 0 j versus HA: βj≠ β 0 j v ± z(1 -α/2) SE{ } =(L, U) is a (1 -α)x 100% CI for βj v {exp(L), exp(U)} is a (1 -α)x 100% CI for exp(βj)

GLMs: “Global” Inference v Analog: F-testing in linear regression v The only difference: log likelihoods replace SS v Hypothesis to be tested is H 0: βj 1=. . . =βjk = 0 v Fit model excluding xj 1, . . . , xjpj: Save -2 log likelihood = Ls v Fit “full” (or larger) model adding xj 1, . . . , xjpj to smaller model. Save -2 log likelihood = LL v Test statistic S = Ls - LL v Distribution under null hypothesis: χ2 pj v Define rejection region based on this distribution v Compute S v Reject or not as S is in rejection region or not

GLMs: “Global” Inference v Many programs refer to “deviance” rather than -2 log likelihood v This quantity equals the difference in -2 log likelihoods between ones fitted model and a “saturated model” v Deviance measures “fit” v Differences in deviances can be substituted for differences in -2 log likelihood in the method given on the previous page v Likelihood ratio tests have appealing optimality properties

Outline: A few more topics v Model checking: Residuals, influence points v ML can be written as an iteratively reweighted least squares algorithm v Predictive accuracy v Framework generalizes easily

Main Points v Generalized linear modeling provides a flexible regression framework for a variety of response types v Continuous, categorical measurement scales v Probability distributions tailored to the outcome v Systematic model to accommodate v Measurement range, interpretation v Logistic regression v Binary responses (yes, no) v Bernoulli / binomial distribution v Regression coefficients as log odds ratios for association between predictors and outcomes

Main Points v Generalized linear modeling accommodates description, inference, adjustment with the same flexibility as linear modeling v Inference v “Wald”- statistical tests and confidence intervals via parameter estimator standardization v “Likelihood ratio” / “global” – via comparison of log likelihoods from nested models