Introduction to Logic Thinkingthe logical way Logic l

Introduction to Logic Thinking…the logical way

Logic l l l Logic is the art/science of good reasoning Logic is the study of arguments Over the next three weeks we will investigate the following concepts: • • Propositions Conditional Statements Validity Biconditional Statements/Definitions And/Or Statements Axioms (Postulates) and Undefined Terms Negations and Contrapositives Indirect Arguments

Aristotle l l l Born 384 BCE Tutored Alexander the Great Wrote formal rules of logic

Propositions At the most primitive level logic deals with propositions A proposition is: A declarative statement not a question or a command Either true or false not ambiguous

Example of propositions include: l It is raining. l You are in math class. l Water is wet. l Mr. Thomson has six toes on his left foot. l You are carrying an umbrella. l An uranium atom is 92 protons. l 5+2=9

The following are not propositions. Can you explain why? l Is it raining? -This a question. It is not declarative. l Shut the door. l -This a command. It is not declarative. La la la la -This a string of meaningless words. It is not declarative l x+5=8 -This is an ambiguous statement. We don’t know what x is. If x equals 3 then it is true, but if x is equal to something else…

One question… In a country there are two cities. One of the cities is populated by people that always tell the truth. The other city is filled with people that never tell the truth. While attempting to make it to the city of the truth tellers you come to a fork in the road. One path leads to the truth tellers, the other to the liars. There is a resident of one of the two cities (you don’t know which) sitting along side the road. What one question do you ask him, in order to know the path to your destination?

Is the following a proposition? What is the validity of the proposition? (validity: true or false) l Lansing is the capitol of Michigan. • This is a proposition and it is true.

Is the following a proposition? What is the validity of the proposition? l There are no fish in Stoney Creek. • This is a proposition and it is false.

Is the following a proposition? What is the validity of the proposition? l Tennis is a sport. • This is a proposition and it is true.

Is the following a proposition? What is the validity of the proposition? l Is cross country a sport? • This is not a proposition—it is a question.

Is the following a proposition? What is the validity of the proposition? l Run cross country. • This is not a proposition—it is a command.

Is the following a proposition? What is the validity of the proposition? l 2 (5 + 3)/2 = 8 • This is a proposition and it is true.

Is the following a proposition? What is the validity of the proposition? l 2 x=8 • This is not a proposition—it is ambiguous.

Is the following a proposition? What is the validity of the proposition? l y=mx+b • This is not a proposition—it is ambiguous.

Is the following a proposition? What is the validity of the proposition? l I am Kermit T. Frog. • This is a proposition and it is false.

Conditionals

A conditional is any statement in the following form: If P, then Q. If you are good, then you will get a piece of sausage.

There are two parts to a conditional • Antecedent: This is the proposition that happens first • Consequent: This is the proposition that happens second

In the example: If you get a C on your exam, then you will pass the course. There are two propositions: P: You get a C on your exam Q: You pass the course

There are many ways to write a conditional l l l If p, then q. p implies q. q follows from p. p is sufficient for q. q is necessary for p. q if p. p q

Identify the antecedent and consequent in each of the following conditionals: l If you give a man a fish, then he will eat for a day. l If you teach a man to fish, he will eat for a lifetime. l If I am tired, then I will go to bed. l I will wear my rain coat, if it is raining.

Validity l l l Validity is the truth value of a statement Propositions are either true or false Conditionals are either true or false

Validity of a Conditional l A conditional is like a contract: if the first part happens then the second part has to happen as well.

I will pay you $5, if you cut my grass. l l l Antecedent: You cut my grass. Consequent: I pay you $5. Symbolically • P: You cut my grass • Q: I pay you $5 • P Q

There are 4 ways this could turn out 1. 2. 3. 4. You cut my grass, and I pay you $5. You cut my grass, and I don’t pay you $5. You don’t cut my grass, and I don’t pay you $5. Only option 2 is the result of an invalid contract. Option 2 is a counterexample to the conditional.

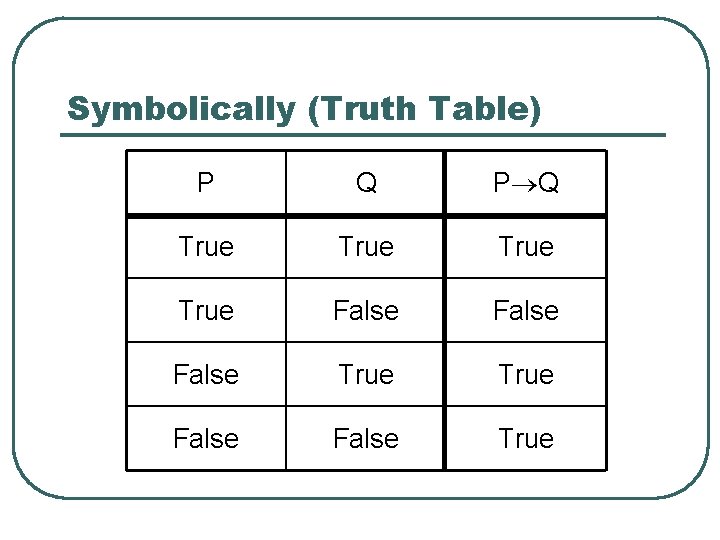
Symbolically (Truth Table) P Q True False True False True

Truth Table l A truth table displays the relationships between the truth values of propositions, and combinations of propositions.

Notice the conditional is true if the antecedent is false. A false statement implies anything. P Q True False True False True

Counter-example l l A conditional is false only when there exists, or could exist, a counter-example to it. In a counter-example the antecedent is true, but the consequent is false.

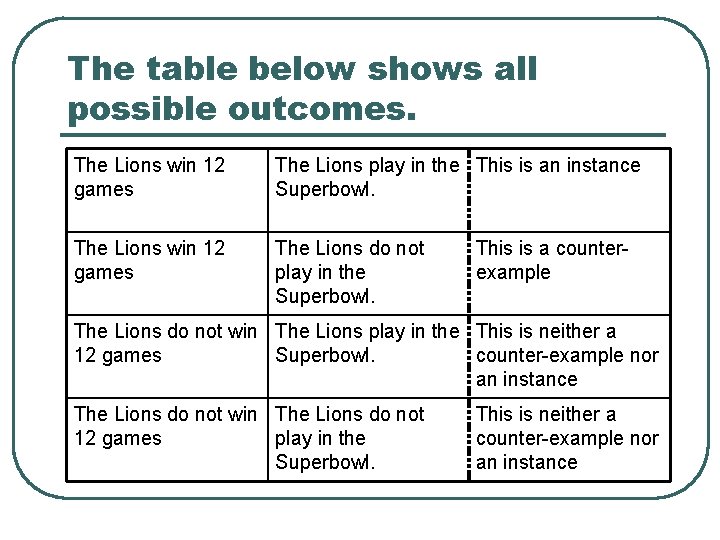
If the Lions win 12 games, then they will play in the Superbowl. Antecedent: The Lions win 12 games. l Consequent: The Lions play in the Superbowl. State an instance of the conditional. l The Lions win 12 games and play in the Superbowl. State a counter-example of the conditional. The Lions win 12 games and do not play in the Superbowl.

The table below shows all possible outcomes. The Lions win 12 games The Lions play in the This is an instance Superbowl. The Lions win 12 games The Lions do not play in the Superbowl. This is a counterexample The Lions do not win The Lions play in the This is neither a 12 games Superbowl. counter-example nor an instance The Lions do not win The Lions do not 12 games play in the Superbowl. This is neither a counter-example nor an instance

It only takes one counter-example to show that a conditional is false l There are two ways to prove conditional is true: • Show that it is true for every possible instance • of the antecedent Show that the counter-example does not exist.

Consider the following conditionals, and provide a counterexample to each. l l l If a figure is a polygon then it is a triangle. If you go to Stoney Creek H. S. , then you have Mr. Thomson for math. If you are 16, then you have a license to drive.

If a figure is a polygon then it is a triangle. l A square is a polygon that is not a triangle.

If you go to Stoney Creek H. S. , then you have Mr. Thomson for math. l Kelsey goes to Stoney Creek H. S. , but does not have Mr. Thomson for math.

If you are 16, then you have a license to drive. l Lauren is 16, and does not have a drivers license.

You have 9 balls, equally big, equally heavy - except for one, which is a little heavier. How would you identify the heavier ball if you could use a pair of balance scales only twice?

And, Or Propositions can be linked together using conjunction (and), or a disjunction (or).

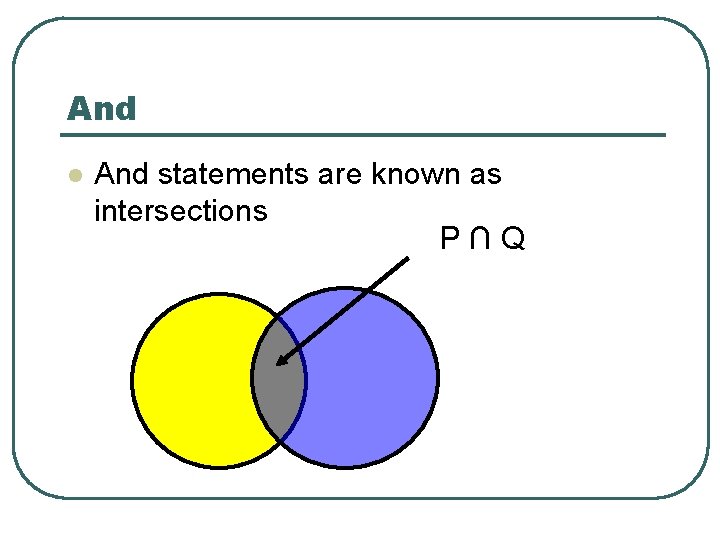
Conjunctions l Conjunctions are “And” statements l The ∩ symbol indicates “And” l P ∩ Q is read “P and Q”

And l And statements are known as intersections P∩Q

A conjunction is true iff both components are true. P Q P∩Q True False True False

Given the following propositions state the validity of the conjunctions. l l P: 4 is an even number Q: 7 is an even number R: 8 is an odd number S: 5 is an odd number l l P∩Q • False P∩R • False R∩S • False S∩Q • False

Identify all propositions l If you need to buy milk and eggs, then you will shop at Kroger. • P: You need to buy milk. • Q: You need to buy eggs. • R: You will shop at Kroger. • P∩Q→R

Identify all propositions l If a figure is a square, then it is equilateral and equiangular. • P: A figure is a square. • Q: A figure is equilateral. • R: A figures is equiangular. • P→Q∩R

Identify all propositions l In order to be a president of the U. S. it is necessary to be over the age of 35, and a natural born citizen. • • • If a person is the president of the U. S. , then they are over the age of 35, and a natural born citizen. P: A person is the president of the U. S. Q: A person is over the age of 35. R: A person is a natural born citizen. P→Q∩R

Identify all propositions l I will wear my boots and carry an umbrella, if it is raining. • P: It is raining. • Q: I will wear my boots. • R: I will carry an umbrella. • P→Q∩R

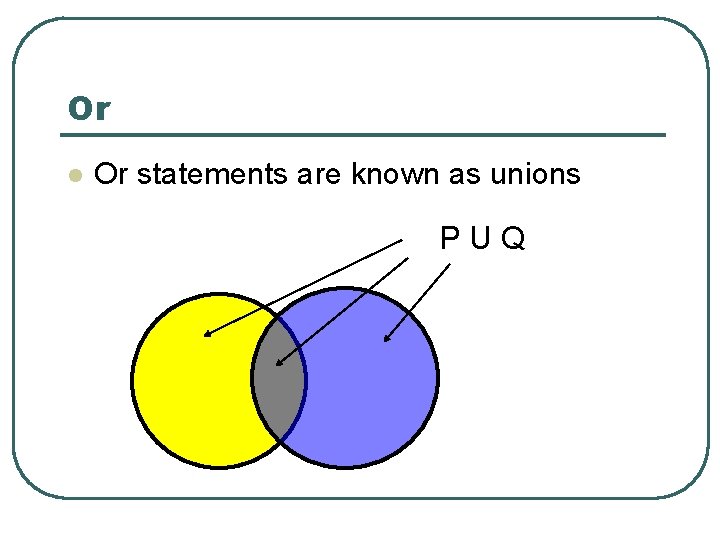
Disjunctions l Disjunctions are “Or” statements l The U symbol indicates “Or” l P U Q is read “P or Q”

Or l Or statements are known as unions PUQ

A disjunction is true if at least one of the components is true. P Q PUQ True True False False

Given the following propositions state the validity of the disjunctions. l l P: 4 is an even number Q: 7 is an even number R: 8 is an odd number S: 5 is an odd number l l PUQ • True PUR • True RUQ • False SUQ • True

Identify all propositions l If you run to school every day, you will be in great shape or sweaty. • P: You run to school every day. • Q: You will be in great shape. • R: You will be sweaty. • P→ Q U R

Identify all propositions l You can fly or drive if you want to go travel to Florida. • P: You want to travel to Florida. • Q: You can fly. • R: You can drive. • P→ Q U R

Negations l l l An important part of logic is the negation of a proposition If the proposition is “p”, then the negation is “not p”. Symbolically negations are indicated with the “~” or “¬”

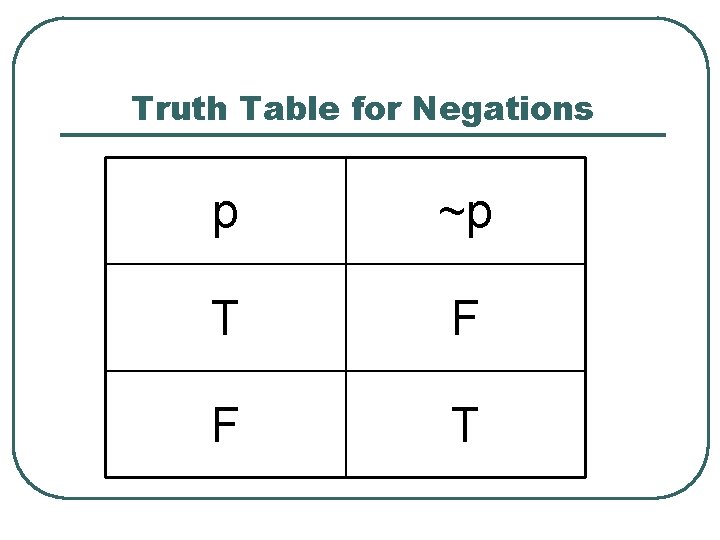
Truth Table for Negations p ~p T F F T

Negating propostions l It is raining. l It is Monday. l 5 + 4 = 9. l A figure is a triangle. • It is not raining. • It is not Monday. • 5 + 4 ≠ 9. • A figure is not a triangle.

Negating “And” statements l l l Recall that an “And” statement is only true when both propositions are true. The negation of “P ∩ Q” is “~P U ~Q” Notice the change from “and” to “or”.

An Example of Negating “And” Statements. l l Negate the statement: “It is raining and it is Monday. ” It is not raining, or it is not Monday

Negating Or Statements l l l Recall that an “Or” statement is true when either proposition is true. The negation of “P U Q” is “~P ∩ ~Q”. Notice the change from “or” to “and”.

An Example of Negating “or” Statements. l l Negate the statement: “Mr. Thomson drives a purple truck, or pianos are heavy. ” Mr. Thomson does not drive a purple truck, and pianos are not heavy.

A slug crawls up a well 75 inches deep, starting from the bottom. Each day it crawls up 5 inches, and each night it slides down 4 inches. When will it reach the top of the well?

Converse l If you replace the antecedent proposition with the consequent proposition you create a converse.

Example of a converse P: You cut my grass Q: I pay you $5 • P Q is the conditional. • If you cut my grass, then I will pay you $5. • The converse is Q P. • If I pay you $5, then you will cut my grass.

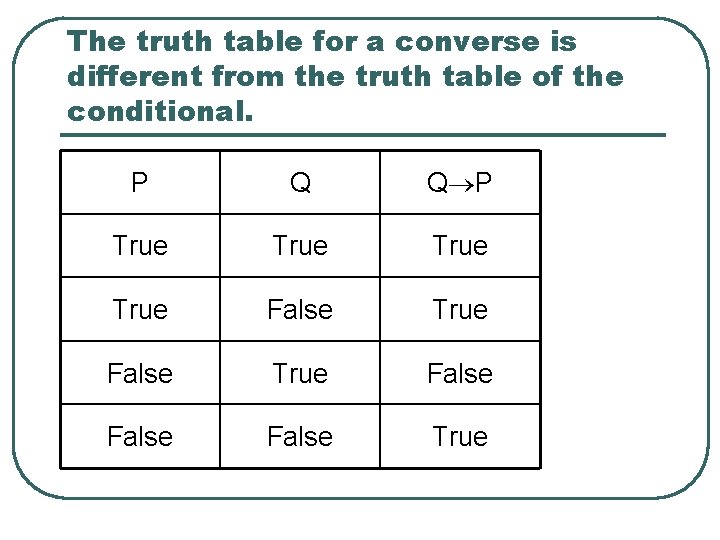
The truth table for a converse is different from the truth table of the conditional. P Q Q P True False True False True

The validity of a conditional and the validity of its converse are not related. l If a shape is a polygon, then it is a triangle. • This is false. • Counter-example: it is not a triangle. l A square is a polygon, but If a shape is a triangle then it is a polygon. • This is true. The definition of triangle says that a triangle must be a polygon.

In the following conditionals: l l l State the antecedent. State the consequent. If you can, state the validity of the conditional. State the converse of the conditional. If you can, state the validity of the converse.

All frogs are amphibians. l l l Antecedent: Something is a frog. Consequent: Something is an amphibian. Validity: True; by definition a frog must be an amphibian Converse: All amphibians are frogs. Validity: False; a salamander is an amphibian, but is not a frog.

You will get a ticket, if you are speeding. l l l Antecedent: You are speeding. Consequent: You get a ticket. Validity: False; I have sped and not gotten a ticket. Converse: If you get a ticket, then you were speeding. Validity: False; I got a ticket for parking, but I was not speeding.

Biconditional l If a conditional is true, and it’s converse is also true, then the statement is a biconditional.

If a polygon has three sides then it is a triangle. l l l Antecedent: A polygon has three sides. Consequent: It is a triangle. Validity: True Converse: If a polygon is a triangle, then it has three sides. Validity: True

Definition of a triangle: A polygon is a triangle if and only iff it has three sides. l All good definitions are biconditional statements.

Biconditionals are statements of the form P if and only if Q. l l l This can be shortened to P iff Q Or symbolically P↔Q A polygon is a triangle iff it has three sides.

Give a biconditional (iff) definition of the following terms: l Hexagon: l Square: l Mammal: l Beautiful: l Terrorist:

Connect each utility with each house. Utility lines may not intersect, run through another utility, nor may they run through a house. You may rearrange the utilities or houses, however you would like.

All good definitions have three characteristics: l l l include only words that are commonly understood, defined earlier, or purposely left undefined. can be expressed as a biconditional include only necessary information

What is wrong with these definitions? l A polygon is a triangle iff it has three sides and the sum of the angles is 180º • Extra information l A frog is an amphibian. l A widget is a thingamabob iff it has at least ½ of a doohickey. • Not a biconditional • Undefined terms.

Undefined Terms l l Terms (words) are defined with other terms (words) Eventually you will use a term to define it self This is circular reasoning (using the argument to support the argument) A logical systems must begin with a set of undefined terms.

Undefined Terms in Euclidean Geometry l l Point Line Plane We will use these terms to define all other terms in geometry

Miss English, Mrs. French, and Ms. Lapp all went on vacation recently, one to England, one to France, and one to Lapland. If only one of the following four statements is true, who went where? l l Ms. Lapp went to England Ms. Lapp did not go to France Miss English did not go to Lapland

Review for Quiz 2 l A proposition is a declarative sentence which is either true or false, but not both. • It is raining. • A bat is a mammal • 6 + 8 = 14 l The above examples are instances of simple statements, because they do not contain basic connections.

Basic Connectors l l l And • It is raining and I am wearing boots Or • It is raining or I am wearing boots If. . . then. . . • If it is raining, then I am wearing boots if and only if • It is raining if and only if I am wearing boots not • It is not raining

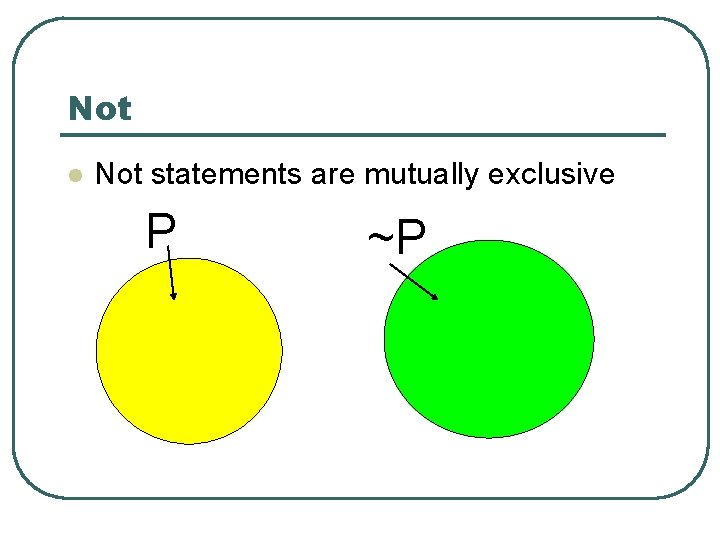
Not l Not statements are mutually exclusive P ~P

Propositions and their negations l P: It is raining. l ~P: It is not raining. l Q: 28 is even. l ~Q: 28 is odd. l R: Today is a weekday. l ~R: Today is a weekend. l S: It is sunny l ~S: It is not sunny

Conjunctions, Disjunctions & Negations

A conditional is any statement in the following form: If P, then Q. l l Conditionals are only true if a counterexample cannot exist. A counter-example is a case where the antecedent is true but the consequent is not.

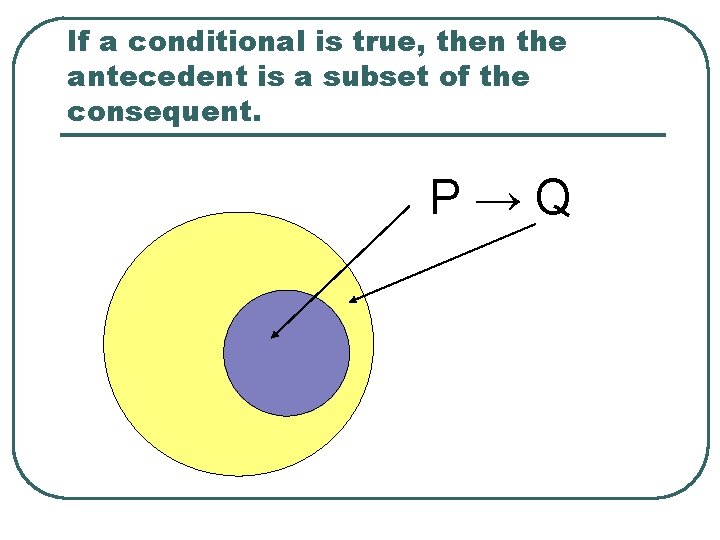
If a conditional is true, then the antecedent is a subset of the consequent. P→Q

An inverse of a conditional is the negation of the antecedent and the consequent. l l l ~P→~Q is the inverse of P→Q. Consider the conditional: If it is sunny, then I will go to the beach. The inverse is: If it is not sunny, then I will not go to the beach

Converse, Inverse l Converse of P → Q is Q → P • The validity of a conditional does not affect the validity of its converse. • If a figure is a triangle then it is a polygon. • True • If a figure is a polygon then it is a triangle l • False Inverse of P → Q is ~P → ~Q • The validity of a conditional does not affect the validity of its inverse • If a figure is not a triangle then it is not a polygon.

Indirect reasoning l l l We will study two methods of indirect reasoning. Ruling out possibilities Contrapositive

The game of Clue is based on ruling out possibilities. l l A direct method of knowing is to look into the “Confidential” envelope. The indirect method is to rule out all of the possibilities that are not in the envelope.

Ruling out possibilities is useful if: l l You have a finite set of possibilities You have a method for eliminating those possibilities.

Troubleshooting l Troubleshooting is a form of problem solving. It is the systematic search for the source of a problem so that it can be solved. Troubleshooting is used in many fields such as system administration and electronics. Normally a process of elimination is used to isolate possible causes of problems.

My car won’t start. l What kind a questions do you ask in order to diagnose the problem? • Are you turning the key? • Is there gas in the tank? • Does the engine turn over? • Do the lights work? • Are there any sounds when you turn the key?

What else could you troubleshoot?

A contrapositive of a conditional is the inverse of the converse. l l Conditional: P→Q Contrapositive: ~Q→~P If you get a C on your exam, then you will pass the course. If you don’t pass the course, then you didn’t get a C on the exam.

Validity of the contrapositive l The contrapositive has the same validity as the conditional.

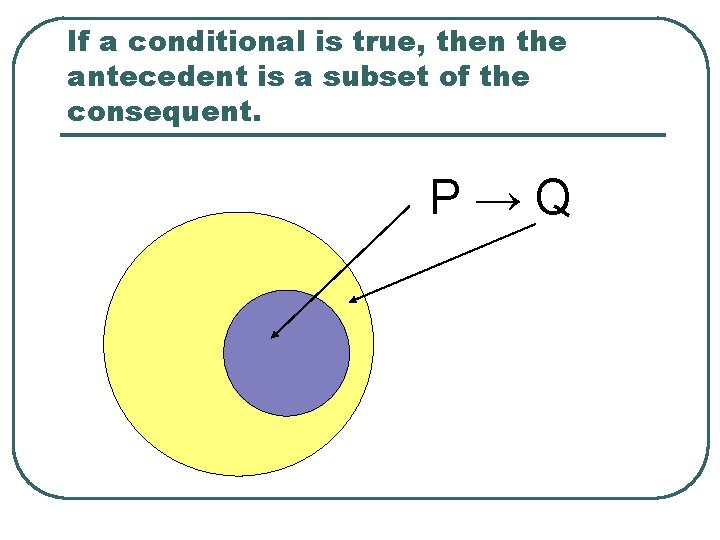
If a conditional is true, then the antecedent is a subset of the consequent. P→Q

All German Shepherds are dogs. Rewritten as an if then: -If it is a German Shepherd, then it is a dog Converse: -If it is a dog, then it is a German Shepherd Contrapositive: -If it is not a dog, then it is not a German Shepherd.

I will wear my boots, if it looks like snow. l If I wear my boots, it looks like snow. l If it does not look like snow, then I will not wear my boots. • Converse • Inverse l If I don’t wear my boots, it doesn’t look like snow. • Contrapositive

All math teachers are men. Rewritten as an if then: -If it is a math teacher, then it is a man. Converse: -If it is a man, then it is a math teacher. Contrapositive: -If it is not a man, then it is not a math teacher.

All math teachers are men. l l Antecedent: • A person is a math teacher. • The person is a man. • These are all instances of the conditional • • These are all counter-examples of the conditional The conditional is false Consequent Mr. Thomson, Mr. Kramer, Mr. Treat, Mr. Lougheed Mrs. Loveland, Mrs. Rodger, Mrs. Taylor, Mrs. Gumz, Mrs. Kaschalk, Mrs. Balinski