Introduction to Logic Propositional Resolution Michael Genesereth Computer

Introduction to Logic Propositional Resolution Michael Genesereth Computer Science Department Stanford University

Infinitely Many Choices Or Introduction 1. p Premise 2. q Premise 3. p | ? ? ? Or Introduction Assumption: 1. p ⇒ q 2. q ⇒ r 3. | ? ? ? Premise Assumption

Propositional Resolution The Resolution Principle is a rule of inference. Using the Resolution Principle alone (without axiom schemata or other rules of inference), it is possible to build a proof system (called Resolution) that is can prove everything that can be proved in Fitch. The search space using the Resolution Principle is much smaller than that of natural deduction systems.

Programme Clausal Form Resolution Rule of Inference Resolution Method

Clausal Form

Clausal Form Propositional resolution works only on expressions in clausal form. Fortunately, it is possible to convert any set of Propositional Logic sentences into a logically equivalent set of sentences in clausal form.

Clausal Form A literal is either an atomic sentence or a negation of an atomic sentence. p, Øp A clausal sentence is either a literal or a disjunction of literals. p, Øp, p Ú Øq A clause is a set of literals. {p}, {Øp}, {p, Øq}

Empty Sets The empty clause {} is unsatisfiable. Why? It is equivalent to an empty disjunction.

Conversion. Inseado to Clausal Form Implications Out:

Conversion to Clausal Form Implications Out: Negations In:

Conversion Inseado to Clausal Form Distribution

Conversion Inseado to Clausal Form Distribution Operators Out

Equivalence Good News: The result of converting a set of sentences is logically equivalent to that set of sentences. Upshot: Whatever we prove from clausal form is logically entailed by the original sentences.

Resolution Principle

Intuition Propositional Resolution Premises: {p, q} and {¬q, r} If q is false, then the first clause tells us p must be true. If q is true, then the second clause tells us r must be true. Conclusion: {p, r}

Resolution Principle Propositional Resolution {φ1, … , χ, … , φm} {ψ1, … , Øχ, … , ψn} {φ1, … , φm, ψ1, … , ψn}

Example Propositional Resolution {p, q} {Øq, r} {p, r}

Example Propositional Resolution {p, q} {Øp, q} {q}

Example Propositional Resolution {p, q, r} {Øp} {q, r}

Example Propositional Resolution {p} {Øp} {}

Example Propositional Resolution {p, q} {Øp, Øq} {q, Øq} {p, Øp}

Example Propositional Resolution {p, q} {Øp, Øq} {} Wrong!!!

Example Propositional Resolution p⇒ q p {Øp, q} {p} q {q}

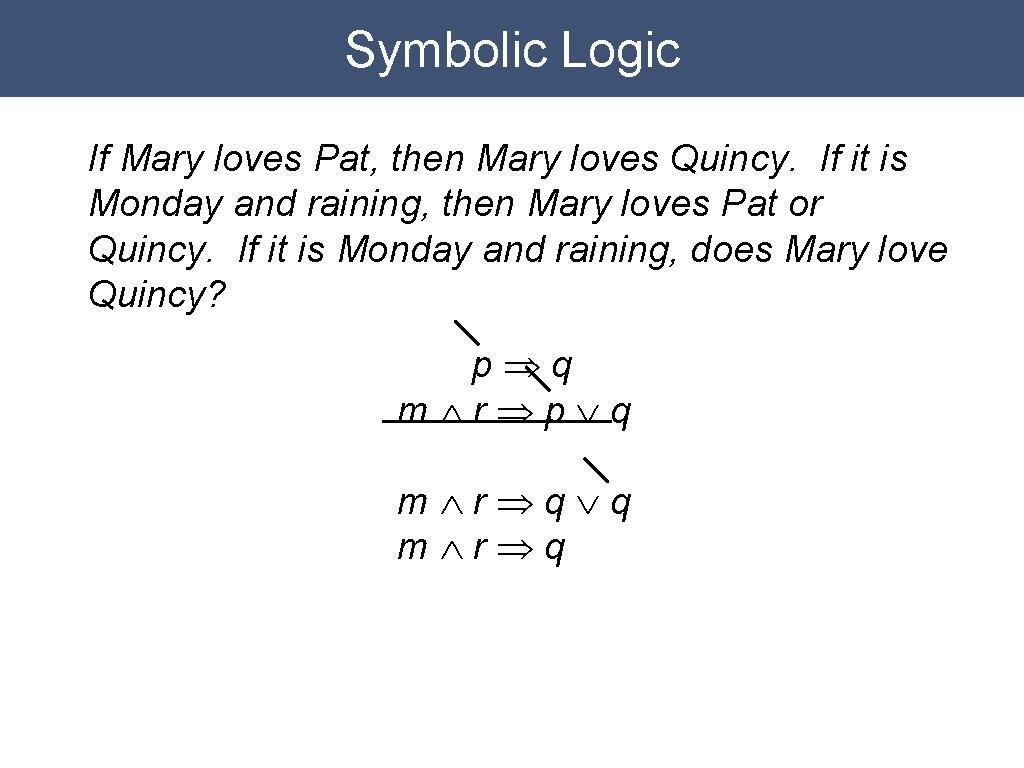
Symbolic Logic If Mary loves Pat, then Mary loves Quincy. If it is Monday and raining, then Mary loves Pat or Quincy. If it is Monday and raining, does Mary love Quincy? pÞq mÙrÞpÚq mÙrÞq

Example Propositional Resolution p⇒q m Ù r ⇒ pÚ q {Øp, q} {Øm, Ør, p, q} mÙr⇒ q {Øm, Ør, q}

Resolution Reasoning

Resolution Derivation A resolution derivation of a conclusion from a set of premises is a finite sequence of clauses terminating in the conclusion in which each clause is either a premise or the result of applying the resolution principle to earlier elements of the sequence.

Example 1. {Øp, r} Premise 2. {Øq, r} Premise 3. {p, q} Premise 4. {q, r} 1, 3 5. {r} 2, 4

Resolution Complete Resolution Not Generatively Complete Bad News: Using the Resolution Principle alone, it is not possible to generate every clause that is logically entailed by a set of premises. Premises: {p} and {q} Conclusion: {p, q} Premises: {} Conclusion: {p, Øp} But resolution cannot generate these results!

Resolution Unsatisfiability Resolution Determines Not Generatively Complete Good News: If a set of clauses is unsatisfiable, it is possible to derive the empty clause using the Resolution Principle. 1. 2. 3. 4. 5. 6 7 {p, q} {p, Øq} {Øp, Øq} {p} {Øp} {} Premise 1, 2 3, 4 5, 6

Resolution Method Unsatisfiability Determination: If a set of clauses is unsatisfiable, it is possible to derive the empty clause using the Resolution Principle. Unsatisfiability Theorem: D ⊨ j if and only if D È {Øj} is unsatisfiable. Resolution Method: To prove that a set Δ of sentences logically entails a conclusion φ, write Δ ∪ {¬φ} in clausal form and derive the empty clause. 34

Proof 1. 2. 3. 4. 5. {p} {q} {Øq, r} {Ør} 6. 7. 8. {q} {r} {} Premise Negated Goal 1, 2 6, 4 7, 5 36

Proof 1. {p} 2. {q} 3. {Øp} 4. {} Premis e 1, 3 38

Soundness and Completeness

Logical Entailment and Provability Completeness A set of premises D logically entails a conclusion j (D |= j) if and only if every interpretation that satisfies D also satisfies j. If there exists a proof of a sentence φ from a set Δ of premises using the rules of inference in R, we say that φ is provable from Δ using R (written Δ ⊢R φ).

Soundness and Completeness A proof system is sound if and only if every provable conclusion is logically entailed. If Δ ⊢ φ, then Δ ⊨ φ. A proof system is complete if and only if every logical conclusion is provable. If Δ ⊨ φ, then Δ ⊢ φ.

Resolution Theorem: Resolution is sound and complete for Propositional Logic. D |= j if and only if Δ ⊢Resolutin φ. Upshot: The truth table method and the proof method succeed in exactly the same cases!

Practical Matters

Strategies Elimination Strategies (Constraints on clauses): Identical Clause Elimination Pure Literal Elimination Tautology Elimination Subsumption Elimination Restriction Strategies (Constraints on inferences): Unit Restriction Input Restriction Linear Restriction Set of Support Restriction 44

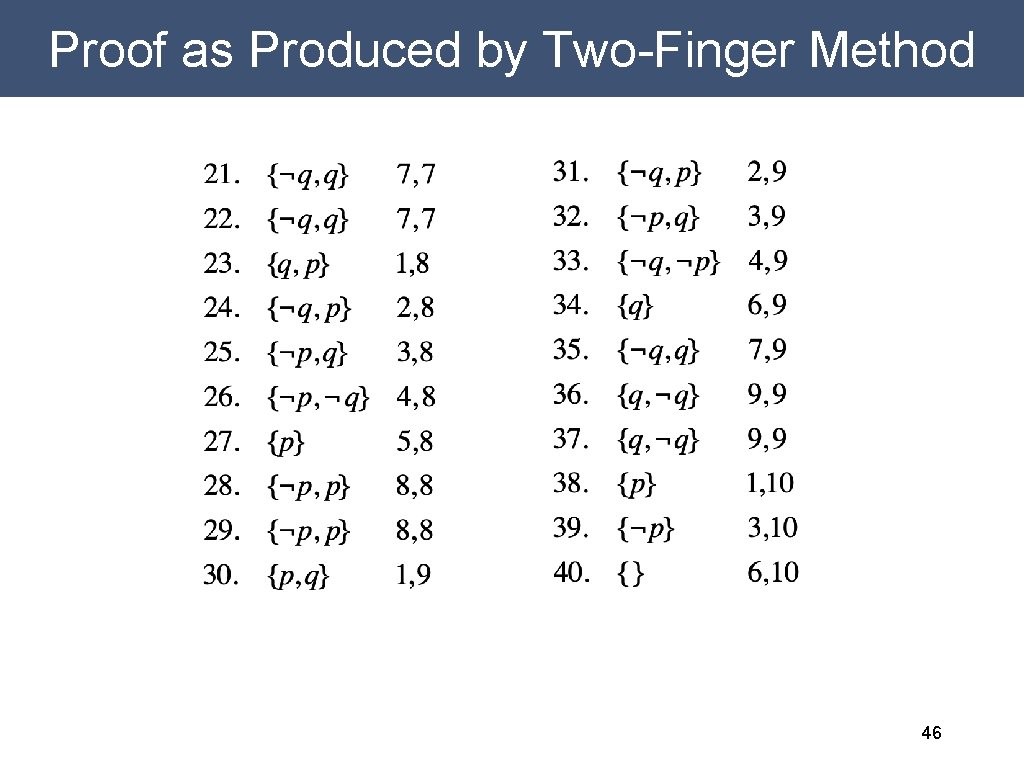
Proof as Produced by Two-Finger Method 45

Proof as Produced by Two-Finger Method 46

Identical Clause Elimination Metatheorem: There is a resolution refutation of D if and only if there is a resolution refutation from D in which no clause occurs twice. (Obvious. ) Upshot: If you generate a clause that is already in the proof, do not include it again. 47

Proof with Identical Clause Elimination 48

Motivation for Tautology Elimination 49

Tautology Elimination A tautology is a clause with a complementary pair of literals. {q, Øq} {p, q, r, Øq} Metatheorem: There is a resolution refutation of D if and only if there is a resolution refutation from D with tautology elimination. 50

Proof with ICE and TE 51

Motivation for Subsumption 52

Propositional Subsumption A clause F subsumes Y if and only if F is a subset of Y. Example: {p, q} subsumes {p, q, r} Theorem: There is a resolution refutation of D if and only if there is a resolution refutation from D with Propositional Subsumption. 53

Note The resolution of two clauses sometimes produces a clause that subsumes one of its parents. 54

Example of Pure Literal Elimination 55

Pure Literal Elimination A literal in a database is pure if and only if there is no complementary occurrence of the literal in the database. A clause is superfluous if and only if it contains a pure literal. Metatheorem: There is a resolution refutation of D if and only if there is a resolution refutation from D in which all superfluous clauses are removed. 56

Example 57

Note The removal of a superfluous clause may create new pure literals and new superfluous clauses. 58