Introduction to Logic Induction Michael Genesereth Computer Science

Induction is reasoning from the specific to the general. If various instances of a

Incomplete Induction Definition f(1) = 1 f(x + 1) = f(x) + 2*x +

Not So Lucky Guess Data: “Theorem” by Fermat (1601 -1665): Fact discovered (mercifully) after

Outline Domain Closure finite domains Linear Induction induction on sequences Tree Induction induction on

Finite Example f[a] f[b] f[c] f[d] "x. f[x]

Proof 1. p(a) Þ q(a) Premise 2. p(b) Þ q(b) Premise 3. p(c) Þ

Infinite Case What happens when we have infinitely many terms? p(a) Þ q(a) p(s(a))

Linear Languages Linearly Structured World: a ® s(a) ® s(s(a)) ® s(s(s(a))) ® …

Linear Induction f[a] "m. (f[m] Þ f[s(m)]) "u. f[u]

Linear Induction Base Case f[a] "m. (f[m] Þ f[s(m)]) "u. f[u]

Linear Induction Base Case f[a] "m. (f[m] Þ f[s(m)]) Inductive Case "u. f[u]

Linear Induction Inductive Hypothesis Base Case f[a] "m. (f[m] Þ f[s(m)]) Inductive Case "u.

Linear Induction Inductive Hypothesis Base Case Inductive Conclusion f[a] "m. (f[m] Þ f[s(m)]) Inductive

Dominoes Example Object constant: a Unary function constant: s Ternary relation constant: falls

Dominoes Example Object constant: a Unary function constant: s Ternary relation constant: falls Axioms:

Dominoes Proof 1. falls(a) Premise 2. "x. (falls(x) Þ falls(s(x))) Premise 3. "x. falls(x)

Arithmetic Example Object constant: 0 Unary function constant: s Ternary relation constant: plus

Arithmetic Example Object constant: 0 Unary function constant: s Ternary relation constant: plus Axioms

Arithmetic Proof 1. "y. plus(0, y, y) Premise 2. "x. "y. "z. (plus(x, y,

Tree Languages Tree-Like World: a f(a) f(f(a)) g(a) g(f(a)) f(g(a)) g(g(a)) Languages like this

Tree Induction f[a] "m. (f[m] Þ f[f(m)]) "m. (f[m] Þ f[g(m)]) "u. f[u]

Canine Ancestry Example Object constant: rex Unary function constants: f, g Unary relation constant:

Canine Example Canine Ancestry Example Object constant: rex Unary function constants: f, g Unary

Canine Ancestry Proof 1. p(rex) Premise 2. "x. (p(x) Û p(f(x)) Ù p(g(x))) Premise

General Languages Object constant: a, b Binary function constant: c Sample Terms a, c(a,

Structural Induction f[a] "l. "m. (f[l] Ù f[m] Þ f[c(l, m)]) "u. f[u]

Chemistry Example Object constant: 1, 2 Unary function constants: c Unary relation constant: a,

Chemistry Proof 1. a(1) Premise 2. a(2) Premise 3. "x. "y. (a(x) Ù a(y)

Chemistry Proof 7. a(1) Ú n(1) OI: 1 8. a(2) Ú n(2) OI: 2

Slides: 67

Download presentation

Introduction to Logic Induction Michael Genesereth Computer Science Department Stanford University

Induction is reasoning from the specific to the general. If various instances of a schema are true and there are no counterexamples, we are tempted to conclude a universally quantified version of the schema. p(a) Þ q(a) p(b) Þ q(b) p(c) Þ q(c) ® "x. p(x) Þ q(x)

Incomplete Induction Definition f(1) = 1 f(x + 1) = f(x) + 2*x + 1 Data Conjecture In this case, the answer is correct. Lucky Guess.

Not So Lucky Guess Data: “Theorem” by Fermat (1601 -1665): Fact discovered (mercifully) after his death: Oops.

Outline Domain Closure finite domains Linear Induction induction on sequences Tree Induction induction on trees Structural Induction induction on arbitrary structures

Domain Closure

General Form f 1[s] … fn[s] "u. f[u]

Finite Example f[a] f[b] f[c] f[d] "x. f[x]

Proof 1. p(a) Þ q(a) Premise 2. p(b) Þ q(b) Premise 3. p(c) Þ q(c) Premise 4. p(d) Þ q(d) Premise 5. "x. p(x) Þ q(x) Ind: 1 -4

Infinite Case What happens when we have infinitely many terms? p(a) Þ q(a) p(s(a)) Þ q(s(a)) p(s(s(a))) Þ q(s(s(a))) p(s(s(s(a)))) Þ q(s(s(s(a)))) … "x. p(x) Þ q(x)

Linear Induction

Linear Languages Linearly Structured World: a ® s(a) ® s(s(a)) ® s(s(s(a))) ® … Languages like this are called linear languages. The object constant in a linear language is called the base element, and the function constant is called the successor function.

Linear Induction f[a] "m. (f[m] Þ f[s(m)]) "u. f[u]

Linear Induction Base Case f[a] "m. (f[m] Þ f[s(m)]) "u. f[u]

Linear Induction Base Case f[a] "m. (f[m] Þ f[s(m)]) Inductive Case "u. f[u]

Linear Induction Inductive Hypothesis Base Case f[a] "m. (f[m] Þ f[s(m)]) Inductive Case "u. f[u]

Linear Induction Inductive Hypothesis Base Case Inductive Conclusion f[a] "m. (f[m] Þ f[s(m)]) Inductive Case "u. f[u] Overall Conclusion

Dominoes Set-up

Dominoes Example Object constant: a Unary function constant: s Ternary relation constant: falls

Dominoes Example Object constant: a Unary function constant: s Ternary relation constant: falls Axioms: falls(a) "x. (falls(x) Þ falls(s(x))

Dominoes Example Object constant: a Unary function constant: s Ternary relation constant: falls Axioms: falls(a) "x. (falls(x) Þ falls(s(x))) Goal: "x. falls(x)

Dominoes Proof 1. falls(a) Premise 2. "x. (falls(x) Þ falls(s(x))) Premise 3. "x. falls(x) Ind: 1, 2

Arithmetic Example Object constant: 0 Unary function constant: s Ternary relation constant: plus

Arithmetic Example Object constant: 0 Unary function constant: s Ternary relation constant: plus Axioms of Arithmetic: "y. plus(0, y, y) "x. "y. "z. (plus(x, y, z) Þ plus(s(x), y, s(z))

Arithmetic Example Object constant: 0 Unary function constant: s Ternary relation constant: plus Axioms of Arithmetic: "y. plus(0, y, y) "x. "y. "z. (plus(x, y, z) Þ plus(s(x), y, s(z)) Goal: "x. plus(x, 0, x)

Arithmetic Proof 1. "y. plus(0, y, y) Premise 2. "x. "y. "z. (plus(x, y, z) Þ plus(s(x), y, s(z)) Premise

Arithmetic Proof 1. "y. plus(0, y, y) Premise 2. "x. "y. "z. (plus(x, y, z) Þ plus(s(x), y, s(z)) Premise 3. plus(0, 0, 0) UE: 1

Arithmetic Proof 1. "y. plus(0, y, y) Premise 2. "x. "y. "z. (plus(x, y, z) Þ plus(s(x), y, s(z)) Premise 3. plus(0, 0, 0) UE: 1 4. plus(x, 0, x) Assumption

Arithmetic Proof 1. "y. plus(0, y, y) Premise 2. "x. "y. "z. (plus(x, y, z) Þ plus(s(x), y, s(z)) Premise 3. plus(0, 0, 0) UE: 1 4. plus(x, 0, x) Assumption 5. plus(x, 0, x) Þ plus(s(x), 0, s(x)) 3 x UE: 2 6. plus(s(x), 0, s(x)) IE: 2, 4 7. plus(x, 0, x) Þ plus(s(x), 0, s(x)) II: 4, 6

Tree Induction

Tree Languages Tree-Like World: a f(a) f(f(a)) g(a) g(f(a)) f(g(a)) g(g(a)) Languages like this are called tree languages.

Tree Induction f[a] "m. (f[m] Þ f[f(m)]) "m. (f[m] Þ f[g(m)]) "u. f[u]

Canine Ancestry Example Object constant: rex Unary function constants: f, g Unary relation constant: p

Canine Ancestry Example Object constant: rex Unary function constants: f, g Unary relation constant: p Axiom: "x. (p(x) Û p(f(x)) Ù p(g(x)))

Canine Example Canine Ancestry Example Object constant: rex Unary function constants: f, g Unary relation constant: p Axioms: p(rex) "x. (p(x) Û p(f(x)) Ù p(g(x))) Goal: "x. p(x)

Canine Ancestry Proof 1. p(rex) Premise 2. "x. (p(x) Û p(f(x)) Ù p(g(x))) Premise

Canine Ancestry Proof 1. p(rex) Premise 2. "x. (p(x) Û p(f(x)) Ù p(g(x))) Premise 3. p(x) Û p(f(x)) Ù p(g(x)) UE: 2 4. p(x) Þ p(f(x)) Ù p(g(x)) BE: 3

Canine Ancestry Proof 1. p(rex) Premise 2. "x. (p(x) Û p(f(x)) Ù p(g(x))) Premise 3. p(x) Û p(f(x)) Ù p(g(x)) UE: 2 4. p(x) Þ p(f(x)) Ù p(g(x)) BE: 3 5. p(x) Assumption

Canine Ancestry Proof 1. p(rex) Premise 2. "x. (p(x) Û p(f(x)) Ù p(g(x))) Premise 3. p(x) Û p(f(x)) Ù p(g(x)) UE: 2 4. p(x) Þ p(f(x)) Ù p(g(x)) BE: 3 5. p(x) Assumption 6. p(f(x)) Ù p(g(x)) IE: 4, 5

Canine Ancestry Proof 1. p(rex) Premise 2. "x. (p(x) Û p(f(x)) Ù p(g(x))) Premise 3. p(x) Û p(f(x)) Ù p(g(x)) UE: 2 4. p(x) Þ p(f(x)) Ù p(g(x)) BE: 3 … 9. "x. (p(x) Þ p(f(x))) UI: 8 … 14. "x. (p(x) Þ p(g(x))) UI: 13 15. "x. p(x) Ind: 1, 9, 14

Structural Induction

General Languages Object constant: a, b Binary function constant: c Sample Terms a, c(a, a), c(a, b), c(b, a), c(b, b), c(a, a)), …

Structural Induction f[a] "l. "m. (f[l] Ù f[m] Þ f[c(l, m)]) "u. f[u]

Chemistry Set-up

Demonstration

Chemistry Example Object constant: 1, 2 Unary function constants: c Unary relation constant: a, n, b

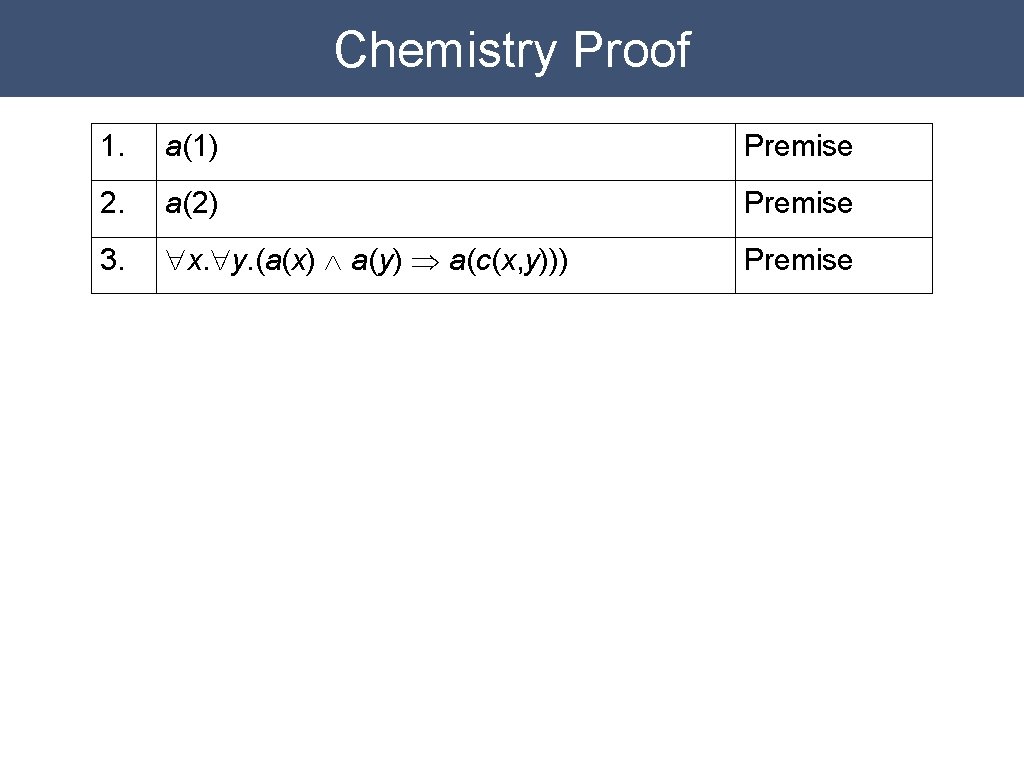
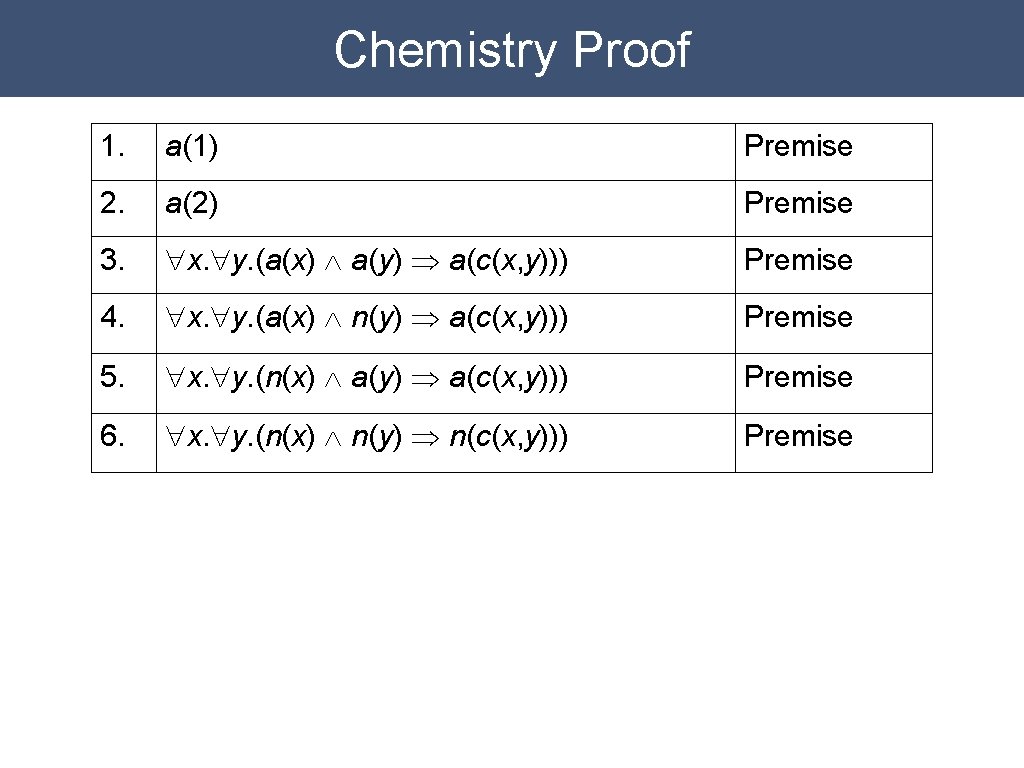
Chemistry Example Object constant: 1, 2 Unary function constants: c Unary relation constant: a, n, b Axioms: "x. (a(x) Ù a(y) Þ a(c(x, y))) "x. (b(x) Ù b(y) Þ b(c(x, y))) "x. (a(x) Ù n(y) Þ a(c(x, y))) "x. (b(x) Ù n(y) Þ b(c(x, y))) "x. (n(x) Ù a(y) Þ a(c(x, y))) "x. (n(x) Ù b(y) Þ b(c(x, y))) "x. (n(x) Ù n(y) Þ n(c(x, y)))

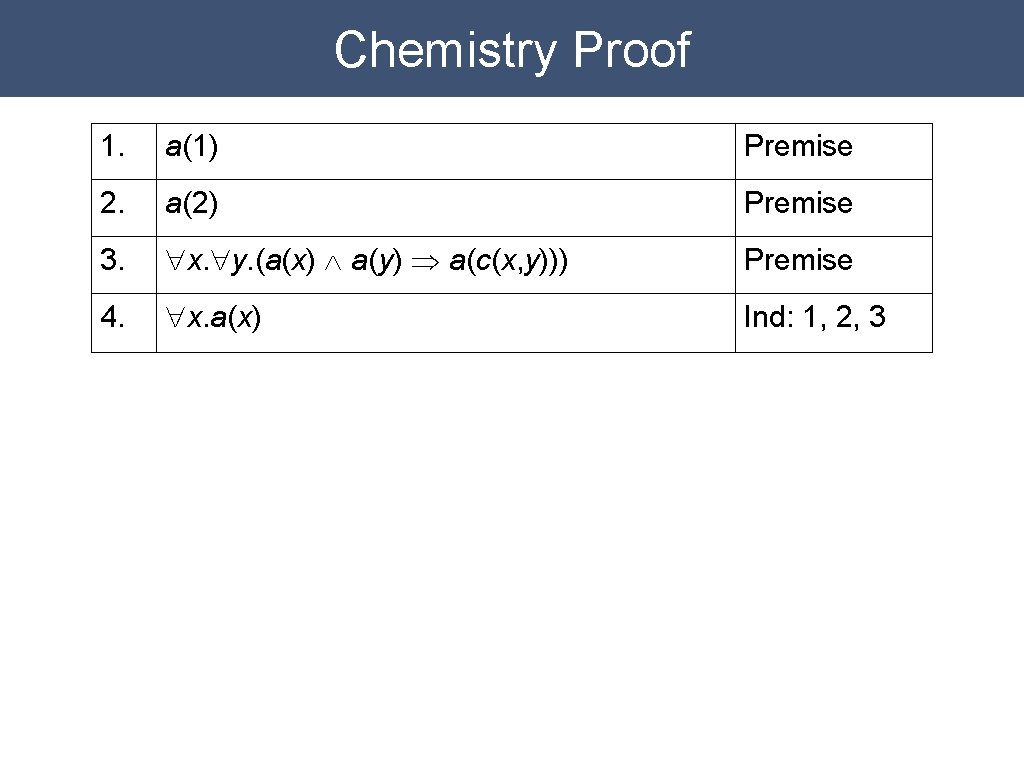
Chemistry Proof 1. a(1) Premise 2. a(2) Premise 3. "x. "y. (a(x) Ù a(y) Þ a(c(x, y))) Premise

Chemistry Proof 1. a(1) Premise 2. a(2) Premise 3. "x. "y. (a(x) Ù a(y) Þ a(c(x, y))) Premise 4. "x. a(x) Ind: 1, 2, 3

Chemistry Proof 1. a(1) Premise 2. a(2) Premise 3. "x. "y. (a(x) Ù a(y) Þ a(c(x, y))) Premise 4. "x. "y. (a(x) Ù n(y) Þ a(c(x, y))) Premise 5. "x. "y. (n(x) Ù a(y) Þ a(c(x, y))) Premise 6. "x. "y. (n(x) Ù n(y) Þ n(c(x, y))) Premise

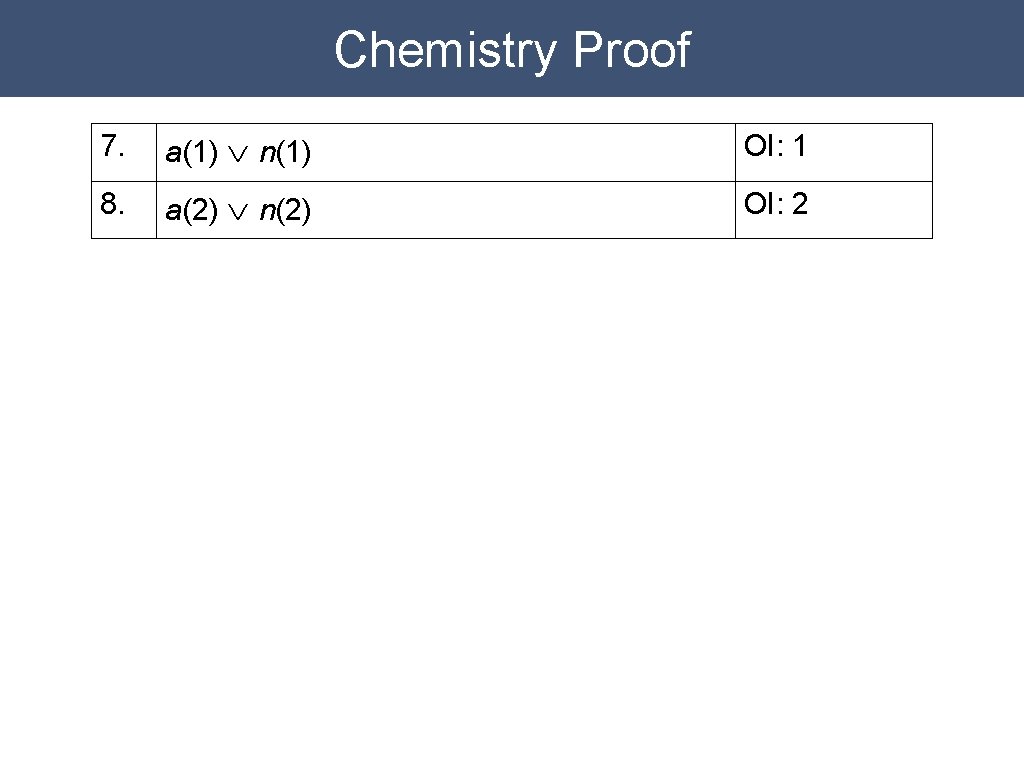
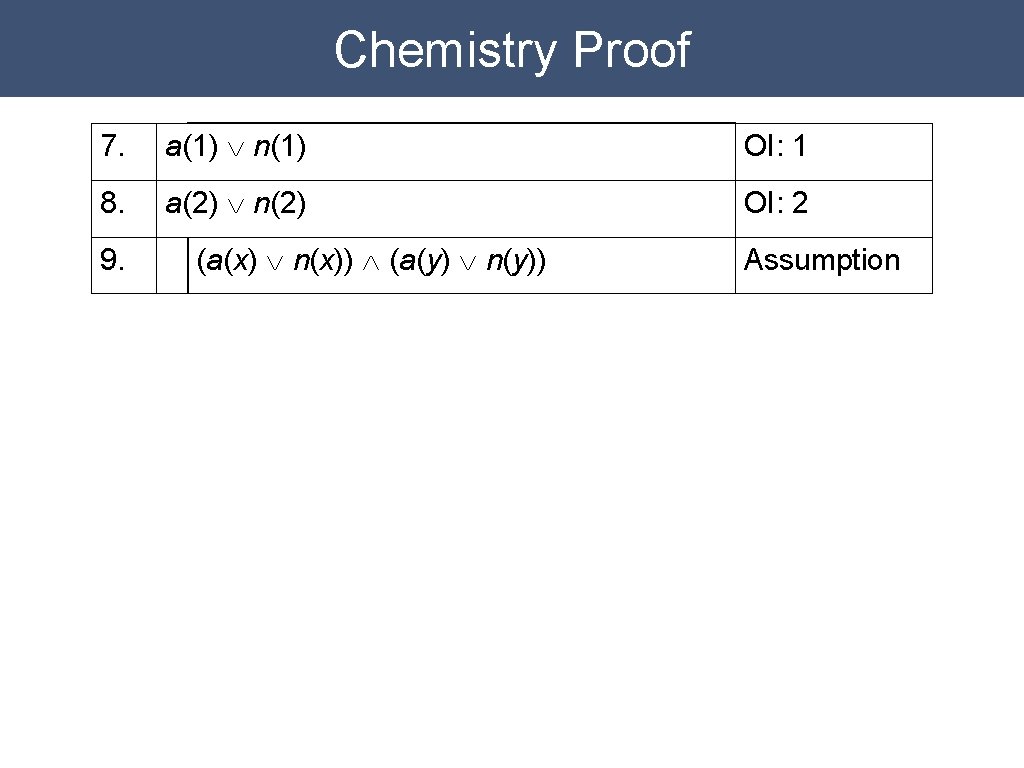
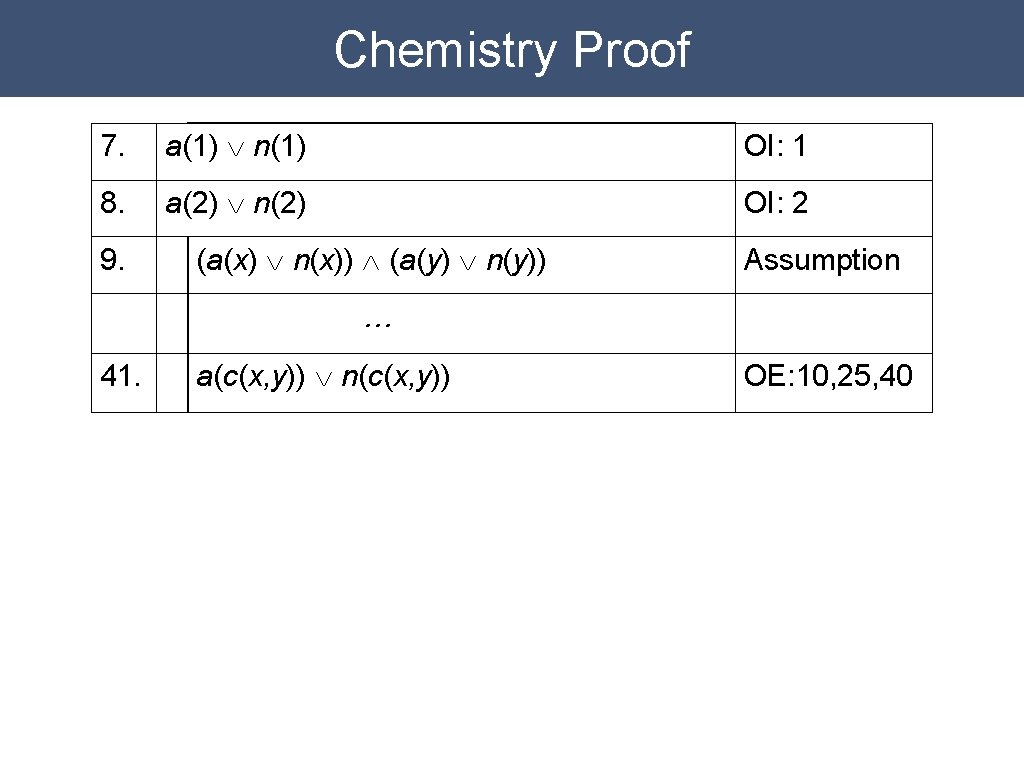
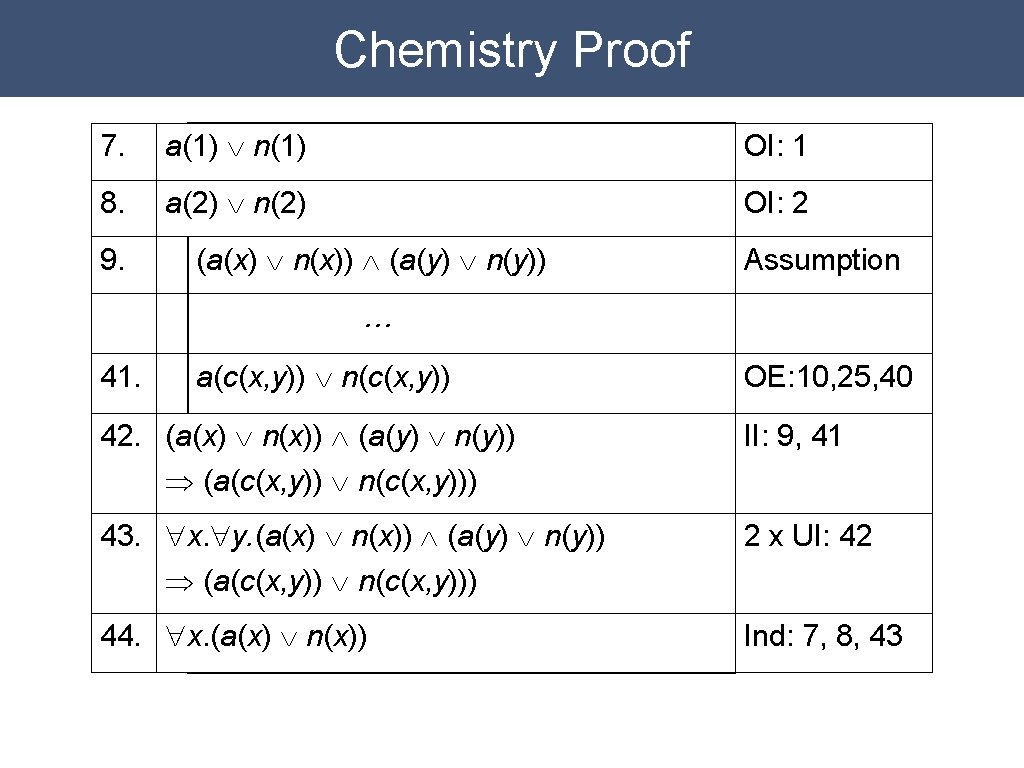
Chemistry Proof 7. a(1) Ú n(1) OI: 1 8. a(2) Ú n(2) OI: 2

Chemistry Proof 7. a(1) Ú n(1) OI: 1 8. a(2) Ú n(2) OI: 2 9. (a(x) Ú n(x)) Ù (a(y) Ú n(y)) Assumption

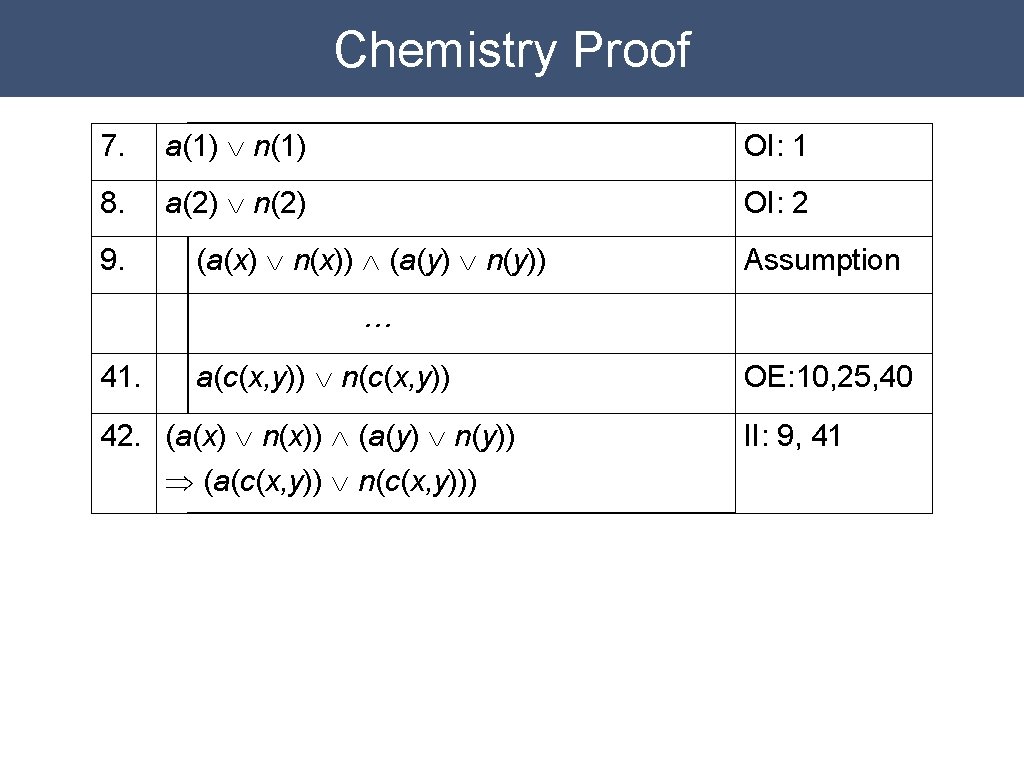
Chemistry Proof 7. a(1) Ú n(1) OI: 1 8. a(2) Ú n(2) OI: 2 9. (a(x) Ú n(x)) Ù (a(y) Ú n(y)) Assumption … 41. a(c(x, y)) Ú n(c(x, y)) OE: 10, 25, 40

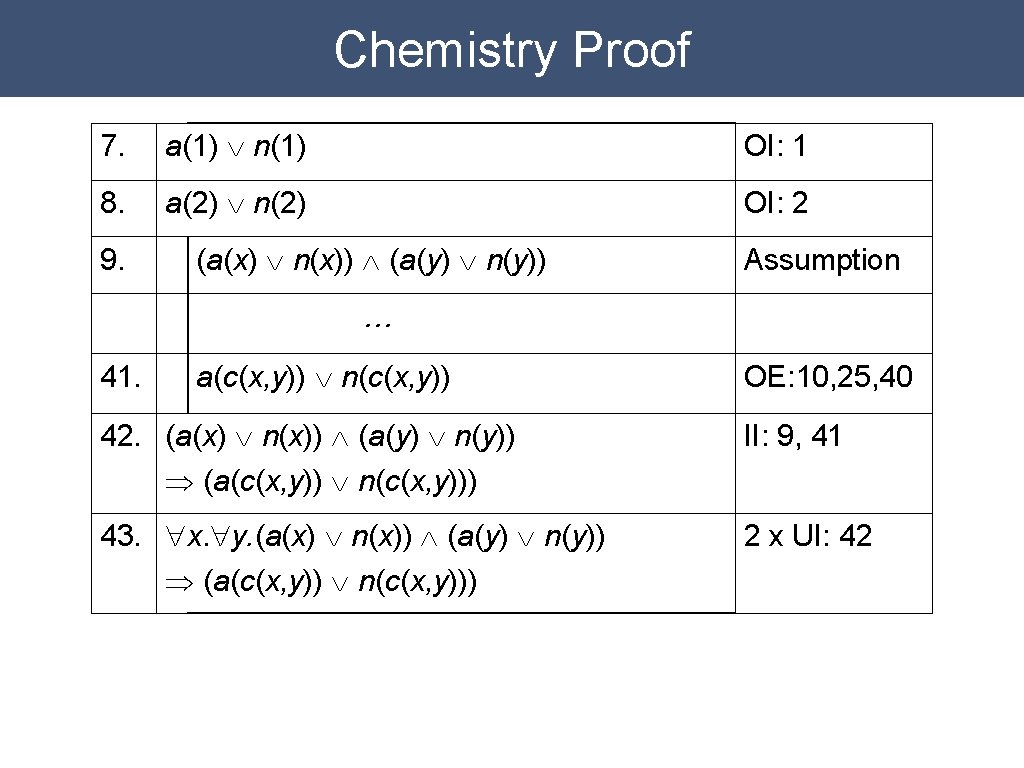
Chemistry Proof 7. a(1) Ú n(1) OI: 1 8. a(2) Ú n(2) OI: 2 9. (a(x) Ú n(x)) Ù (a(y) Ú n(y)) Assumption … 41. a(c(x, y)) Ú n(c(x, y)) 42. (a(x) Ú n(x)) Ù (a(y) Ú n(y)) Þ (a(c(x, y)) Ú n(c(x, y))) OE: 10, 25, 40 II: 9, 41

Chemistry Proof 7. a(1) Ú n(1) OI: 1 8. a(2) Ú n(2) OI: 2 9. (a(x) Ú n(x)) Ù (a(y) Ú n(y)) Assumption … 41. a(c(x, y)) Ú n(c(x, y)) OE: 10, 25, 40 42. (a(x) Ú n(x)) Ù (a(y) Ú n(y)) Þ (a(c(x, y)) Ú n(c(x, y))) II: 9, 41 43. "x. "y. (a(x) Ú n(x)) Ù (a(y) Ú n(y)) Þ (a(c(x, y)) Ú n(c(x, y))) 2 x UI: 42