Introduction to Logarithms By Abe E Logba Mathematical

Introduction to Logarithms By Abe E. Logba

Mathematical Uses of logarithms • • • Calculate numbers raised to any power Calculate roots of a number Simplify complex computations Solve certain equations Take derivative of a complex function

More Uses of Logarithms • • Chemistry - p. H measurements Biology - population growth Music - logarithmic representation of frequency Physics - entropy calculations Astronomy - stellar masses vs. helium burnings Number Theory - discrete logarithm problem Economics - Deregulation, profit, cost in banking Pharmacy - pharmacological response vs. dose

Definition of Logarithm • Definition: Let b > 0, and b ≠ 1, and x = by. Then y is the logarithm of x (base b). That is, x = by means that y = logb x. NOTE: Make sure that x > 0

To remember the conversion x = by <=> y = logb x. Just remember the expert. . . ABE E. LOGBA A = BE <=> E = LOGB A A - Argument B - Base E - Exponent

Exponential Equations vs Logarithmic Equations Exponential Equation Logarithmic Equation • 52 = 25 • log 5 25 = 2 • 2– 3 = 1/8 • log 2 (1/8) = – 3 • 104 = 10, 000 • log 10000 = 4 • ln 1 = 0 • e 0 = 1

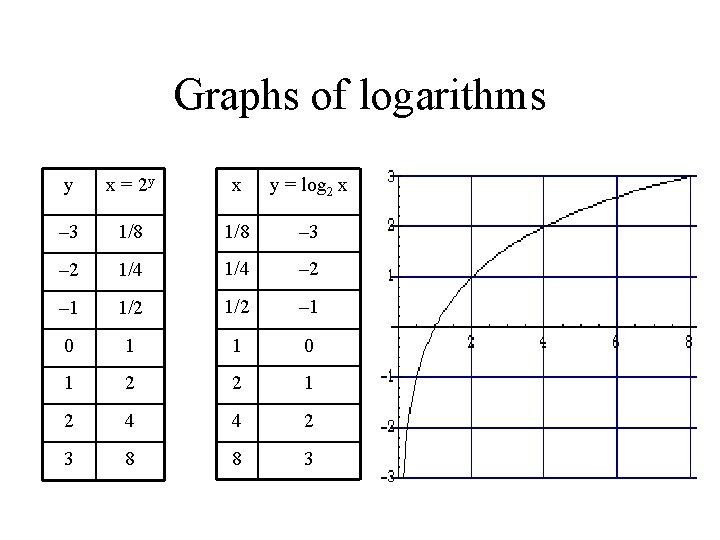
Graphs of logarithms y x = 2 y x y = log 2 x – 3 1/8 – 3 – 2 1/4 – 2 – 1 1/2 – 1 0 1 2 2 1 2 4 4 2 3 8 8 3

Four Logarithm Graphs • A -> y = log 2(x) • B -> y = log 3(x) • C -> y = log 5(x) • D -> y = log 10(x)

• Two special logarithm bases have special designations. They are common logarithms (base 10) and natural logarithms (base e). Base We Write We Mean base 10 log x log 10 x base e ln x loge x • Note: Sometimes we simply write logb x, but the meaning is always logb (x), since we are using a function with argument x. If there is any confusion about the argument, then use parentheses.

Various Logarithm Graphs

Properties of Logarithms • All of these properties come from the definition of logarithms and the properties of exponents. • All bases are assumed to be feasible (positive but not equal to 1). • You must memorize these properties! • You must know how to use these properties forwards and backwards!

Two Basic Properties • logb 1 = 0 • log 1 = 0, ln 1 = 0, log 5 1 = 0 • logb b = 1 • log 10 = 1, ln e = 1, log 2 2 = 1

Three Algebraic Properties

Two Inverse Properties

Change of Base • Calculators and computers typically only use logarithms with base e and base 10. It is possible to convert a logarithm from another base (b) to your desired base (e or 10) using the change of base formula.

Logarithmic Example Table for Common Logarithms

Solving Equations with Logarithms • For b > 0, b ≠ 1, and x > 0 and y > 0, we get two important logarithmic properties. 1) If x = y, then logb x = logb y 2) If logb x = logb y, then x = y. • The argument of a logarithm is always positive. When you solve equations with logarithms, you should always check your answer!

Consider Using Logarithms To Solve Equations When You Have • An exponential function on a side by itself • One logarithm on one side by itself • One logarithm on each side (with the same base) by itself

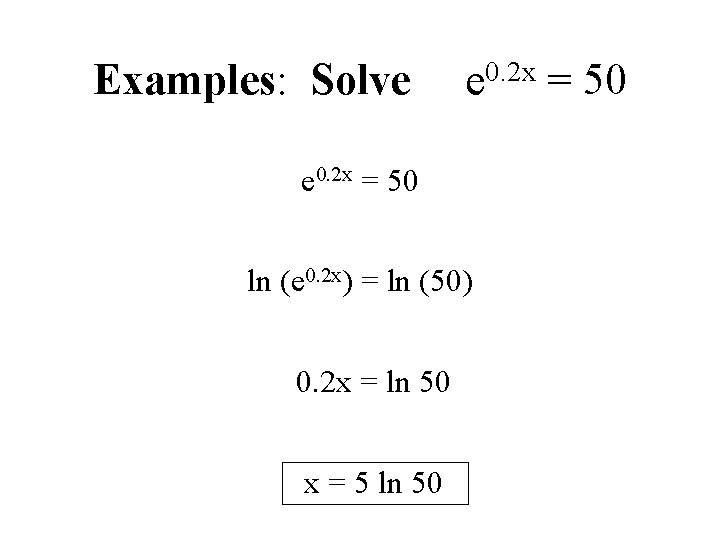
Examples: Solve e 0. 2 x = 50 ln (e 0. 2 x) = ln (50) 0. 2 x = ln 50 x = 5 ln 50

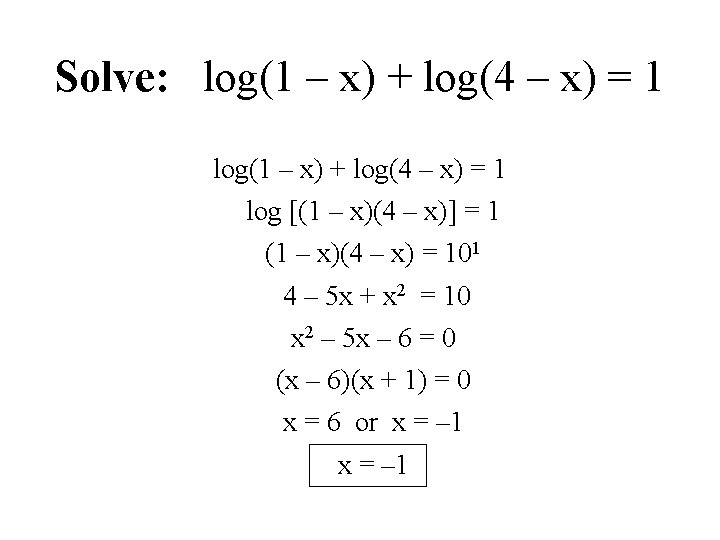
Solve: log(1 – x) + log(4 – x) = 1 log [(1 – x)(4 – x)] = 1 (1 – x)(4 – x) = 101 4 – 5 x + x 2 = 10 x 2 – 5 x – 6 = 0 (x – 6)(x + 1) = 0 x = 6 or x = – 1

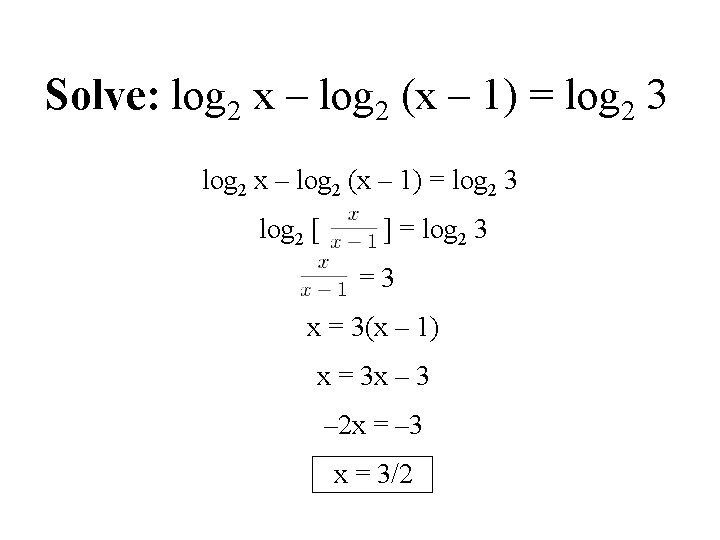
Solve: log 2 x – log 2 (x – 1) = log 2 3 log 2 [ ] = log 2 3 =3 x = 3(x – 1) x = 3 x – 3 – 2 x = – 3 x = 3/2