Introduction to Language Theory Programming Language Translators Prepared

Introduction to Language Theory Programming Language Translators Prepared by Manuel E. Bermúdez, Ph. D. Associate Professor University of Florida

Introduction to Language Theory Definition: An alphabet (or vocabulary) Σ is a finite set of symbols. Example: Alphabet of Pascal: +-*/<… (operators) begin end if var (keywords) <identifier> (identifiers) <string> (strings) <integer> (integers) ; : , ()[] (punctuators) Note: All identifiers are represented by one symbol, because Σ must be finite.

Introduction to Language Theory Definition: A sequence t = t 1 t 2…tn of symbols from an alphabet Σ is a string. Definition: The length of a string t = t 1 t 2…tn (denoted |t|) is n. If n = 0, the string is ε, the empty string. Definition: Given strings s = s 1 s 2…sn and t = t 1 t 2…tm, the concatenation of s and t, denoted st, is the string s 1 s 2…snt 1 t 2…tm.

Introduction to Language Theory Note: εu = uε, uεv = uv, for any strings u, v (including ε) Definition: Σ* is the set of all strings of symbols from Σ. Note: Σ* is called the reflexive, transitive closure of Σ. Σ* is described by the graph (Σ*, ·), where “·” denotes concatenation, and there is a designated “start” node, ε.

Introduction to Language Theory Example: Σ = {a, b}. (Σ*, ·) a a a ε b aa b aba abb ba b bb Σ* is countably infinite, so can’t compute all of Σ*, and can only compute finite subsets of Σ*, but can compute whether a given string is in Σ*.

Introduction to Language Theory Example: Σ = Pascal vocabulary. Σ* = all possible alleged Pascal programs, i. e. all possible inputs to Pascal compiler. Need to specify L Σ*, the correct Pascal programs. Definition: A language L over an alphabet Σ is a subset of Σ*.

Introduction to Language Theory Example: Σ = {a, b}. L 1 = ø is a language L 2 = {ε} is a language L 3 = {a} is a language L 4 = {a, bbab} is a language L 5 = {anbn / n >= 0} is a language where an = aa…a, n times L 6 = {a, aaa, …} is a language Note: L 5 is an infinite language, but described finitely.

Introduction to Language Theory THIS IS THE MAIN GOAL OF LANGUAGE SPECIFICATION : To describe (infinite) programming languages finitely, and to provide corresponding finite inclusion-test algorithms.

Language Constructors Definition: The catenation (or product) of two languages L 1 and L 2, denoted L 1 L 2, is the set {uv | u L 1, v L 2}. Example: L 1 = {ε, a, bb}, L 2 = {ac, c} L 1 L 2 = {ac, c, aac, bbac, bbc} = {ac, c, aac, bbc}

Language Constructors Definition: Ln = LL…L (n times), and L 0 = {ε}. Example: L = {a, bb} L 3 = {aaa, aabb, abba, abbbb, bbaa, bbabb, bbbba, bbbbbb}

Language Constructors Definition: The union of two languages L 1 and L 2 is the set L 1 L 2 = {u | u L 1} { v | v L 2} ∩ ∩ Definition: The Kleene star (L*) of a language is the set L* = U Ln, n >0. Example: L = {a, bb} L* = {any string composed of a’s and bb’s} Definition: The Transitive Closure (L+) of a language L is the set L+ = U Ln, n > 1.

Language Constructors Note: In general, L* = L+ U {ε}, but L+ ≠ L* - {ε}. For example, consider L = {ε}. Then {ε} = L+ ≠ L* – {ε} = {ε} – {ε} = ø.

Grammars Goal: Providing a means for describing languages finitely. Method: Provide a subgraph (Σ*, →*) of (Σ*, ·), and a start node S, such that the set of reachable nodes (from S) are the strings in the language.

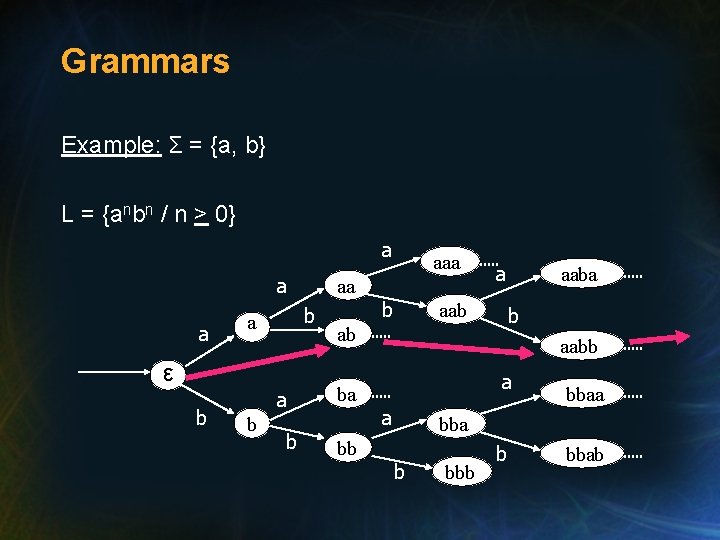
Grammars Example: Σ = {a, b} L = {anbn / n > 0} a a a ε b a b aaa b aab ab a aaba b aabb a ba a bb b bbaa bbb b bbab

Grammars “=>” (derives) is a relation defined by a finite set of rewrite rules known as productions. Definition: Given a vocabulary V, a production is a pair (u, v) V* x V*, denoted u → v. u is called the left-part; v is called the right-part.

Grammars Example: Pseudo-English. V = {Sentence, NP, VP, Adj, N, V, boy, girl, the, tall, jealous, hit, bit} Sentence NP NP N N Adj Adj VP V V → → → NP VP N Adj NP boy girl the tall jealous V NP hit bit (one production) Note: English is much too complicated to be described this way.

Grammars Definition: Given a finite set of productions P V* x V* the relation => is defined such that , β, u, v V* , uβ => vβ iff u → v P is a production. Example: Sentence NP NP N N → → → NP VP N Adj NP boy girl Adj Adj VP V V → → → the tall jealous V NP hit bit

Grammars Sentence => => => => NP Adj the the the VP NP VP Adj NP jealous jealous jealous VP NP VP N VP girl V NP girl hit Adj girl hit the NP NP N boy

Grammars Definition: A grammar is a 4 -tuple G = (Φ, Σ, P, S) where Φ is a finite set of nonterminals, Σ is a finite set of terminals, V = Φ U Σ is the grammar’s vocabulary, S Φ is called the start or goal symbol, and P V* x V* is a finite set of productions. Example: Grammar for {anbn / n > 0}. G = (Φ, Σ, P, S), where Φ = {S}, Σ = {a, b}, and P = {S → a. Sb, S → ε}

Grammars aaabbb => aabb => ab => ε => => Derivations: S => a. Sb => aa. Sbb => aaa. Sbbb => aaaa. Sbbbb → … aaaabbbb Note: Normally, grammars are given by simply listing the productions.

Grammar Conventions TWS convention 1. 2. 3. 4. Upper case letter (identifier) – nonterminal Lower case letter (string) – terminal Lower case greek letter – strings in V* Left part of the first production is assumed to be the start symbol, e. g. S → a. Sb S→ε 5. Left part omitted if same as for preceeding production, e. g. S → a. Sb →ε

Grammars Example: Grammar for identifiers. Identifier Letter Digit → → →. . → Letter Identifier Digit ‘a’ → ‘A’ ‘b’ → ‘B’ ‘z’ → ‘Z’ ‘ 0’ ‘ 1’ ‘ 9’

Grammars Definition: The language generated by a grammar G, is the set L(G) = { Σ* | S =>* } Definition: A sentential form generated by a grammar G is any string α such that S =>* . Definition: A sentence generated by a grammar G is any sentential form such that Σ*.

Grammars Example: sentential forms S => a. Sb => aa. Sbb => aaa. Sbbb => aaaa. Sbbbb > … aaabbb sentences Lemma: L(G) = { | is a sentence} Proof: Trivial. => aabb => ab => => => ε aaaabbbb

Grammars Example: A → a. ABC → a. BC a. B → ab b. B → bb b. C → bc CB → BC c. C → cc

Grammars => a. ABC => aa. ABCBC aab. CBC abc aab. BCC => => aabbc. C aaab. BBCCC (2) aaabbb. CCC => => aabbcc aaa. BBBCCC => => => aabb. CC aaa. BBCBCC => ab. C aaa. BCBCBC => aa. BCBC => a. BC => => => Derivations: A => aaabbbc. CC (2) aaabbbccc L (G) = {anbncn | n > 1} => …

The Chomsky Hierarchy A hierarchy of grammars, the languages they generate, and the machines the accept those languages.

The Chomsky Hierarchy Type Language Name Grammar Name Restrictions Accepting On grammar Machine 0 Recursively Enumerable Unrestricted re-writing system None 1 Context-Sensitive Language Context. Sensitive Grammar For all → , Linear Bounded | |≤| | Automaton 2 Context- Free Language Context. Free Grammar For all → , Push-Down Automaton Φ. (parser) 3 Regular Language Regular Grammar For all → , Finite- State Φ, U Automaton ΦU{ } Turing Machine

Language Hierarchy 0: Recursively Enumerable Languages 1: Context-Sensitive Languages 2: Context-free Languages 3: Regular Languages {an | n > 0} {anbn | n>0} {anbncn | n>0} English? We will deal with type 2 (syntax) and type 3 (lexicon) languages.