Introduction to Krylov Subspace Methods DEF Krylov sequence

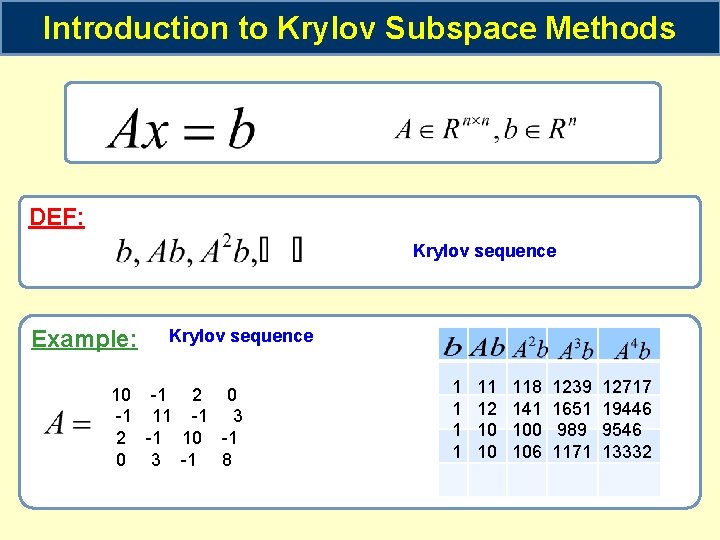
Introduction to Krylov Subspace Methods DEF: Krylov sequence Example: Krylov sequence 10 -1 2 0 -1 11 -1 3 2 -1 10 -1 0 3 -1 8 1 1 11 12 10 10 118 141 100 106 1239 1651 989 1171 12717 19446 9546 13332

Introduction to Krylov Subspace Methods DEF: Krylov subspace Example: Krylov subspace 10 -1 2 0 -1 11 -1 3 2 -1 10 -1 0 3 -1 8 Remark:

WHY: Krylov Subspace Methods Example: Solve: 10 -1 2 0 -1 11 -1 3 2 -1 10 -1 0 3 -1 8 >> A=[10 -1 2 0; -1 11 -1 3; 2 -1 10 -1; 0 3 -1 8] >> poly(A) 1 -39 552 -3357 7395 Hence, Characteristic poly the Cayley-Hamilton theorem a matrix satisfies its characteristic polynomial, p(A) = 0. That is, Multiplying with inv(A) & rearrange The key observation here is that the solution x to Ax = b is a linear combination of the vectors b and Ab, . . which make up the Krylov subspace the solution to Ax = b has a natural representation as a member of a Krylov space,

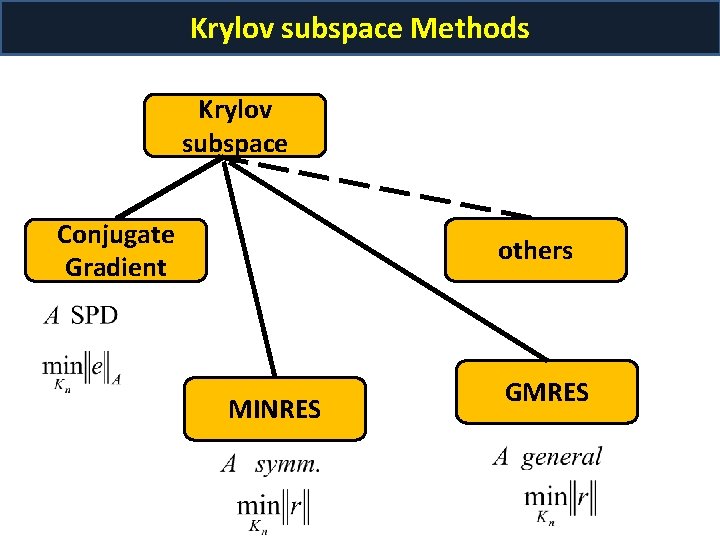
Krylov subspace Methods Krylov subspace Conjugate Gradient others MINRES GMRES

MATLAB commands Conjugate Gradient x = pcg(A, b, tol, maxit) MINRES x = minres(A, b, tol, maxit) GMRES x = gmres(A, b, [], tol, maxit)

Conjugate Gradient Method We want to solve the following linear system Conjugate Gradient Method

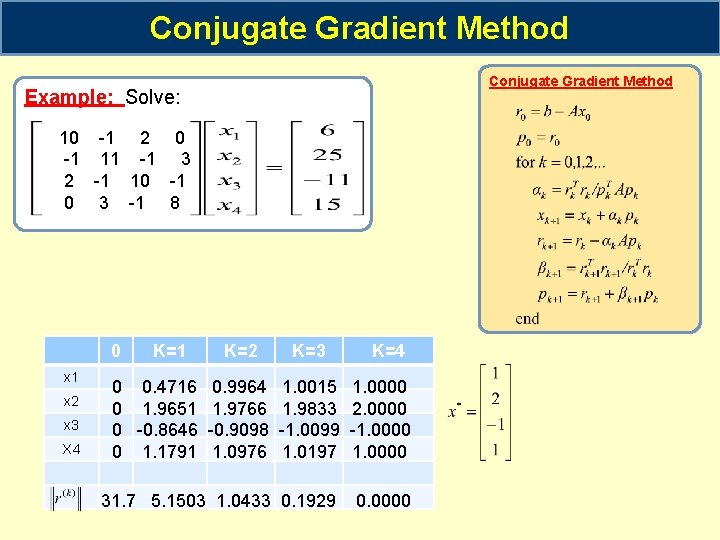
Conjugate Gradient Method Example: Solve: 10 -1 2 0 -1 11 -1 3 2 -1 10 -1 0 3 -1 8 0 x 1 x 2 x 3 X 4 K=1 K=2 0 0. 4716 0. 9964 0 1. 9651 1. 9766 0 -0. 8646 -0. 9098 0 1. 1791 1. 0976 K=3 K=4 1. 0015 1. 9833 -1. 0099 1. 0197 1. 0000 2. 0000 -1. 0000 31. 7 5. 1503 1. 0433 0. 1929 0. 0000