Introduction to Intensive Longitudinal Data and Common MixedModeling

Introduction to Intensive Longitudinal Data and Common Mixed-Modeling Techniques Summer Frank-Pearce, Ph. D, MPH University of Oklahoma Health Sciences Center 2019 Joint Statistical Meetings, Denver CO Supported by American Cancer Society (PI: Businelle; MRSGT-12 -114 -01 -CPPB) and Oklahoma Tobacco Settlement Endowment Trust (092 -016 -0002 l)

What are Intensive Longitudinal Data (ILD)? • Data from repeated measurements on same individual • ~30 or more measurements • In real-time • In natural environment • Common terms for method of collecting ILD • Experience Sampling • Ecological Momentary Assessments (EMA) 2

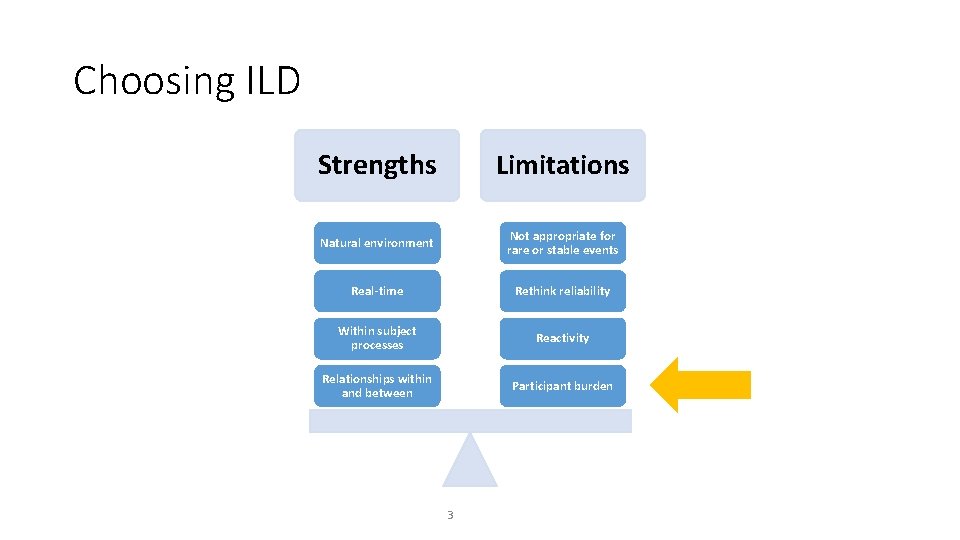
Choosing ILD Strengths Limitations Natural environment Not appropriate for rare or stable events Real-time Rethink reliability Within subject processes Reactivity Relationships within and between Participant burden 3

A Limitation of ILD • Participant burden • 5 EMA X 7 days X 5 weeks = 175 observations/person • 2 minute EMA -> more than 5 hours • 3 minute EMA -> more than 8 hours • Large amount of data produced • 175 X 150 = 26, 250 total observations • Storing capacity, server space • Data processing and manipulation slower 4

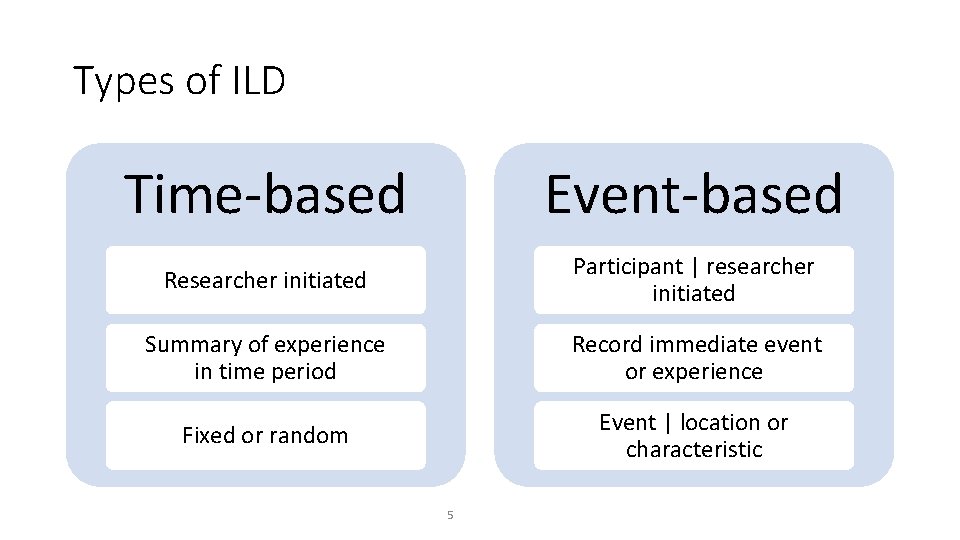
Types of ILD Time-based Event-based Researcher initiated Participant | researcher initiated Summary of experience in time period Record immediate event or experience Fixed or random Event | location or characteristic 5

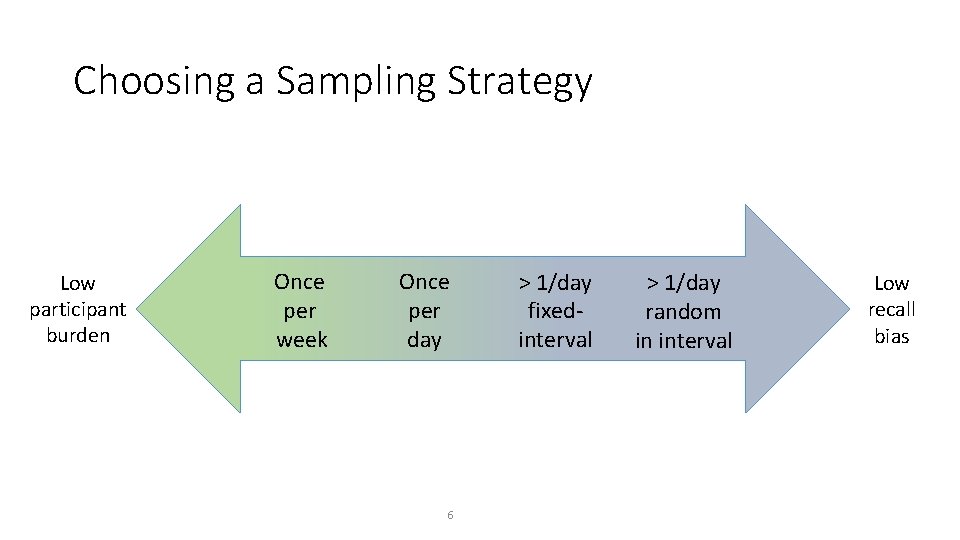
Choosing a Sampling Strategy Low participant burden Once per week Once per day 6 > 1/day fixedinterval > 1/day random in interval Low recall bias

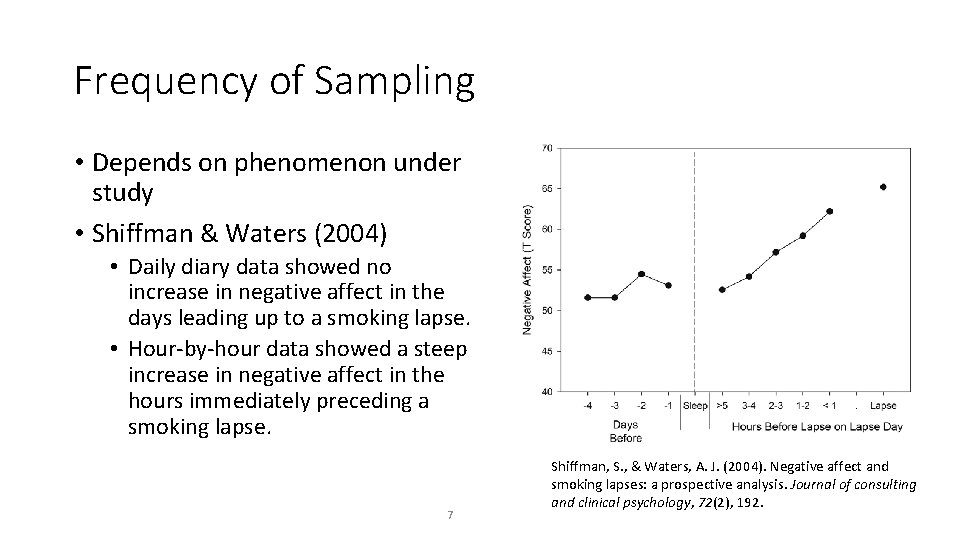
Frequency of Sampling • Depends on phenomenon under study • Shiffman & Waters (2004) • Daily diary data showed no increase in negative affect in the days leading up to a smoking lapse. • Hour-by-hour data showed a steep increase in negative affect in the hours immediately preceding a smoking lapse. 7 Shiffman, S. , & Waters, A. J. (2004). Negative affect and smoking lapses: a prospective analysis. Journal of consulting and clinical psychology, 72(2), 192.

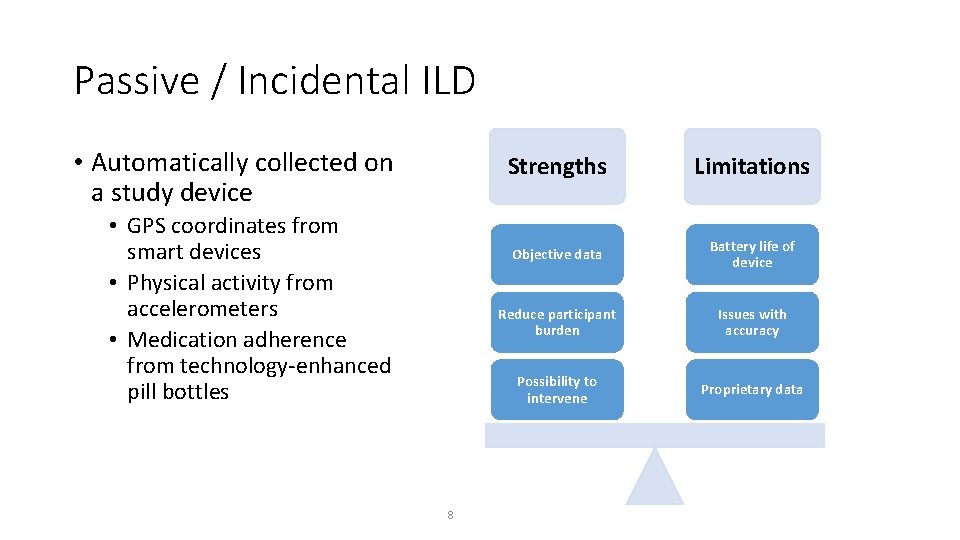
Passive / Incidental ILD • Automatically collected on a study device • GPS coordinates from smart devices • Physical activity from accelerometers • Medication adherence from technology-enhanced pill bottles 8 Strengths Limitations Objective data Battery life of device Reduce participant burden Issues with accuracy Possibility to intervene Proprietary data

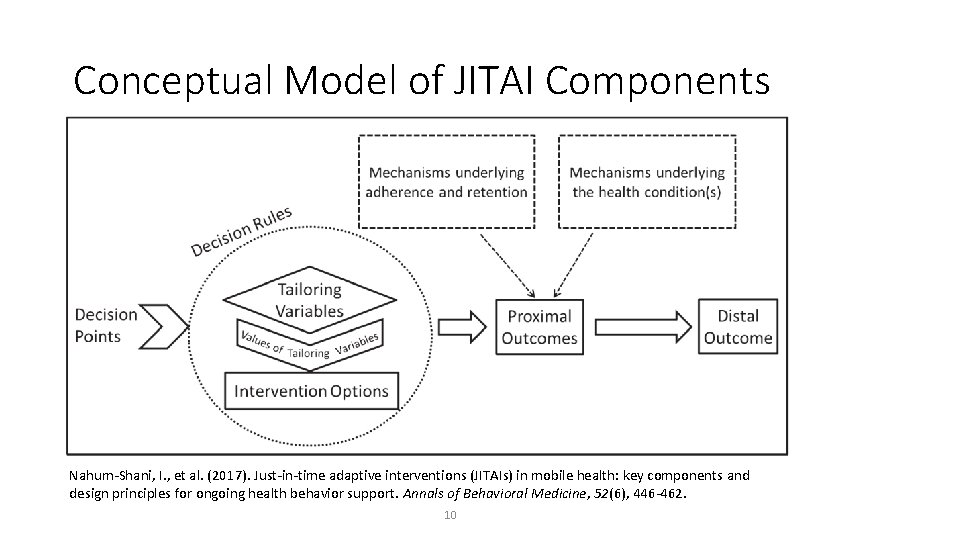
Just-in-Time Adaptive Interventions (JITAI) • Tailored support delivered via mobile technology in the moments when it is most needed • Treatment messages, audio, video • Can be tailored to environmental cues, mood, personal factors • Require decision rules for when to deliver treatment. 9

Conceptual Model of JITAI Components Nahum-Shani, I. , et al. (2017). Just-in-time adaptive interventions (JITAIs) in mobile health: key components and design principles for ongoing health behavior support. Annals of Behavioral Medicine, 52(6), 446 -462. 10

Smart-T Study • Aim • To evaluate the efficacy of an adjunctive, tailored, smart phone based smoking cessation application for smokers at tobacco cessation clinic • Method • Carry smart phone that delivers treatment for 3 weeks • 1 week pre-quit • 2 weeks post-quit • 5 EMAs per day 11

Smart-T Risk Algorithm • Uses EMA responses to assess current risk of smoking lapse • Just-in-time intervention (JITAI) • Risk level dictates appropriate tailored message • Urge, stress, motivation, cigarette availability • Tailored message automatically pushed to help participants avoid lapse 12

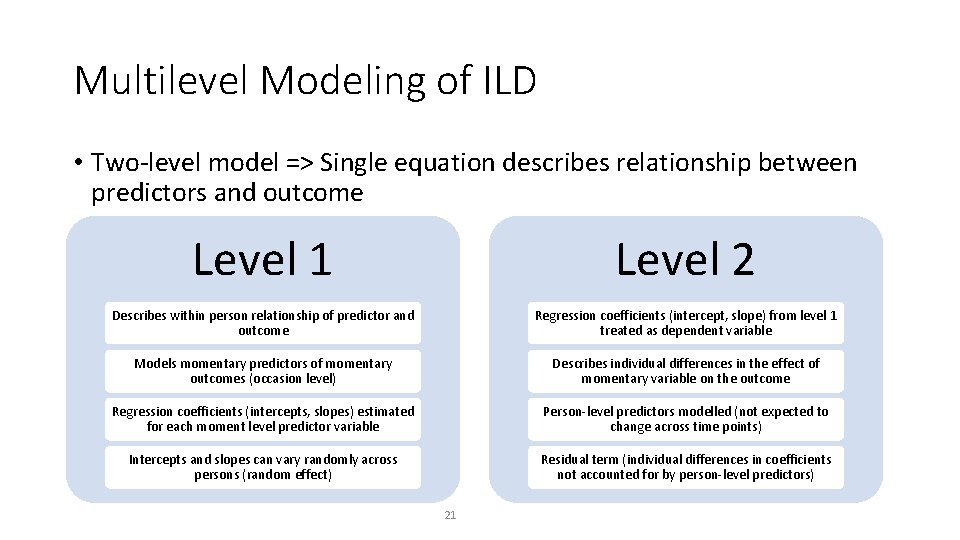
Mixed / Multilevel Modeling of ILD • Why use multilevel modeling? • Correctly accounts for clustering in data • Model fixed or random effects • Fixed – assume effect of predictor on outcome constant across people • Random – allows effect of predictor on outcome to vary across people • Robust to missing data • Participants do not need same number or timing of observations 13

Research Question 1: Model • Research question • Are changes in a person’s urge (yit) related to receiving a message tailored to reduce the urge to smoke in the previous assessment (zit)? • • Level 1 equation: • yit = π0 i + π1 i zit + εit • Level 2 equations: • π0 i = β 00 + δ 0 i and • Combined equation: • π1 i = β 10 • • yit = β 00 + β 10 zit + δ 0 i + εit • 14 i and t index assessment and subject yit is the outcome on assessment i for subject t zit is the momentary predictor on assessment i for subject t π0 i = β 00 + δ 0 i represents a random effect for intercept π1 i = β 10 represents a fixed effect for slope β 00 intercept δ 0 i portion of y not explained by person-level predictors εit portion of y not explained by momentary predictors

Research Question 1: Model • Research question • Are changes in a person’s urge (yit) related to receiving a message tailored to reduce the urge to smoke in the previous assessment (zit)? • • Level 1 equation: • yit = π0 i + π1 i zit + εit • Level 2 equations: • π0 i = β 00 + δ 0 i and • Combined equation: • π1 i = β 10 • • yit = β 00 + β 10 zit + δ 0 i + εit • 15 i and t index assessment and subject yit is the outcome on assessment i for subject t zit is the momentary predictor on assessment i for subject t π0 i = β 00 + δ 0 i represents a random effect for intercept π1 i = β 10 represents a fixed effect for slope β 00 intercept δ 0 i portion of y not explained by person-level predictors εit portion of y not explained by momentary predictors

Research Question 1: Results • Fixed effects • Tailored urge messages correspond to greater reductions in the urge at next assessment compared with untailored messages • -0. 29 (95% CI: -0. 43, -0. 15) • Random effects • Level 2 • Intercept = 0. 2 (95% CI: 0. 09, 0. 79) • Level 1 • Residual = 0. 43 (95% CI: 0. 39, 0. 49) • Autocorrelation = 0. 16 (95% CI: 0. 14, 0. 18) 16

Research Question 2: Model • Research question • Does the relationship between self-efficacy today (yit) and smoking cigarettes in the previous day (zit) vary across individuals? • • Level 1 equation: • yit = π0 i + π1 i zit + εit • Level 2 equations: • π0 i = β 00 + δ 0 i and • Combined equation: • π1 i = β 10 + δ 1 i • yit = β 00 + β 10 zit + δ 0 i + εit • • 17 i and t index assessment and subject yit is the outcome on assessment i for subject t zit is the momentary predictor on assessment i for subject t π0 i = β 00 + δ 0 i represents a random effect for intercept π1 i = β 10 + δ 1 i represents a fixed effect for slope β 00 intercept δ 0 i portion of y not explained by person-level predictors εit portion of y not explained by momentary predictors

Research Question 2: Results • Fixed effects • Smoking the day before corresponds with greater reduction in selfefficacy score the next day compared with not smoking • -0. 14 (95% CI: -0. 19, -0. 08) • Random effects • Level 2 • Intercept = 0. 45 (95% CI: 0. 29, 0. 77) • Smoking = 0. 02 (95% CI: 0. 008, 0. 05) • Intercept and smoking = -0. 03 (95% CI: -0. 07, 0. 009) • Level 1 • Residual = 0. 38 (95% CI: 0. 34, 0. 42) • Autocorrelation = 0. 28 (95% CI: 0. 21, 0. 34) 18

Multilevel Modeling and Beyond • Goals of ILD studies • Estimation of relationships that change over time both among individuals and within them • Estimate impact of predictor on outcome • Actual value or change in value • Synchronous or sequential • Estimate associations with cyclic or periodic patterns • Estimate variability or volatility • Identify differences based on person-level baseline predictors • Identify difference before versus after an event 19

Acknowledgements Co-Authors • Michael Businelle, Ph. D • Darla Kendzor, Ph. D • Emily Hébert, Dr. Ph Funding • American Cancer Society (PI: Businelle; MRSGT-12 -114 -01 -CPPB) • Oklahoma Tobacco Settlement Endowment Trust (092 -016 -0002 l) • University of Oklahoma Health Sciences Center • Stephenson Cancer Center • Oklahoma Tobacco Research Center 20

Multilevel Modeling of ILD • Two-level model => Single equation describes relationship between predictors and outcome Level 1 Level 2 Describes within person relationship of predictor and outcome Regression coefficients (intercept, slope) from level 1 treated as dependent variable Models momentary predictors of momentary outcomes (occasion level) Describes individual differences in the effect of momentary variable on the outcome Regression coefficients (intercepts, slopes) estimated for each moment level predictor variable Person-level predictors modelled (not expected to change across time points) Intercepts and slopes can vary randomly across persons (random effect) Residual term (individual differences in coefficients not accounted for by person-level predictors) 21

JITAI Example – Physical Activity • Decision Point: Specific time of the day • Decision Rule: If participant has been sedentary for 90 minutes, recommend exercise. • Tailoring Variables: Participant’s step count • Proximal Outcome: Daily step count • Distal Outcome: Total physical activity over the study period 22

JITAI Message Examples Condition Themes Example Messages Participant not interested in quitting • Benefits of quitting • General motivation • Planning for quit attempt On average, non-smokers live 12 years longer than smokers AND ex-smokers live up to 10 years longer than smokers who don’t quit. Low risk of imminent Lapse • General cessation advice • Maintaining abstinence Remember: Every day without cigarettes is a success. The first few hours and days are the hardest. It gets easier as time goes by. HANG IN THERE! You’re doing it! • Tailored to highest risk factor (e. g. , urge, stress) Don’t let negative emotions keep you from a healthier life! When you feel stressed or angry, distract yourself, go for a walk, get out of the situation for a few minutes, try deep breathing exercises. High risk of imminent Lapse 23

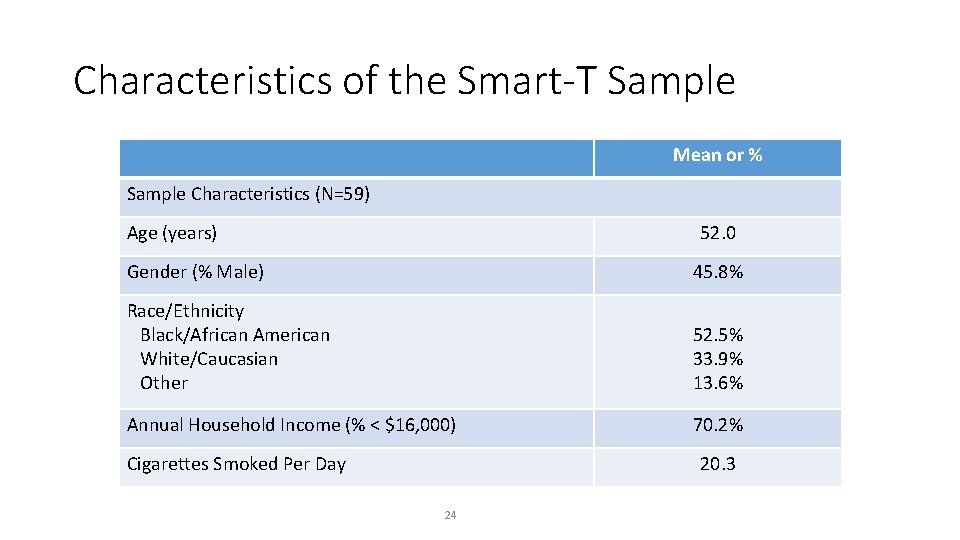
Characteristics of the Smart-T Sample Mean or % Sample Characteristics (N=59) Age (years) 52. 0 Gender (% Male) 45. 8% Race/Ethnicity Black/African American White/Caucasian Other 52. 5% 33. 9% 13. 6% Annual Household Income (% < $16, 000) 70. 2% Cigarettes Smoked Per Day 20. 3 24

Project Smart-T EMA data EMA Variables (N=59) Random EMAs Completed 3, 762 observations (85%) Daily Diary 1, 194 observations (92%) Self Initiated Assessments (smoking, urge, lapse) Total Observations (per participant) 1, 069 observations 6025 (102. 1) Completion Rate 86. 6% # Phones Lost or Stolen 0 25

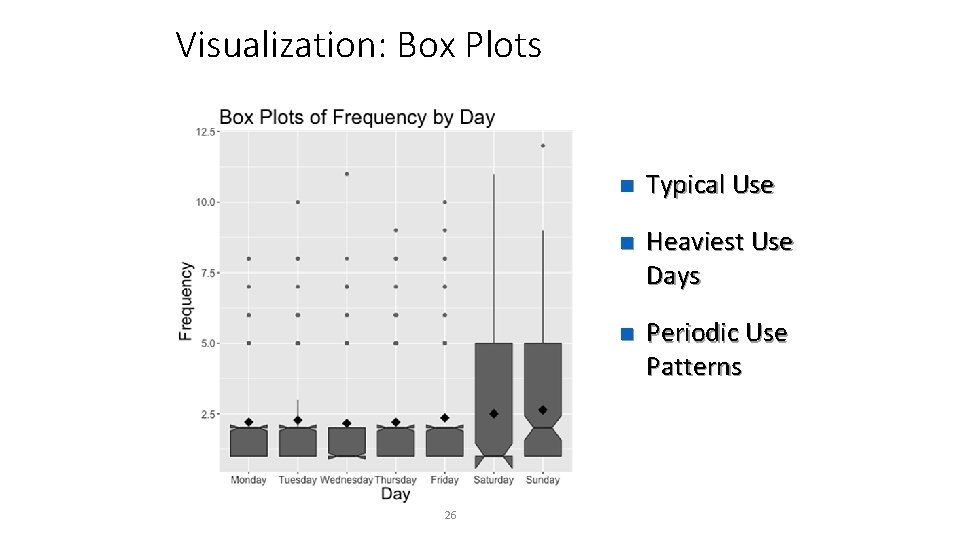
Visualization: Box Plots 26 n Typical Use n Heaviest Use Days n Periodic Use Patterns

Missingness in ILD • Can be due to the usual suspects • Loss to follow up • Sporadic missing • MCAR, MAR, or NMAR • Can be due to technology specific issues • Phone • Cell tower • Server Communication across technologies • Develop a plan for dealing with both in staff procedures and in analyses 27

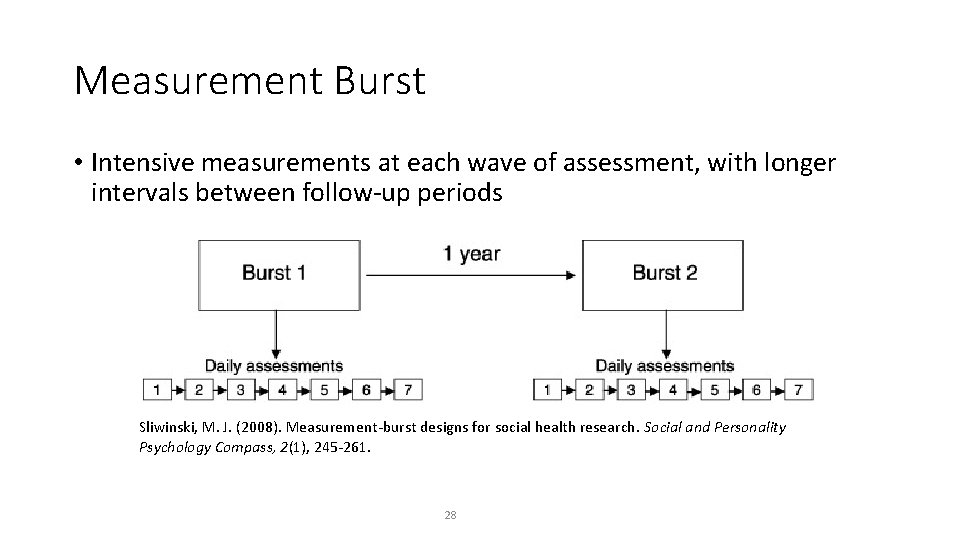
Measurement Burst • Intensive measurements at each wave of assessment, with longer intervals between follow-up periods Sliwinski, M. J. (2008). Measurement-burst designs for social health research. Social and Personality Psychology Compass, 2(1), 245 -261. 28