Introduction to Integer Programming l Integer programming models

Introduction to Integer Programming l Integer programming models 1 MIT and James Orlin © 2003

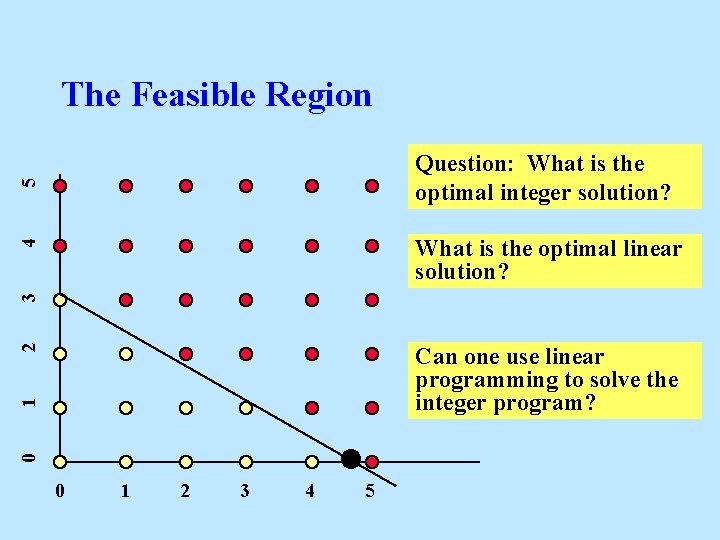
A 2 -Variable Integer program maximize 3 x + 4 y subject to 5 x + 8 y 24 x, y 0 and integer l What is the optimal solution? 2 MIT and James Orlin © 2003

The Feasible Region 5 Question: What is the optimal integer solution? 3 4 What is the optimal linear solution? 0 1 2 Can one use linear programming to solve the integer program? 0 1 2 3 4 5

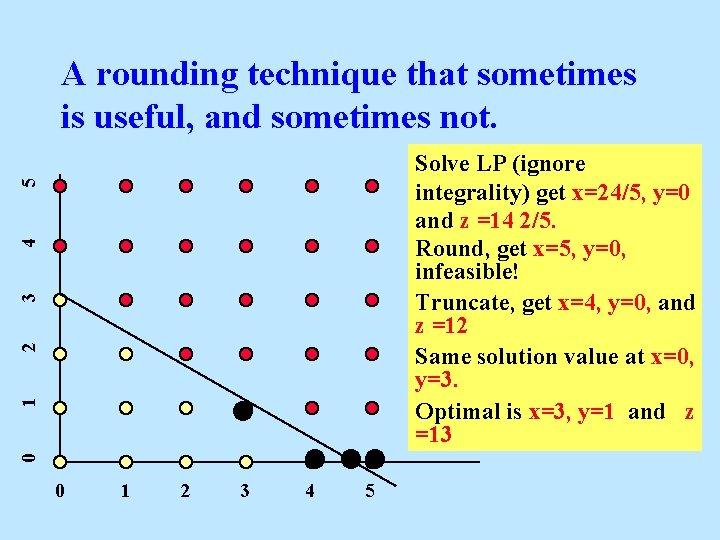
A rounding technique that sometimes is useful, and sometimes not. 0 1 2 3 4 5 Solve LP (ignore integrality) get x=24/5, y=0 and z =14 2/5. Round, get x=5, y=0, infeasible! Truncate, get x=4, y=0, and z =12 Same solution value at x=0, y=3. Optimal is x=3, y=1, and z =13 0 1 2 3 4 5

Why integer programs? l Advantages of restricting variables to take on integer values – More realistic – More flexibility l Disadvantages – More difficult to model – Can be much more difficult to solve 5 MIT and James Orlin © 2003

On 0 -1 variables l Integer programs: linear equalities and inequalities plus constraints that say a variable must be integer valued. l We also permit “xj {0, 1}. ” This is equivalent to 0 xj 1 and xj integer. 6 MIT and James Orlin © 2003

The mystery of integer programming Some integer programs are easy (we can solve problems with millions of variables) l Some integer programs are hard (even 100 variables can be challenging) l It takes expertise and experience to know which is which l It’s an active area of research at MIT and elsewhere l 7 MIT and James Orlin © 2003

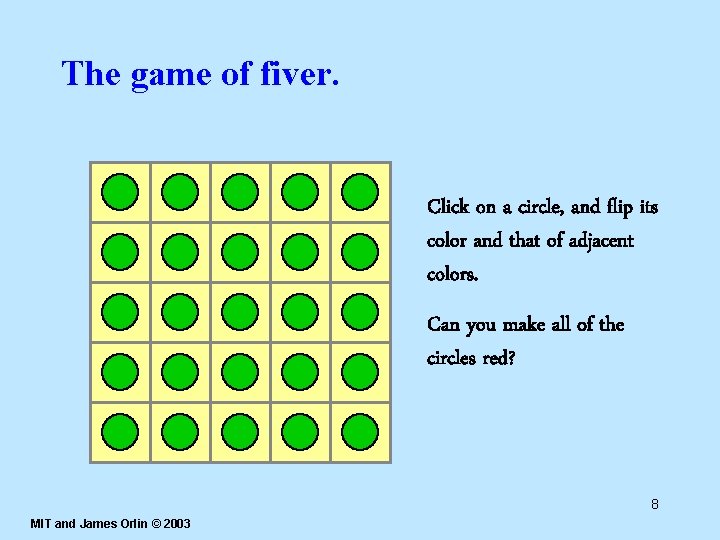
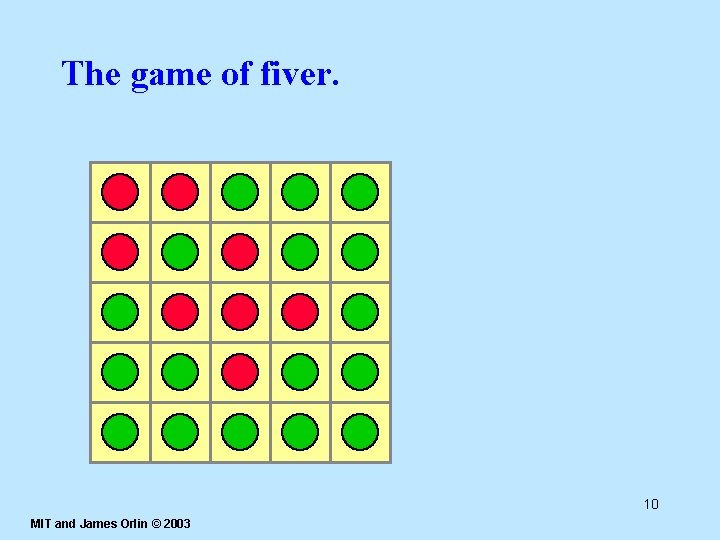
The game of fiver. Click on a circle, and flip its color and that of adjacent colors. Can you make all of the circles red? 8 MIT and James Orlin © 2003

The game of fiver. 9 MIT and James Orlin © 2003

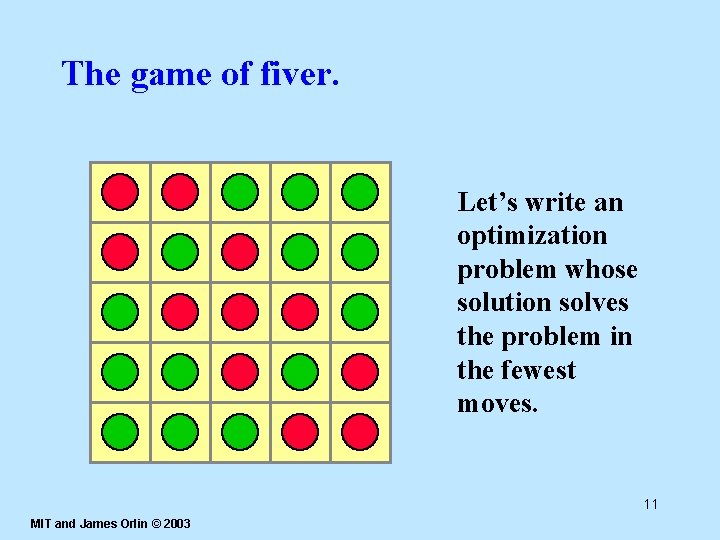
The game of fiver. 10 MIT and James Orlin © 2003

The game of fiver. Let’s write an optimization problem whose solution solves the problem in the fewest moves. 11 MIT and James Orlin © 2003

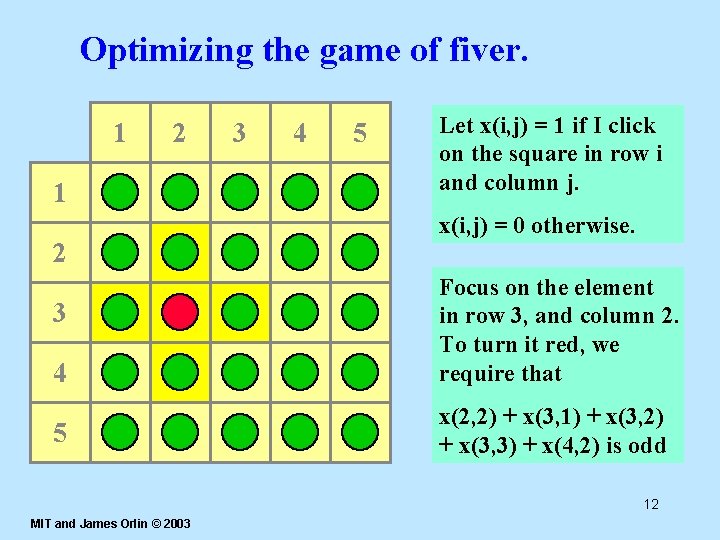
Optimizing the game of fiver. 1 2 3 4 5 Let x(i, j) = 1 if I click on the square in row i and column j. x(i, j) = 0 otherwise. 4 Focus on the element in row 3, and column 2. To turn it red, we require that 5 x(2, 2) + x(3, 1) + x(3, 2) + x(3, 3) + x(4, 2) is odd 3 12 MIT and James Orlin © 2003

Optimizing the game of fiver (i, j) to be red for i = 1 to 5 and for j = 1 to 5 l We want to minimize the number of moves. l Minimize S i, j=1 to 5 x(i, j) Subject to x(i, j) + x(i, j-1) + x(i, j+1) + x(i-1, j) + x(i+1, j) is odd for i = 1 to 5, j = 1 to 5 x(i, j) is 0 or 1 for i = 1 to 5 and j = 1 to 5 x(i, j) = 0 otherwise. l This (with a little modification) is an integer program. 13 MIT and James Orlin © 2003

Optimizing the game of fiver (i, j) to be red for i = 1 to 5 and for j = 1 to 5 l We want to minimize the number of moves. l Minimize S i, j=1 to 5 x(i, j) Subject to x(i, j) + x(i, j-1) + x(i, j+1) + x(i-1, j) + x(i+1, j) - 2 y(i, j) = 1 for i = 1 to 5, j = 1 to 5 x(i, j) is 0 or 1 for i = 1 to 5 and j = 1 to 5 y(i, j) is integral x(i, j) = 0 otherwise. l This is an integer program. MIT and James Orlin © 2003 14

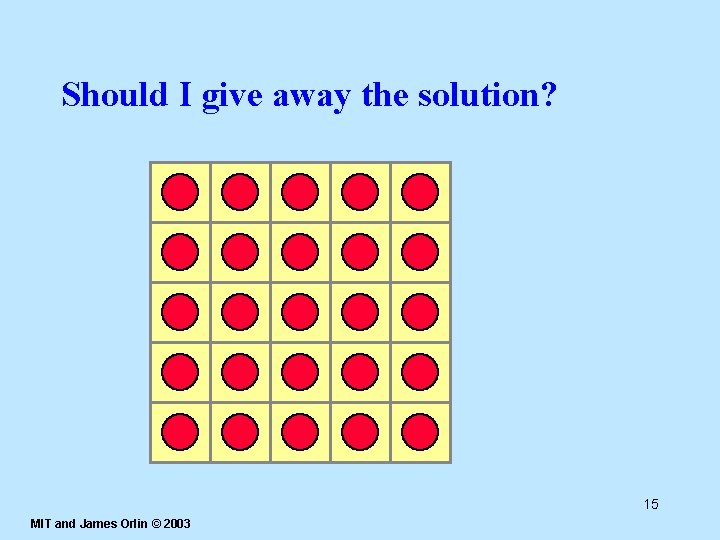
Should I give away the solution? 15 MIT and James Orlin © 2003

Types of integer programs l All integer programs have linear equalities and inequalities and some or all of the variables are required to be integer. – If all variables are required to be integer, then it is usually called a pure integer program. – If all variables are required to be 0 or 1, it is called a binary integer program, or a 0 -1 integer program. – if some variables can be fractional and others are required to be integers, it is called a mixed linear integer program (MILP) 16 MIT and James Orlin © 2003

Stockco Example Stockco is considering 6 investments. The cash required from each investment as well as the NPV of the investment is given next. The cash available for the investments is $14, 000. Stockco wants to maximize its NPV. What is the optimal strategy? An investment can be selected or not. One cannot select a fraction of an investment. 17 MIT and James Orlin © 2003

Data for the Stockco Problem Investment budget = $14, 000 18 MIT and James Orlin © 2003

Integer Programming Formulation What are the decision variables? Objective and Constraints? Max 16 x 1+ 22 x 2+ 12 x 3+ 8 x 4+ 11 x 5+ 19 x 6 5 x 1+ 7 x 2+ 4 x 3+ 3 x 4+ 4 x 5+ 6 x 6 14 MIT and James Orlin © 2003 xj e {0, 1} for each j = 1 to 6 19

Possible constraints in integer programs The previous constraints represent “economic indivisibilities”, either a project is selected, or it is not. There is no selecting of a fraction of a project. l Similarly, integer variables can model logical requirements (e. g. , if stock 2 is selected, then so is stock 1. ) l 20 MIT and James Orlin © 2003

How to model “logical” constraints Exactly 3 stocks are selected. l If stock 2 is selected, then so is stock 1. l If stock 1 is selected, then stock 3 is not selected. l Either stock 4 is selected or stock 5 is selected, but not both. l 21 MIT and James Orlin © 2003

Formulating Constraints l Exactly 3 stocks are selected x 1+ x 2+ x 3+ x 4+ x 5+ x 6=3 22 MIT and James Orlin © 2003

If stock 2 is selected then so is stock 1 A 2 -dimensional representation The integer programming constraint: x 1 x 2 Stock 1 MIT and James Orlin © 2003 Work with your partner for 5 minutes trying to model the other constraints. 23

If stock 1 is selected then stock 3 is not selected A 2 -dimensional representation The integer programming constraint: x 1 + x 3 1 Stock 3 Stock 1 24 MIT and James Orlin © 2003

Either stock 4 is selected or stock 5 is selected, but not both. A 2 -dimensional representation The integer programming constraint: x 4 + x 5 = 1 stock 5 stock 4 25 MIT and James Orlin © 2003

Representing Non-linear functions l Suppose that the cost of computers is as follows: – – $2, 000 each if you buy 1 to 10 $1, 800 for each computer from 11 to 25 $1, 700 for each computer from 26 to 50 No more than 50 may be purchased. – – Let x = number of computers bought x 1 = number bought at $2, 000 x 2 = number bought at $1, 800 x 3 = number bought at $1, 700 s. t. 0 x 1 10 0 x 2 15 0 x 3 25 If x 1 < 10, then x 2 = 0. If x 2 < 15, then x 3 = 0. Minimize 2, 000 x 1 +1, 800 x 2 + 1, 700 x 3 26 MIT and James Orlin © 2003

Representing Non-linear functions Minimize 2, 000 x 1 +1, 800 x 2 + 1, 700 x 3 s. t. 0 x 1 10 0 x 2 15 w 1 Let w 1 = 1 if x 1 = 10 w 1 = 0 if x 1 < 10 0 x 3 25 w 2 If 0 x 1 w<1 10, x 1 then /10 x 2 = 0. If 0 x 2 w< 15, x then /15 x 3 = 0. 2 2 Let w 2 = 1 if x 2 = 15 w 2 = 0 if x 2 < 15 w 1, w 2 {0, 1} If x 1 < 10, then x 2 = 0. If w 1 = 0, then x 2 = 0. MIT and James Orlin © 2003 If x 2 < 15, then x 3 = 0. If w 2 = 0, then x 3 = 0. 27

Is this formulation correct? It models the x’s correctly. l It does not model the w’s perfectly. l – Suppose x 1 = 10, x 2 = x 3 = 0; – Then w 1 = 0 or 1 – Cost = 20, 000, regardless. 28 MIT and James Orlin © 2003

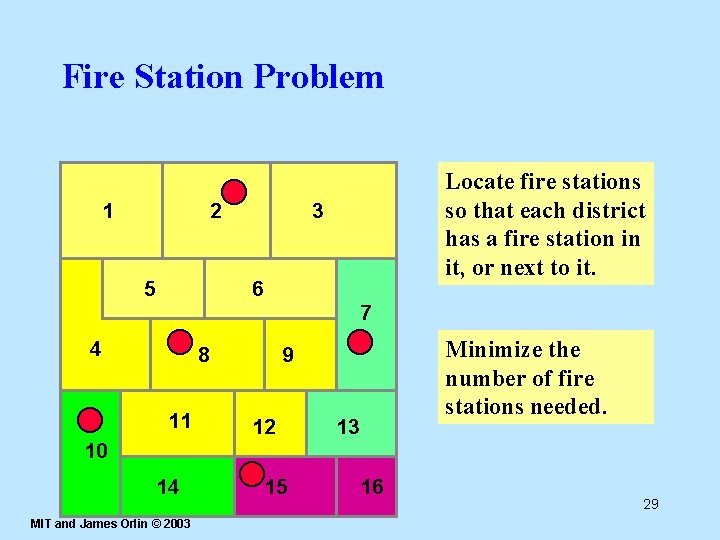
Fire Station Problem 1 2 5 Locate fire stations so that each district has a fire station in it, or next to it. 3 6 7 4 8 11 Minimize the number of fire stations needed. 9 12 13 10 14 MIT and James Orlin © 2003 15 16 29

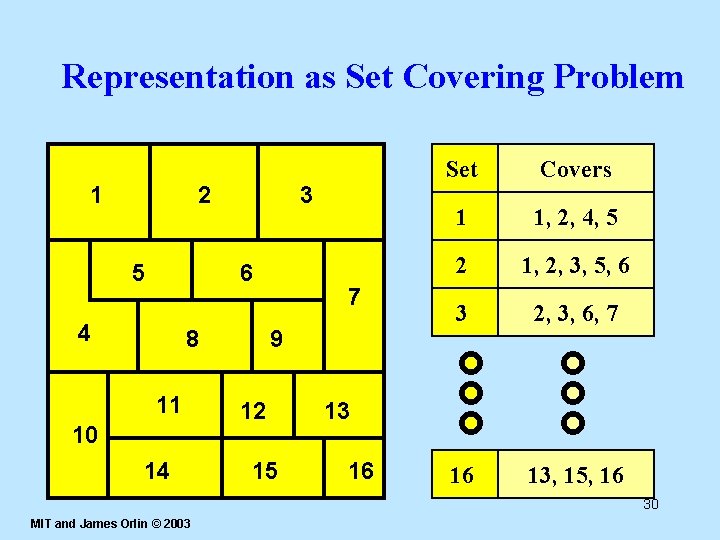
Representation as Set Covering Problem 1 2 5 3 6 4 8 11 10 14 7 9 12 15 Set Covers 1 1, 2, 4, 5 2 1, 2, 3, 5, 6 3 2, 3, 6, 7 16 13, 15, 16 13 16 30 MIT and James Orlin © 2003

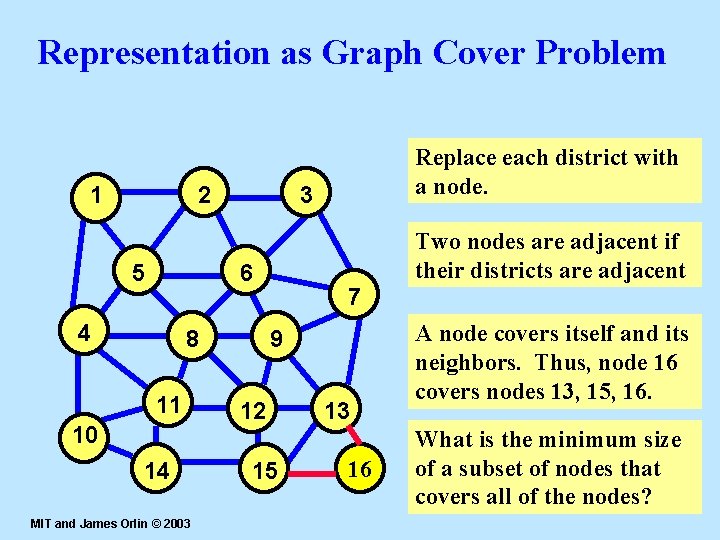
Representation as Graph Cover Problem 1 2 5 3 Two nodes are adjacent if their districts are adjacent 6 4 8 11 10 14 MIT and James Orlin © 2003 Replace each district with a node. 7 9 12 15 13 16 16 A node covers itself and its neighbors. Thus, node 16 covers nodes 13, 15, 16. What is the minimum size of a subset of nodes that covers all of the nodes? 31

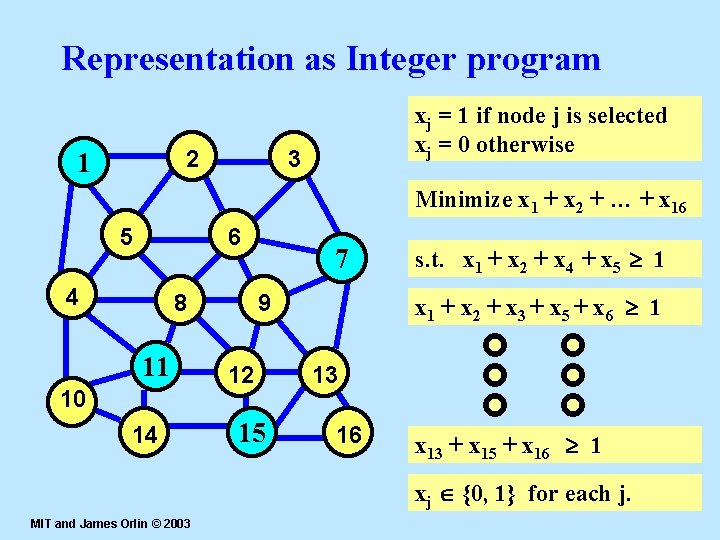
Representation as Integer program 11 2 xj = 1 if node j is selected xj = 0 otherwise 3 Minimize x 1 + x 2 + … + x 16 5 6 4 8 11 10 14 7 9 12 15 s. t. x 1 + x 2 + x 4 + x 5 1 x 1 + x 2 + x 3 + x 5 + x 6 1 13 16 x 13 + x 15 + x 16 1 xj {0, 1} for each j. MIT and James Orlin © 2003 32

skip Warehouse location problem l n warehouses – cost fj of opening warehouse j l m customers – customer i has a “demand” of di – unit shipping cost cij of serving customer i via warehouse j. l Variables: – let yj = 1 if warehouse j is opened – Let xij = amount of demand for customer i satisfied via warehouse j. 33 MIT and James Orlin © 2003

Suppose you knew which warehouses were open. S = set of open warehouses xij = demand satisfied for customer i at warehouse j l yj = 1 for j in S, yj = 0 for j not in S. l subject to: l customers get their demand satisfied l no shipments are made from an empty warehouse Si, j cijxij + Sj S fj minimize Sj xij = di xij = 0 if yj = 1 if yj = 0 and x 0 34 MIT and James Orlin © 2003

More on warehouse location yj = 1 if warehouse i is opened yj = 0 otherwise l xij = flow from i to j l Si, j cijxij + S j f i yi minimize subject to: customers get their demand satisfied l each warehouse is either opened or it is not (no partial openings) l no shipments are made from an empty warehouse l MIT and James Orlin © 2003 Si xij = dj 0 yj 1 yj integral for all j. xij dj yi for all i, j and x 0 35

Two key aspects of using integrality in the model l Costs: we include the cost of the warehouse only if it is opened. S i f i yi l Constraints: We do not allow shipping from warehouse j if it is not opened. – xij dj yi for all i, j 36 MIT and James Orlin © 2003

More on warehouse location l The above is a core subproblem occurring in supply chain management, and it can be enriched – – – – more complex distribution system capacity constraints non-linear transportation costs delivery times multiple products business rules and more 37 MIT and James Orlin © 2003

Using Excel Solver to Solve Integer Programs Add the integrality constraints (or add that a variable is binary) l Set the Solver Tolerance. (The tolerance is the percentage deviation from optimality allowed by solver in solving Integer Programs. ) – The default is 5% – The default is way to high – It often finds the optimum for small problems l 38 MIT and James Orlin © 2003

Some Comments on IP models l There are often multiple ways of modeling the same integer program. l Solvers for integer programs are extremely sensitive to the formulation. (not true for LPs) 39 MIT and James Orlin © 2003

Example constraint A: 2 x 1 + 2 x 2 + … + 2 x 50 51 l constraint B: x 1 + x 2 + … + x 50 25 l – assume that x is binary constraints C: x 1 y, x 2 y, …, x 50 y (where y is binary) l constraint D: x 1 + … + x 50 y l B dominates A, C dominates D It is not obvious why, until you see the algorithms. 40 MIT and James Orlin © 2003

Summary on Integer Programming l Dramatically improves the modeling capability – – Economic indivisibilities Logical constraints Modeling nonlinearities classical problems in capital budgeting and in supply chain management Not as easy to model l Not as easy to solve. l 41 MIT and James Orlin © 2003