Introduction to Information Security Lecture 5 Hash Functions

Introduction to Information Security Lecture 5: Hash Functions and MAC 2009. 7. Prof. Kwangjo Kim

Contents 1. Introduction - Hash Function vs. MAC 2. Hash Functions v Security Requirements v Finding collisions – birthday paradox v Dedicated hash functions v SHA-1 v Hash functions based on block ciphers 3. Message Authentication Code v HMAC v CBC-MAC 2

1. Hash Functions vs. MAC 3

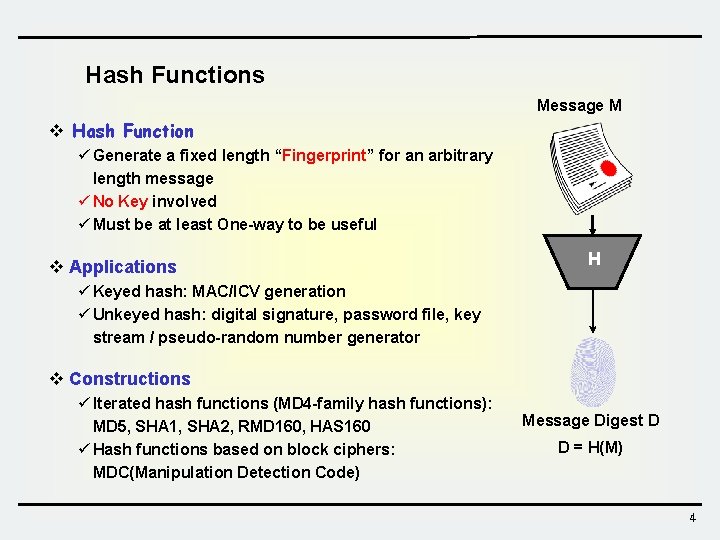
Hash Functions Message M v Hash Function ü Generate a fixed length “Fingerprint” for an arbitrary length message ü No Key involved ü Must be at least One-way to be useful v Applications H ü Keyed hash: MAC/ICV generation ü Unkeyed hash: digital signature, password file, key stream / pseudo-random number generator v Constructions ü Iterated hash functions (MD 4 -family hash functions): MD 5, SHA 1, SHA 2, RMD 160, HAS 160 ü Hash functions based on block ciphers: MDC(Manipulation Detection Code) Message Digest D D = H(M) 4

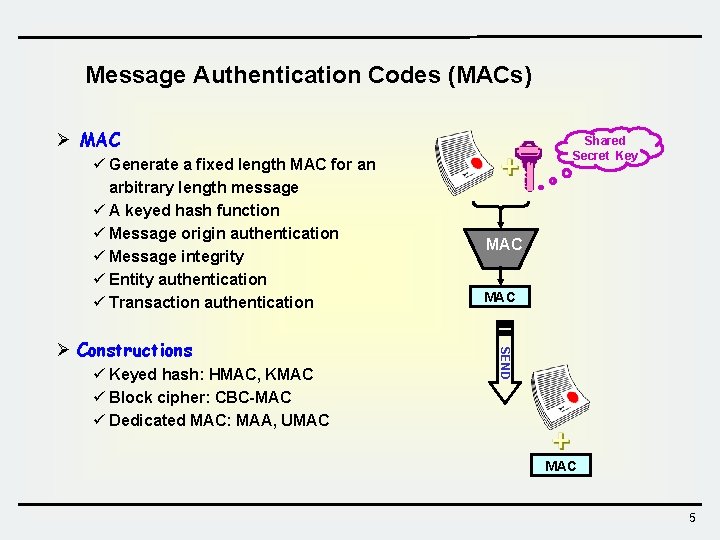
Message Authentication Codes (MACs) Ø MAC ü Generate a fixed length MAC for an arbitrary length message ü A keyed hash function ü Message origin authentication ü Message integrity ü Entity authentication ü Transaction authentication ü Keyed hash: HMAC, KMAC ü Block cipher: CBC-MAC ü Dedicated MAC: MAA, UMAC MAC SEND Ø Constructions Shared Secret Key MAC 5

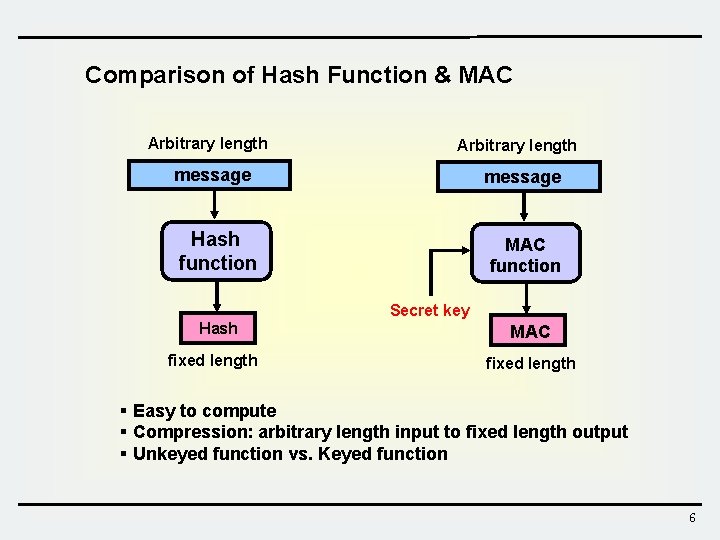
Comparison of Hash Function & MAC Arbitrary length message Hash function MAC function Secret key Hash fixed length MAC fixed length § Easy to compute § Compression: arbitrary length input to fixed length output § Unkeyed function vs. Keyed function 6

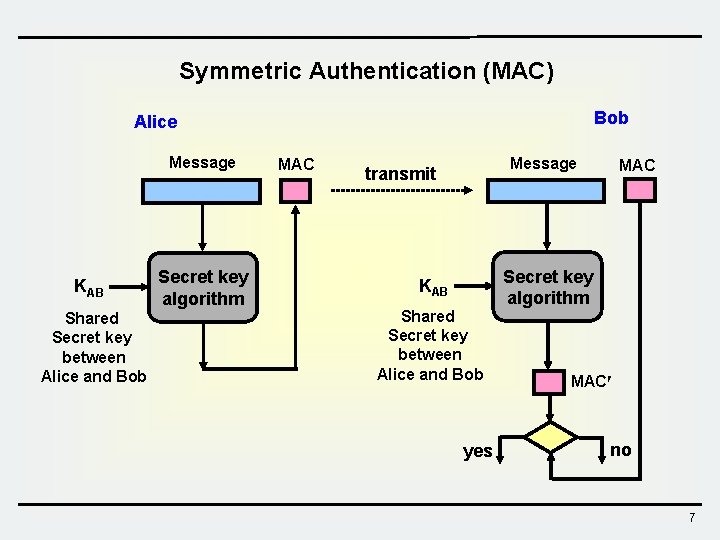
Symmetric Authentication (MAC) Bob Alice Message KAB Shared Secret key between Alice and Bob Secret key algorithm MAC Message transmit KAB Shared Secret key between Alice and Bob yes MAC Secret key algorithm MAC no 7

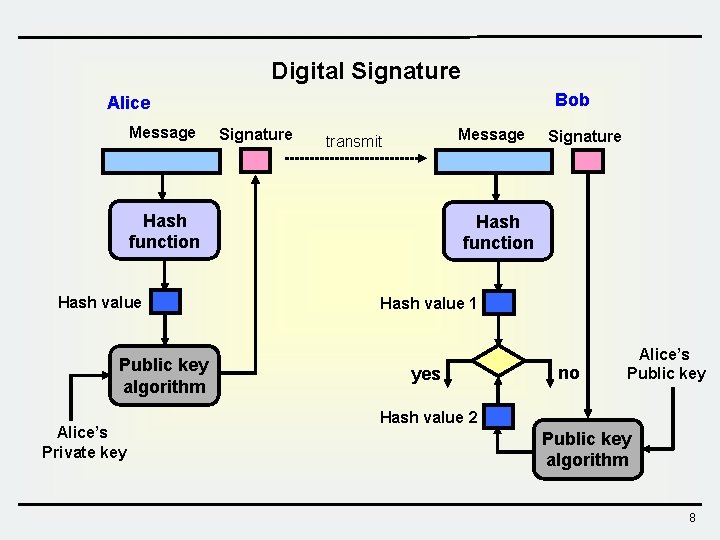
Digital Signature Bob Alice Message Signature Message transmit Hash function Hash value Public key algorithm Alice’s Private key Signature Hash function Hash value 1 yes no Alice’s Public key Hash value 2 Public key algorithm 8

MAC and Digital Signature v MAC (Message Authentication Code) Ø Generated and verified by a secret key algorithm Ø Message origin authentication & Message integrity Ø Schemes ü Keyed hash: HMAC ü Block cipher: CBC-MAC, XCBC-MAC ü Dedicated MAC: UMAC v Digital Signature Ø Generated and verified by a public key algorithm and a hash function Ø Message origin authentication & Message integrity Ø Non-repudiation Ø Schemes üHash + Digital signature algorithm üRSA; DSA, KCDSA; ECDSA, EC-KCDSA 9

2. Hash Functions 10

Hash Functions – Requirements v Definition Ø Compression: arbitrary length input to fixed length output Ø Ease of computation v Security Properties Ø Preimage resistance (One-wayness) : § Given y, it is computationally infeasible to find any input x such that y = h(x) Ø 2 nd preimage resistance (Weak collision resistance) : § Given x, it is computationally infeasible to find another input x x such that h(x) = h(x ) Ø Collision resistance (Strong collision resistance) : § It is computationally infeasible to find any two distinct inputs x and x such that h(x) = h(x ) 11

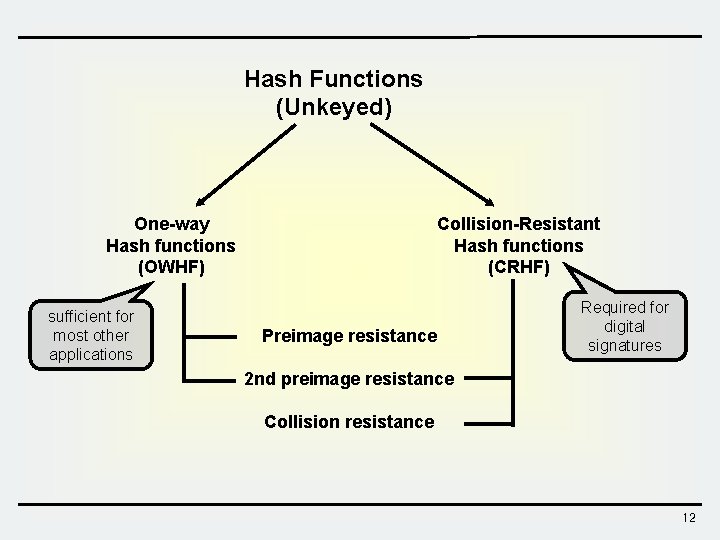
Hash Functions (Unkeyed) One-way Hash functions (OWHF) sufficient for most other applications Collision-Resistant Hash functions (CRHF) Preimage resistance Required for digital signatures 2 nd preimage resistance Collision resistance 12

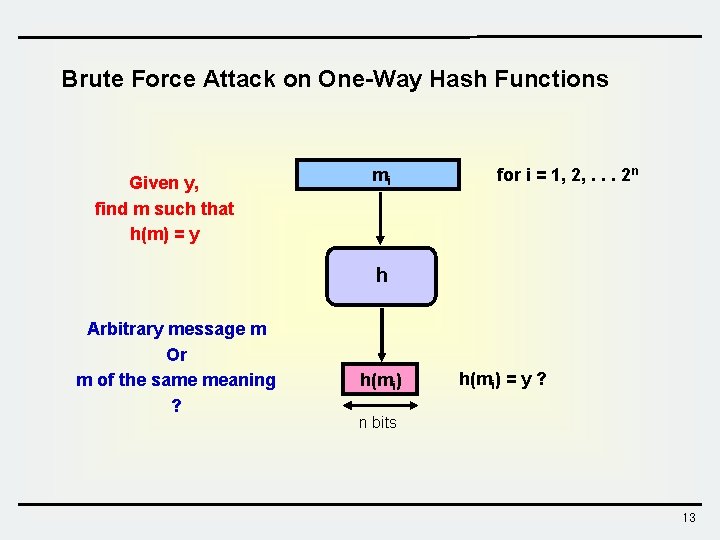
Brute Force Attack on One-Way Hash Functions Given y, find m such that h(m) = y mi for i = 1, 2, . . . 2 n h Arbitrary message m Or m of the same meaning ? h(mi) = y ? n bits 13

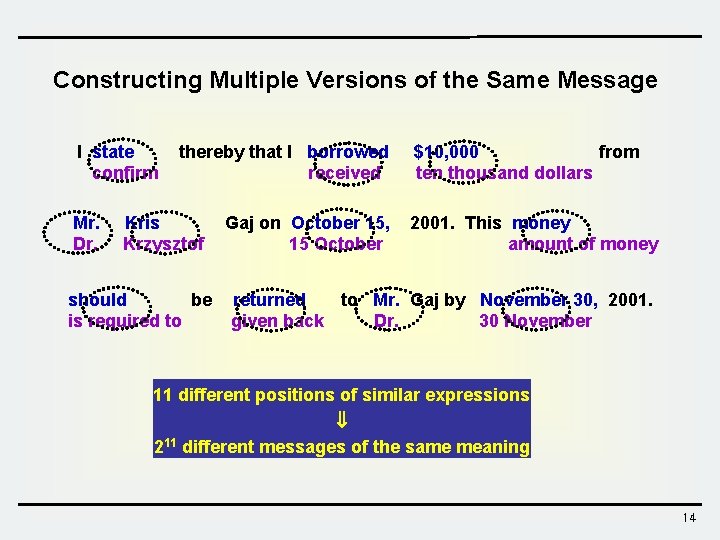
Constructing Multiple Versions of the Same Message I state confirm Mr. Dr. thereby that I borrowed received Kris Krzysztof should be is required to Gaj on October 15, 15 October $10, 000 from ten thousand dollars 2001. This money amount of money returned to Mr. Gaj by November 30, 2001. given back Dr. 30 November 11 different positions of similar expressions 211 different messages of the same meaning 14

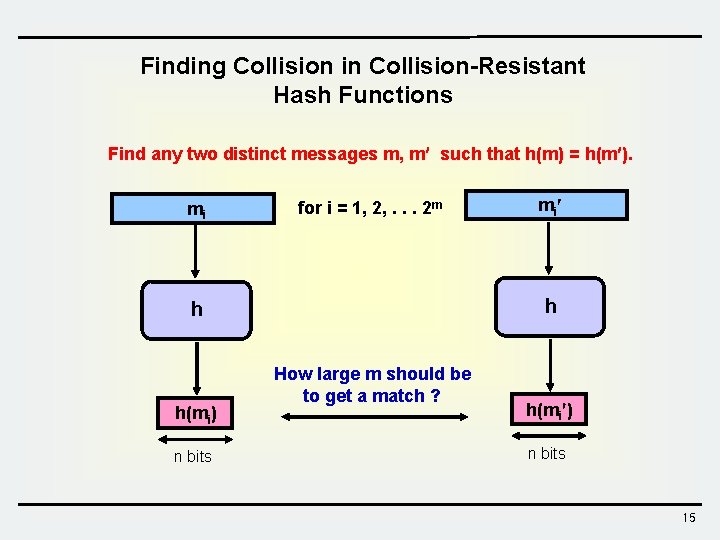
Finding Collision in Collision-Resistant Hash Functions Find any two distinct messages m, m such that h(m) = h(m ). mi for i = 1, 2, . . . 2 m h h h(mi) n bits mi How large m should be to get a match ? h(mi ) n bits 15

Birthday Paradox How many students there must be in a class for there be a greater than 50% chance that 1. One of the students shares the teacher’s birthday ? (complexity breaking one-wayness) 365/2 188 2. Any two of the students share the same birthday ? (complexity breaking collision resistance) 1 – 365 364 . . . (365 -k+1) / 365 k > 0. 5 k 23 In general, the probability of a match being found when k samples are randomly selected between 1 and n equals 16

Birthday Attack Consider two sets of k instances: X = {x 1, x 2, …, xk} ; Y = {y 1, y 2, …, yk}, The value of k making the probability of at least one match being greater than 0. 5 17

Birthday Attack on Collision Search H 1 H 2 H 3 . . . Hm Hm v Number of comparisons = m 2 v Suppose that digest size = n bits v Intuitively, Ø Hash values can take 2 n possible values Ø generate two sets of m=2 n/2 hash values Ø compare each element of the two sets Ø there is 2 n comparisons Ø probably there will be one match v More exactly, Ø 1. 66 x 2 n/2 hash values required to find a match with prob. >0. 5 18

One Million $ Hardware Brute Force Attack v One-Way Hash Functions (complexity = 2 n) Year 2001 n = 64 4 days n = 80 718 years n = 128 1017 years v Collision-Resistant Hash Functions (complexity = 2 n/2) Year 2001 n = 128 4 days n = 160 718 years n = 256 1017 years 19

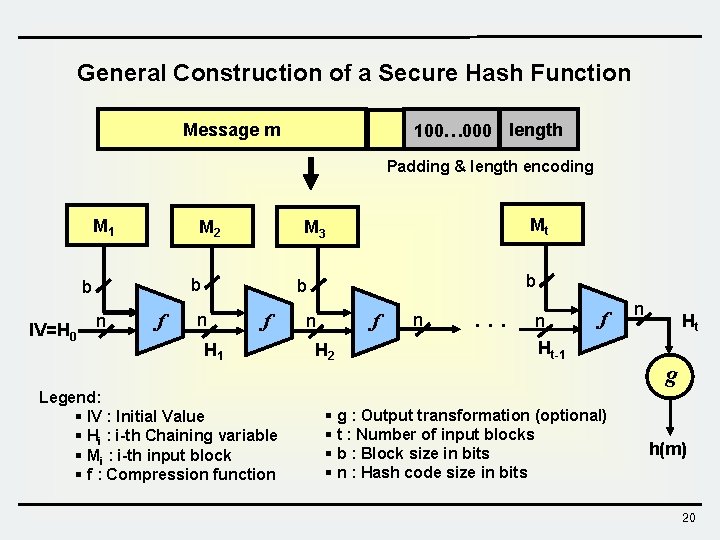
General Construction of a Secure Hash Function Message m 100… 000 length Padding & length encoding M 1 M 2 b b IV=H 0 n f Mt M 3 b b n f H 1 Legend: § IV : Initial Value § Hi : i-th Chaining variable § Mi : i-th input block § f : Compression function f n H 2 n . . . n f Ht-1 § g : Output transformation (optional) § t : Number of input blocks § b : Block size in bits § n : Hash code size in bits n Ht g h(m) 20

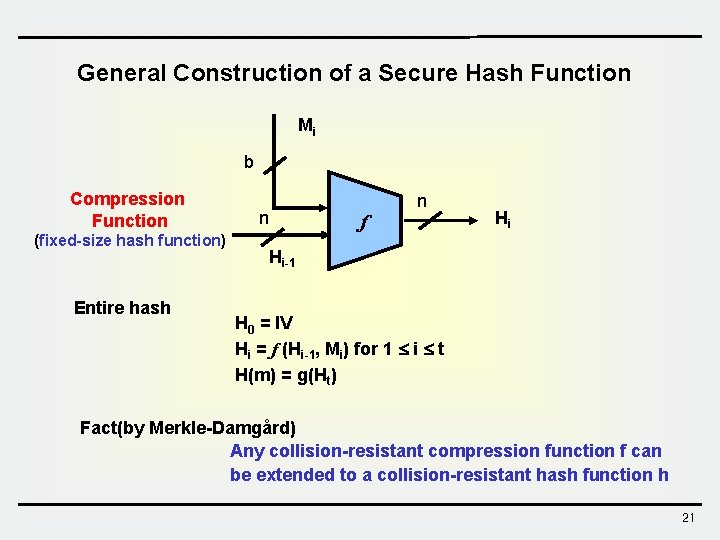
General Construction of a Secure Hash Function Mi b Compression Function (fixed-size hash function) Entire hash n f n Hi Hi-1 H 0 = IV Hi = f (Hi-1, Mi) for 1 i t H(m) = g(Ht) Fact(by Merkle-Damgård) Any collision-resistant compression function f can be extended to a collision-resistant hash function h 21

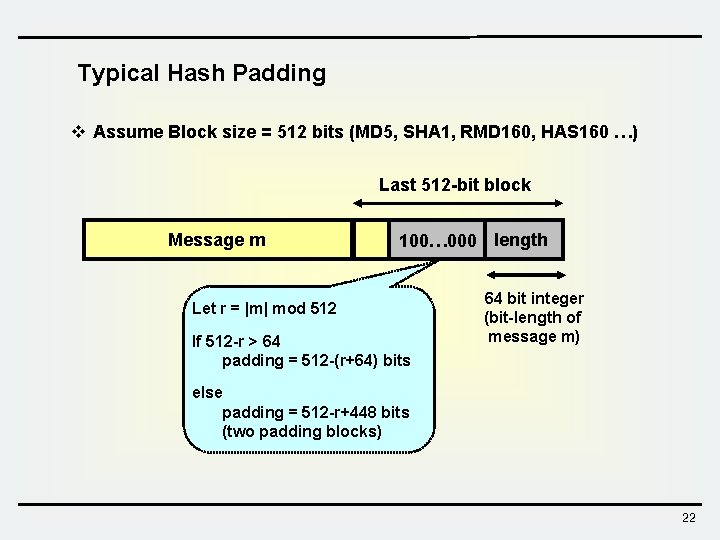
Typical Hash Padding v Assume Block size = 512 bits (MD 5, SHA 1, RMD 160, HAS 160 …) Last 512 -bit block Message m 100… 000 length Let r = |m| mod 512 If 512 -r > 64 padding = 512 -(r+64) bits 64 bit integer (bit-length of message m) else padding = 512 -r+448 bits (two padding blocks) 22

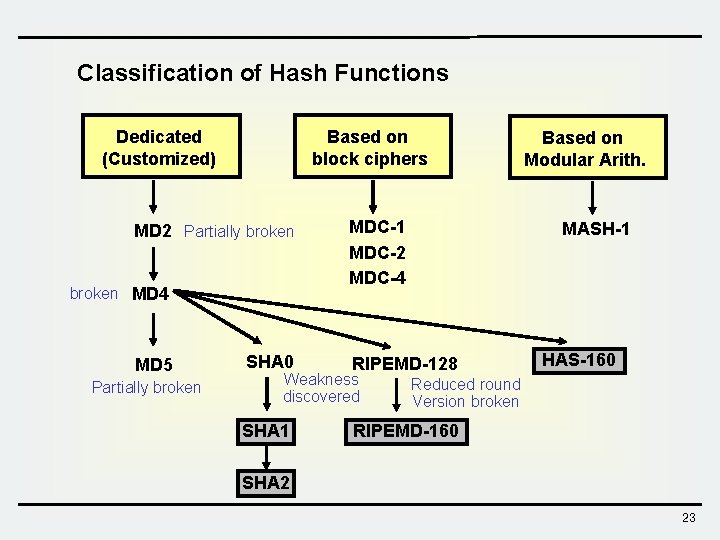
Classification of Hash Functions Dedicated (Customized) Based on block ciphers MD 2 Partially broken MD 4 MD 5 Partially broken SHA 0 MDC-1 MDC-2 MDC-4 SHA 1 MASH-1 RIPEMD-128 Weakness discovered Based on Modular Arith. HAS-160 Reduced round Version broken RIPEMD-160 SHA 2 23

SHA (Secure Hash Algorithm) v SHA was designed by NIST (national institute of standards and technology) & NSA (National Security Agency) in 1993, and revised as SHA-1 in 1995 * Federal Information Processing Standard v. SHA: FIPS PUB 180, 1993 v. SHA-1 : FIPS Pub 180 -1, 1995 v US standard for use with DSA signature scheme v The algorithm is SHA, the standard is SHS v Based on the design of MD 4 with key differences v SHA-1 : Secure Hash Standard (SHS), FIPS Pub 180 -1, 1995 v 160 -bit hash value (5 words Big Endian) v 512 -bit block size v 4 round hash, each round has 20 steps, total 80 steps 24

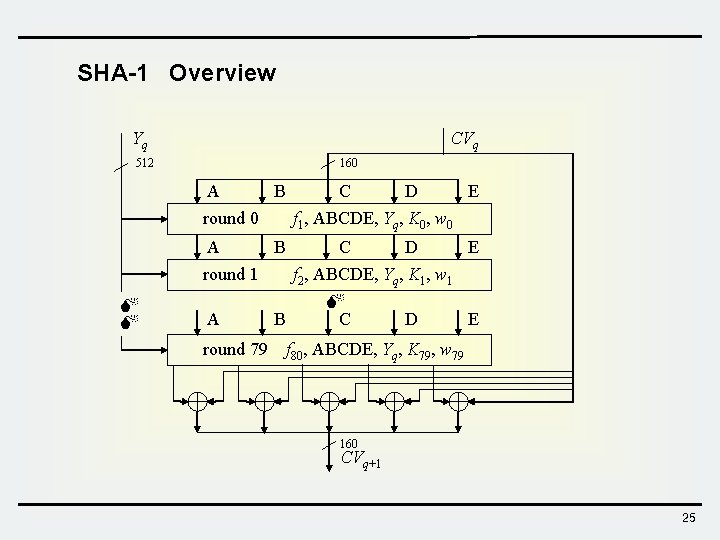
SHA-1 Overview Yq CVq 512 160 A B round 0 A A round 79 D E f 1, ABCDE, Yq, K 0, w 0 B round 1 C C D E f 2, ABCDE, Yq, K 1, w 1 B C D E f 80, ABCDE, Yq, K 79, w 79 160 CVq+1 25

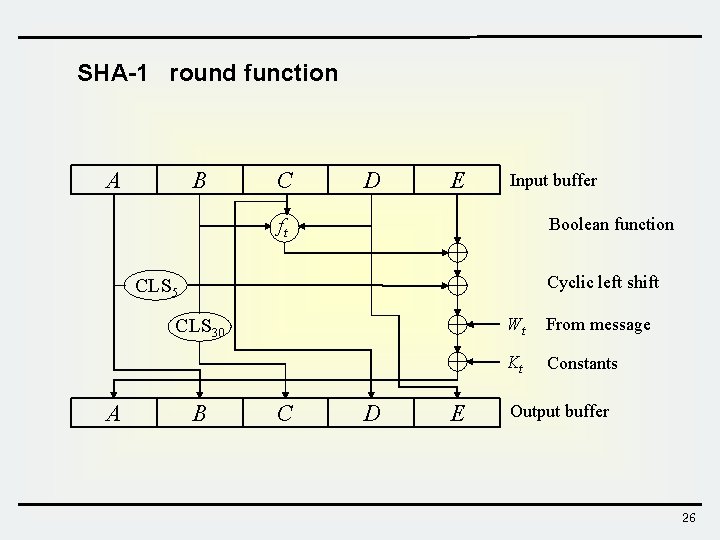
SHA-1 round function A B C D E Input buffer Boolean function ft Cyclic left shift CLS 5 CLS 30 A B C D E Wt From message Kt Constants Output buffer 26

SHA-1 Initial values A=67452301 B=EFCDAB 89 C=98 BADCFE D=10325476 E=C 3 D 2 E 1 F 0 Constants Kt t = 0 ~ 19 Kt = 5 A 8 2 7 9 9 9 t = 20 ~ 39 Kt = 6 E D 9 E B A 1 t = 40 ~ 59 Kt = 8 F 1 B B C D C t = 60 ~ 79 Kt = C A 6 2 C 1 D 6 Boolean function ft t = 0 ~ 19 t = 20 ~ 39 t = 40 ~ 59 t = 60 ~ 79 ft (B, C, D) = B · C + B · D ft (B, C, D) = B C D ft (B, C, D) = B · C + B · D + C · D ft (B, C, D) = B C D 27

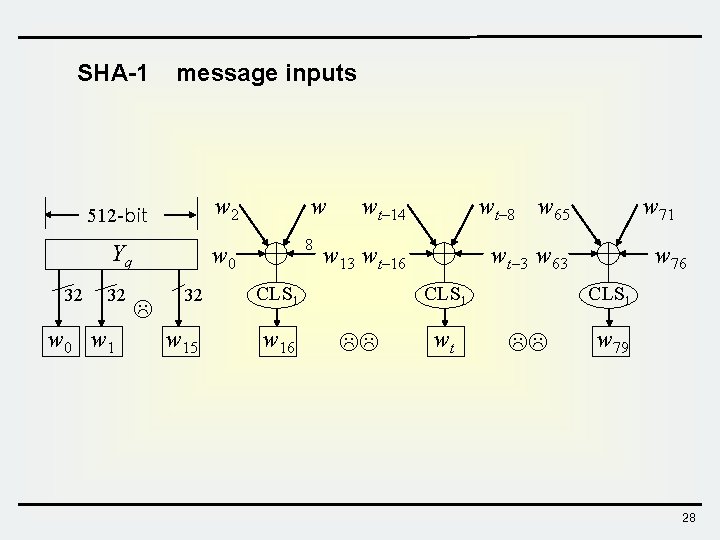
SHA-1 32 message inputs 512 -bit w 2 Yq w 0 32 w 0 w 1 w 8 32 CLS 1 w 15 w 16 wt– 14 wt– 8 w 65 w 13 wt– 16 wt– 3 w 63 CLS 1 wt w 71 w 76 CLS 1 w 79 28

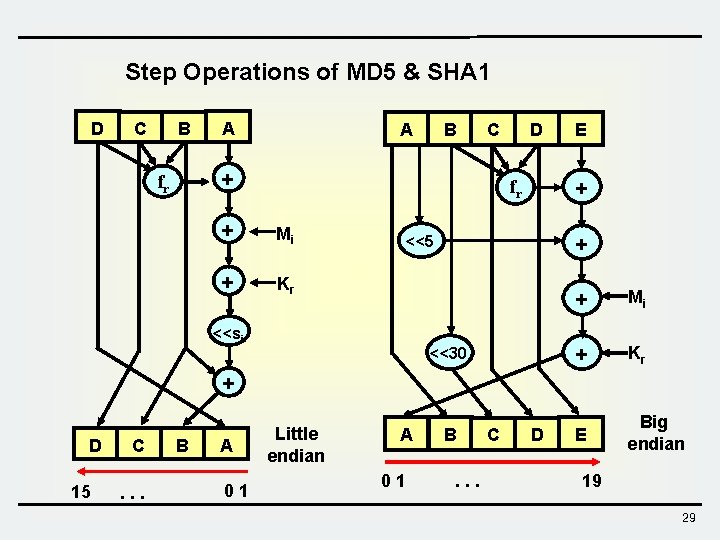
Step Operations of MD 5 & SHA 1 D C B A A B C + fr D + fr + Mi + Kr + <<5 <<si E <<30 + Mi + Kr E Big endian + D 15 C. . . B A 01 Little endian A 01 B. . . C D 19 29

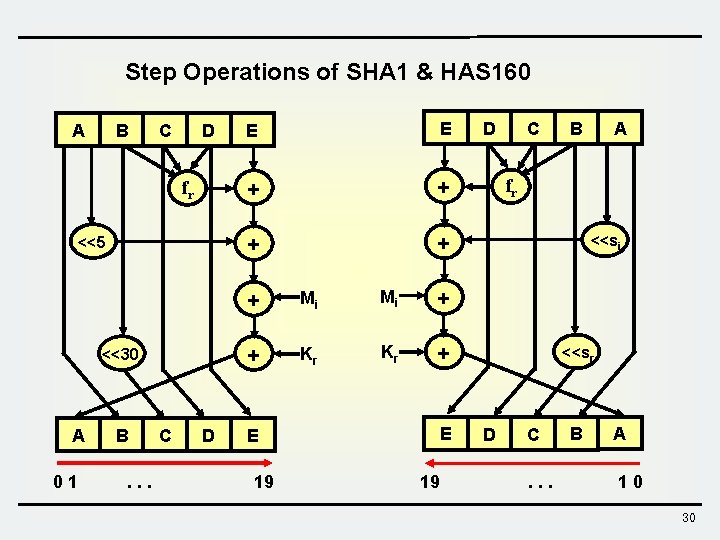
Step Operations of SHA 1 & HAS 160 A B C D fr <<5 <<30 A 01 B. . . C D E E + + + Mi Mi + + Kr Kr <<s +r E 19 D C A B fr <<si <<sr D C. . . B A 10 30

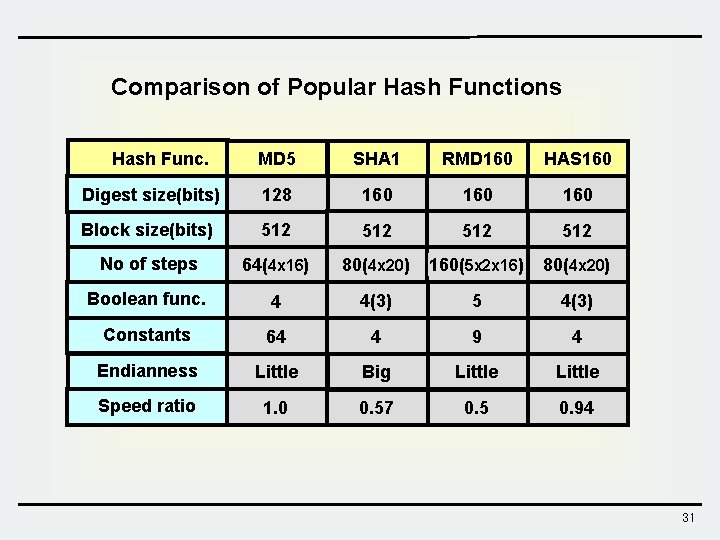
Comparison of Popular Hash Functions Hash Func. MD 5 SHA 1 RMD 160 HAS 160 Digest size(bits) 128 160 160 Block size(bits) 512 512 No of steps 64(4 x 16) 80(4 x 20) 160(5 x 2 x 16) 80(4 x 20) Boolean func. 4 4(3) 5 4(3) Constants 64 4 9 4 Endianness Little Big Little Speed ratio 1. 0 0. 57 0. 5 0. 94 31

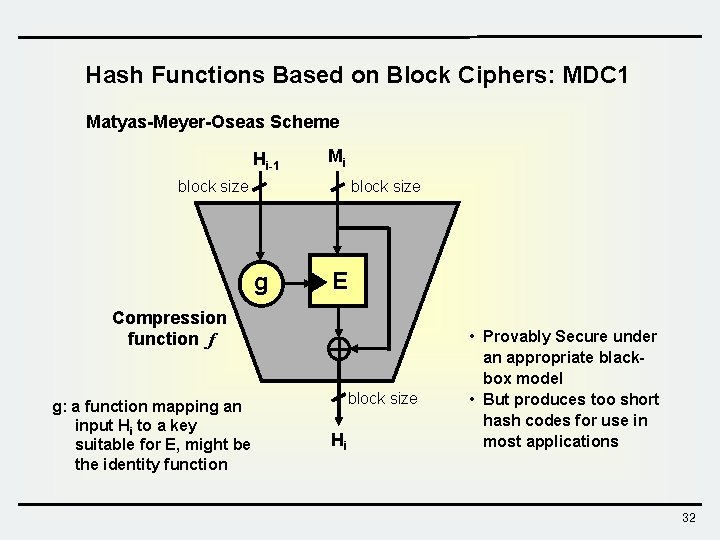
Hash Functions Based on Block Ciphers: MDC 1 Matyas-Meyer-Oseas Scheme Hi-1 Mi block size g E Compression function f g: a function mapping an input Hi to a key suitable for E, might be the identity function block size Hi • Provably Secure under an appropriate blackbox model • But produces too short hash codes for use in most applications 32

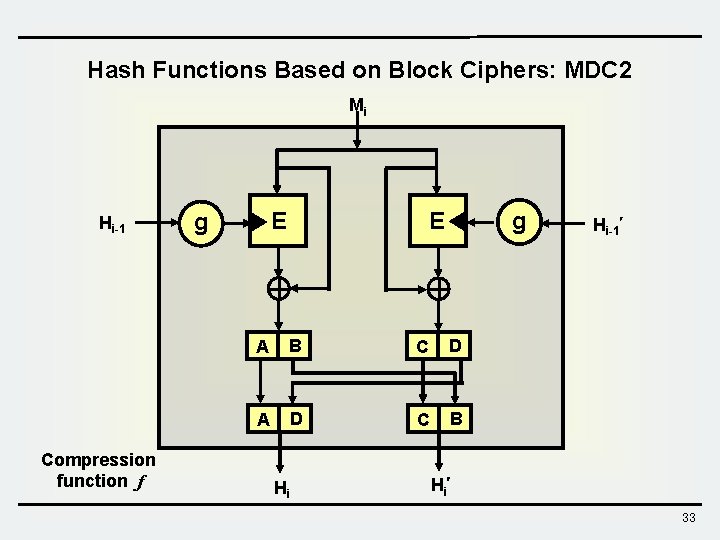
Hash Functions Based on Block Ciphers: MDC 2 Mi Hi-1 Compression function f E g g E A B C D A D C B Hi Hi-1 Hi 33

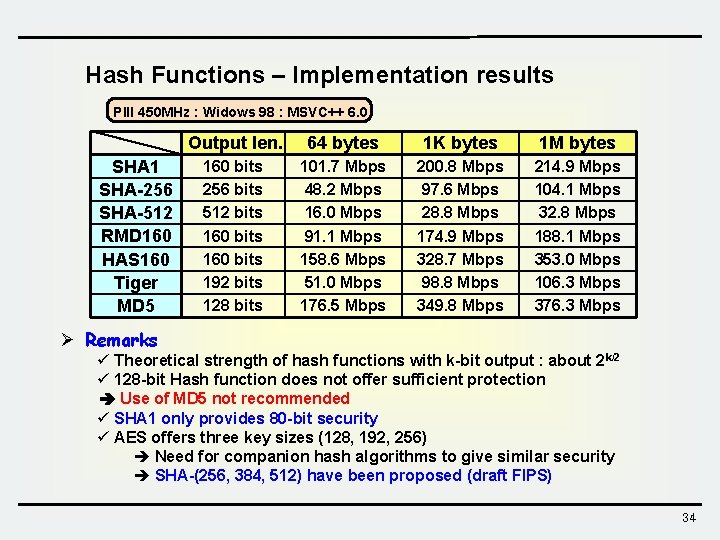
Hash Functions – Implementation results PIII 450 MHz : Widows 98 : MSVC++ 6. 0 SHA 1 SHA-256 SHA-512 RMD 160 HAS 160 Tiger MD 5 Output len. 64 bytes 1 K bytes 1 M bytes 160 bits 256 bits 512 bits 160 bits 192 bits 128 bits 101. 7 Mbps 48. 2 Mbps 16. 0 Mbps 91. 1 Mbps 158. 6 Mbps 51. 0 Mbps 176. 5 Mbps 200. 8 Mbps 97. 6 Mbps 28. 8 Mbps 174. 9 Mbps 328. 7 Mbps 98. 8 Mbps 349. 8 Mbps 214. 9 Mbps 104. 1 Mbps 32. 8 Mbps 188. 1 Mbps 353. 0 Mbps 106. 3 Mbps 376. 3 Mbps Ø Remarks ü Theoretical strength of hash functions with k-bit output : about 2 k/2 ü 128 -bit Hash function does not offer sufficient protection Use of MD 5 not recommended ü SHA 1 only provides 80 -bit security ü AES offers three key sizes (128, 192, 256) è Need for companion hash algorithms to give similar security è SHA-(256, 384, 512) have been proposed (draft FIPS) 34

3. Message Authentication Code 35

MAC Functions v MAC algorithms ØKeyed hash functions whose specific purpose is message authentication v Requirements ØEase of computation ØCompression arbitrary length input to fixed length output ØComputation resistance Given zero or more text-MAC pairs (mi, MACK(mi)), It’s computationally infeasible to find any new text-MAC pair (m, MACK(m)) for m mi 36

Attacks & Forgeries on MAC Algorithms v Adversary’s goal Ø MAC key recovery Ø MAC forgery v Attacks on MAC algorithms Ø Known-text attack Ø Chosen text attack Ø Adaptively chosen text attack v MAC Forgeries Ø Selective forgery Ø Existential forgery 37

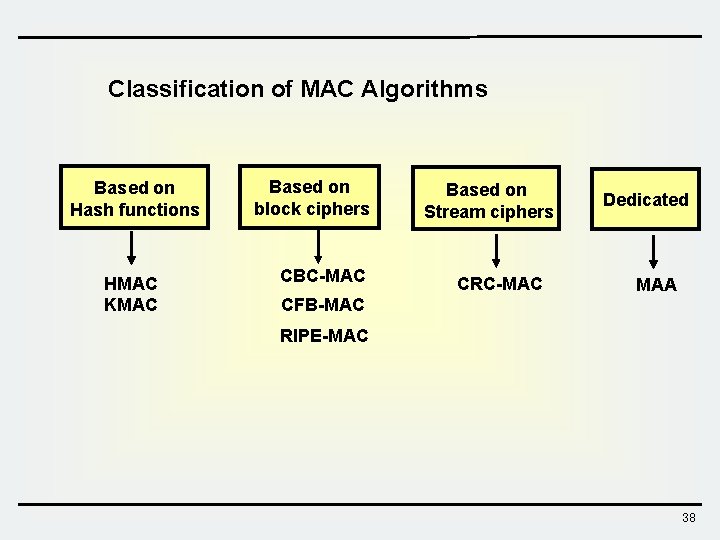
Classification of MAC Algorithms Based on Hash functions HMAC KMAC Based on block ciphers CBC-MAC Based on Stream ciphers CRC-MAC Dedicated MAA CFB-MAC RIPE-MAC 38

Constructing MAC from Hash Functions v Secret Prefix Method Ø MACK(M) = h(K || M) Ø Extension attack: easy to generate MAC for M = M || P || M (P: hash padding) v Secret Suffix Method Ø MACK(M) = h(M || K) Ø Birthday attack applies: if h(M) = h(M ), then MACK(M) = MACK(M ) v Envelope Method Ø MACK(M) = h(K || P || M || K) (P=padding to make K || P one block) Ø No known weakness yet v HMAC Ø Provably secure under some ideal assumptions on the underlying hash function http: //csrc. nist. gov/publications/fips 198/fips-198 a. pdf 39

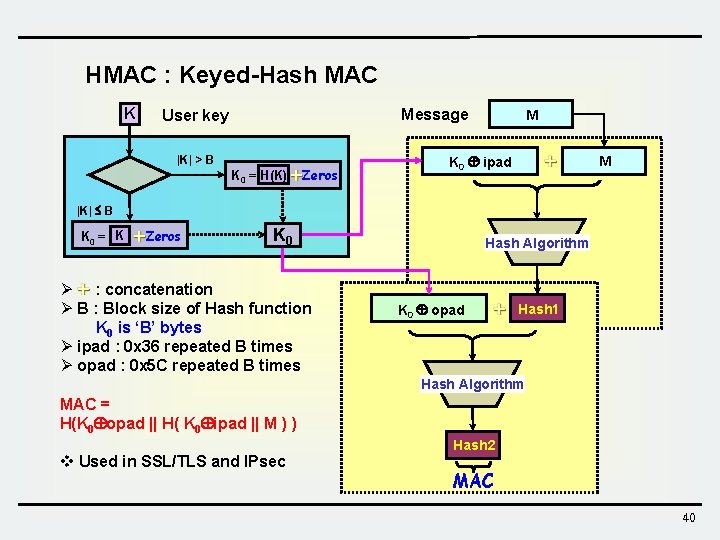
HMAC : Keyed-Hash MAC K Message User key |K| > B K 0 = H(K) Zeros M K 0 ipad M |K| B K 0 = K Zeros K 0 Ø : concatenation Ø B : Block size of Hash function K 0 is ‘B’ bytes Ø ipad : 0 x 36 repeated B times Ø opad : 0 x 5 C repeated B times Hash Algorithm K 0 opad Hash 1 Hash Algorithm MAC = H(K 0 opad || H( K 0 ipad || M ) ) v Used in SSL/TLS and IPsec Hash 2 MAC 40

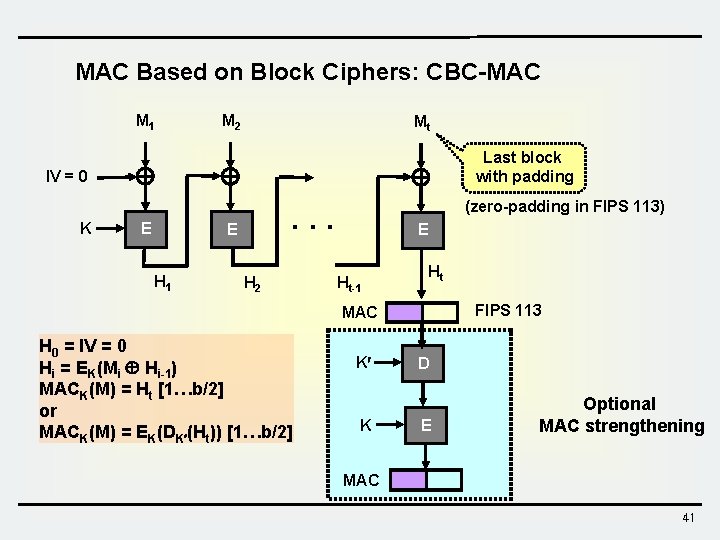
MAC Based on Block Ciphers: CBC-MAC M 1 M 2 Mt Last block with padding IV = 0 K E . . . E H 1 (zero-padding in FIPS 113) H 2 E Ht-1 Ht FIPS 113 MAC H 0 = IV = 0 Hi = EK(Mi Hi-1) MACK(M) = Ht [1…b/2] or MACK(M) = EK(DK (Ht)) [1…b/2] K K D E Optional MAC strengthening MAC 41

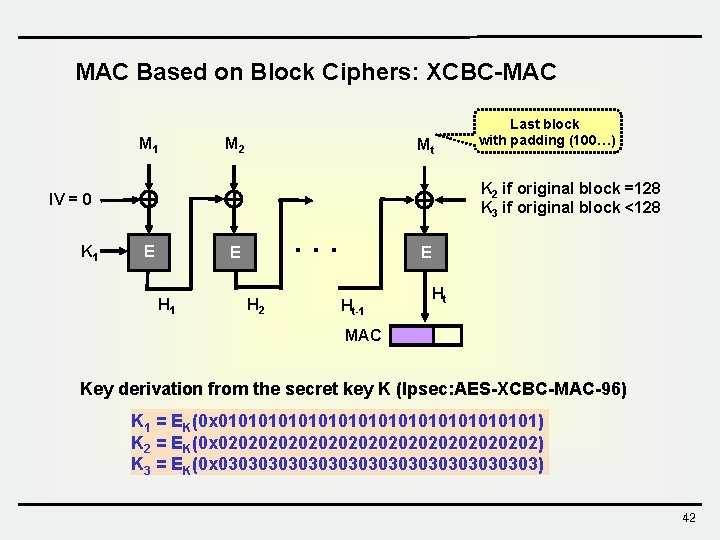
MAC Based on Block Ciphers: XCBC-MAC M 1 M 2 Mt K 2 if original block =128 K 3 if original block <128 IV = 0 K 1 Last block with padding (100…) E . . . E H 1 H 2 E Ht-1 Ht MAC Key derivation from the secret key K (Ipsec: AES-XCBC-MAC-96) K 1 = EK(0 x 0101010101010101) K 2 = EK(0 x 0202020202020202) K 3 = EK(0 x 0303030303030303) 42

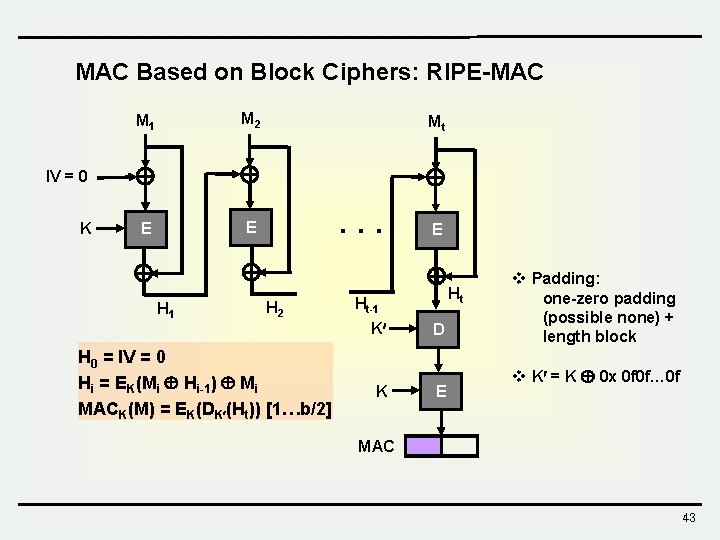
MAC Based on Block Ciphers: RIPE-MAC M 1 M 2 E E Mt IV = 0 K H 1 . . . H 2 H 0 = IV = 0 Hi = EK(Mi Hi-1) Mi MACK(M) = EK(DK (Ht)) [1…b/2] E Ht Ht-1 K K D E v Padding: one-zero padding (possible none) + length block v K = K 0 x 0 f 0 f… 0 f MAC 43

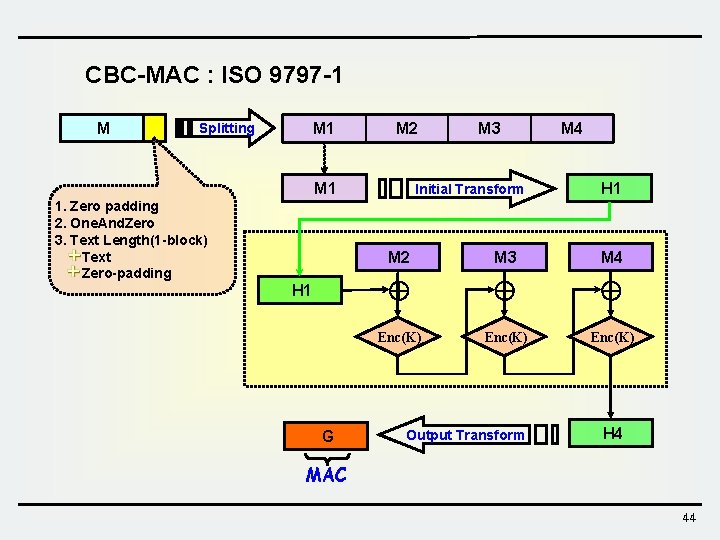
CBC-MAC : ISO 9797 -1 M M 1 Splitting M 2 M 1 1. Zero padding 2. One. And. Zero 3. Text Length(1 -block) Text Zero-padding H 1 G M 3 Initial Transform M 4 H 1 M 2 M 3 M 4 Enc(K) Output Transform H 4 MAC 44

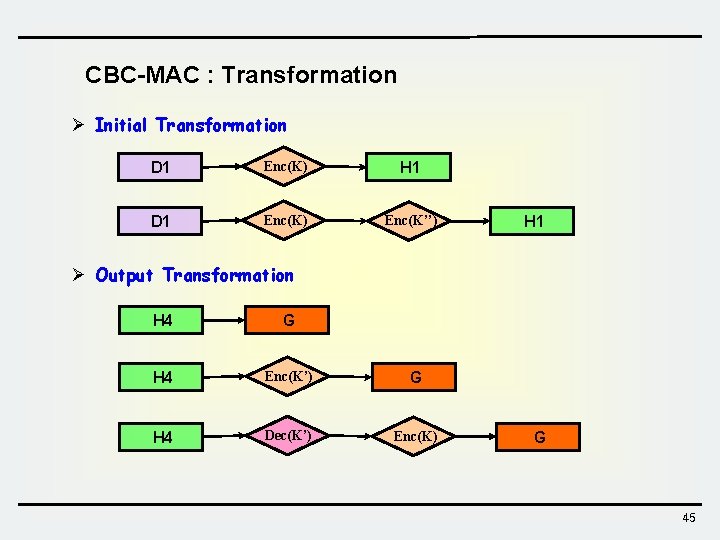
CBC-MAC : Transformation Ø Initial Transformation D 1 Enc(K) H 1 D 1 Enc(K) Enc(K’’) H 1 Ø Output Transformation H 4 G H 4 Enc(K’) G H 4 Dec(K’) Enc(K) G 45

Homework #2 Ø Hash Functions and its Implementation 2 nd Half : Select one of SHA-3 (round 1) candidates and program it with your favorite language. (Test: validation of given test vector) Deadline : 7/31, 2009 1. 2. 3. Describe why you choose X-hash Implement a C program (or use any language you prefer) which can encrypt and decrypt message in your algorithm Provide a performance analysis of your algorithm and your implementation 46