Introduction to Infinite Games Chapter 2 in Automata

Introduction to Infinite Games Chapter 2 in “Automata, Logic and infinite games” Jonathan Cederbaum

Infinite Games - Intro • 2 Players • Game board is a (possibly infinite) directed Graph • We Define: – How the games is played – Who wins • Determinacy, Winning Strategies, Forgetful Strategies, Memoryless Strategies • Fundamental Results

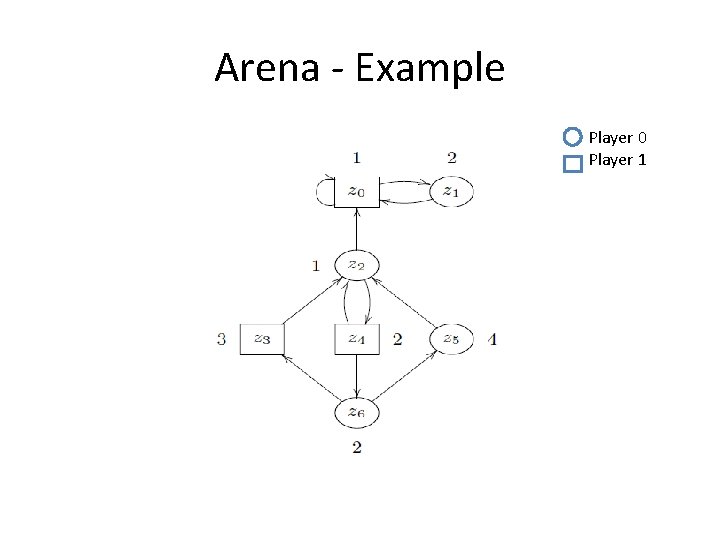
Games • Game: Arena + Winning Conditions • Arena: (V 0, V 1, E) (V = V 0 U V 1, E contained in Vx. V) • Successors of v in V: – v. E : = { v’ ∈ V | (v, v’) ∈ E } – May be infinite • 2 Players: Player 0, Player 1 – Notation: Player σ, Player σ where σ ∈ {0, 1} • Note: (V, E) not necessarily bipartite

A Play – Informal Explanation • The token is placed on some Initial vertex v. • If v is a 0 -Vertex, its Player 0’s turn. – Otherwise, it’s a 1 -Vertex, and Player 1’s turn. • On each turn, the player moves the token to some successor v in v. E. • Note: a player may play mutiple turns in concession. • The game goes on infinitely or until reaching a vertex without successors, a Dead End. – v. E = ∅.

A Play – Formal Definition • A Prefix of a Play defined as expected

Arena - Example Player 0 Player 1

Games & Winning Sets • A Game G is a pair: (A, Win) – A is the arena – Win ⊆ Vω is the Winning Set. • Player 0 is the winner of a play π in the game G iff: – π is a finite play: π = v 0 v 1…vr and vr is a 1 -vertex where Player 1 can’t move anymore (Dead end). – π is an infinite play and π ∈ Win • Note: Player 1 wins if Player 0 doesn’t. • In an Initialized Game (G, v. I) all plays start in v. I

Winning Conditions • How do we define the winning set (“Win”) ? • Use acceptance conditions of w-automata, to define a winning play. • Problem: the graph may be infinite, might not even have recurring states. . • Solution: color each vertex (Finite set of colors), – Apply acceptance conditions on the color sequence induced by the play.

Winning Conditions - Cont • A Coloring Function: χ: V C – C is some finite set of “colors” • Given a play: π = v 0 v 1 v 2… • Define the play’s coloring: χ(π)= χ (v 0)χ(v 1)χ(v 2)… • C (the color set) is viewed as the state set of a finite wautomaton. • Acc is the acceptance condition for this automaton. (As defined in the previous lecture) – buchi, muller, Rabin, Street, etc. • Wχ (Acc) : Defines the winning set to be all plays π where χ(π) is accepted according to Acc. – note dependence on χ

Acceptance Conditions • Buchi: (acc=F⊂P(C)) • π ∈ Wχ(Acc) iff Inf(χ(π)) ∩ F ≠ ∅ • Muller: (acc=F⊂2 C). • π ∈ Wχ(Acc) iff Inf(χ(π)) ∈ F • Max-Parity: C is some set of integers. • π ∈ Wχ(Acc) iff Max(Inf(χ(π))) is Even • Additional Acceptance Conditions: • Rabin, Rabin Chain Condition, Street etc. • A game is a regular game if its winning set equals Wχ(Acc) for some χ, and some Acc from above. • Notation: we write (A, χ, Acc) instead of (A, Wχ(Acc))

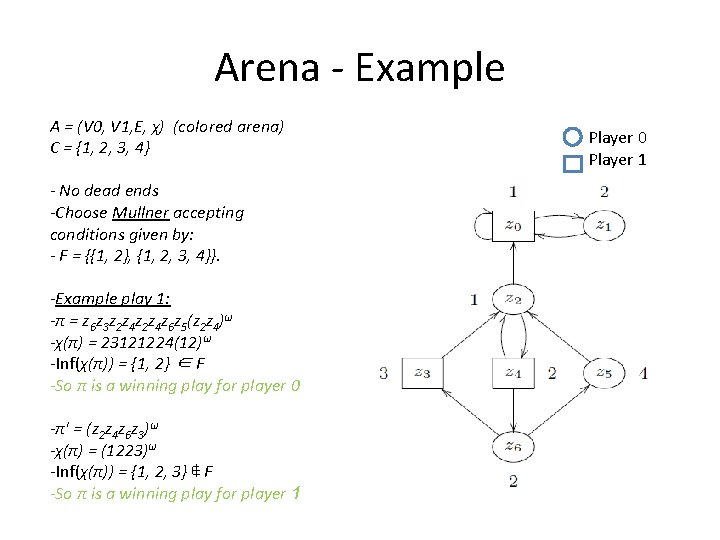
Arena - Example A = (V 0, V 1, E, χ) (colored arena) C = {1, 2, 3, 4} - No dead ends -Choose Mullner accepting conditions given by: - F = {{1, 2}, {1, 2, 3, 4}}. -Example play 1: -π = z 6 z 3 z 2 z 4 z 6 z 5(z 2 z 4)ω -χ(π) = 23121224(12)ω -Inf(χ(π)) = {1, 2} ∈ F -So π is a winning play for player 0 -π' = (z 2 z 4 z 6 z 3)ω -χ(π) = (1223)ω -Inf(χ(π)) = {1, 2, 3} ∉ F -So π is a winning play for player 1 Player 0 Player 1

Fundamental Questions I • Given an initialized game can one player win regardless of what the other does? – In this case we say the game is determined. – We will formalize this question by introducing the notions of a strategy, and a winning strategy. – The answer is yes, every (regular) game is determined (this result will be proved in chapter 6).

Fundamental Questions II • Given a final graph, can we compute who the winner is? Can compute it efficiently? – This and more – in chapter 7, stay tuned. – Complexity of determining the winner depends on the type of the game (The winning condition).

Fundamental Questions III • What does the winning strategy look like? – A general strategy tells the player the next move to make given all previous moves. – When might we have a winning strategy that requires remembering a bounded number of moves a Forgetful Strategy. – When can we decide the next move given just the current vertex - a Memoryless Strategy. – Answer: • regular games have Forgetful winning strategies. • Parity games have Memoryless winning strategies.

Strategies • • • A is an arena. σ ∈ {0, 1}. fσ : V*Vσ → V - a partial function. • A prefix of a play π = v 0 v 1…vr conforms with fσ if for every i, where 0 ≤ i ≤ r-1 and vi ∈ Vσ , the function fσ is defined at v 0…vi and: vi+1 = fσ(v 0 …vi). • A Play conforms with fσ if all its prefixes conform with fσ. • fσ is a strategy for Player σ on U ⊆ V if it is defined for every prefix of a play which starts in U, conform with it, and doesn’t end in a Dead End of Player σ. • When U is a singleton {v} we say fσ is a strategy for Player σ on v. • fσ is a Winning Startegy for Player σ on U if all plays which conform to fσ and start in U are wins for Player σ.

Strategies - Cont • Player σ wins a game G on U ⊆ V if he has a winning strategy on U. • When (G, v. I ) is an initialized game, we say Player σ wins it if he wins G on the singleton set {v}. • Given a game G, we define the winning region for Player σ, denoted Wσ(G), or Wσ for short, to be the set of all vertices v such that Player 0 wins (G, v). • Remark: For any game G, Player σ wins G on Wσ(G). – Since if Player σ wins on each group A ∈ T, then Player σ wins on U A.

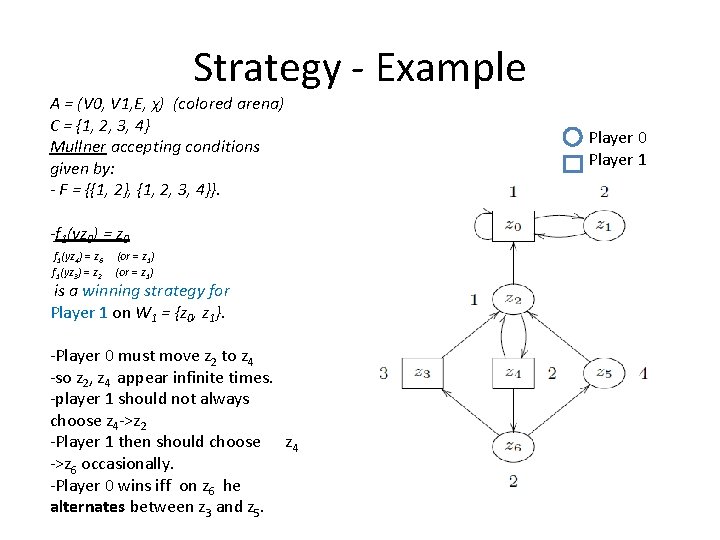
Strategy - Example A = (V 0, V 1, E, χ) (colored arena) C = {1, 2, 3, 4} Mullner accepting conditions given by: - F = {{1, 2}, {1, 2, 3, 4}}. -f 1(yz 0) = z 0 f 1(yz 4) = z 6 f 1(yz 3) = z 2 (or = z 1) is a winning strategy for Player 1 on W 1 = {z 0, z 1}. -Player 0 must move z 2 to z 4 -so z 2, z 4 appear infinite times. -player 1 should not always choose z 4 ->z 2 -Player 1 then should choose z 4 ->z 6 occasionally. -Player 0 wins iff on z 6 he alternates between z 3 and z 5. Player 0 Player 1

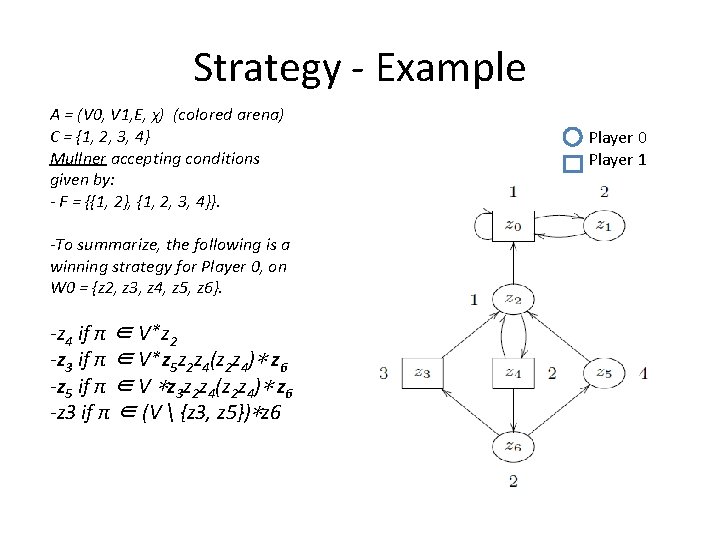
Strategy - Example A = (V 0, V 1, E, χ) (colored arena) C = {1, 2, 3, 4} Mullner accepting conditions given by: - F = {{1, 2}, {1, 2, 3, 4}}. -To summarize, the following is a winning strategy for Player 0, on W 0 = {z 2, z 3, z 4, z 5, z 6}. -z 4 if π ∈ V∗ z 2 -z 3 if π ∈ V∗ z 5 z 2 z 4(z 2 z 4)∗ z 6 -z 5 if π ∈ V ∗z 3 z 2 z 4(z 2 z 4)∗ z 6 -z 3 if π ∈ (V {z 3, z 5})∗z 6 Player 0 Player 1

Reduction of Muller Games to Parity Games • Note: For every regular game (A, χ, Acc) there exists a Muller winning condition Acc’ such that (A, χ, Acc) and (A, χ, Acc’) have the same winning regions. e. g for Buchi games define: F ‘: = {G ∈ 2 C | G ∩ F = ∅}. • Result: For every Muller game G=(A, χ, F) there exists a (max) parity game G’=(A’, χ’, Acc’) and an injection r : V → V’ such that every (unique) play π in G starting in v ∈ V induces a (unique) play π’ in G’ starting in r(v), and Player σ wins π in G iff he wins π’ in G’. – this result explains why we focus on Parity Games in chapter 6 & 7 • Remainder: – Muller: (acc=F⊂2 C). • π ∈ Wχ(Acc) iff Inf(χ(π)) ∈ F – Max-Parity: C is some set of integers. • π ∈ Wχ(Acc) iff Max(Inf(χ(π))) is Even

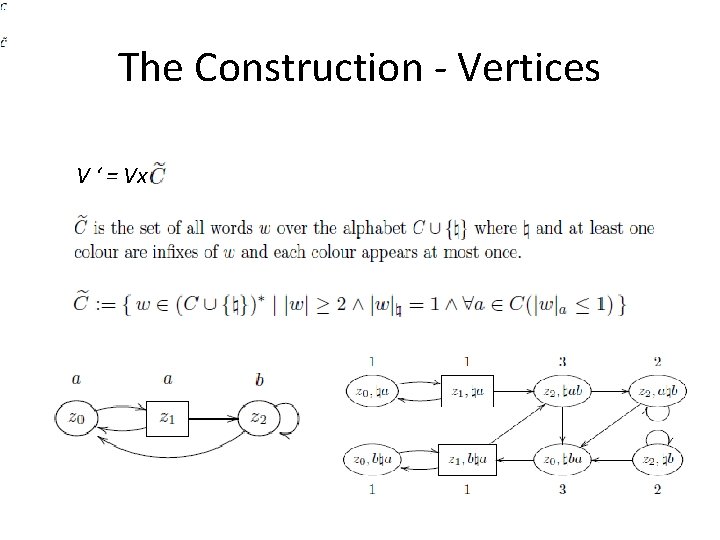
The Construction - Vertices V ‘ = Vx

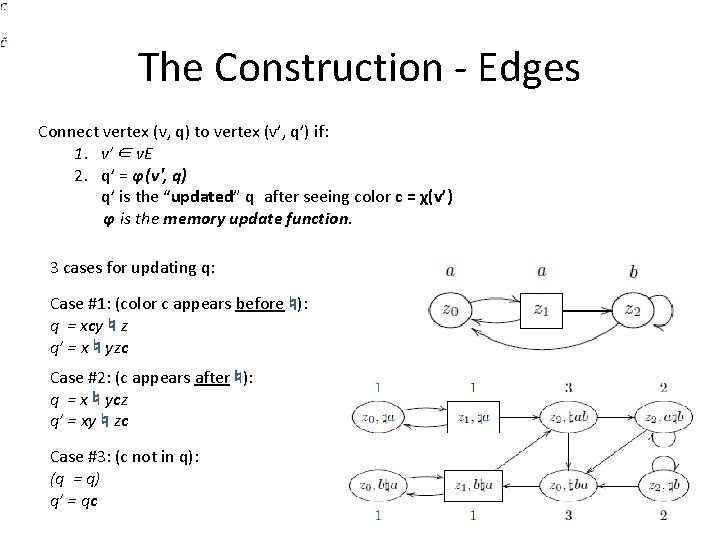
The Construction - Edges Connect vertex (v, q) to vertex (v’, q’) if: 1. v’∈ v. E 2. q’ = ϕ(v', q) q’ is the “updated” q after seeing color c = χ(v’) ϕ is the memory update function. 3 cases for updating q: Case #1: (color c appears before ♮): q = xcy ♮ z q’ = x ♮ yzc Case #2: (c appears after ♮): q = x ♮ ycz q’ = xy ♮ zc Case #3: (c not in q): (q = q) q’ = qc

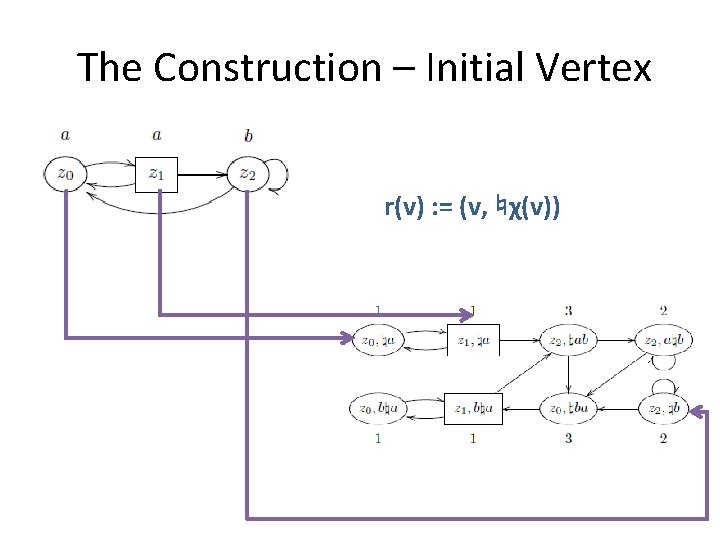
The Construction – Initial Vertex r(v) : = (v, ♮χ(v))

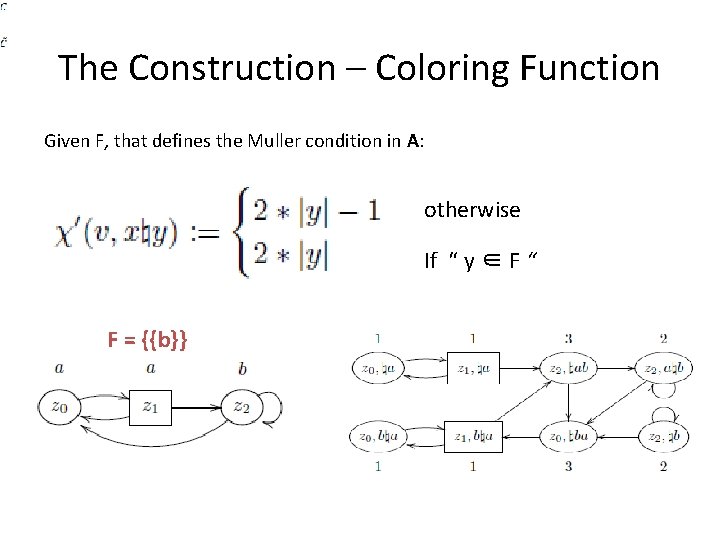
The Construction – Coloring Function Given F, that defines the Muller condition in A: otherwise If “ y ∈ F “ F = {{b}}

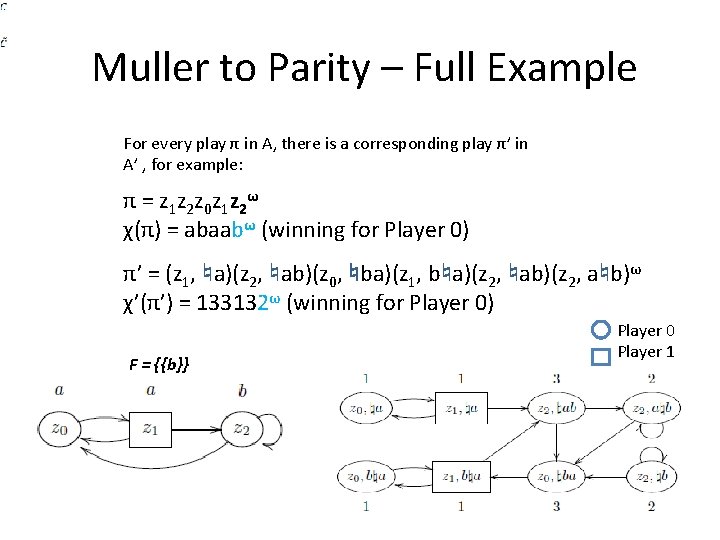
Muller to Parity – Full Example For every play π in A, there is a corresponding play π’ in A’ , for example: π = z 1 z 2 z 0 z 1 z 2 ω χ(π) = abaabω (winning for Player 0) π’ = (z 1, ♮a)(z 2, ♮ab)(z 0, ♮ba)(z 1, b♮a)(z 2, ♮ab)(z 2, a♮b)ω χ’(π’) = 133132ω (winning for Player 0) F = {{b}} Player 0 Player 1

Correctness of Construction • Theorem: For every Muller game (A, χ, F) there exists a (max) parity game (A’, χ’, Acc’) and a function r : V → V’ such that for every v ∈ V, Player σ wins ((A, χ, F), v) if and only if Player σ wins ((A’, χ’, Acc’), r(v)). • • π = v 0 v 1… ∈ Vω – infinite play in A. π’ – the corresponding play in A’ – – • • From some i ∈ ω colors not in F do not appear in π. at some j > i we have seen again all colors in F. at that point colors in F appear on the right side of the string. from step j+1 only colors in F appear right of the ♮. conclusion: |yi| ≤ |F| from some i ∈ ω since the left most color in F must appear at some point conclusion: there are infinite times k where | yk | = |F| and Thus the largest length of y that appears infinitely often is |F| and “y=F” –> the highest color that appears infinite times is: – – • qi = xi ♮ yi is defined by: q 0 : = ♮ χ(v 0) and qi+1 : = ϕ (vi+1, qi) for i ∈ ω. Argument 2: There are infinite times where all colors in F are right of the ♮. – – • ω where F : = Inf(χ(π)) Argument 1: from some point only c ∈ F appear on the right of the ♮. – – – • p 1(π’ ) = π p 2(π’ ) = q 0 q 1. . . ∈ 2*|F| if y ∈ F (even) 2*|F| - 1 if not (odd) Summary: π is winning for player 0 in A iff π’ is winning for him in A’. So Player 0 Wins (A, v) iff he wins (A’, r(v))

Determinacy • In all examples so far, the Winning regions for Player 0 and Player 1 partition V. • When a game has this property we say it is determined. • Theorem: Every parity game is determined. – proven in chapter 6. • Corollary: Every regular game is determined – (by the equivalence result proven earlier).

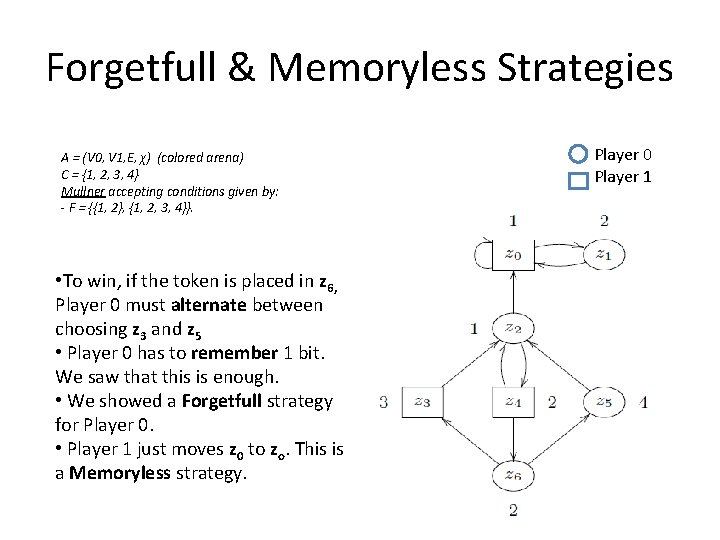
Forgetfull & Memoryless Strategies A = (V 0, V 1, E, χ) (colored arena) C = {1, 2, 3, 4} Mullner accepting conditions given by: - F = {{1, 2}, {1, 2, 3, 4}}. • To win, if the token is placed in z 6, Player 0 must alternate between choosing z 3 and z 5 • Player 0 has to remember 1 bit. We saw that this is enough. • We showed a Forgetfull strategy for Player 0. • Player 1 just moves z 0 to zo. This is a Memoryless strategy. Player 0 Player 1

Forgetful Strategies - Definition • A Strategy fσ is said to be forgetful (finite memory) if there exists: – – A finite set M An element m. I∈ M (the initial memory value) A function δ: V × M → M (memory update function) A function g: V × M → V (next move function) such that when π = v 0 v 1…vr is a prefix of a play, in the domain of fσ , and the sequence: m 0, m 1, . . . , mr is determined by m 0=m. I and mi+1= δ(vi+1, mi), then fσ (π)=g(vr , mr). • A forgetful strategy where |M|=1 is called Memoryless. – notation: fσ: Vσ → V

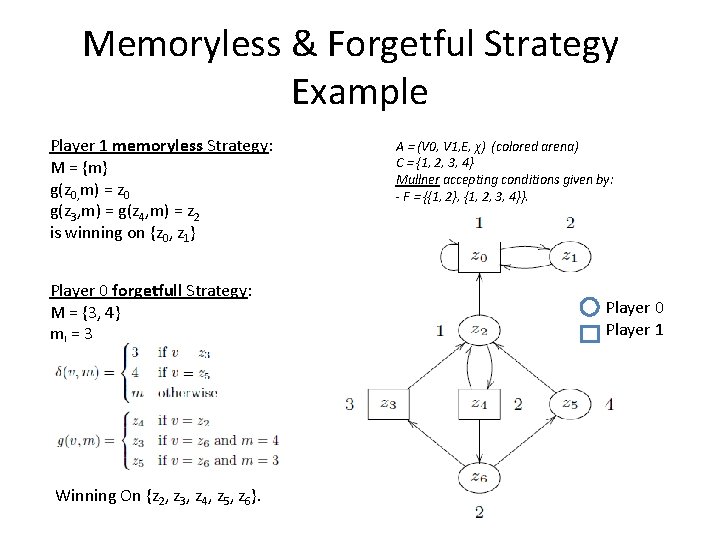
Memoryless & Forgetful Strategy Example Player 1 memoryless Strategy: M = {m} g(z 0, m) = z 0 g(z 3, m) = g(z 4, m) = z 2 is winning on {z 0, z 1} Player 0 forgetfull Strategy: M = {3, 4} m. I = 3 Winning On {z 2, z 3, z 4, z 5, z 6}. A = (V 0, V 1, E, χ) (colored arena) C = {1, 2, 3, 4} Mullner accepting conditions given by: - F = {{1, 2}, {1, 2, 3, 4}}. Player 0 Player 1

Forgetful Strategies – Cont. • Player σ wins a game G forgetful when he has a (maybe different) forgetful winning strategy for each point in his winning region. – winning a game G memoryless is defined accordingly. • Exercise: Give an example for a game G such that Player 0 wins forgetful on each {v} for v ∈ W 0, but he has no (single) forgetful winning strategy on W 0. – this is in contrast to the result on “regular” strategies. • The Lemma following shows that the statement is true for memoryless strategies (under certain conditions).

Lemma • Let G=(A, Win) by any game such that: 1. V (vertex set) is countable 2. V*Win ⊆ Win (adding a finite prefix) 3. Win/V*⊆ Win (removing a finite prefix) • Win/V ∗ : = { η ∈ Vω | ∃w ∈ V∗ with wη ∈ Win } • Let U be a set of vertices that Player σ has a memoryless winning strategy on each u ∈ U. • Then Player σ has a memoryless winning strategy on (all) U. – Condition 2 & 3 are satisfied for every regular game since Inf(X(π)) is unaffected.

Lemma – Proof (construction) • goal: construct a memoryless winning strategy on U. • for every u∈U, Let fσu : Vσ → V be a memoryless winning strategy for Player σ on u. – wlog assume the domain of fσu , denoted Du is minimal. • Let < be a well ordering on U (V is countable) • Define • For each v ∈ D, let u(v) be the minimal vertex in U s. t the strategy for u is defined for v. – • Define strategy: fσ(v) : = fσ u(v) – choose the “minimal strategy” defined for v

Lemma – Proof (correctness) • Need to show that fσ(v) : = fσ u(v) is a winning strategy on U. • Let π = v 0 v 1… be a play, starting in U and conforms with fσ. • In each σ-vertex vj in π, Player σ chooses fσ u(vj) • Let • Then from i on, fσ = fσu(vi) • vivi+1… is a suffix of a play π’ that starts in u(vi), visits vi , and conforms to fσu(vi) – by minimality of Du(vi) • Then π ∈ V∗(Win/V ∗) • And so, by condition 2 & 3 π ∈ Win

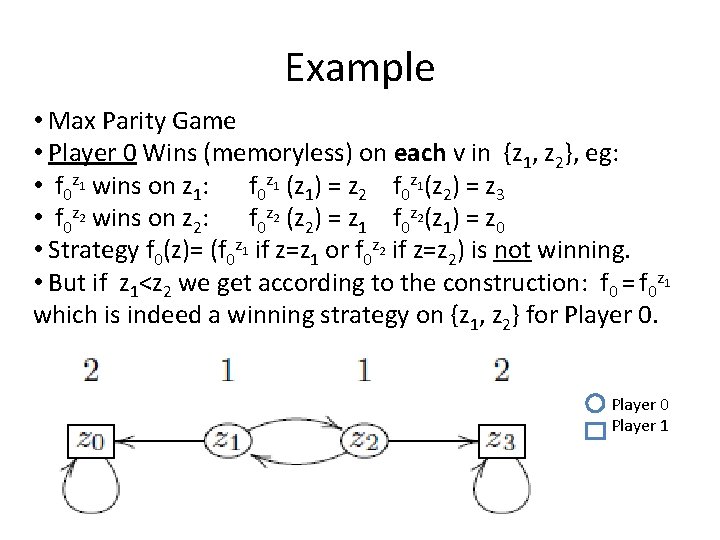
Example • Max Parity Game • Player 0 Wins (memoryless) on each v in {z 1, z 2}, eg: • f 0 z 1 wins on z 1: f 0 z 1 (z 1) = z 2 f 0 z 1(z 2) = z 3 • f 0 z 2 wins on z 2: f 0 z 2 (z 2) = z 1 f 0 z 2(z 1) = z 0 • Strategy f 0(z)= (f 0 z 1 if z=z 1 or f 0 z 2 if z=z 2) is not winning. • But if z 1<z 2 we get according to the construction: f 0 = f 0 z 1 which is indeed a winning strategy on {z 1, z 2} for Player 0 Player 1

Forgetful Determinacy of Regular Games • We prove: In every Regular Game both Players win forgetful. – “Forgetfull determinacy of Regular games” • We use the following theorem: In every Parity game, both players win memoryless. (proven in chapter 6) – “memoryless determinacy of parity games”

Forgetful Determinacy of Regular Games – Proof • Let (A, χ, F) be a Muller game – remainder: a regular game (A, χ, acc) has the same winning regions as some muller game (A, χ, F) • Let A’ be the “equivalent” Max-Parity game – V‘ = V × … • Let f’ 0, f’ 1 be memoryless winning strategies on W 0’, W 1’ – by “memoryless determinacy of parity games” • idea: use finite memory to simulate playing on A’ when playing on A. • Winning regions are: Wσ = { v ∈ V | (v, r(v)) ∈ W’σ}

Forgetful Determinacy of Regular Games – Proof • set memory M= • set m. I=r(v)= ♮ χ(v) • set δ=ϕ – update memory according to the update rule of 2. 7 • gσ(v, q) : = f’σ( (v, q) )0 ≡ (v’, q’)0 = v’ • f’σ generates a winning play in A’, then by previous theorem, the sequence of the first components is a winning play win A. – Thus gσ is a winning strategy for Player σ.

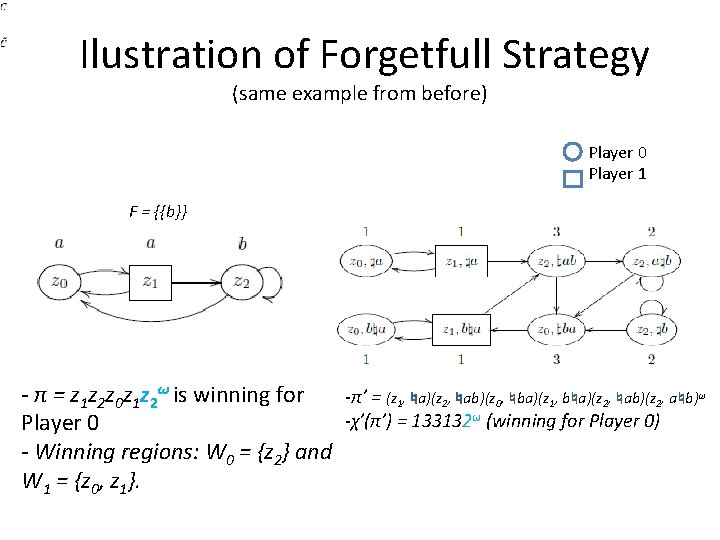
Ilustration of Forgetfull Strategy (same example from before) Player 0 Player 1 F = {{b}} - π = z 1 z 2 z 0 z 1 z 2ω is winning for -π’ = (z 1, ♮a)(z 2, ♮ab)(z 0, ♮ba)(z 1, b♮a)(z 2, ♮ab)(z 2, a♮b)ω -χ’(π’) = 133132ω (winning for Player 0) Player 0 - Winning regions: W 0 = {z 2} and W 1 = {z 0, z 1}.

Some (unproven) Results regarding memoryless determinacy • Parity games enjoy memoryless determinacy • In some Muller games both player need memory to win. • Rabin and Street are in between: one of the two players always has a memoryless winning strategy, specifically: – In Rabin games Player 0 has a memoryless strat. – In Streett games Player 1 has a memoryless strat.

Reachability Games & Attractors • A new kind of games, given: – Arena A = (V 0, V 1, E) – X⊆V • Reachability Game R(A, X): – π is a winning play for Player 0 if: • some v∈X occurs in π, or: • A dead end of Player 1 occurs in π. • Different then former games: dead end of player 0 isn’t necessarily a loss for him • strategies for player 0 aren’t required to be defined on plays ending in some v∈X.

Ordinals and Transfinite Induction – A Short Digression • Motivation: we want to prove some property using induction – Problem: dealing with non countable sets • Well Ordered sets: – A Totally ordered set, s. t each (non emtpy) subset has a least element. – equivalently (AOIC) every strictly descending series is finite – canonical example: ℕ • Ordinals: we think of them as the position of an element in an ordered set. – An ordinal that is no a successor (other then 0) is called a limit ordrinal. – Example: 0, 1, …, ω, ω+1, ω+2…, ω*2, … , ω*ω… • Theorem: every set can be well ordered (using AOC)

Transfinte induction (and recursion) • Induction: – prove P(0) (base case) – successor step: assuming P(a) prove P(a+1) – Limit step: for every limit ordinal λ assume P(a) for all ordinals λ<a to prove P(λ) • Recursion: – Define S 0 – for every ordinal a define Sa+1 using definition Sa – Limit step: for every limit ordinal λ define S λ using the definition of sa for all ordinals a<λ.

Theorem: Reachability Games Enjoy Memoryless Determinacy • A is an arena, X ⊆ V • The winning region and the winning strategy for player 0 in R(A, X) are defined inductively: – X 0 = X – For ordinals v: Xν+1 = Xv ∪ pre(Xv) • pre(Y ) = { v ∈ V 0 | v. E ∩ Y = ∅ } ∪ { v ∈ V 1 | v. E ⊆ Y } – vertices in V 0 who have a neighbour in Y – verticesi in V 1 where all neighbours are in Y. – for each limit ordinal ξ: • Idea: A ⊂ W 0 �A ∪ pre(A) ⊂ W 0 • Let ξ be the smallest ordinal such that Xξ = Xξ+1 • Claim: W: = Xξ is Player 0’s winning region (W=W 0).

Illustration 1ω=X 0 UPre(X 0) ω) 2 12 12 ω i. U Pre(X 03 =U X =X Xω+1 =X i

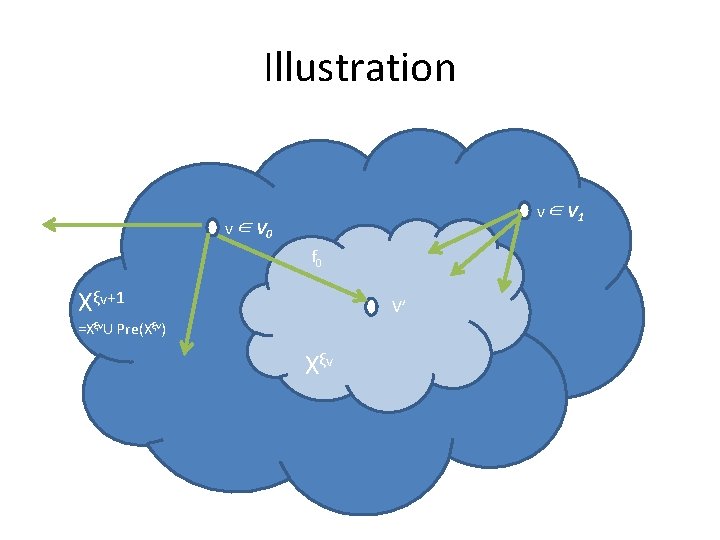
Reachability games enjoy memoryless determinacy – First Direction. • First direction, show W⊆W 0: • For every v ∈ WX there exists a unique ordinal ξv < ξ such that v ∈ Xξv+1 Xξv • Further, if v∈V 0 (v∈W∩V 0X) then by Pre there is a neigbour of v, v’ s. t v’∈ Xξv • Choose (memoryless) strategy: f 0(v) = v’ • Claim: f 0 is winning on W. – Show by transfinite induction: f 0 is winning on Xν for every ν ≤ ξ.

Illustration v ∈ V 1 v ∈ V 0 f 0 Xξv+1 V’ =Xξv. U Pre(Xξv) Xξ v

Reachability games enjoy memoryless determinacy – Second direction. • • • Define W’ = VW. Second direction: show W’ ⊆ W 1 Let v∈ W’ – v∉ X If v is a dead end: – It is a dead end of Player 0 – Since all dead ends of player 1 are in X 1 (by Pre) – Then player 1 win on v If v is not a dead end and v ∈ V 0: – then for every v’ ∈ v. E v’ ∉ W (v’ ∈ W’) If v is not a dead end v ∈ V 1: – there exists v’ ∈ v. E such that v’ ∉ W (v’ ∈ W’) Set f 1(v) = v’ (memoryless strategy for Player 1) Every play conform with f 1 and starting in W’ is contained in W’ Since W’ doesn’t contain vertices from X or dead ends of Player 1, every such play is winning for Player 1. Finally: W=W 0 and W’=W 1

Reachability Games-definitions • The winning region of Player 0 in the reachability game R(A, X) is denoted Attr 0(A, X) and called 0 -attractor of the set X in the arena A. • The winning strategy (denoted f 0 in the proof) is called the a corresponding attractor strategy for Player 0. • 1 -attractor and strategy are symmetrically defined by exchanging V 0 and V 1 in the arena.

σ-trap - Definition • A σ-trap is a subset Y ⊆ V such that v. E ⊆ Y for every v ∈ Y∩Vσ and v. E∩Y ≠ ∅ for every v∈Y∩Vσ • A function which picks for every v∈Y∩Vσ a vertex v’∈ v. E ∩ Y is called a trapping strategy for Player σ. • The complement of a σ-attractor is a σ-trap – in last proof W’=VW is a 0 -trap.

Conclusion – WLOG arenas have no dead ends (no proof) • Let (A, Acc) be an arbitrary game – A = (V 0, V 1, E) • set Uσ = Attrσ(A, ∅) – Player σ wins on Uσ Memoryless (by forcing the player σ to a dead end) • Arena A’: remove vertices from which you can force the other player to a dead end: – – – • V 0’ : = V 0 (U 0∪ U 1) V 1’ : = V 1 (U 0∪ U 1) V’ = V 0’ ∪ V 1’ E’ = E∩(V’x. V’) A’ = (v 0’, v 1’, E’) Claim: for every v∈ V’, Player σ wins (A’, Acc, v) iff he wins (A, Acc, v) – – – Winning strategies for (A’, Acc) can be used in (A, Acc). use: “the complement of a σ-attractor is a σ-trap” hw. .

Memoryless determinacy in Buchi games • As mentioned, all regular games enjoy memoryless determinacy (chapter 6). • We show a simple proof for Buchi games. • Remainder - Buchi acceptance condition: (Acc = F ⊆ C): π ∈ Wχ(Acc) iff Inf(χ(π)) ∩ F = ∅.

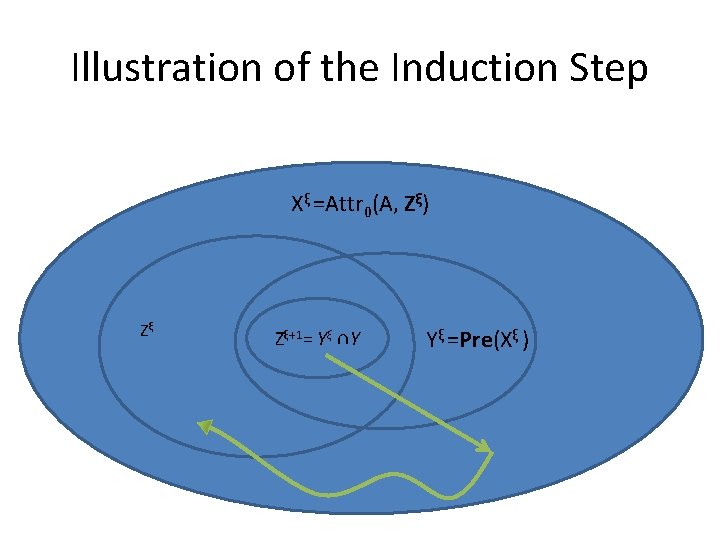
Memoryless Determinacy in Buchi Games - Construction • Inductive construction of a winning region for Player 0 in the Buchi game (A, χ, F): – – – set Y : = χ− 1(F) Z 0 =V (all vertices) Xξ = Attr 0(A, Zξ) Yξ = Pre(Xξ) Zξ+1 = Yξ ∩Y Zξ = (for limit ordinals ξ) • Let ξ be the least ordinal ≥ 1 s. t Zξ = Zξ+1 • Zξ ⊂Xξ �Xξ+1 =Attr 0(Zξ) ⊂ Attr 0(Xξ)=Xξ (by monotonicity of Attr 0) – • • Xξ+1 ⊂ Xξ Y ξ+1 ⊂ Yξ (by monotonicity of pre) Zξ+1 ⊂ Zξ • claim: W : = Attr 0(A, Zξ) is the winning region of player 0. (i. e W=W 0)

Illustration of the Induction Step Xξ =Attr 0(A, Zξ) Zξ Zξ+1= Yξ ∩Y Yξ =Pre(Xξ )

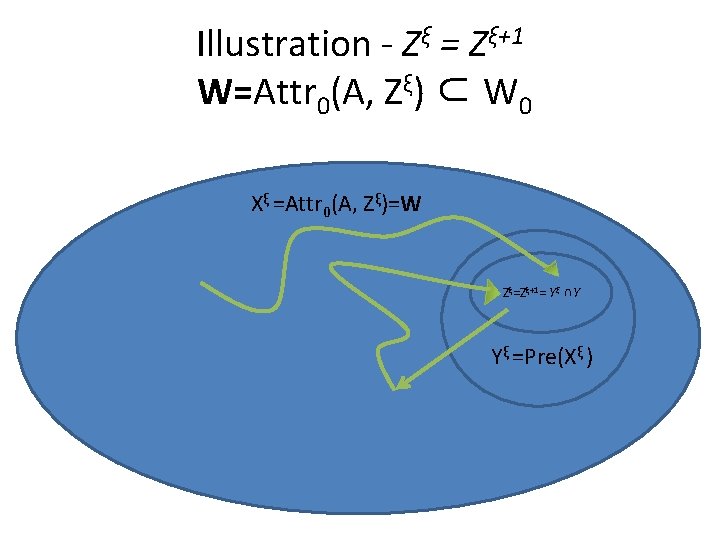
Illustration - Zξ = Zξ+1 W=Attr 0(A, Zξ) ⊂ W 0 Xξ =Attr 0(A, Zξ)=W Zξ=Zξ+1= Yξ ∩Y Yξ =Pre(Xξ )

Correctness - W⊆ W 0 • Define a memoryless winning strategy for Player 0 on W: • For every v∈ V 0∩Zξ, there exists v’∈ v. E∩Attr 0(A, Zξ) – since Zξ = Zξ+1 = Yξ ∩Y= Pre(Xξ) ∩ Y = Pre(Attr 0(A, Zξ)) ∩ Y – set f 0(v) = v’ • for other v∈ V 0∩W Zξ, v∈ W=Attr 0(A, Zξ): – set f 0(v) according to the respective attractor strategy • For a play starting in W, that conform with f 0: – If finite: must end in dead end of Player 1. – If infinite: must reach Zξ at some point, from that point it will reach Zξ infinite more times, Since Zξ⊆ Y (ξ ≥ 1) then it is a winning game for Player 0.

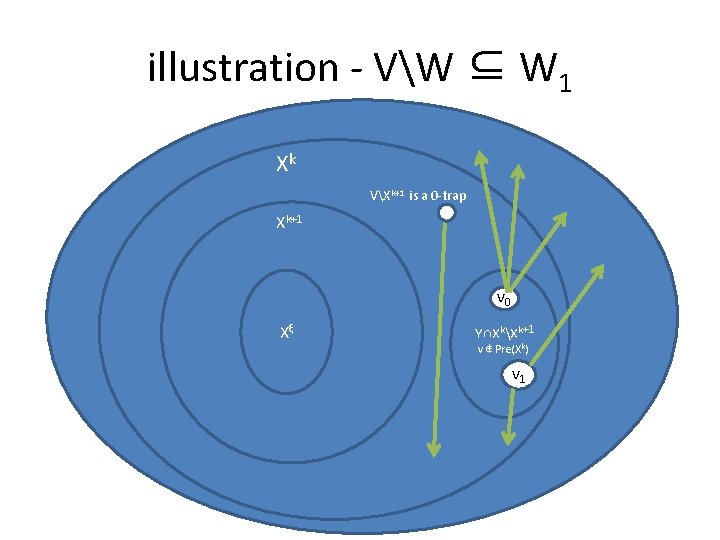
illustration - VW ⊆ W 1 Xk VXk+1 is a 0 -trap Xk+1 v 0 Xξ Y∩XkXk+1 v ∉ Pre(Xk) v 1

Correctness – VW ⊆ W 1 • We show a memoryless winning strategy on W’ : =VW • For each v ∈ W’ there’s a least k s. t v ∈ Xk Xk+1 – Since X 0=V – and Xi is decreasing in i ( Xa ⊆ Xb for every b < a) – (notice: W=Xξ ) • Xk+1 is a 0 -attractor (by def) so the complement VXk+1 is a 0 -trap. • If v ∉ Y: – If v ∈ V 1: Set f 1(v) according to the trapping strategy – If v ∈ V 0: Player 0 is trapped in VXk+1 • If v ∈ Y: then v ∉ Pre(Xk) ≡ Yk (v∈ Yk and v∈ Y v∈ Zk+1 v∈ Xk+1 ) • If v ∈ V 1: there exists v’∈ v. E and v’ ∉ Xk – • Set f 1(v) = v’ If v ∈ V 0: – For every v’∈ v. E and v’ ∉ Xk • Then f 1 is a a memoryless winning strategy for v ∈W’ (show by induction)

Summary • • What is a game, kinds of different games we saw that its “enough” to solve parity games. What is a strategy, a winning strategy Are there simple Strategies? – saw: if “every Parity Game both Players win memoryless” then “every Regular Game both Players win forgetful” • Showed directly that Buchi games enjoy memoryless determincay.