Introduction to Inferential Statistics Where have we been

Introduction to Inferential Statistics

Where have we been? • Epidemiology – the study of health events, circumstances, time and intervention • Causation & Correlation, Basics of Epidemiology • Study Designs & Research Process • Populations and Samples • Chance, rates and ratios

How and what can we infer from a sample to a population? • Process • • Research question Research hypothesis Descriptive statistics to organize observations Inferential statistics to reflect the characteristics from a sample to a population

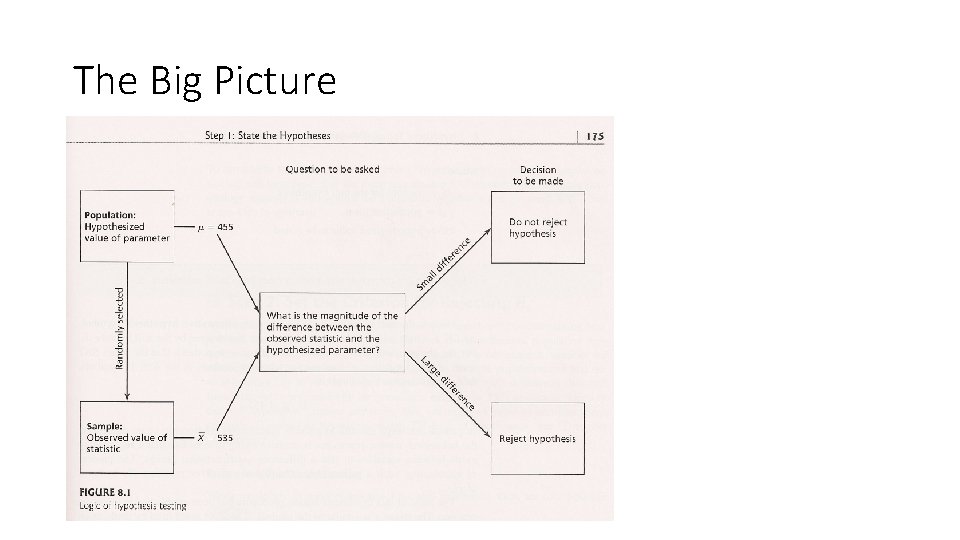
The Big Picture

Hypothesis Testing The Steps: 1. State Hypotheses (null, alternative) 2. Set Criterion for Rejection of Null Hypothesis • alpha level (usually set at 0. 05) 3. Compute test statistic (p-value of what you observed) 4. Compare computed test statistics (p value) with criterion (alpha level) 5. Make decision: Reject or fail to reject the null hypothesis The logic: • If A then B; • if not B, therefore, not A. • In a sentence: If A is true, then you would see something like B, but you did not see B, therefore, you reject A.

Key points about hypothesis testing • We always assume the null hypothesis is true. • Based on what we observed, we either reject the null or fail to reject the null (retain the null) • If we reject the null we support (not prove) the alternative hypothesis. • If we fail to reject the Null (retain), the Alternative Hypothesis is not tenable, or not supported

Quick walk through the Process • Step 1: State the hypothesis • Step 2: Set the alpha level • Step 3: Compute the test statistic • Step 4: Compare computed test statistic with criterion • Step 5: Make a decision

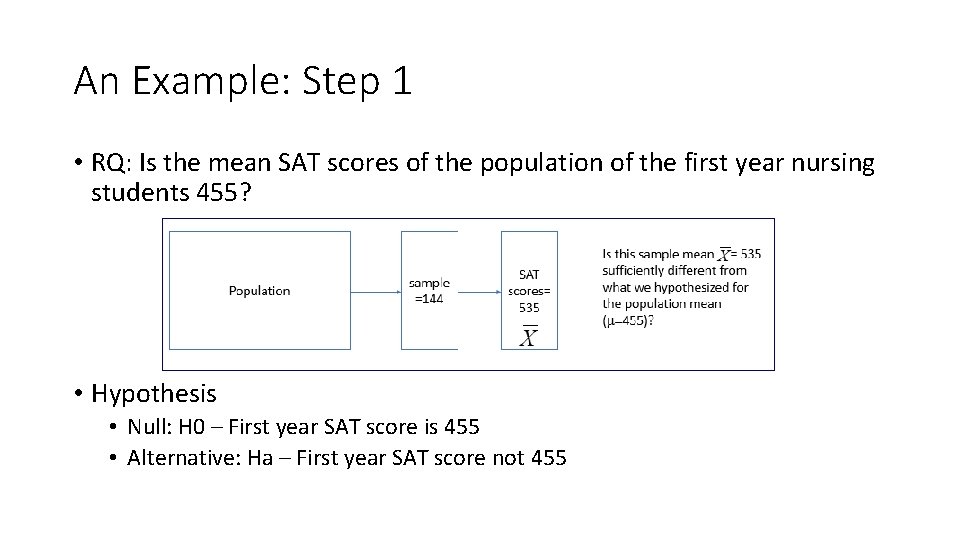
An Example: Step 1 • RQ: Is the mean SAT scores of the population of the first year nursing students 455? • Hypothesis • Null: H 0 – First year SAT score is 455 • Alternative: Ha – First year SAT score not 455

An Example: Step 2 • Set the Criterion (alpha level) for rejecting the null hypothesis • Always set the alpha level before any testing is completed • What does this criterion do? • Controls the amount of risk/uncertainty in the study • Alpha criterion limits the possibility of Type I error • Type I & Type II Error • Type I error (α) is when we reject a true null hypothesis; • Type II error (β) is when we do not reject a false null hypothesis. • Typical Alpha levels are. 10, . 05, and. 01 • 10% of the area under the probability curve • 5% of the area under the probability curve • 1 % of the area under the probability curve

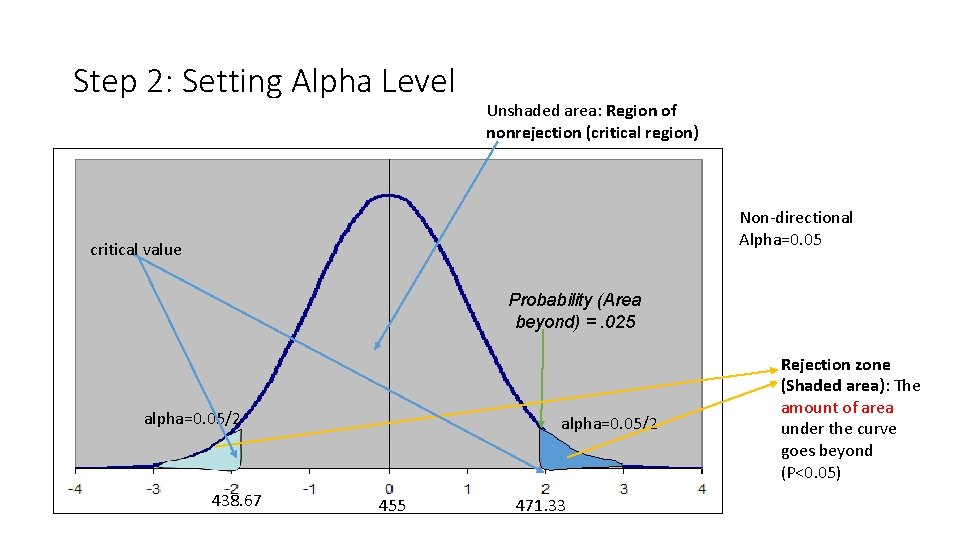
Step 2: Setting Alpha Level Unshaded area: Region of nonrejection (critical region) Non-directional Alpha=0. 05 critical value Probability (Area beyond) =. 025 alpha=0. 05/2 438. 67 alpha=0. 05/2 455 471. 33 Rejection zone (Shaded area): The amount of area under the curve goes beyond (P<0. 05)

Step 3: Compute the Test Statistic • Calculate the statistic (z scores) • Z score (other statistics values) VS. Critical value • Depending on what type of statistic testing method you selected, statistic values will be different, such as t value, F value. • P value • Confidence interval (we will discuss it later) Software will do the job for you!

Step 4/5 Compare computed test statistics with criterion and make decision • We compare our test statistic to the criterion • In our example: we reject H 0: • Ho : m = 455 • The mean SAT score (M = 535) of the 144 sample was significantly different from the hypothesized value of 455, Z(143) = 9. 60, p <. 05. • Z (9. 60) > criterion (1. 96) • Sample mean=535 • Falls into rejection area. • P<. 05

In this module… • Resources to review: • • Measures of Central Tendency P values and Confidence Intervals Type I & II Error Power • Study Guide • Flash cards • Examples from the literature to help you see these concepts in use