Introduction to Inference Estimating with Confidence IPS Chapter


























































- Slides: 77

Introduction to Inference Estimating with Confidence IPS Chapter 6. 1 © 2009 W. H. Freeman and Company

*** Overview Example p Researchers at a hospital want to know if a new drug is more effective than a placebo. Twenty patients receive the new drug, and 20 receive the old medication. Twelve (60%) of those taking the drug show improvement versus only 8 (40%) of the patients on the older drug. p Our unaided judgement would suggest that the new drug is better. However, probability calculations tell us that a difference this large (or even larger) between the results in the two groups would occur about 1 in 5 times purely by chance! This probability, 0. 2 (20%) is not considered to be very small. So rather than make any major changes in medication at the hospital, it is better to conclude that the observed difference is due to chance rather than to any real difference between the two medications. p Yes, the likelihood that this result was due to chance (a fluke) is only 20%. But it is STILL too high to ignore. p This example forms the entire basis for this chapter and is one of the most widely misunderstood concepts in statistics as it is applied to the real world. Review this example every little while as you study the chapter. It will help the ‘big picture’ to emerge. p In addition to understanding the big picture, you will also learn how to determine the probability that some result was due to chance (the “ 20%”) we came up with above.

Concept Overview p In this lecture we’ll discuss two of the most famous types of formal statistical inference. p Confidence Intervals (6. 1): This is where we estimate the value of a population parameter (by using sample data). § Recall that “parameter” is the term we use when referring to a population. “Statistic” is the term we use when referring to a sample. § p Eg: Mean fuel economy of all cars in America is a parameter. The mean of a random sample of 100 cars is a statistic. Tests of Significance (6. 2): Assessing the evidence for a claim. § Eg: How strongly we believe that the confidence interval calculated above really, truly does contain the population parameter that we are looking for.

Objectives (IPS Chapter 6. 1) Estimating with confidence p Statistical confidence p Confidence intervals p Confidence interval for a population mean p How confidence intervals behave p Choosing the sample size

SD of the Population p Important Note: This whole chapter assumes we know the population SD. In the real world, we often do NOT. However, the underlying concepts are the same. p A later section of the textbook has a discussion on how to do statistical inference and confidence intervals even when we don’t know the sd of the population.

* Overview of inference 1. Statistical inference is all about using the information from your sample to draw conclusions about your population. p p 2. Sample information Population information E. g. Average undergrad loan amount at De. Paul: Given a survey of 200 randomly sampled De. Paul students, what can we infer is the average loan amount for all De. Paul students? Once we’ve drawn a conclusion, a second extremely important aspect of inference is to express (in terms of probability) how much confidence we have in that conclusion.

* Substantiating our conclusions p We have already examined data and arrived at conclusions many times throughout the course. Formal inference emphasizes substantiating these conclusions by assigning probabilities to them. p That is, we need to take every conclusion and say just how confident we are that our conclusion is valid. We do this by assigning a probability to each conclusion that we make. p These probabilities come in the form of: p Confidence Intervals (discussed in section 6. 1) p Tests of Significance (discussed in section 6. 2)

An example to think about… p Suppose in your survey of 200 De. Paul students, you come up with a mean loan amount of $43, 842. Of the two options presented here, which do you think is likely to be the more accurate way of reflecting the true (ie: population) average loan amount? a) The population (all De. Paul students) mean is $43, 842 b) The population mean is somewhere between $41, 000 and $45, 000 I would suggest the second one. The reason is that the $43, 842 amount we came up with only comes from a single sample of students. Obviously a different example would give a different value. One option would be to take repeated samples. However, this is often very costly (time & money) so in the real world, we can’t do it. Instead, we take the value from our sample and with it, calculate a margin of error. This is the value that we report. All we are then saying is that “based on our sample, we believe the population (true) value is between $41, 000 and $45, 000.

Inference in different situations p Rules and types of inference differ depending on the situation. p In this chapter, we will focus on only one particular situation: p p Discussing the MEAN value (e. g. mean student debt, mean income, mean height, etc) p using data that follows a NORMAL distribution p where the standard deviation is KNOWN. Once you become comfortable applying inference rules to this particular situation, it is not all that difficult to learn the differences that must be used in other settings (e. g. non-Normal populations, populations with unknown SDs, etc).

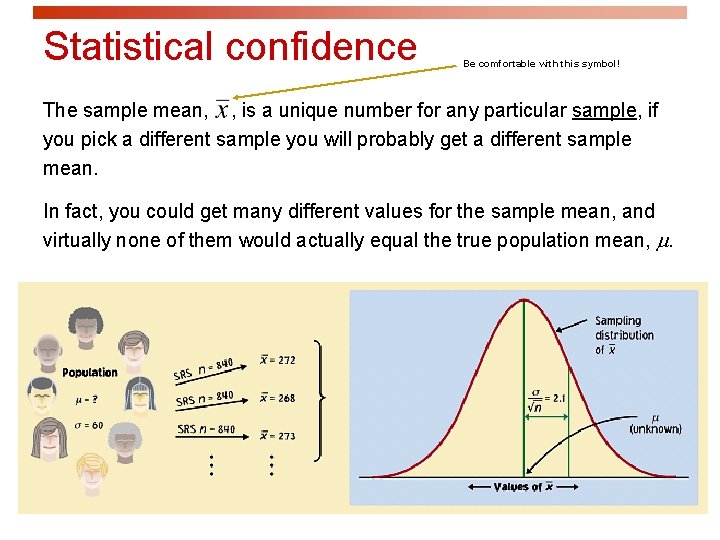
Statistical confidence Be comfortable with this symbol! The sample mean, , is a unique number for any particular sample, if you pick a different sample you will probably get a different sample mean. In fact, you could get many different values for the sample mean, and virtually none of them would actually equal the true population mean, .

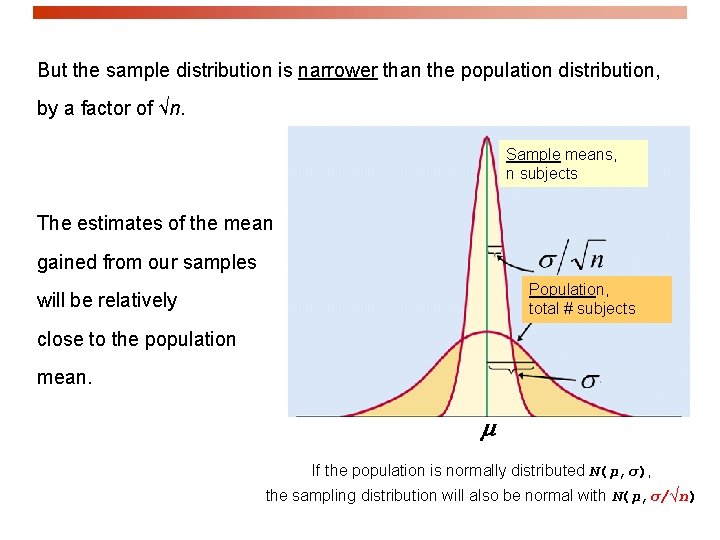
But the sample distribution is narrower than the population distribution, by a factor of √n. n Sample means, n subjects The estimates of the mean gained from our samples Population, total # subjects will be relatively close to the population mean. m If the population is normally distributed N(µ, σ), the sampling distribution will also be normal with N(µ, σ/√n)

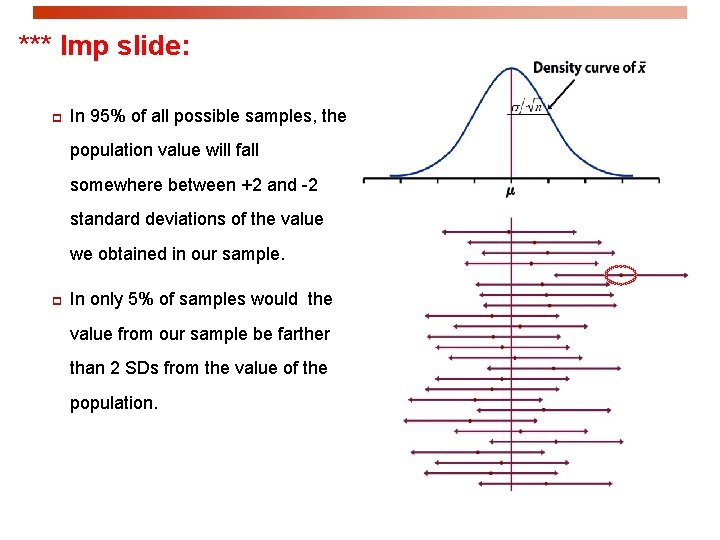
*** Imp slide: p In 95% of all possible samples, the population value will fall somewhere between +2 and -2 standard deviations of the value we obtained in our sample. p In only 5% of samples would the value from our sample be farther than 2 SDs from the value of the population.

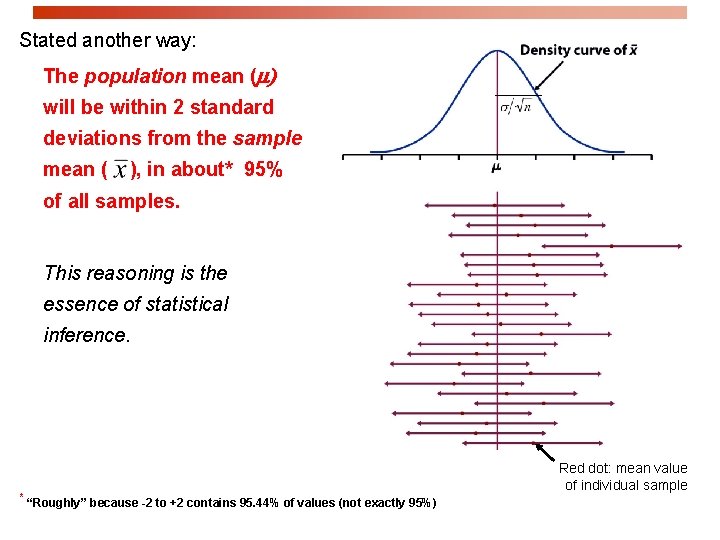
Stated another way: The population mean (m) will be within 2 standard deviations from the sample mean ( ), in about* 95% of all samples. This reasoning is the essence of statistical inference. * “Roughly” because -2 to +2 contains 95. 44% of values (not exactly 95%) Red dot: mean value of individual sample

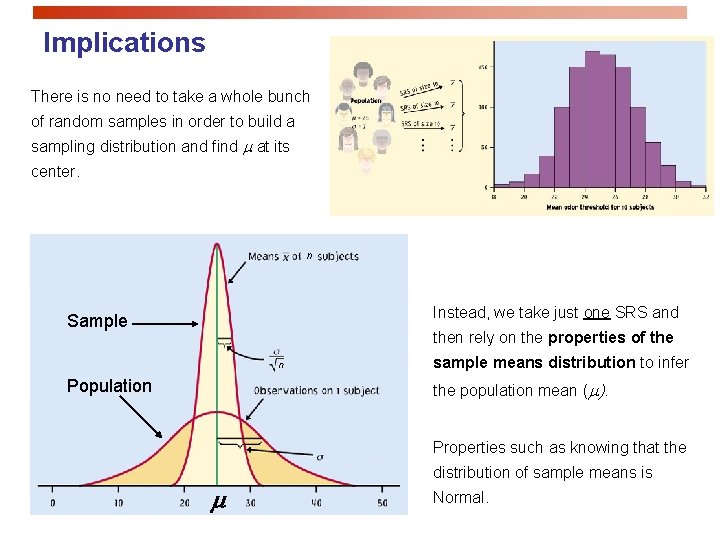
Implications There is no need to take a whole bunch of random samples in order to build a sampling distribution and find at its center. n Instead, we take just one SRS and Sample then rely on the properties of the n Population sample means distribution to infer the population mean ( ). Properties such as knowing that the m distribution of sample means is Normal.

The weight of single eggs of the brown variety is normally distributed N(65 g, *5 g). Think of a carton of 12 brown eggs as a single sample (SRS) of size 12. . p What is the distribution of the sample means ? p Recall that sample means follow a normal distribution, where the mean = the mean of your sample, and the SD = the population SD/square root of n. So: p Answer = N(65 g, 1. 44 g) p Find the middle 95% of the sample means distribution. ± 2 standard deviations from the mean, or roughly 65 g ± 2. 88 g. *RECALL: This whole chapter assumes we know the SD of the population.

A second sample: You buy a second of 12 eggs and find that the average egg weight from that SRS is 64 g. As discussed in the previous slide, we know the sd of the population of all eggs (5 g). According to this second sample, what is the distribution of (all) sample means? In what range does the middle 95% of all values lie? p N(64, 1. 44) p 95% of all sample means fall between 61. 12 and 66. 88 (64 g ± 2. 88) p Note that this sample gives a slightly different answer from the previous sample. This is to be expected: every sample is likely to have a different value for the mean.

* Overview: Confidence Interval p A range that we obtain by doing certain calculations on data from a sample. p p EXAMPLE: We look at a random sample of 1000 cars and do some calculations on their fuel consumption. We come up with a “confidence interval” that says the average fuel consumption ranges between 14. 2 and 16. 9 miles per gallon. Confidence Interval = 14. 2 – 16. 9 p The point is that we are pretty sure that the true population value lies somewhere inside this range. p But HOW sure? 100%? 50%? 95%? p p We need to quantify our degree of certainty that the confidence interval contains the true mean. (Ie: The population’s mean). We quantify this by the ‘Confidence Level’

Confidence intervals p The confidence interval is a range of values. p To that confidence interval, we assign a probability called the confidence level which we assign the symbol ‘C’. This probability quantifies the chance that the interval contains the true population parameter. ± 4. 2 is a 95% confidence interval for the population parameter . We are saying that: “In 95% of the cases, the actual value of m will be within 4. 2 units of the value of. ”

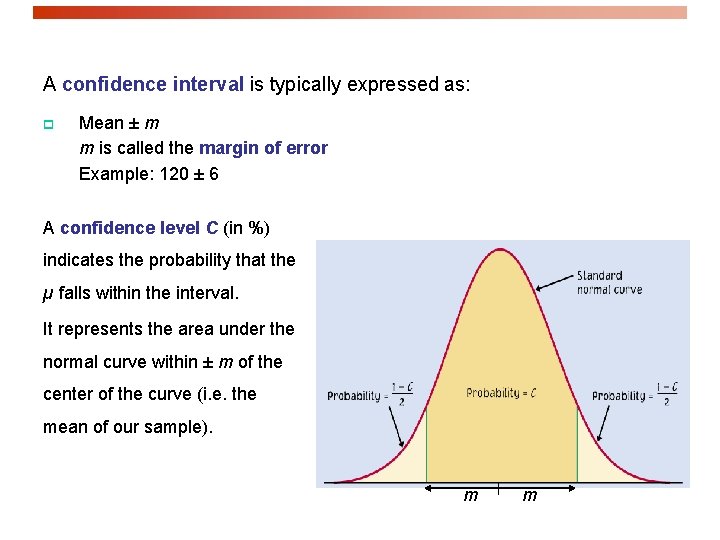
A confidence interval is typically expressed as: p Mean ± m m is called the margin of error Example: 120 ± 6 A confidence level C (in %) indicates the probability that the µ falls within the interval. It represents the area under the normal curve within ± m of the center of the curve (i. e. the mean of our sample). m m

Why choose 95% as our value for C? In fact, we can assign any value for C that we like. The most p commonly chosen one is 95%. p However, note that changing ‘C’ also changes ‘m’ p p If you want a higher confidence level (e. g. 99%), then you will have a to accept a wider margin of error. § Eg: At 95% you may have ± 4. 2 § At 99% you may have ± 6. 3 Restated: It’s great to have a higher confidence level, but the cost is that we now have a higher range for your margin of error. p Similarly, if you are willing to accept a lower confidence level (e. g. 90%), then you will have the benefit of a smaller margin of error: § Eg: At 95% you may have ± 4. 2 § At 90% you may have ± 2. 3

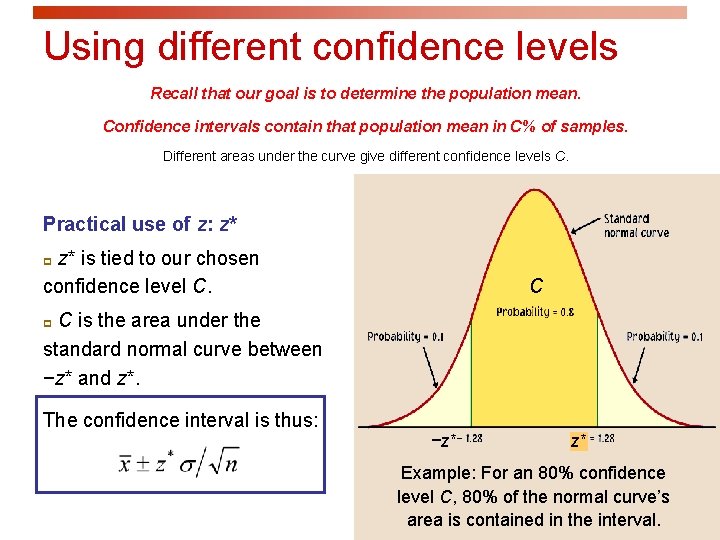
Using different confidence levels Recall that our goal is to determine the population mean. Confidence intervals contain that population mean in C% of samples. Different areas under the curve give different confidence levels C. Practical use of z: z* z* is tied to our chosen confidence level C. p C C is the area under the standard normal curve between −z* and z*. p The confidence interval is thus: −z* z* Example: For an 80% confidence level C, 80% of the normal curve’s area is contained in the interval.

* How do we find specific z* values? We can use a table of z/t values (Table D, bottom of page T-11). For a particular confidence level, C, the appropriate z* value is just above it. Example: For a 98% confidence level, z*=2. 326 We can also use software. Because the most common C that we use is 95%, it is almost worth memorizing the corresponding z* which is 1. 96. Confidence interval =

Link between confidence level and margin of error The confidence level C determines the value of z* (in table C). The margin of error also depends on z*. The tradeoff: Higher confidence C implies a larger margin of error m (thus less precision in our estimates). C A lower confidence level C produces a smaller margin of error m (thus better precision in our estimates). m −z* Review: What is our overall goal here? Answer: To predict a range of values that contains the population mean. m z*

Different confidence intervals for the same set of measurements Density of bacteria in solution: Measurement equipment has standard deviation = 1 * 106 bacteria/ml fluid. Three measurements: 24, 29, and 31 * 106 bacteria/ml fluid Mean: = 28 * 106 bacteria/ml. Find the 96% and 70% CI. p 96% confidence interval for the p 70% confidence interval for the true density, z* = 2. 054, and write true density, z* = 1. 036, and write = 28 ± 2. 054(1/√ 3) = 28 ± 1. 036(1/√ 3) = 28 ± 1. 19 x 106 bacteria/ml = 28 ± 0. 60 x 106 bacteria/ml

The key is in the INTERPRETATION p 96% confidence interval for the p 70% confidence interval for the true density, z* = 2. 054, and write true density, z* = 1. 036, and write = 28 ± 2. 054(1/√ 3) = 28 ± 1. 036(1/√ 3) = 28 ± 1. 19 x 106 bacteria/ml = 28 ± 0. 60 x 106 bacteria/ml For the first example, you can say: Based on this sample, I am 96% sure that the number of bacteria in the population is within 28 ± 1. 19 x 106 In the second example, you can say: Based on this sample, I am 70% sure that the number of bacteria in the population is within 28 ± 1. 06 x 106 Why do we have to specify the confidence level? (“I am 70 vs 96% sure”) Because it is possible that the particular sample we chose is one of the ones that fell outside of the range. Ie: Our particular sample just happened to yield an unusually high or low value. Remember that every sample is different!

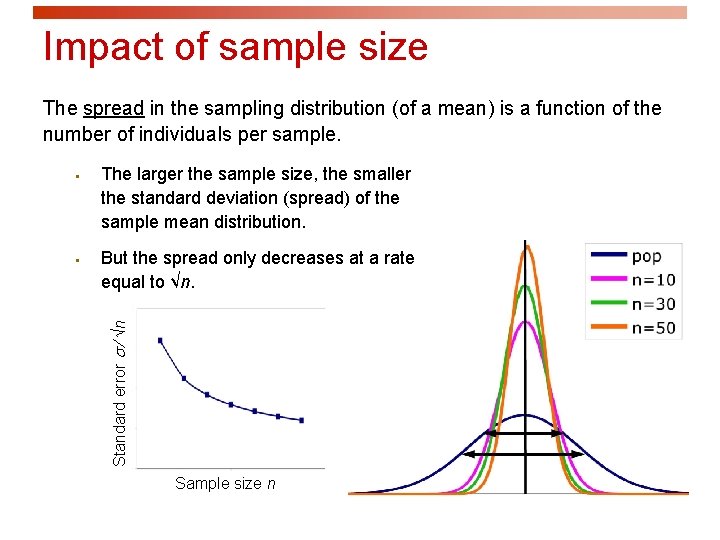
Impact of sample size The spread in the sampling distribution (of a mean) is a function of the number of individuals per sample. § The larger the sample size, the smaller the standard deviation (spread) of the sample mean distribution. But the spread only decreases at a rate equal to √n. Standard error ⁄ √n § Sample size n

** Example: Sample size and experimental design Sometimes you may need a specific margin of error (e. g. , drug trial, manufacturing specs). Typically, the population variability ( ) is difficult to change, however, but we can choose the number of measurements (n). So plan ahead what sample size to use to achieve that margin of error. Remember, though, that sample size is not always stretchable at will. There are typically costs and constraints associated with large samples. The best approach is to use the smallest sample size that can give you useful results.

What sample size for a given margin of error? Density of bacteria in solution: Measurement equipment has standard deviation σ = 1 * 106 bacteria/ml fluid. How many measurements should you make to obtain a margin of error of at most 0. 5 * 106 bacteria/ml with a confidence level of 90%? For a 90% confidence interval, z* = 1. 645. Using only 10 measurements will not be enough to ensure that m is no more than 0. 5 * 106. Therefore, we need at least 11 measurements.

Introduction to Inference Tests of Significance IPS Chapter 6. 2 © 2009 W. H. Freeman and Company

Objectives (IPS Chapter 6. 2) Tests of significance p The reasoning of significance tests p Stating hypotheses p The P-value p Statistical significance p Tests for a population mean p Confidence intervals to test hypotheses

For your exam: p Concepts: p p Hypothesis test § Null vs Alternative hypothesis § Rejecting vs Not Rejecting the null hypothesis p Statistical significance p P-value p One-tail vs two-tail p Significance Level α Calculations: p P-value for both one-sided and two-sided t tests.

Reasoning of Significance Tests Recall: sample mean We have seen that the properties of the sampling distribution of help us estimate a range of likely values for population mean . We can also rely on the properties of the sample distribution to test a theory (coming up). Example: You are in charge of quality control in your food company. You sample randomly four packs of whole cherry tomatoes, each pack labeled 1/2 lb. (227 g). The average weight from your four boxes is 222 g. Obviously, we cannot expect boxes filled with whole tomatoes to all weigh exactly half a pound. Thus, p p Is the somewhat smaller weight simply due to chance variation? Is our test evidence that the calibrating machine that sorts cherry tomatoes into packs needs calibration?

“Statistically Significant” Example: You are in charge of quality control in your food company. You sample randomly four packs of cherry tomatoes, each labeled 1/2 lb. (227 g). The average weight from your four boxes is 222 g. Oh NO!!!! Are we going to get sued for misleading our customers? Do we have to go back and recalibrate all of the machines in our factories? Probably not… Any thoughts on why we shouldn’t panic based on this test? Answer: Our sample size is quite small. In statistical jargon, we say that this test is “not statistically significant”.

** Use of a Hypothesis Test p In order to decide if a result is statistically significant, we must apply a hypothesis test. Be comfortable with these terms!!

Stating hypotheses A test of statistical significance tests a specific hypothesis (theory) using sample data. In statistics, a hypothesis is an assumption or theory about the characteristics of one or more variables in one or more populations. What you want to know: Does the calibrating machine that sorts cherry tomatoes into packs need revision? What we are REALLY trying to ask is: Does our sample give us a pretty good estimate of the population? ** So, the same question reframed statistically: “Is the population mean for the distribution of weights of cherry tomato packages equal to 227 g? ” (227 g = half a pound)

Important Terminology The null hypothesis is a (very) specific statement about some parameter of the population. It is labeled H 0. The alternative hypothesis is a statement about the same parameter of the population that is exclusive of the null hypothesis. It is labeled Ha. Weight of cherry tomato packs: H 0 : µ = 227 g (µ is the average weight of the population of packs) Ha : µ ≠ 227 g (µ is either larger or smaller than 227 g)

** “Rejecting the Null Hypothesis” p It is up to us to decide on the null hypothesis. p Typically though, the null hypothesis is the status-quo. That is, typically: p p We accept the previous claim or assumption to be true. Example: The cigarette manufacturer claims that it’s nicotine levels are no higher than 1. 4. § p If you have reason to believe that the nicotine values are actually higher, you would take a sample of cigarettes and look for nicotine levels higher than 1. 4 § p Ho : nicotine <= 1. 4 Ha: nicotine > 1. 4 “Rejecting the null hypothesis”: p If your sample shows that the nicotine levels are indeed > 1. 4, you can “reject the null hypothesis”. § p Typically, we are trying to reject the null hypothesis. If your sample does NOT fail to prove this result, then you “fail to reject the null hypothesis”.

* One-sided and two-sided tests p A two-tail or two-sided test of the population mean has these null and alternative hypotheses: H 0 : µ = [a specific number] Ha : µ [a specific number] p A one-tail or one-sided test of a population mean has these null and alternative hypotheses: H 0 : µ = [a specific number] Ha : µ < [a specific number] H 0 : µ = [a specific number] Ha : µ > [a specific number] OR The FDA tests whether a generic drug is absorbed by the body at a rate that is similar to the absorption of the brand-name drug. Higher or lower absorption would both be problematic, thus we would use a TWO-tailed test: H 0 : µgeneric = µbrand Ha : µgeneric µbrand (two-sided)

One or Two-tailed? Decide BEFORE! What determines the choice of a one-sided versus a two-sided test is what we know about the problem before we perform a test of statistical significance. A health advocacy group tests whether the mean nicotine content of a brand of cigarettes is greater than the advertised value of 1. 4 mg. One or two-tailed? Here, the health advocacy group suspects that a cigarette manufacturer is selling cigarettes with a nicotine content higher than what they advertise in order to better addict consumers to their products and maintain revenues. Thus, this is a one-sided test: H 0 : µ = 1. 4 mg Ha : µ > 1. 4 mg It is important to make that choice before performing the test or else you could make a choice of “convenience” or fall into circular logic.

*** Recap p So we wish to determine whether or not the results from our sample of 4 packages is statistically significant. In other words, does this sample give a relatively trustworthy picture of our population? p How do we determine if a result is statistically signficant? Answer: We apply a hypothesis test. p The numerical result calculated from a hypothesis test is called the P -value. p If the P-value is lower than a (pre-decided) significance level called alpha, we reject the null hypothesis (and accept our alternate hypothesis). p If the P-value is NOT lower than alpha, we fail to reject the nullhypothesis. In other words, we say that this sample has not convinced us to change our minds.

Overview of P-value p Recall that the P-value is the calculated result of a hypothesis test. p The smaller this P-value, the more confident we are that our sample accurately reflects the population. p In other words, if the P-value is small enough, we can say that our result is statistically significant. p A P-value that is too high (i. e. the result is not statistically significant) is one of the MOST COMMON ways in which people lie with statistics.

Significance Test and P-Value Restated: p “The spirit of a test of significance is to give a clear statement of the degree of evidence provided by the sample against the null hypothesis. ” p Represented by the P-value p As P gets lower, the evidence against the null hypothesis gets stronger. p Remember, we are typically trying to reject the null hypothesis!

Remember: All samples are different! The P-value Can we trust our sample? The packaging process has a known standard deviation = 5 g. H 0 : µ = 227 g versus Ha : µ ≠ 227 g The average weight from your sample of four random boxes is 222 g. Assuming H 0 is true, what is the probability of drawing a random sample just like this one? Tests of statistical significance quantify the chance of obtaining a particular random sample result if the null hypothesis were true. This quantity is called the P-value.

Interpreting a P-value The key point: Could variation in our samples account for the difference between the null hypothesis and the sample results? p A small P-value implies that random variation due to the sampling process is not likely to account for the observed difference. p With a small p-value we reject H 0. The true property of the population is “significantly” different from what was stated in H 0.

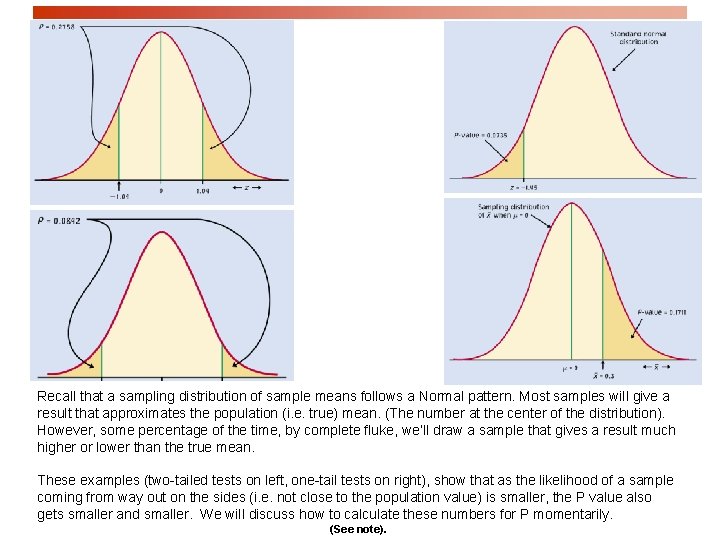
Recall that a sampling distribution of sample means follows a Normal pattern. Most samples will give a result that approximates the population (i. e. true) mean. (The number at the center of the distribution). However, some percentage of the time, by complete fluke, we’ll draw a sample that gives a result much higher or lower than the true mean. These examples (two-tailed tests on left, one-tail tests on right), show that as the likelihood of a sample coming from way out on the sides (i. e. not close to the population value) is smaller, the P value also gets smaller and smaller. We will discuss how to calculate these numbers for P momentarily. (See note).

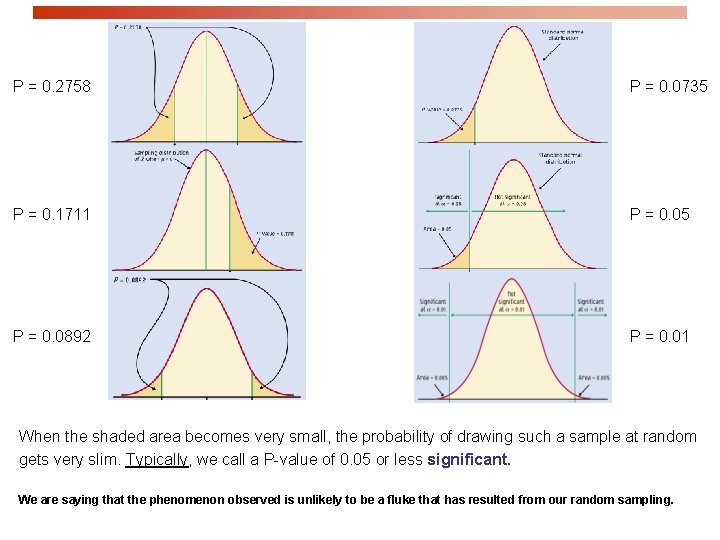
P = 0. 2758 P = 0. 0735 P = 0. 1711 P = 0. 05 P = 0. 0892 P = 0. 01 When the shaded area becomes very small, the probability of drawing such a sample at random gets very slim. Typically, we call a P-value of 0. 05 or less significant. We are saying that the phenomenon observed is unlikely to be a fluke that has resulted from our random sampling.

* Tests for a population mean To test the hypothesis H 0 : µ = µ 0 based on an SRS of size n from a Normal population with unknown mean µ and known standard deviation σ, we rely on the properties of the sampling distribution N(µ, σ/√n). The P-value is the area under the sampling distribution for values at least as extreme, (in the direction of Ha), as that of our random sample. It is a probability. If we are hoping to reject the null hypothesis, we want this value to be small. We begin by calculating a z-value: estimate – hypothesized value SD of the estimate I realize this slide is confusing. You will probably need to come back to it a few times.

P-value in one-sided and two-sided tests (null hypothesis value) One-sided (onetailed) test Two-sided (two -tailed) test To calculate the P-value for a two-sided test, use the symmetry of the normal curve. Find the P-value for a one-sided test and double it.

* Simplified (perhaps oversimplified) If your H refers to ‘<‘, then you calculate the probability to the left of p a your calculated z-score. p If your Ha refers to ‘>‘, then you calculate the probability to the right of your calculated z-score. p If your Ha refers to ‘not equal‘, then you add the two probabilities (to the right and left of your z-score). p Much faster: Calculate either one of the probabilities, and simpley double it!

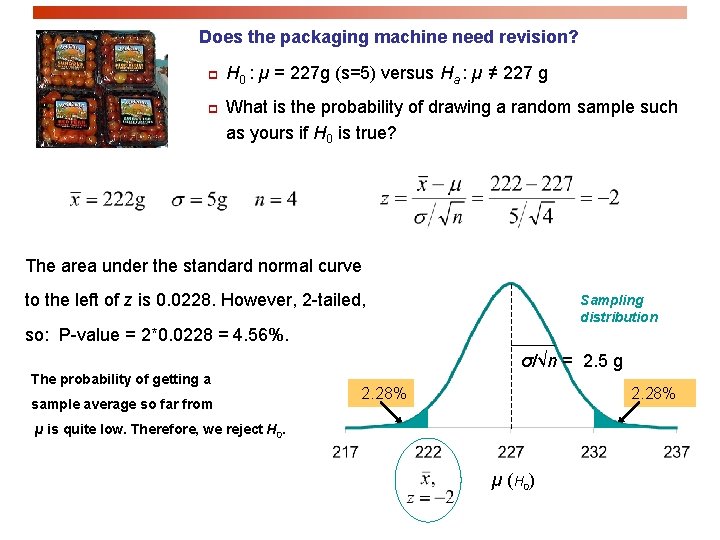
Does the packaging machine need revision? p p H 0 : µ = 227 g (s=5) versus Ha : µ ≠ 227 g What is the probability of drawing a random sample such as yours if H 0 is true? The area under the standard normal curve to the left of z is 0. 0228. However, 2 -tailed, Sampling distribution so: P-value = 2*0. 0228 = 4. 56%. σ/√n = 2. 5 g The probability of getting a sample average so far from 2. 28% µ is quite low. Therefore, we reject H 0. µ (H 0)

Interpreting a P-value So, small P-values are strong evidence against H 0. But just how small must the P-value be if we are to reject Ho? ? ?

The significance level ‘a ‘ The significance level is a very similar idea to the Confidence Level, C. Recall that we choose a confidence level, typically 95% as a “comfortable” level of confidence. But it is up to us to choose. We also understand that there is a tradeoff: The higher the C, we’ll be more confident, but at the price of a higher margin of error. Things work similarly, for statistical significance. The main difference is that we want a lower value for α. As with C, it’s up to us to decide what value of α we are “comfortable” with. Typically, we choose 5%. Allowing a lower α is more forgiving, but just as with desiring a higher C, there is a cost…

The significance level a The significance level, α, is the largest P-value tolerated for rejecting a true null hypothesis! This value is decided arbitrarily before conducting the test. p If the P-value is equal to or less than α (P ≤ α), then we reject H 0. p If the P-value is greater than α (P > α), then we fail to reject H 0. Does the packaging machine need revision? Two-sided test. The P-value is 4. 56%. * If α had been set to 5%, then the P-value would be significant. * If α had been set to 1%, then the P-value would not be significant.

Cautions about significance tests Choosing the significance level α Factors often considered: p p What are the consequences of rejecting the null hypothesis (e. g. , global warming, convicting a person for life with DNA evidence)? Are you conducting a preliminary study? If so, you may want a larger α so that you will be less likely to miss an interesting result. Some conventions: p We typically use the standards of our field of work. p There are no “sharp” cutoffs: e. g. , 4. 9% versus 5. 1 %. p It is the order of magnitude of the P-value that matters: “somewhat significant, ” “significant, ” or “very significant. ”

** One warning: p A lack of significance (P > alpha) does NOT necessarily mean that the null hypothesis is true. It just means that the evidence from our particular sample was not compelling enough to overturn our original belief.

Example (6. 15, p. 371) p A 1999 study looked at a large sample of university students and reported that the mean cholesterol level among women is 168 mg/dl with a standard deviation of 27 mg/dl. A much more recent study of 71 individuals found a mean level of 173. 7 mg/dl. Has the level changed in the intervening years? p p Note: We did NOT ask if the level increased, we simply are trying to establish whether the differences in the origianl data, differs from our more recent data. Solution: p p The ‘new’ data is from our sample: 173. 7. Our original data is 168. Ho = 168, Ha = 173. 7. sd = we will make the unrealistic assumption that it is the same as our original population data of 27. (I will make this clear on a test). p z = Est – Hyp / sd estimate p = (173. 7 – 168) / 27/ sqrt(71) p = 1. 78 p Now this is a positive z-score, and the probability of getting a value >1. 78 is 0. 0375. p However, because this would only be the ‘>’ situation, we also need to add the ‘<‘ situation. So we could add the probability of Z < -1. 78 (which is also 0. 0375). p Our P value is, therefore 0. 075 (or 7. 5%). This does not meet our typicaly 5% threshold, so we “fail to reject the null hypothesis”.

Example 6. 16, p. 372 p In a discussion of the average SATM (math SAT) scores of California HS students, an educational expert points out that because only those HS students planning on attending college will take this test, there is in fact, a selection bias at work. The person claims that if if all California HS students were to take the test, the score would be no higher than 450. As an experiment, a random sample of 500 students were given the test and scored 461. Is our expert’s claim borne out? p Answer: Ho: mu <= 450, Ha: mu > 450, sd = 100. p Note that because our Ha claim is of the ‘>’ type, we have a one-sided test. p Z = (461 -450) / (100/sqrt(500)) = 2. 46. p A z>2. 46 has a probability of 0. 00069. This is well below our threshold of 0. 05 and therefore we can reject Ho (our expert’s claim) that the average of all students would be below 450.


Practical significance – the number is not so important Statistical significance only says whether the effect observed is likely to be due to chance alone because of random sampling. Statistical significance may not be practically important. That’s because statistical significance doesn’t tell you about the magnitude of the effect, only that there is or isn’t one.

* Don’t ignore lack of significance p There is a tendency to conclude that there is no effect whenever a Pvalue fails to attain the alpha standard (e. g. 5%). p Consider this provocative title from the British Medical Journal: “Absence of evidence is not evidence of absence”. p Having no proof of who committed a murder does not imply that the murder was not committed. Indeed, failing to find statistical significance is not rejecting the null hypothesis. This is very different from actually accepting it. The sample size, for instance, could be too small to overcome large variability in the population.

Interpreting effect size: It’s all about context There is no consensus on how big an effect has to be in order to be considered meaningful. In some cases, effects that may appear to be trivial can be very important. p Example: Improving the format of a computerized test reduces the average response time by about 2 seconds. Although this effect is small, it is important since this is done millions of times a year. The cumulative time savings of using the better format is gigantic. Always think about the context. Try to plot your results, and compare them with a baseline or results from similar studies.

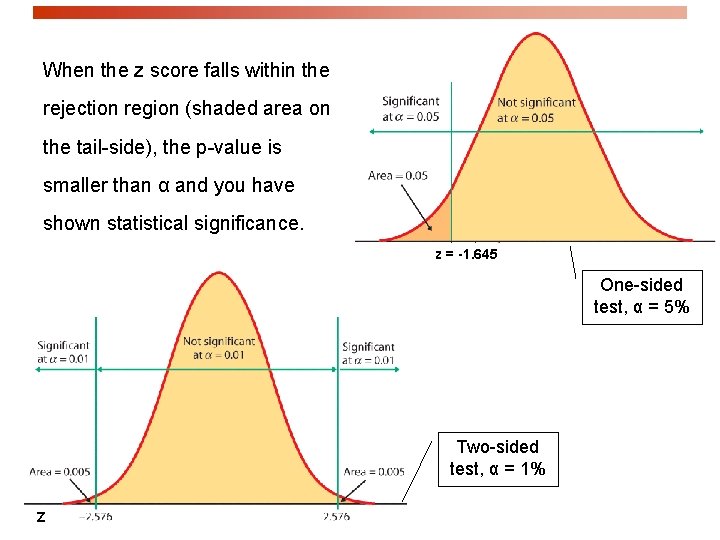
When the z score falls within the rejection region (shaded area on the tail-side), the p-value is smaller than α and you have shown statistical significance. z = -1. 645 One-sided test, α = 5% Two-sided test, α = 1% Z

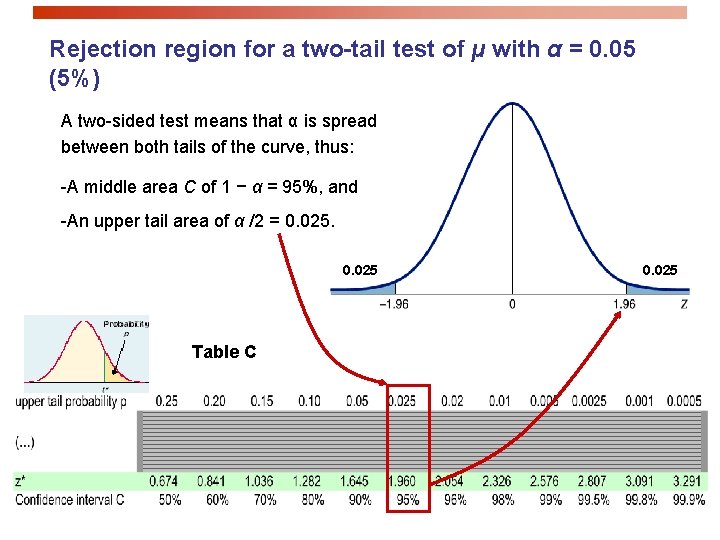
Rejection region for a two-tail test of µ with α = 0. 05 (5%) A two-sided test means that α is spread between both tails of the curve, thus: -A middle area C of 1 − α = 95%, and -An upper tail area of α /2 = 0. 025 Table C 0. 025

(Confidence intervals to test hypotheses) Because a two-sided test is symmetrical, you can also use a confidence interval to test a two-sided hypothesis. In a two-sided test, C = 1 – α. C confidence level α significance level α /2 Packs of cherry tomatoes (σ = 5 g): H 0 : µ = 227 g versus Ha : µ ≠ 227 g Sample average 222 g. 95% CI for µ = 222 ± 1. 96*5/√ 4 = 222 g ± 4. 9 g 227 g does not belong to the 95% CI (217. 1 to 226. 9 g). Thus, we reject H 0.

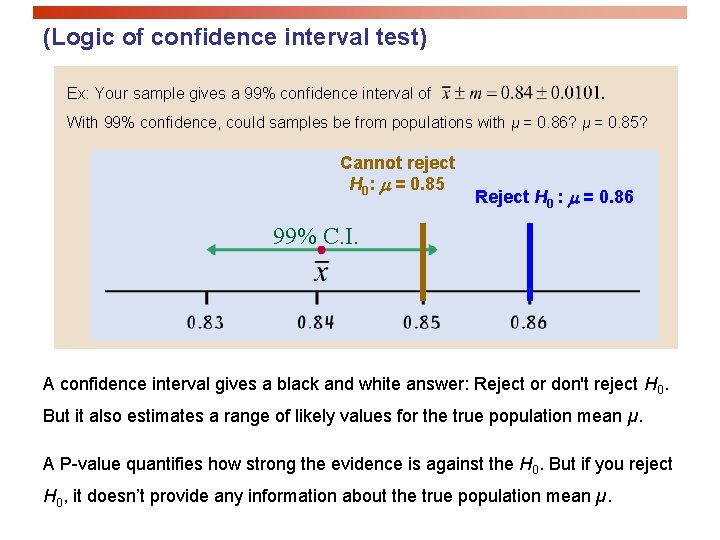
(Logic of confidence interval test) Ex: Your sample gives a 99% confidence interval of . With 99% confidence, could samples be from populations with µ = 0. 86? µ = 0. 85? Cannot reject H 0: m = 0. 85 Reject H 0 : m = 0. 86 99% C. I. A confidence interval gives a black and white answer: Reject or don't reject H 0. But it also estimates a range of likely values for the true population mean µ. A P-value quantifies how strong the evidence is against the H 0. But if you reject H 0, it doesn’t provide any information about the true population mean µ.

Introduction to Inference Use and Abuse of Tests; Power and Decision IPS Chapters 6. 3 and 6. 4 © 2009 W. H. Freeman and Company

Objectives (IPS Chapters 6. 3 and 6. 4) Use and abuse of tests Power and inference as a decision p Cautions about significance tests p Power of a test p Type I and II errors p Error probabilities

The power of a test of hypothesis with fixed significance level α is the probability that the test will reject the null hypothesis when the alternative is true. In other words, power is the probability that the data gathered in an experiment will be sufficient to reject a wrong null hypothesis. Knowing the power of your test is important: p When designing your experiment: select a sample size large enough to detect an effect of a magnitude you think is meaningful. p When a test found no significance: Check that your test would have had enough power to detect an effect of a magnitude you think is meaningful.

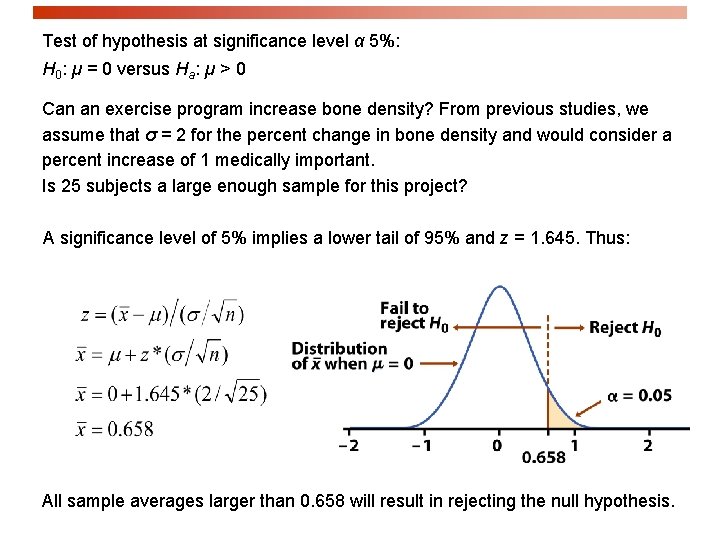
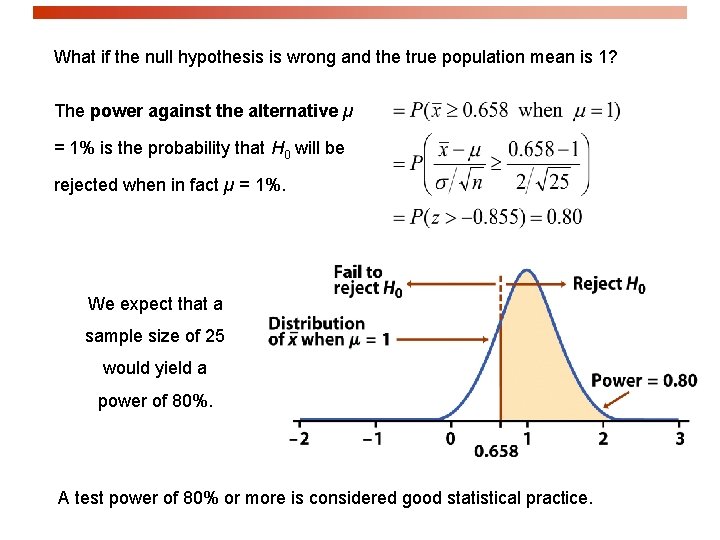
Test of hypothesis at significance level α 5%: H 0: µ = 0 versus Ha: µ > 0 Can an exercise program increase bone density? From previous studies, we assume that σ = 2 for the percent change in bone density and would consider a percent increase of 1 medically important. Is 25 subjects a large enough sample for this project? A significance level of 5% implies a lower tail of 95% and z = 1. 645. Thus: All sample averages larger than 0. 658 will result in rejecting the null hypothesis.

What if the null hypothesis is wrong and the true population mean is 1? The power against the alternative µ = 1% is the probability that H 0 will be rejected when in fact µ = 1%. We expect that a sample size of 25 would yield a power of 80%. A test power of 80% or more is considered good statistical practice.

Factors affecting power: Size of the effect The size of the effect is an important factor in determining power. Larger effects are easier to detect. More conservative significance levels (lower α) yield lower power. Thus, using an α of. 01 will result in less power than using an α of. 05. Increasing the sample size decreases the spread of the sampling distribution and therefore increases power. But there is a tradeoff between gain in power and the time and cost of testing a larger sample. A larger variance σ2 implies a larger spread of the sampling distribution, σ/sqrt(N). Thus, the larger the variance, the lower the power. The variance is in part a property of the population, but it is possible to reduce it to some extent by carefully designing your study.

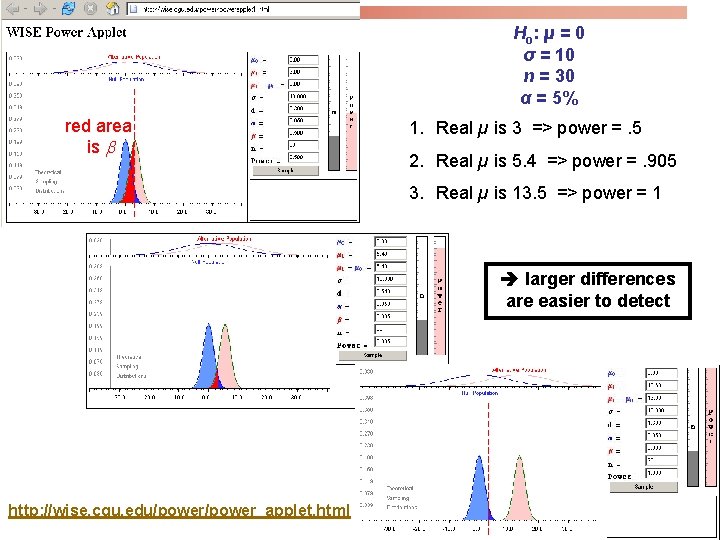
Ho: µ = 0 σ = 10 n = 30 α = 5% red area is 1. Real µ is 3 => power =. 5 2. Real µ is 5. 4 => power =. 905 3. Real µ is 13. 5 => power = 1 larger differences are easier to detect http: //wise. cgu. edu/power_applet. html

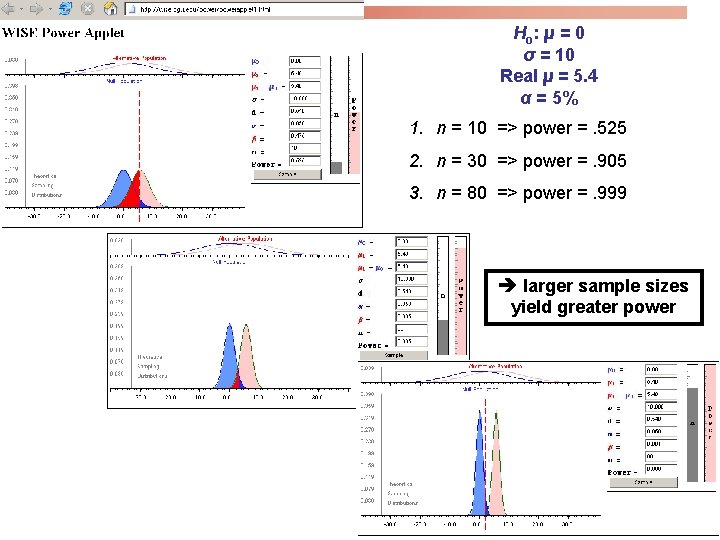
Ho: µ = 0 σ = 10 Real µ = 5. 4 α = 5% 1. n = 10 => power =. 525 2. n = 30 => power =. 905 3. n = 80 => power =. 999 larger sample sizes yield greater power

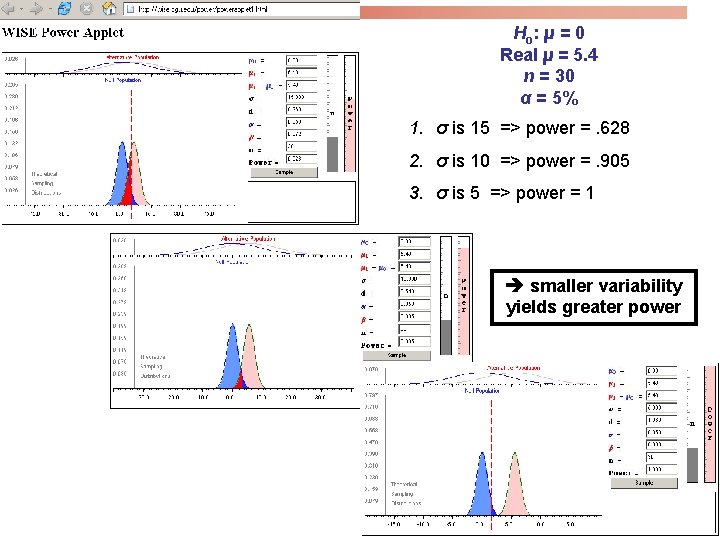
Ho: µ = 0 Real µ = 5. 4 n = 30 α = 5% 1. σ is 15 => power =. 628 2. σ is 10 => power =. 905 3. σ is 5 => power = 1 smaller variability yields greater power

Type I and II errors p A Type I error is made when we reject the null hypothesis and the null hypothesis is actually true (incorrectly reject a true H 0). The probability of making a Type I error is the significance level p A Type II error is made when we fail to reject the null hypothesis and the null hypothesis is false (incorrectly keep a false H 0). The probability of making a Type II error is labeled . The power of a test is 1 − .

Running a test of significance is a balancing act between the chance α of making a Type I error and the chance of making a Type II error. Reducing α reduces the power of a test and thus increases . It might be tempting to emphasize greater power (the more the better). p However, with “too much power” trivial effects become highly significant. p A type II error is not definitive since a failure to reject the null hypothesis does not imply that the null hypothesis is wrong.

Example: p Recall our egg-size example. Suppose our sample gave the result of 64 g and an sd of 1. 44. p If we choose a confidence level (C) of 95%, this means we are saying that we are 95% sure the range 64 +/- 2 sd contains the population value. p If we choose a confidence level of 99%, then we can say that we are 99% sure that the range 64 +/- INCOMPLETE…
 Chapter 8 estimating with confidence
Chapter 8 estimating with confidence Chapter 8 estimating with confidence
Chapter 8 estimating with confidence Chapter 8 estimating with confidence
Chapter 8 estimating with confidence Confidence interval vs confidence level
Confidence interval vs confidence level Critical value for z score
Critical value for z score Chapter 19 confidence intervals for proportions
Chapter 19 confidence intervals for proportions Chapter 18 confidence intervals for proportions
Chapter 18 confidence intervals for proportions Chapter 19 confidence intervals for proportions
Chapter 19 confidence intervals for proportions Chapter 2 building confidence
Chapter 2 building confidence Confidence interval for variance
Confidence interval for variance Biologists wish to cross pairs of tobacco plants
Biologists wish to cross pairs of tobacco plants Chapter 12 inference for proportions answers
Chapter 12 inference for proportions answers Chapter 11 inference for distributions of categorical data
Chapter 11 inference for distributions of categorical data Chapter 11 inference for distributions of categorical data
Chapter 11 inference for distributions of categorical data Types of tps system
Types of tps system Front-end rounding
Front-end rounding Mcaces
Mcaces Estimating the degradation function
Estimating the degradation function Gao cost estimating guide
Gao cost estimating guide Estimating with decimals
Estimating with decimals Tendering and estimating
Tendering and estimating Shruti sheladia
Shruti sheladia Dr.nabil 300 k
Dr.nabil 300 k Absolute volume formula
Absolute volume formula Estimating avogadro's number lab
Estimating avogadro's number lab Electrical wiring estimating and costing
Electrical wiring estimating and costing Cost analysis and estimating for engineering and management
Cost analysis and estimating for engineering and management Common critical values
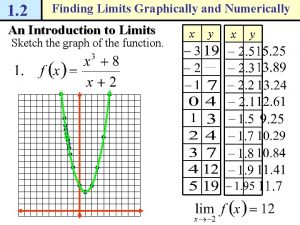
Common critical values 12-1 estimating limits graphically
12-1 estimating limits graphically Agile estimating and planning by mike cohn
Agile estimating and planning by mike cohn Calculating time of death worksheet
Calculating time of death worksheet Estimating with percents
Estimating with percents Estimating limit values from tables
Estimating limit values from tables Estimating limits numerically
Estimating limits numerically Estimating whole numbers
Estimating whole numbers Hurdle principle
Hurdle principle Clustering estimation with decimals
Clustering estimation with decimals Bluebeam estimating tools
Bluebeam estimating tools Estimating the difference between two means
Estimating the difference between two means Approximating square roots to the nearest hundredth
Approximating square roots to the nearest hundredth Estimating products of fractions
Estimating products of fractions Estimating sums and differences of fractions
Estimating sums and differences of fractions Example of a proportion
Example of a proportion Ccwfel
Ccwfel Estimating square roots word problems
Estimating square roots word problems Cooling load software
Cooling load software Square root notes
Square root notes Cost analysis and estimating for engineering and management
Cost analysis and estimating for engineering and management Cost analysis and estimating for engineering and management
Cost analysis and estimating for engineering and management Voyage estimating decision support system
Voyage estimating decision support system Estimating percents
Estimating percents Billick brothers is estimating its wacc
Billick brothers is estimating its wacc 567x7
567x7 Estimating project time and cost
Estimating project time and cost Normal vs expedited costs
Normal vs expedited costs Cost analysis and estimating for engineering and management
Cost analysis and estimating for engineering and management Estimating project time and cost
Estimating project time and cost Voyage estimating decision support system
Voyage estimating decision support system Activity duration estimating
Activity duration estimating Parametric estimating
Parametric estimating Estimating soil moisture by feel and appearance
Estimating soil moisture by feel and appearance Estimating human shape and pose from a single image
Estimating human shape and pose from a single image Essentials of management information systems
Essentials of management information systems Types of information systems
Types of information systems All perfect square numbers
All perfect square numbers Place value and estimating
Place value and estimating Estimating sums and differences of whole numbers
Estimating sums and differences of whole numbers Bottom up estimating
Bottom up estimating Mining estimating software
Mining estimating software Cost analysis and estimating for engineering and management
Cost analysis and estimating for engineering and management Sejarah perkembangan ips
Sejarah perkembangan ips Keterkaitan pkn dan ips
Keterkaitan pkn dan ips Standar kompetensi dan kompetensi dasar mata pelajaran ips
Standar kompetensi dan kompetensi dasar mata pelajaran ips Materi ips kelas 6 sd tentang asean
Materi ips kelas 6 sd tentang asean Sexual harrasment prevention training
Sexual harrasment prevention training Sejarah singkat perkembangan ips di indonesia
Sejarah singkat perkembangan ips di indonesia Rangkuman materi esensial
Rangkuman materi esensial Kamal kumar ips
Kamal kumar ips