Introduction to High Speed Airbreathing Propulsion Systems MAE

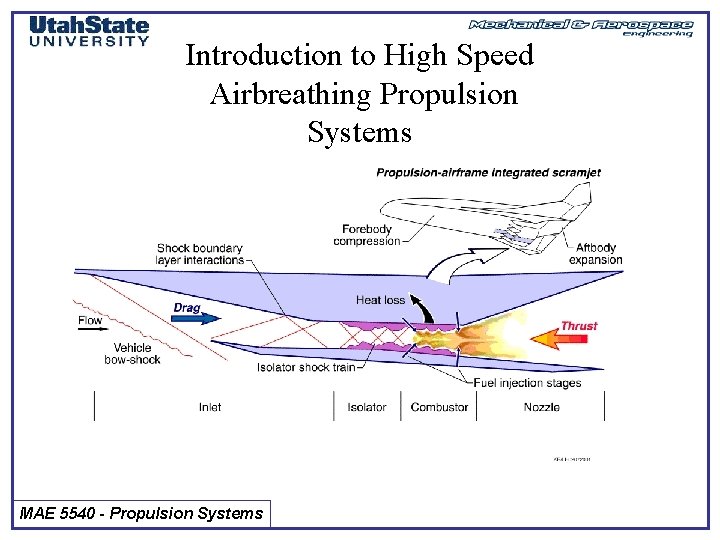
Introduction to High Speed Airbreathing Propulsion Systems MAE 5540 - Propulsion Systems

• Oxidizer … “liquid air” Have to take our own along So that the engine can breathe At high altitudes • How Much Oxidizer? … depending op chosen propellants … 4 -9 times as much As the fuel we carry! MAE 5540 - Propulsion Systems

Flight Without Oxidizer, I What if we could get enough oxygen from ambient air? X-43 airbreathing SCRAMjet engine What happens to our Isp? OK. . Lets loose the Oxidizer … and our Isp goes up by a factor Of 7! … but where do we the Oxidizer for combustion? …. MAE 5540 - Propulsion Systems

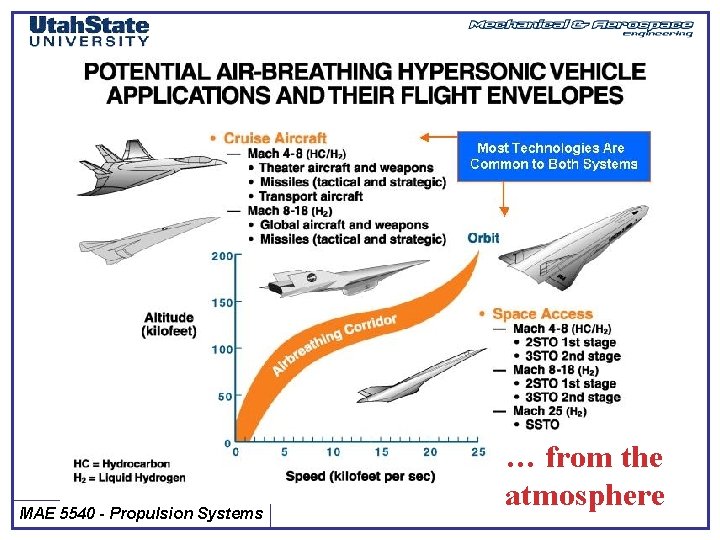
MAE 5540 - Propulsion Systems … from the atmosphere

Flight Without Oxidizer, II Do Not Need Oxidizer here For a large portion of the Launch trajectory there is Plenty Enough air For combustion if you are going fast enough Need Oxidizer here MAE 5540 - Propulsion Systems

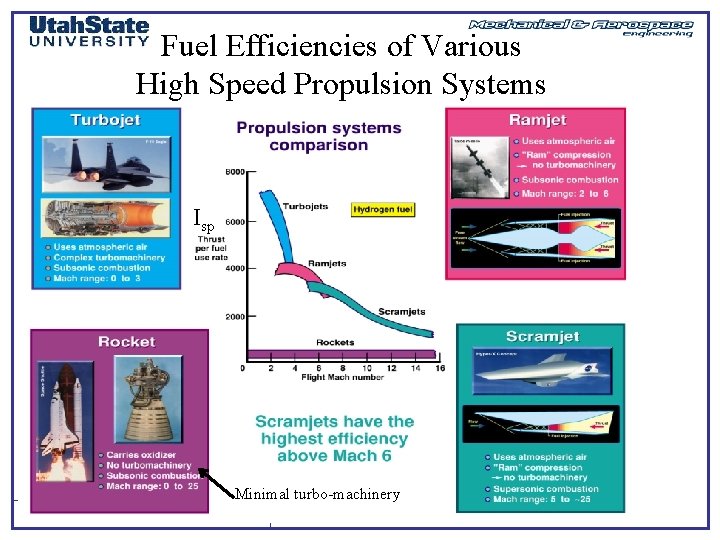
Fuel Efficiencies of Various High Speed Propulsion Systems Isp Minimal turbo-machinery MAE 5540 - Propulsion Systems

Operational Flight Envelope for Various Flight Vehicles MAE 5540 - Propulsion Systems

Operations Payoffs for Airbreathing Launch • Decreased gross lift-off weight, resulting in smaller facilities and easier handling • Wider range of emergency landing sites for intact abort • Powered flyback/go-around & more margin at reduced power • Self-ferry & taxi capabilities • Greatly expanded launch windows (double or triple) • Rapid orbital rendezvous (up to three times faster than rockets) • Wider array of landing sites from orbit, with 2, 000 -mile cross range and increased range • Reduced sensitivity to weight growth MAE 5540 - Propulsion Systems

Applications MAE 5540 - Propulsion Systems

Our total launch mass goes from 10, 000 kg/kg down to <1400 kg/kg wow! MAE 5540 - Propulsion Systems

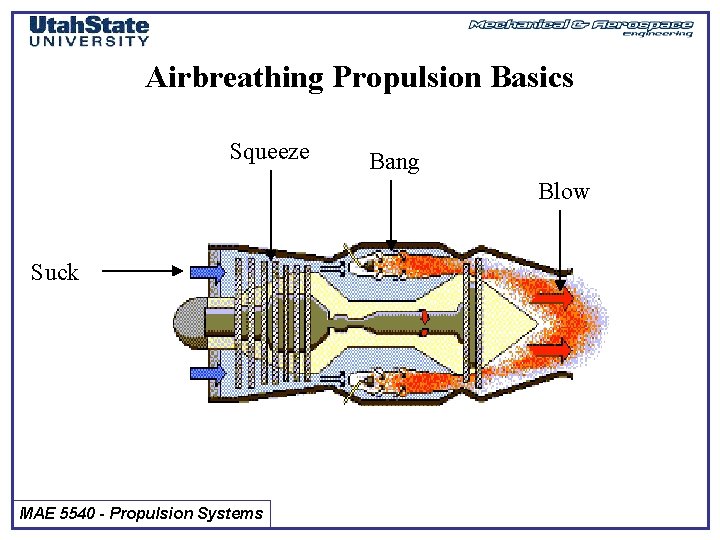
Airbreathing Propulsion Basics Squeeze Bang Blow Suck MAE 5540 - Propulsion Systems

Brayton Cycle for Airbreathing Combustion Step 1) Intake (suck) 2) 3) 4) 5) Compress the Air (squeeze) Add heat (bang) Extract work (blow) Exhaust … step 5 above happens In the exhaust plume and has minimal Effect on engine performance Process Isentropic Compression Adiabatic Compression Constant Pressure Combustion Isentropic Expansion in Nozzle Heat extraction by surroundings Step 3 Step 1 -2 Step 4 Step 5 MAE 5540 - Propulsion Systems (Credit Narayanan Komerath, Georgia Tech)

Brayton Cycle for Airbreathing Combustion (cont’d) • Ramjet Engine Combustion Cycle Steps (Credit Narayanan Komerath, Georgia Tech) Step 1 -2 Step 3 MAE 5540 - Propulsion Systems Step 4 • Compression and Power extraction steps Performed passively

Brayton Cycle for Airbreathing Combustion (cont’d) Turbine • Turbojet/Turbo fan engines Combustion Cycle steps Compression and Power extraction steps use Turbo-machinery To augment cycle Combustor Compressor Nozzle Turbojet Inlet Afterburner Turbine Compressor Afterburner Turbofan Inlet MAE 5540 - Propulsion Systems Fan Combustor Nozzle

Ideal Ramjet Cycle Analysis Step 1 -2 Step 3 Step 4 Region Process Ideal Behavior Real Behavior A to 1(inlet) Isentropic flow P 0, T 0 constant P 0 drop 1 -2 (diffuser) Adiabatic Compression P, T increase P 0 drop 2 -3 (burner) Heat Addition P 0 constant, T 0 s Increase P 0 drop T 0, P 0 constant s Increase T 0 drop 3 -4 (nozzle) Isentropic expansion MAE 5540 - Propulsion Systems

Ideal Ramjet Cycle Analysis T-s Diagram Step 1 -2 T s MAE 5540 - Propulsion Systems Step 3 Step 4

Thermodynamic Efficiency of Ideal Ramjet • Net Work Available --> work perform by system in step 4 minus work required for step 1 -2 • Net heat input --> heat input during step 3 (combustion) - heat lost in exhaust plume (Credit Narayanan Komerath, Georgia Tech) Step 1 -2 MAE 5540 - Propulsion Systems Step 3 Step 4

Thermodynamic Efficiency of Ideal Ramjet (cont’d) • Ideal Cycle Efficiency( ) = (Net work output)/(Net heat input} (Credit Narayanan Komerath, Georgia Tech) Step 1 -2 Step 3 Step 4 MAE 5540 - Propulsion Systems

Thermodynamic Efficiency of Ideal Ramjet (cont’d) • Ideal Cycle Efficiency = (Net work output)/(Net heat input} (Credit Narayanan Komerath, Georgia Tech) Step 1 -2 Step 3 Step 4 MAE 5540 - Propulsion Systems

Thermodynamic Efficiency of Ideal Ramjet (cont’d) • Assume … Cpair ~ Cpproducts (Credit Narayanan Komerath, Georgia Tech) Step 1 -2 Step 3 Step 4 MAE 5540 - Propulsion Systems

Thermodynamic Efficiency of Ideal Ramjet (cont’d) • For simplicity … let … Cpair ~ Cpproducts MAE 5540 - Propulsion Systems

Thermodynamic Efficiency of Ideal Ramjet (cont’d) • From C-->D flow is isentropic … (Credit Narayanan Komerath, Georgia Tech) Step 1 -2 MAE 5540 - Propulsion Systems Step 3 Step 4

Thermodynamic Efficiency of Ideal Ramjet (cont’d) • Adiabatic compression across diffuser (Credit Narayanan Komerath, Georgia Tech) Step 1 -2 MAE 5540 - Propulsion Systems Step 3 Step 4

Thermodynamic Efficiency of Ideal Ramjet (cont’d) • Sub into efficiency equation (Credit Narayanan Komerath, Georgia Tech) Step 1 -2 MAE 5540 - Propulsion Systems Step 3 Step 4

Thermodynamic Efficiency of Ideal Ramjet (cont’d) (Credit Narayanan Komerath, Georgia Tech) Step 1 -2 MAE 5540 - Propulsion Systems Step 3 Step 4

Thermodynamic Efficiency of Ideal Ramjet (cont’d) (Credit Narayanan Komerath, Georgia Tech) Step 1 -2 Step 3 Step 4 i) As engine pressure ratio, PB/PA, goes up … h goes up ii) As combustor temperature difference TC-TB iii) goes up … h goes up iv) iii) As inlet total pressure ratio (P 0 B/P 0 A) goes down … v) (stagnation pressure loss goes up) … h goes down vi) MAE 5540 - Propulsion Systems

Why is total pressure recovery important? • Choked Nozzle Throat massflow • Thrust is proportional to engine massflow MAE 5540 - Propulsion Systems

Ideal Ramjet: Inlet and Diffuser • Take a Rocket motor and “lop the top off” • Works Ok for subsonic, but for supersonic flow … can’t cram enough air down the tube • Result is a normal shock wave at the inlet lip MAE 5540 - Propulsion Systems

Ideal Ramjet: Inlet and Diffuser (cont’d) M M • Mechanical Energy is Dissipated into Heat • Huge Loss in Momentum MAE 5540 - Propulsion Systems

Ideal Ramjet: Inlet and Diffuser (cont’d) • So … we put a spike in front of the inlet • How does this spike Help? • By forming an Oblique Shock wave ahead of the inlet MAE 5540 - Propulsion Systems

Oblique Shockwave Theory Background • In Supersonic flow, pressure disturbances cannot outrun “point-mass” generating object • Result is an infinitesimally weak “mach wave” MAE 5540 - Propulsion Systems Anderson, Compressible Flow, Chapter 4 pp. 127 -145

Oblique Shock Wave (cont’d) • When generating object is larger than a “point”, shockwave is stronger than mach wave …. Oblique shock wave b>m q • b -- shock angle • q -- turning or “wedge angle” MAE 5540 - Propulsion Systems

Oblique Shock Wave Geometry • Must satisfy i) continuity ii) momentum iii) energy Ahead Of Shock Behind Shock MAE 5540 - Propulsion Systems Tangential w 1 , Mt 1 Normal u 1, Mn 1 w 2 , Mt 2 u 2, Mn 2

Collected Oblique Shock Equations • Continuity • Momentum • Energy MAE 5540 - Propulsion Systems

Oblique Shock Waves: Collected Algorithm • Properties across Oblique Shock wave ~ f(M 1, b) • q is the geometric angle that “forces” the flow MAE 5540 - Propulsion Systems

Oblique Shock Waves: Collected Algorithm (cont’d) • Can be re-written as third order polynomial in tan(q) • “Very Easy” numerical solution • Cubic equation has three solutions i) weak shock ii) Strong shock iii) non-physical solution MAE 5540 - Propulsion Systems

Oblique Shock Waves: Collected Algorithm (cont’d) • “Less Obvious” explicit solution = 0 ---> Strong Shock = 1 ---> Weak Shock MAE 5540 - Propulsion Systems

Oblique Shock Waves: Collected Algorithm (cont’d) • . . . and the rest of the story … MAE 5540 - Propulsion Systems

Oblique Shock Waves: Collected Algorithm (concluded) • . . . and the rest of the story … MAE 5540 - Propulsion Systems

Basic Oblique Shock Example: • M 1 = 3. 0, p 1=1 atm, T 1=288 K, q=20 =1. 4, • Compute shock wave angle (weak) • Compute P 02, T 02, p 2, T 2, M 2 … Behind Shockwave MAE 5540 - Propulsion Systems

Basic Oblique Shock Example : (cont’d) • M 1 = 3. 0, p 1=1 atm, =1. 4, T 1=288 K, q=20 • Explicit Solver for b =7. 13226 =0. 93825 MAE 5540 - Propulsion Systems

Basic Oblique Shock Example : (cont’d) • M 1 = 3. 0, p 1=1 atm, =1. 4, T 1=288 K, q=20 • = 1 (weak shock) = 37. 764 MAE 5540 - Propulsion Systems

Basic Oblique Shock Example : (cont’d) • M 1 = 3. 0, p 1=1 atm, =1. 4, T 1=288 K, q=20 • ������� Normal Component of Free stream mach Number =1. 837 • Compute Pressure ratio across shock Normal Shock Solver p 2 = 3. 771(1 atm) = 3. 771 atm MAE 5540 - Propulsion Systems • Flow is compressed

Basic Oblique Shock Example : (cont’d) • M 1 = 3. 0, p 1=1 atm, =1. 4, T 1=288 K, q=20 • ������� Temperature ratio Across Shock Normal Shock Solver T 2 = 1. 5596(288 K) = 449. 2 K MAE 5540 - Propulsion Systems

Basic Oblique Shock Example : (cont’d) • M 1 = 3. 0, p 1=1 atm, =1. 4, T 1=288 K, q=20 • ������� Stagnation Pressure ratio across shock =1. 837 Normal Shock Solver 0. 7961 MAE 5540 - Propulsion Systems

Basic Oblique Shock Example : (cont’d) • M 1 = 3. 0, p 1=1 atm, =1. 4, T 1=288 K, q=20 • ������� Stagnation Pressure ratio (alternate method) =0. 7961 MAE 5540 - Propulsion Systems

Basic Oblique Shock Example : (cont’d) • M 1 = 3. 0, p 1=1 atm, =1. 4, T 1=288 K, q=20 • ������� Stagnation Pressure =29. 24 atm MAE 5540 - Propulsion Systems

Basic Oblique Shock Example : (cont’d) • M 1 = 3. 0, p 1=1 atm, =1. 4, T 1=288 K, q=20 • ������� Stagnation Temperature behind shock MAE 5540 - Propulsion Systems =806. 4 o. K

2 -D Ramjet Inlet Example P 0 B M 1=4. 0 b= 40 B • Compare MB and P 0 behind normal shockwaves B MAE 5540 - Propulsion Systems P 0 B Assume =1. 4

2 -D Ramjet Inlet Example (cont’d) M 1=4. 0 P 0 B B • From Normal Shock wave solver MAE 5540 - Propulsion Systems

2 -D Ramjet Inlet Example (cont’d) b= 40 B • Across Oblique Shock wave • M 1 n= M 1 sin b 1 = MAE 5540 - Propulsion Systems =2. 571 q = 26. 2 M 2 n=0. 5064

2 -D Ramjet Inlet Example (cont’d) b= 40 B • Across Oblique Shock wave =2. 123 P 02/P 0 = 0. 4711 MAE 5540 - Propulsion Systems

2 -D Ramjet Inlet Example (cont’d) b= 40 B • Across Normal Shock wave (behind oblique Shock) = 38. 422 MAE 5540 - Propulsion Systems

2 -D Ramjet Inlet Example (cont’d) M 1=4. 0 • Compare • Spike aids in increasing Total Pressure recovery Reducing “ram drag” M 1=4. 0 MAE 5540 - Propulsion Systems

2 -D Ramjet Inlet Example (cont’d) • … Continuing example … Incoming Air to Ramjet • Molecular weight • • Rg • T • p • Combustor = = = � � 28. 96443 kg/kg-mole 1. 40 287. 056 J/ K-(kg) 216. 65 K 19. 330 k. Pa 500 k. J/kg • Assume that mass of added fuel is negligible, exhaust and g, Rg are the same MAE 5540 - Propulsion Systems

2 -D Ramjet Inlet Example (cont’d) • Compute free stream stagnation temperature =909. 93 K • Compute BURNER stagnation temperature = 1407. 6 K (Credit Narayanan Komerath, Georgia Tech) Step 1 -2 Step 3 Step 4 MAE 5540 - Propulsion Systems

2 -D Ramjet Inlet Example (cont’d) • Compute efficiency …. Normal shock inlet M 1=4. 0 • Compute TC, TB TC = = 867. 75 K TB = MAE 5540 - Propulsion Systems = 1356. 3 K

2 -D Ramjet Inlet Example (cont’d) • Compute efficiency …. Normal shock inlet M 1=4. 0 • Compute TC, TB TC = 867. 75 K = TB = 1356. 3 K =0. 2328 MAE 5540 - Propulsion Systems

2 -D Ramjet Inlet Example (cont’d) • Compute efficiency …. Oblique shock inlet M 1=4. 0 • Compute TC, TB TC = = 856. 61 K TB = MAE 5540 - Propulsion Systems = 1325. 1 K

2 -D Ramjet Inlet Example (cont’d) • Compute efficiency …. Oblique shock inlet M 1=4. 0 • Compute TC, TB TC = 856. 61 K = TB = 1325. 1 K = 0. 4652 MAE 5540 - Propulsion Systems

2 -D Ramjet Inlet Example (cont’d) • Compute efficiency …. Oblique shock inlet M 1=4. 0 = 0. 2328 = 0. 4652 M 1=4. 0 MAE 5540 - Propulsion Systems 200% increase in efficiency!

Supersonic Inlet: Condorde Inlet Design • Mach 2 Cruise MAE 5540 - Propulsion Systems Credit: http: //www. concordesst. com/powerplant. html

Conical versus 2 -D Inlets SR-71 Concorde X-15 MAE 5540 Ramjet - Propulsion Systems F-15

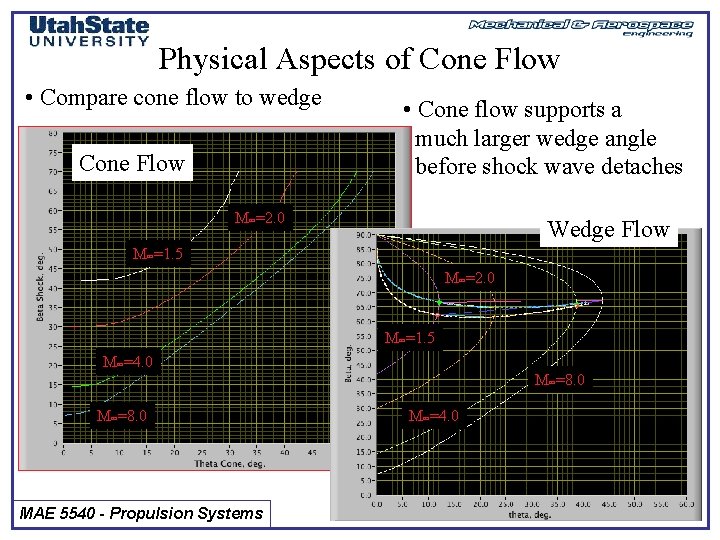
Physical Aspects of Cone Flow • Compare cone flow to wedge Cone Flow • Cone flow supports a much larger wedge angle before shock wave detaches M =2. 0 Wedge Flow M =1. 5 M =2. 0 M =1. 5 M =4. 0 M =8. 0 MAE 5540 - Propulsion Systems M =4. 0

Physical Aspects of Cone Flow (cont’d) • Three-dimensional “relieving” effect • Cone shock wave is Effectively weaker Than shock wave for Corresponding wedge angle • Conical Inlet not at effective as 2 -D inlet … but much less “draggy” MAE 5540 - Propulsion Systems

Air to Fuel Ratio Computations (Credit Narayanan Komerath, Georgia Tech) Step 1 -2 Step 3 Step 4 • Stagnation enthalpy of the air and burned products leaving the combustor equals the enthalpy of the air entering the combustor + heat released by chemical reaction • Sensible enthalpy of fuel assumed to be negligible when compared to heat of reaction MAE 5540 - Propulsion Systems

Fuel to Air Ratio Computations (cont’d) (Credit Narayanan Komerath, Georgia Tech) Step 1 -2 Step 3 Solve for f MAE 5540 - Propulsion Systems T 02 -- stagnation temperature entering burner T 03 -- stagnation temperature exiting burner f fuel to air ratio Step 4 -- Cp 2 -- specific heat of air entering burner Cp 3 -- specific heat of combustion products qr -- heat of reaction

Equivalence Ratio versus Mixture Ratio • The equivalence ratio is used to characterize the mixture ratio Of airbreathing engines … analogous to mixture ratio • The equivalence ratio, , is defined as the ratio of the actual fuel-air ratio to the stoichiometric fuel-air ratio. … > 1 ---> a rich mixture … < 1 ---> lean mixture • For F = 1, no oxygen is left in exhaust products … combustion is called stoichiometric MAE 5540 - Propulsion Systems

Equivalence Ratio versus Mixture Ratio (cont’d) • Consider combustion of H 2 fuel with air … what is Stoich fuel ratio (define only water as product of combustion) Air/Fuel=38. 09 • Assumed equilibrium chemistry is described by reaction above with only water vapor as combustion product, + left over atmospheric nitrogen MAE 5540 - Propulsion Systems

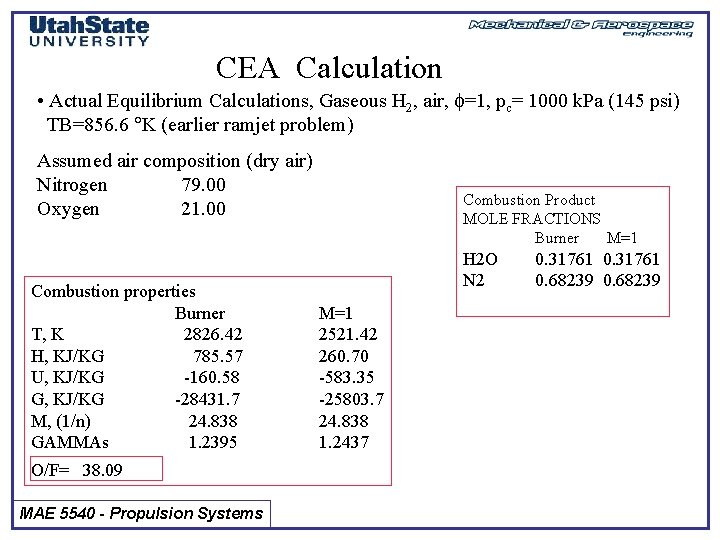
CEA Calculation • Actual Equilibrium Calculations, Gaseous H 2, air, f=1, pc= 1000 k. Pa (145 psi) TB=856. 6 K (earlier ramjet problem) Assumed air composition (dry air) Nitrogen 79. 00 Oxygen 21. 00 Combustion properties Burner T, K 2826. 42 H, KJ/KG 785. 57 U, KJ/KG -160. 58 G, KJ/KG -28431. 7 M, (1/n) 24. 838 GAMMAs 1. 2395 O/F= 38. 09 MAE 5540 - Propulsion Systems Combustion Product MOLE FRACTIONS Burner M=1 H 2 O N 2 M=1 2521. 42 260. 70 -583. 35 -25803. 7 24. 838 1. 2437 0. 31761 0. 68239

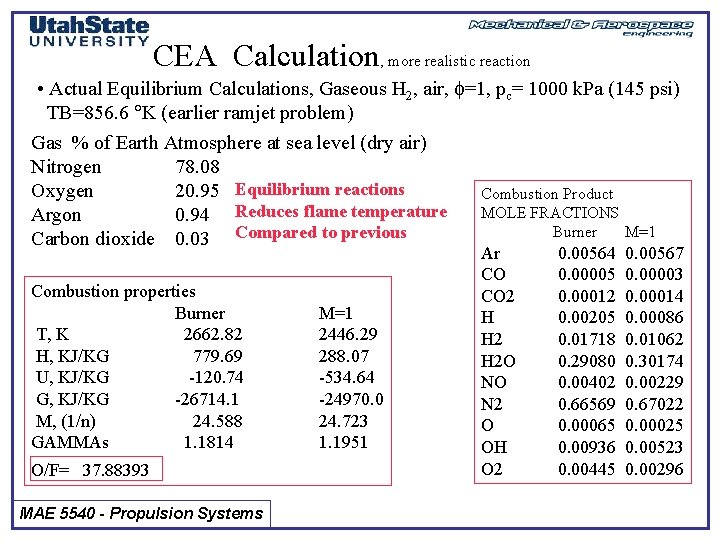
CEA Calculation, more realistic reaction • Actual Equilibrium Calculations, Gaseous H 2, air, f=1, pc= 1000 k. Pa (145 psi) TB=856. 6 K (earlier ramjet problem) Gas % of Earth Atmosphere at sea level (dry air) Nitrogen 78. 08 Oxygen 20. 95 Equilibrium reactions Argon 0. 94 Reduces flame temperature Carbon dioxide 0. 03 Compared to previous Combustion properties Burner T, K 2662. 82 H, KJ/KG 779. 69 U, KJ/KG -120. 74 G, KJ/KG -26714. 1 M, (1/n) 24. 588 GAMMAs 1. 1814 O/F= 37. 88393 MAE 5540 - Propulsion Systems M=1 2446. 29 288. 07 -534. 64 -24970. 0 24. 723 1. 1951 Combustion Product MOLE FRACTIONS Burner M=1 Ar CO CO 2 H H 2 O NO N 2 O OH O 2 0. 00564 0. 00005 0. 00012 0. 00205 0. 01718 0. 29080 0. 00402 0. 66569 0. 00065 0. 00936 0. 00445 0. 00567 0. 00003 0. 00014 0. 00086 0. 01062 0. 30174 0. 00229 0. 67022 0. 00025 0. 00523 0. 00296

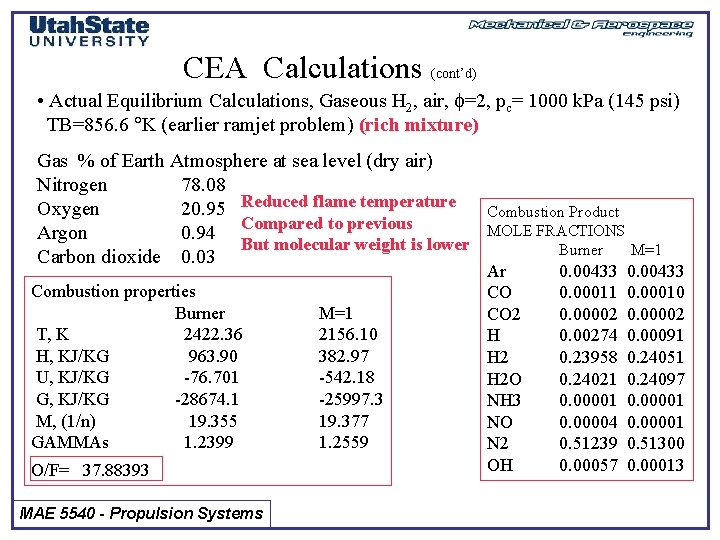
CEA Calculations (cont’d) • Actual Equilibrium Calculations, Gaseous H 2, air, f=2, pc= 1000 k. Pa (145 psi) TB=856. 6 K (earlier ramjet problem) (rich mixture) Gas % of Earth Atmosphere at sea level (dry air) Nitrogen 78. 08 Oxygen 20. 95 Reduced flame temperature Compared to previous Argon 0. 94 But molecular weight is lower Carbon dioxide 0. 03 Combustion properties Burner T, K 2422. 36 H, KJ/KG 963. 90 U, KJ/KG -76. 701 G, KJ/KG -28674. 1 M, (1/n) 19. 355 GAMMAs 1. 2399 O/F= 37. 88393 MAE 5540 - Propulsion Systems M=1 2156. 10 382. 97 -542. 18 -25997. 3 19. 377 1. 2559 Combustion Product MOLE FRACTIONS Burner M=1 Ar CO CO 2 H H 2 O NH 3 NO N 2 OH 0. 00433 0. 00011 0. 00002 0. 00274 0. 23958 0. 24021 0. 00004 0. 51239 0. 00057 0. 00433 0. 00010 0. 00002 0. 00091 0. 24051 0. 24097 0. 00001 0. 51300 0. 00013

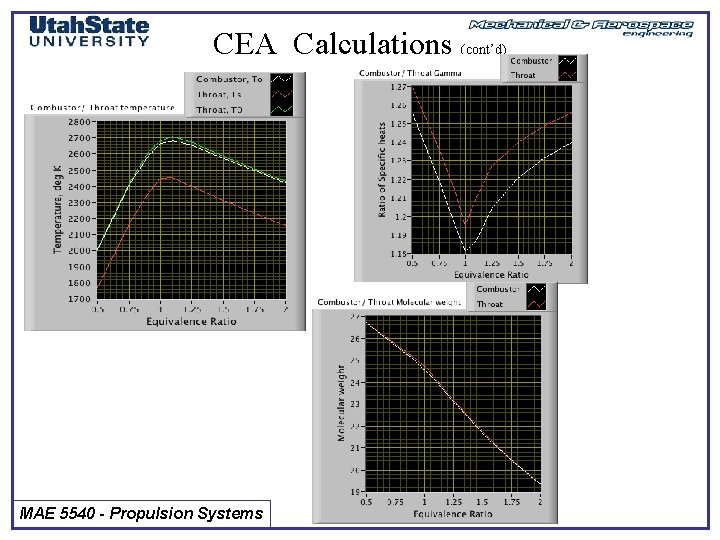
CEA Calculations (cont’d) MAE 5540 - Propulsion Systems

Specific Thrust of Air Breathing Engine • Analogous to specific impulse Cruise design condition When pe=p MAE 5540 - Propulsion Systems

Specific Thrust of Air Breathing Engine (cont’d) • Re writing in terms of mach number MAE 5540 - Propulsion Systems

Specific Thrust of Air Breathing Engine (cont’d) • Re writing in terms of mach number Function of Nozzle geometry Function of combustion MAE 5540 - Propulsion Systems f= F fstoich • Equivalence ratio, engine pressure ratio, nozzle drive process

Revisit Earlier Ramjet problem M 1=4. 0 b= 40 • Compute Specific Thrust for F=1, gaseous H 2 fuel • Nozzle Optimized for operation at ~10 km altitude (p =pe= 26. 43 k. Pa) …pburner ~ 1015. 5 k. Pa • Assume frozen chemistry at burner MAE 5540 - Propulsion Systems

Revisit Earlier Ramjet problem (cont’d) M 1=4. 0 b= 40 = 1253 k. Pa • Calculate exit stagnation pressure: = 4008. 5 kpa = 1253. 0 k. Pa MAE 5540 - Propulsion Systems

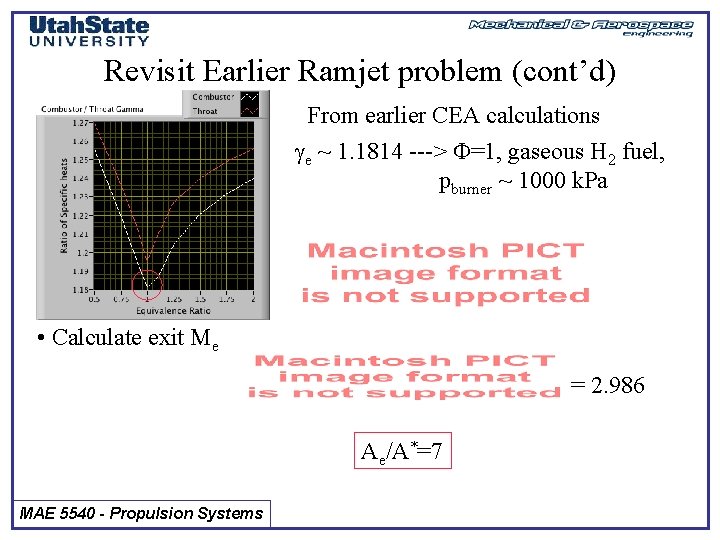
Revisit Earlier Ramjet problem (cont’d) From earlier CEA calculations e ~ 1. 1814 ---> F=1, gaseous H 2 fuel, pburner ~ 1000 k. Pa • Calculate exit Me = 2. 986 Ae/A*=7 MAE 5540 - Propulsion Systems

Revisit Earlier Ramjet problem M 1=4. 0 (cont’d) b= 40 • Assume Ae/A* = 2. 0 • Compute free stream stagnation temperature =909. 93 K MAE 5540 - Propulsion Systems

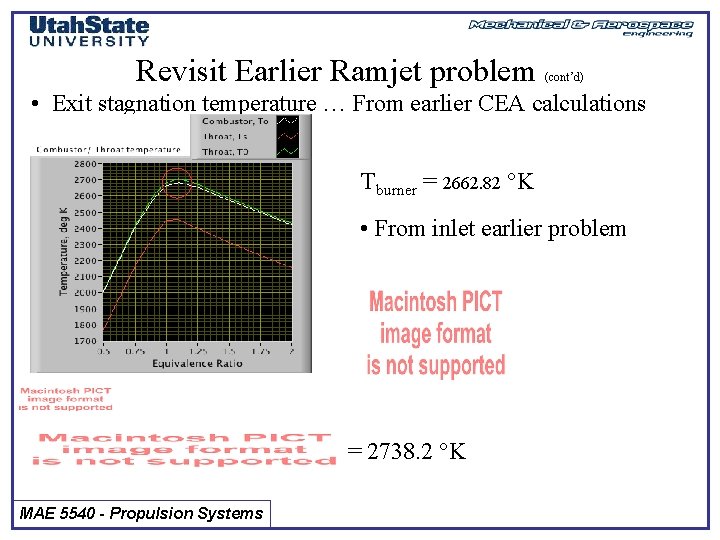
Revisit Earlier Ramjet problem (cont’d) • Exit stagnation temperature … From earlier CEA calculations Tburner = 2662. 82 K • From inlet earlier problem = 2738. 2 K MAE 5540 - Propulsion Systems

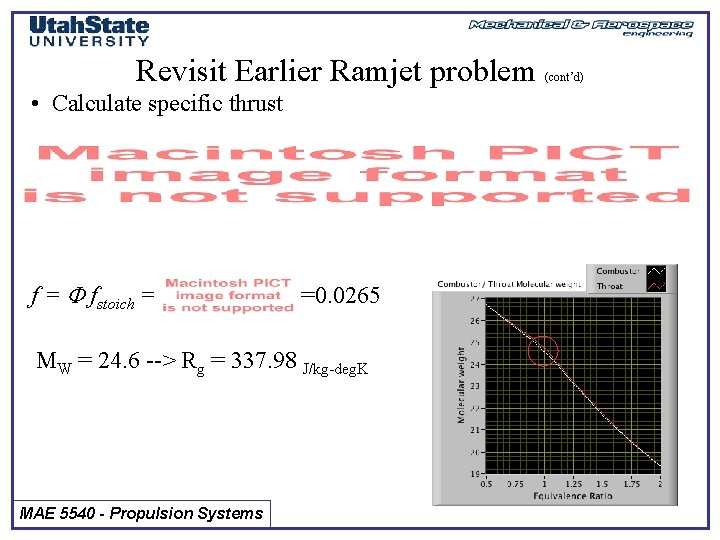
Revisit Earlier Ramjet problem • Calculate specific thrust f = F fstoich = =0. 0265 MW = 24. 6 --> Rg = 337. 98 J/kg-deg. K MAE 5540 - Propulsion Systems (cont’d)

Revisit Earlier Ramjet problem (cont’d) • Calculate specific thrust - = 45397 Nt/kg/sec … convert to seconds MAE 5540 - Propulsion Systems = 4628. 4 sec

Revisit Earlier Ramjet problem • Calculate specific thrust 4628. 4 sec MAE 5540 - Propulsion Systems (cont’d) • Idealized analysis … with a 2 -D inlet • If we consider losses of 10% then we are right in the middle of the predicted operating range

• Now one can see why air breathing options are so attractive Isp > 4000! …. Off the chart MAE 5540 - Propulsion Systems

What is thermodynamic efficiency = = 0. 600 MAE 5540 - Propulsion Systems

What is thermodynamic efficiency (cont’d) • Unlike Rockets. . Ramjets … and air breathing propulsion systems in general tend to run more thermodynamically efficient when the mixture ratio of leaner than stoich • Combustion efficiency and stability limits are depending on several parameters : fuel, equivalence ratio, air stagnation pressure and temperature • Airbreathers tend to run lean … that is why afterburners work … left over O 2 MAE 5540 - Propulsion Systems

What is thermodynamic efficiency (cont’d) • Additional fuel is introduced into the hot exhaust and burned using excess O 2 from main combustion • The afterburner increases the temperature of the gas ahead of the nozzle Increases exit velocity • The result of this increase in temperature is an increase of about 40 percent in thrust at takeoff and a much larger percentage at high speeds. . But big loss in thrust to fuel consumption ratio MAE 5540 - Propulsion Systems

Thrust Specific Fuel Consumption Measure of fuel economy of An airbreathing engine MAE 5540 - Propulsion Systems

Next: Supersonic Combustion Ram. Jets (SCRAMjet) MAE 5540 - Propulsion Systems