Introduction to Graph Theory Vertices and Edges Networks

Introduction to Graph Theory Vertices and Edges: “Networks” Important in Computer Science, Electrical Eng. , Social Sciences… part of Data Structures Discrete Mathematics, Graphs and Algorithms, part of: Combinatorics Prof. Hassane Bouzahir (Just google my name) 1 ENSA Agadir, 2014

1. Graphs § Graph A graph G = (V, E, γ) consists of a finite set V of objects called vertices, a finite set E of objects called edges, and a function γ that assigns to each edge a subset {v, w}, where v and w are vertices (and may be the same). § End points If γ(e) = {v, w}, then vertices v and w are called the end points of e. 2 ENSA Agadir, 2014

1. Graphs § Example 1 & 2 Let V = {1, 2, 3, 4} and E = {e 1, e 2, e 3, e 4, e 5}. Let γ be defined by γ(e 1) = γ(e 5) = {1, 2}, γ(e 2) = {4, 3}, γ(e 3) = {1, 3}, γ(e 4) = {2, 4}. Then G = (V, E, γ) is a graph. Isomorphic Graphs 1 2 4 3 G 3 1 2 3 4 G 1 2 3 G ENSA Agadir, 2014 4

1. Graphs § Degree. The degree of a vertex is the number of edges having that vertex as an end point. To be precise: the degree of a vertex is the number of endpoints on that vertex, i. e. , if an edge is from a vertex to itself, we count it two times. § Loop. An edge is referred to as a loop if the edge is from a vertex to itself. Note: a loop contributes 2 to the degree of a vertex, since that vertex serves as both end points of the loop. § Isolated. A vertex with degree 0 is called an isolated vertex. 4 ENSA Agadir, 2014

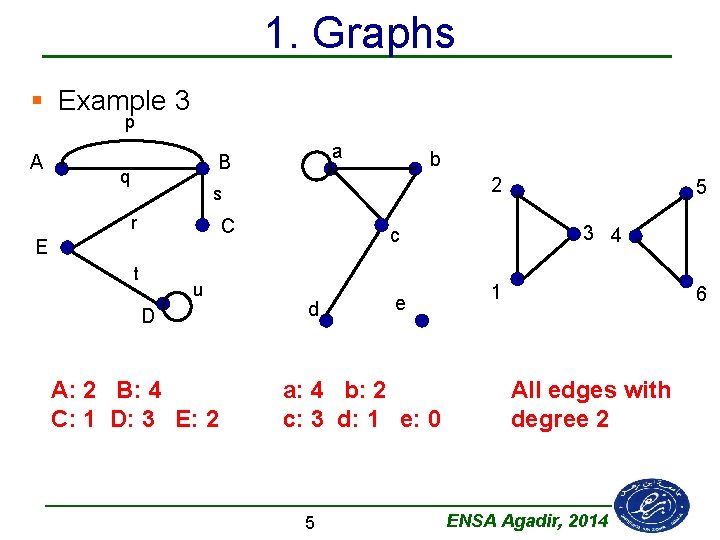
1. Graphs § Example 3 p A a B q b 2 s r C E t u D A: 2 B: 4 C: 1 D: 3 E: 2 3 4 c d e a: 4 b: 2 c: 3 d: 1 e: 0 5 5 1 6 All edges with degree 2 ENSA Agadir, 2014

1. Graphs § Path in a Graph A path п in a graph G consists of a pair (Vп, Eп) of sequences: a vertex sequence Vп : v 1, v 2, …, vk and an edge sequence E п : e 1, e 2, …, ek-1 for which 1. Each successive pair vi, vi+1 of vertices is adjacent in G, and edge ei has vi and vi+1 as end points for i=1, …, k-1; 2. No edge occurs more than once in the edge sequence. 6 ENSA Agadir, 2014

1. Graphs § Circuit (cycle) A circuit is a path that begins and ends at the same vertex. § Simple A path is called simple if no vertex appears more than once in the vertex sequence, except possibly if v 1= vk. In this case, the path is called a simple circuit. 7 ENSA Agadir, 2014

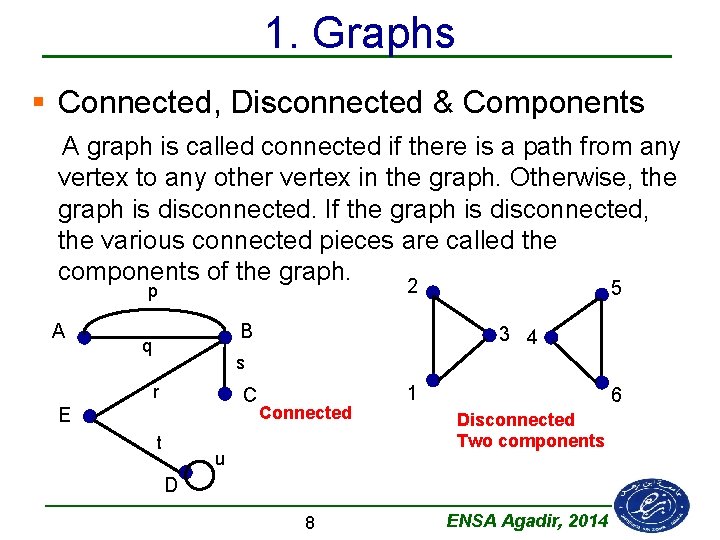
1. Graphs § Connected, Disconnected & Components A graph is called connected if there is a path from any vertex to any other vertex in the graph. Otherwise, the graph is disconnected. If the graph is disconnected, the various connected pieces are called the components of the graph. 2 p A B q 5 3 4 s r C E t Connected u 1 6 Disconnected Two components D 8 ENSA Agadir, 2014

1. Graphs Some important special families of graphs will be useful in our discussions. 1. Un (discrete graph) denote the graph with n vertices and no edges. U 2 U 5 2. Ln (linear graph) denote the graph with n vertices and with edges {vi, vi+1} for 1≤ i <n L 2 L 5 9 ENSA Agadir, 2014

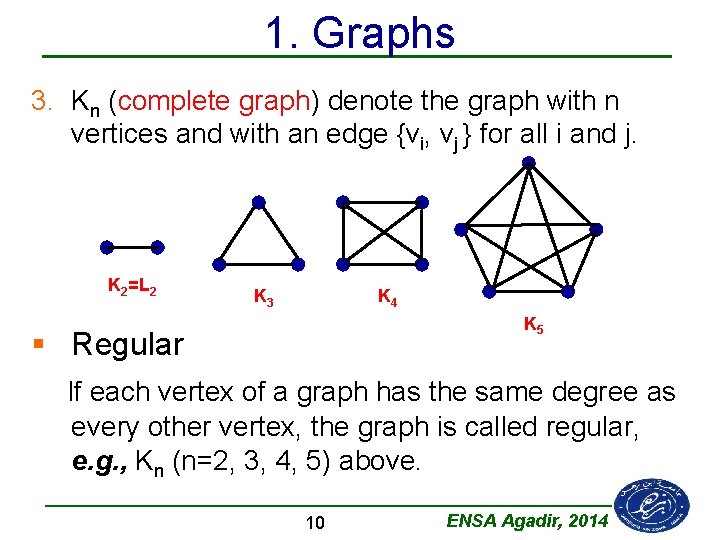
1. Graphs 3. Kn (complete graph) denote the graph with n vertices and with an edge {vi, vj } for all i and j. K 2=L 2 K 3 K 4 K 5 § Regular If each vertex of a graph has the same degree as every other vertex, the graph is called regular, e. g. , Kn (n=2, 3, 4, 5) above. 10 ENSA Agadir, 2014

1. Graphs § Subgraph Suppose that G = (V, E, γ) is a graph. Choose a subset E 1 of the edges in E and a subset V 1 of the vertices in V, so that V 1 contains (at least) all the end points of edges in E 1. Then H = (V 1, E 1, γ 1) is also a graph where γ 1 is γ restricted to edges in E 1. Such a graph H is called a subgraph of G. 11 ENSA Agadir, 2014

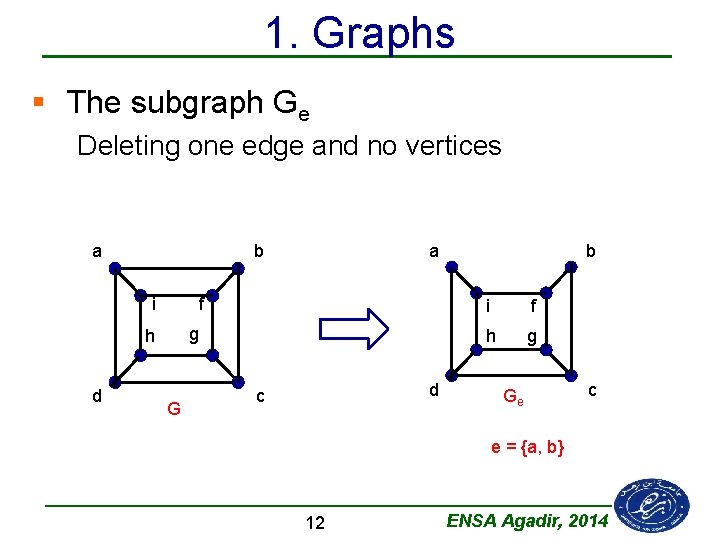
1. Graphs § The subgraph Ge Deleting one edge and no vertices a d b i f h g G a d c b i f h g Ge c e = {a, b} 12 ENSA Agadir, 2014

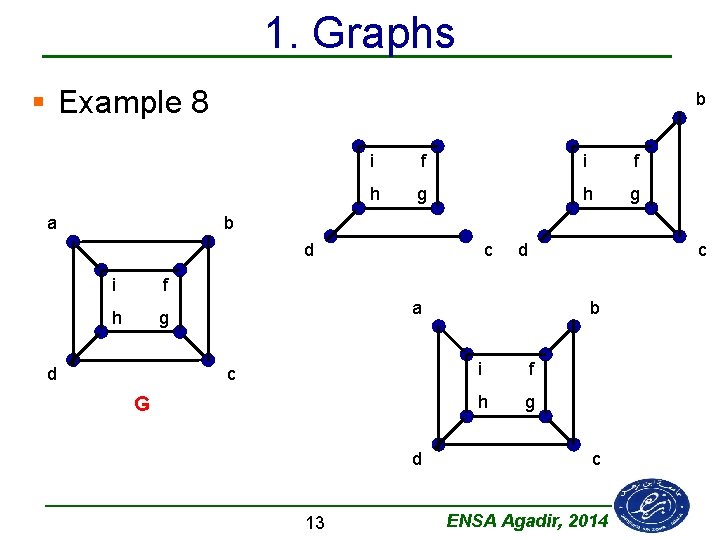
1. Graphs § Example 8 a b i f h g b d i f h g d c a c G d 13 b i f h g c ENSA Agadir, 2014

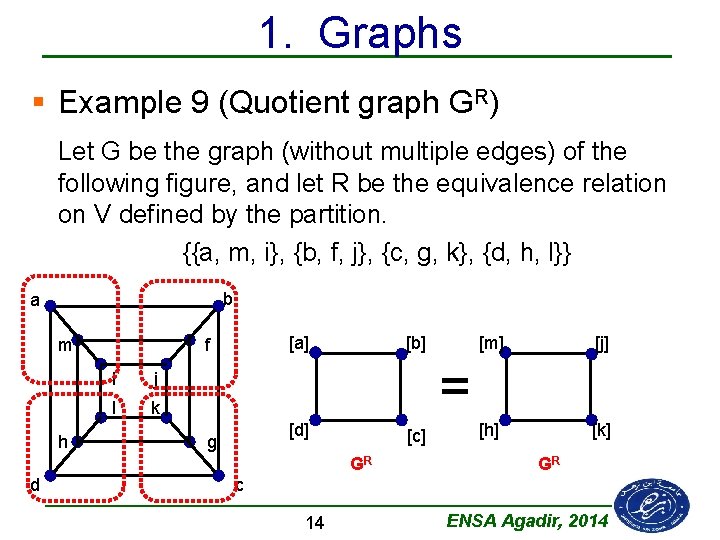
1. Graphs § Example 9 (Quotient graph GR) Let G be the graph (without multiple edges) of the following figure, and let R be the equivalence relation on V defined by the partition. {{a, m, i}, {b, f, j}, {c, g, k}, {d, h, l}} b a m h [a] f i j l k [b] [j] [h] [k] = [d] g [c] GR d [m] GR c 14 ENSA Agadir, 2014

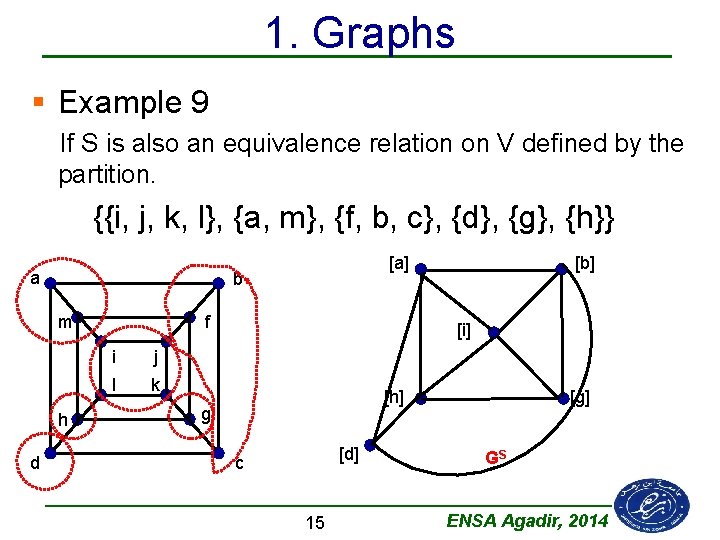
1. Graphs § Example 9 If S is also an equivalence relation on V defined by the partition. {{i, j, k, l}, {a, m}, {f, b, c}, {d}, {g}, {h}} a b m h d [a] f i j l k [b] [i] [h] g [d] c 15 [g] GS ENSA Agadir, 2014

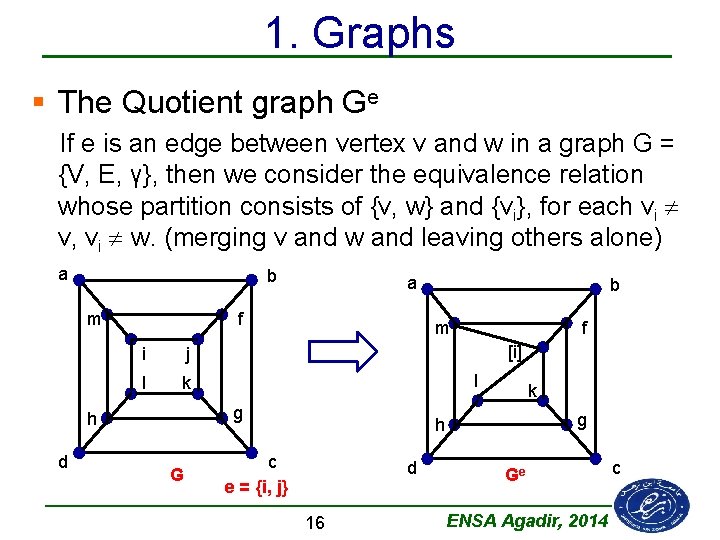
1. Graphs § The Quotient graph Ge If e is an edge between vertex v and w in a graph G = {V, E, γ}, then we consider the equivalence relation whose partition consists of {v, w} and {vi}, for each vi v, vi w. (merging v and w and leaving others alone) a b m f i j l k G b m f [i] l g h d a k g h c e = {i, j} d 16 Ge ENSA Agadir, 2014 c

1. Graphs § Homework Ex. 6, Ex. 16, Ex. 20, Ex. 22, Ex. 23, Ex. 29 17 ENSA Agadir, 2014